(2019年5月13日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > GIS回り
歴史1960年代: 基本構造できるがコンピュータ未普及1980年代: 欧米で発展 1990年代: 日本導入: ARC/INFO (ESRI社製) - GISスタンダード 1990年代: コンピュータハード・ソフトウェア進歩 → PC処理できる比較的安価なソフトウェア
デジタル地理情報整備 定義空間的な位置データを伴う情報をデータベース化し、検索、空間解析、表示などを行なう情報システム現実世界は、地形、河川、土地利用、行政界等複数カテゴリー要素から成り立ち、地形図でそれらを紙等の媒体に等高線や種々の記号で表現する。GISは個々の要素をコンピュータにデータ構造として格納しデータレイヤとして扱い、種々の解析表示を行なう情報システム |
位置情報 geometric information: 対象物に関する空間の位置や形状を示す
1. 入出力機能 |
(1) 位置情報表現モデル= 地図入力機能 map information input - 数値化ベクトルデータ vector formデータは座標と属性によって与えられる地物を「点」と「線分」と「面(領域)」とで扱い、それぞれに属性データを与え表現 = 各点を座標値として入力 → デジタイザー 地図情報をそのままコンピュータ上に表現する様式であり、正確に地理空間を表すことが可能で、特に、点や線分そして面の相対的位置関係である位相関係 topological relationship を表現できる利点をもつ
面 face: 植生・土地利用vegetation, landuse 利点データ構造が点、線、面を表現トポロジー的解析可能 面認識、接触関係、接続関係認識可能 データコンパクト 図形データ、属性データ検索更新容易 データ量が比較的小さい 位置情報精度がメッシュサイズに規定されない 位置情報正確 イメージデータより見かけ美しい 欠点[データ構造]ベクトル形式ポリゴンの正確な重ね合わせ困難 データ入力にスキャナ、プロッタ等の機器必要 データ構造複雑 → ソフト開発に高度技術必要 [空間解析] 複数ポリゴン図面での統計的比較等、 統計解析手法限定される ラスターデータ raster form= イメージデータ image data空間を規則的グリッドに分割し各グリッドに属性情報を付与し表現 データは2次元配列され、基本的に画像データと同形式で、コンピュータ処理が容易な利点をもつ。しかし、対象物を正確に表現するためにグリッドサイズを小さくするとデータ量が膨大になる Yes/No type, 階調(1-5, etc.) → スキャナー 利点
グリッドセル(メッシュ)大きさ一定___ 異なるデータ間でもオーバーレイ容易 データ入力に特別機器不要 ソフト開発容易 → 地図化容易 座標系でデータが与えられる 欠点[メッシュサイズ]
メッシュサイズ過小な場合 関心のある現象が抽出されない 地図表現の正確さを欠く 実質地域との整合性が確保できない |

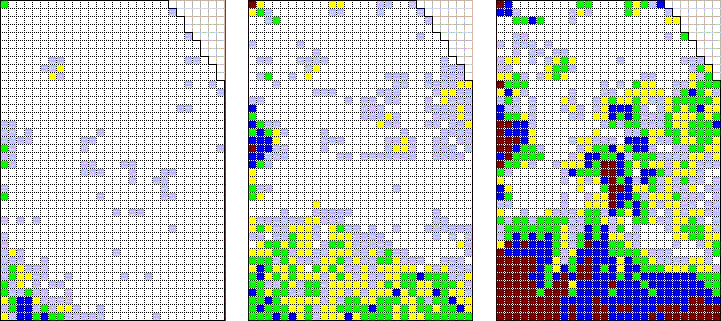 ラスターデータの基本構造 (赤い格子). 航空写真より得られた1963年(左)、1973年(中央)、1990年(右)におけるカラマツ(Larix kaempferi)の立木密度 衛星センサーによる記録はラスター形式である。 (2) ハンドリング機能handling地図属性(作成年)等の検索機能分布図・植生図等の作成や地形解析、さらに空間解析等を行なうツール面
植生図等の主題図作成 (3) 空間解析機能spatial analysisハンドリング機能踏まえ、モデリングやシミュレーション機能(情報システム面)
北大でのArcGIS利用方法包括契約ソフトユーザ申請システムから申し込めばよい。WebGISインターネットとGISが融合 → GPS搭載携帯型端末用い、現場でデータ閲覧し入力可能利用者は特別なソフト不要 → インターネット接続環境とブラウザさえあればGIS利用可 [方式]
GIS ソフトウェア (GIS software)水文水質データベース (国土交通省), 気象庁 (Tenki.jp (日本気象協会), 国土情報ウェブマッピングシステム村山祐司のホームページ, オープンソースを使う、GIS入門, BioEoS: 環境解析学研究室 |
|
環境資源情報を正確に素早く抽出するシステム
地質図・地形分布図・土壌図・植生図
→ オーバーレイ (McHarg 1969)
分布パターン(Turner et al. 1991) |
SFM= structure from motion複視点の画像から3Dを再現する手法
複数のカメラ、焦点距離で撮影されたものでも使用できる 森林GIS= 森林に用いるGISEx. 森林基本図、森林計画図、森林簿等の一元管理 |
|
(s.l.) 離れた点から直接触れず対象物性状を計測する技術 (s.s, 一般) プラットフォーム搭載センサを用い、地表からの反射・放射電磁波測定し、地表の物体・性状把握技術
プラットフォーム platform: 人工衛星(e.g., NOAA)や飛行機等のセンサ搭載部 仮定(成立しないこともある): 物体の種類・環境条件異なる → 異なる電磁波反射特性
→ 電磁波観測で物体識別や環境条件を把握 原理 principles多重スペクトル走査放射計(マルチスペクトルスキャナ multispectral scanner, MSS): 線走査データを可視光-遠赤外までをバンド分け → 信号を画像収録(= 光学センサ)
センサのデジタル値を較正(calibration)し放射量計算補正 + グランドトゥルース
グランドトゥルース ground truth: 地上実測値 → 教師付き分類 → 教師無し分類 ⇓ [影響因子] 太陽位置/大気状態・気象/季節/地表状態/センサ性能・位置 ⇓ [センサのデータ収集] 画像データ ⇓ [データ処理] 前処理/補正/パターン認識/分類 ⇓ [応用] 判読/解析/評価 図. リモートセンシングによるデータ収集 観測幾何 sun-target-sensor geometry地表面撮影時の太陽・観測対象・センサの位置関係 - 補正が必要(人工)衛星リモートセンシング利点: 広域データ瞬時把握 + デジタルデータ → 解析が容易・迅速
1972: 地球観測衛星 LANDSAT (当時ERTS) (米)打上成功 → 衛星リモセン普及 RBV (return beam vidicon)撮像管による高解像度画像とMSS4-7画像取得
センサ技術進歩: 空間分解能 resolution (地上解像度)向上や取得可能波長域改善 Ex. 合成開口レーダ センサー特性観測技術進歩に伴い空間分解能向上、観測波長域増大、時間分解能向上 → 地上データとの検証に関する研究進む → 解析困難だった生態現象や環境条件計測可能 → 画像特性
パンクロマティック panchromatic 画像: シングルバンド/モノクロ画像 |
放射波: 地表から自然に出てくる波 - 多衛星センサーが利用 反射波: ある波長を地表に照射し受け取る波 合成開口レーダ (synthetic aperture radar, SAR): マイクロ波地表照射 → 反射波受信 原理 反射波の振幅と位相を観測 (↔ 一般レーダ: 反射波強度のみ測定)
同一地域を時間を変え観測 → 地表面変化計測
→ 開口面を合成したレーダーが名称語源 宇宙からの合成開口レーダ観測は、1978年米国海洋観測衛星SEASATで始まり、日本の地球資源衛星1号(JERS-1)や、ヨーロッパ宇宙機関ERS-1、ERS-2、カナダRADARSAT衛星等で行われる。日本では、通信総合研究所(CRL)や国土地理院等が、航空機搭載合成開口レーダ観測を行っている
対象物: 波長 → 電波
→ Lバンド: 熱帯林、北方林等植生分布特定 → 植生変化(Ex. 森林伐採・火災)へ応用
目的にあわせた波長のSARを航空機・人工衛星に搭載 - 地球全体観測 今までのセンサでとらえられなかった詳細な解析が可能なはず ライダー LIDAR |
静止衛星 geostationary satellite赤道上で地球自転角速度と同じ角速度・向きで地球を回る = 地上からは静止Ex. ひまわり: 高さ35800 km、直下点を中心とする半径約6000kmの範囲の雲観測 極軌道気象衛星 Ex. NOAA(米), METEOR(旧ソ): 極地方 → 静止衛星から見えない緯度80°上 → 軌道両側±1500 km幅を12時間間隔で観測(極点カバー) 静止軌道衛星 geosynchronous orbiter, geosynchronous satellite静止気象衛星GSM極軌道衛星polar orbit satellite, polar orbiter, POES 可視赤外線観測衛星 TIROS → 主な地球観測・気象衛星の光学センサ等性能の比較 宇宙航空研究開発機構 (JAXA)元宇宙開発事業団(かつ元NASDA)所有の地球観測衛星データ (Table参)Satellite: Remote sensor JERS-1: SAR, OPS Landsat: TM, MSS SPT: HRV MOS-1, MOS-1b: MESSR, VTIR, MSR ERS-1: AMI/SAR mode ADEOS (Advanced Earth Observation Satellite, 1996 一号機) ADEOS II (みどりII): AMSR, GLI 2002 環境観測技術 → 積雪・土壌水分・海氷分布・水蒸気・降水量・海面温度・海上風・クロロフィル分布(AMSR, Advanced Microwave Scanning Radiometer: 自然放射微弱マイクロ波をマルチバンド受信し、昼夜別なく、雲有無によらず観測可能センサ) 改良型AMSR-EもNASA衛星Aquaに搭載され2002.5↑ |
WINDS きずな: 超高速インターネット 2008/2/3 17:55↑ 静止衛星軌道 軌道高度36000 km 軌道傾斜角0度 軌道周期24h GOSAT, いぶき: 温室効果ガス濃度を観測し大気異常を監視。2009年1月23日12:54打上 太陽同期準回帰軌道 軌道高度667 km 軌道傾斜角98° 軌道周期1h38m ALOS, だいち
PRISM (2.5 m, 可視光) GCOMGCOM-WGCOM-W1, しずく 気候変動観測: 海や陸の水の状態を観測し台風や集中豪雨を監視 2012.5.18 01:39↑ 太陽同期準回帰軌道 軌道高度700 km 軌道傾斜角98° 軌道周期1h38mマイクロ波放射計 (AMSR2): 降水量・水蒸気量・風速・水温・土壌水分量・積雪深等の測定を期待 GCOM-CGCOM-C1 気候変動観測: 塵・雲の分布調べ、火山噴煙や森林火災を観測 2016年予定。太陽同期準回帰軌道。軌道高度798 km。軌道傾斜角99°。軌道周期1h38m
多波長光学放射計 (SLGI): 380 nm - 12000 nm (解像度250-1000 m) → 雲・アエロゾル・海色・植生・雪氷等の測定期待 価格表 (SED)ALOS, COSMO-SkyMed, GeoEye-1/IKONOS, Quickbird, RapidEye, SPOT, WorldView-1, WorldView-2, WorldView-3, SkySat |
正規化植生指数 (NDVI)植物体の光学反射特性利用 → 近赤外と可視光(赤色域)の波長帯使用→ バイオマス・植生活性度等測定 NOAA衛星AVHRR: NDVIとLAI、光合成有効放射吸収量(absorbed photosynthetically active radiation, APAR)との相互関係に関する研究進み、グローバルな純生産量(NPP)推定行われる。技術はMODISに引き継がれた。AVHRR/MODISデータでは、時間分解能高く多時期データmulti-temporal data取得可能で、季節的変化を利用した植生分類や土地被覆分類できる 季節の異なるNOAA/AVHRRデータ → 植生型・土地被覆分類に有効な波長
改良植生指数 enhanced vegetation index, EVINDVI: 大気状態(Ex. エアロゾル - 散乱)影響EVI = G·(IR - R)/(IR + C1·R - C2·Blue + L)
L: 土壌影響補正係数 (Huete et al. 1994, 1997) |
正規化水指数 normalized difference water index, NDWI湿原等ではNDVIのみでの植生区分は不十分 → 水考慮値高い → (必ずではないが)表面帯水状態
= (赤 - 短波長赤外)/(赤 + 短波長赤外) (McFeeters 1996) 正規化土壌指数 normalized difference soil index, NDSILANDSAT-TM: NDSI = (TM5 - TM4)/(TM5 + TM4) (Rogers 2001) 土壌調整植生指数 soil-adjusted vegetation index, SAVINDVI: 非植生(Ex. 土壌)反射成分影響 - 低植生(Ex. 砂漠、草原)で精度低下SAVI = (IR - R)/(IR + R + L) × (1 - L) L: 土壌調整ファクター (0.5とすること多) (Huete 1988) 可視大気抵抗指数 visible atmospherically resistant index, VARI可視光のみ使用 = 画像データ(RGB)から計算可能 → ドローン等に利用= (green - red)/(green + red - blue) |
|
写真測量: 航空写真により被写体の情報を得ること (s.l.)
写真測量(s.s.): 位置、形態等測定 生態学における航空写真の有効性航空写真判読は、飛行高度によるが高精度で地表面情報を読み取れるリモートセンシング技術(remote sensing, リモセン, RS)である。例えば、駒ケ岳南西斜面では、カラマツが1本1本がはっきりと読みとれる。これを用い、複数年の航空写真を重ね合わせ、カラマツ本数の時間的変化が計れるRSは、衛星データが主流となりつつあるが、衛星稼動以前のデータは航空写真しかなく(それより古ければ写真もない)、まだまだ使いようでは様々な解析に用いられる 航空写真 → (地図化) → 林業経営資料 + 林相、樹種、地質、土壌等判定、森林資源現況把握等利用
森林航測空から森林の質量情報取得 (立体視)連続撮影 - 面積・樹種・樹高等測定 空中写真 = 航空 + 衛星 + 気球等 航空写真判読陸地測量部: 陸軍参謀本部外局で国内外地形等測量・管理等
国土地理院前身の1つ その後 → 山地部 = 林野庁 vs 平地部 = 国土地理院 林野庁: 普通角レンズ持つ航測用カメラ5年毎。撮影縮尺1/16000 国土地理院: 広角レンズ持つ航測用カメラ
写真重複度: オーバーラップ60%、サイドラップ30% 標定図: 林野庁は高度3400 mで概ね2 km四方写る エアフォームパターン airform pattern: ある高度で撮影した写真に現れる形状配置パターン
地形特徴や位置関係の傾向をよく示す → 航空写真判読で利用 航空写真: 周辺湿地林や泥炭地(muskeg)と明瞭な対比示す 慣性計測ユニット(GPS/IMUデジタル航測): 実体鏡不要
写真立体視はデジタル3D機器使用 - 3Dモニタ/ソフトウェア/偏光眼鏡 2008/11/12現在. 2013/02/04挙動確認 入手方法 (赤坂フォーマット改)
|
ドローン (drone, UAV)(簡単に)行けない場所に入れる Ex. 崖・沼地(簡単に)登れない場所に登れる Ex. 樹冠・林冠・鉄塔
リアルタイム
無人航空機(ドローン・ラジコン機等)の定義及び無人航空機飛行ルール 国重要施設(内閣総理大臣官邸等)、外国公館や原子力事業所等の周辺地域上空での飛行禁止 立体視 stereoscopic visionアナグリフ(余色写真): 赤・青2色で示した画像 - 赤青メガネ立体鏡 stereoscope簡易実体鏡(ステレオビュアー): まさに簡易版(ざっと見なら悪くない)反射式実体鏡 = 本体 + 双眼鏡 + 視差測定桿(マイクロメータ) 主点: 写真中心 = 対辺結ぶ線と線との交点移写点: 1枚目の主点に相当する2枚目の点 [立体視手順]
本数 = 樹冠(クローネ)カウント 樹種 = 樹冠サイズ・形・色等 樹高 = 立体写真法の視差測定桿で測る 樹高測定
h = (H/b) × p
h: 樹高 電子立体視鏡3Dグラスによる立体視「StereoViewerPro」 「もりったい」: 森林立体視ソフトウェア(販売終了) |
[統計学]
|
= 地球統計学 = 空間統計 spatial statistics → 空間解析spatial analysis (Tobler 1972) 地理学の第1原理全てのものは他のものと関係 → 近いもののほうが遠くのものより強く関係→ そのようなパターンは外因性 exogenous or induced・内因性 endogenous or inherentプロセスが混合し生じる 空間(R2, R3)中に生起するランダム現象統計解析
Def. 範囲 extent: 解析に用いる(のに適切な)空間範囲 ↔
ランダム現象 + 生起時間 → 時系列 → モデルの種類
データ分類Def. 定常性(移動不変) stationarity: 与えたn点の相互位置関係は他に移動しても不変 → 空間分析の仮定
強定常性 > 弱定常性 1. 確率場データ geoStatistical data観測地点(一般に連続空間上点)固定 – 空間回帰モデルを当てはめデータEx. 測候所降雨記録、観測地点汚染物質濃度、河川流域サンプル地点土壌浸透率(離散データ)
小規模変動: 観測地点距離が近ければ観測値も類似する性質でGeoStatisticalデータで見られる 2. 格子データ lattice data(不)規則的配置された領域の集まりに付随する観測値で、一般に「近傍情報」利用可能確率場データと点パターンデータの中間的位置づけ Ex. 規則的格子: リモートセンシングデータ(R2規則的格子)、不規則格子: 州内各郡癌発生率 Def. 格子 lattice (数学): 頂点vertexと辺edgeからなる構造
– 格子データ: 各サイト = 頂点、近傍同士 = 辺が辺で結ばれる Ex. 共有する州境の長さに比例させた重み Ex. 距離や共有境界長を元にした近傍定義や最近接距離算出, 空間的自己相関算出検定, 共分散構造に条件付自己回帰(CAR)モデル, 同時自己回帰(SAR)モデル、移動平均モデルを仮定した空間回帰 3. 空間点パターン spatial point patterns点パターンモデルを当てはめるデータランダム性検証 randomization test → H0: CSR (complete spatial rondomness)
Kernel, Loess, Gaussianモデルによる強度推定
2 種の点が離散(集合)する空間スケールを得る 空間(的)自己相関分析オブジェクトの位置と属性を同時に考える → 点パターン分析では不十分Def. 空間自己相関 spatial autocorrelation, ac (Cliff & Ord 1981, Haining 1990)
存在確認(検定)法 [仮定 m, s一定]
→ [適用に制限] 正方形セルのラスタデータ + 2値属性 binary
|
方法: 全隣接(上下左右)セル対のうち白黒対を数える(N) N↑: 正ac > ランダム分布: E[N] = 75.40 > N↓: 負ac 検定 → H0: 特定傾向存在しない = 白黒はランダム分布 領域内の白(w)黒(b)数、領域縦(c)横(r)セル数 ランダム分布N期待値, E(N) = 2bw(2cr – c – r)/{cr(cr – 1)} N < E(N) → 正の空間的自己相関 N > E(N) → 負 統計的検定(セル数十分なら検定可能) → 白黒がランダムに割り当てられる場合Nは V(N) = bwS1/{4cr(cr – 1)}
+ bw(S02 + 2S0 ~ N(μ, σ) [S0 = 2(2cr – c – r), S1 = 8(8cr – 7c + 7r + 4)] → 統計量 z = (|N – E(N)| –0.5)/{cr(cr – 1)},
0.5はNが整数値しか取らないことを考慮した調整用の値 Join統計量は、隣接関係を上下左右4方向ではなく、斜めを加え8方向にしても、ほぼ同様に用いられる [応用(多値属性を持つ場合)] コンビニエンスストアの競合関係
統計的検定 → モンテカルロシミュレーション 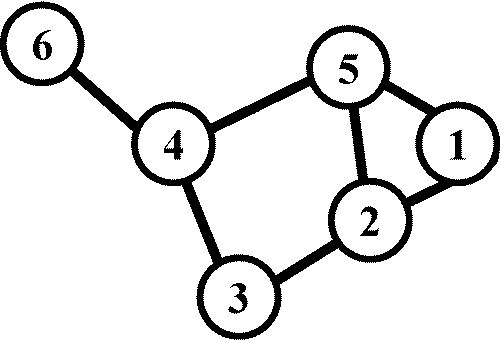 隣接行列 neighboring matrix, adjacency matrix: グラフを表現するために用いる行列
隣接行列 neighboring matrix, adjacency matrix: グラフを表現するために用いる行列
頂点vとw間の枝の本数を行列の(v, w)成分に割り当てる ↔ 枝がないとき(v, w) = 0 有向グラフ → vからwに向かう枝があるときのみ(v, w) = 1 ↔ そうでないとき(v, w) = 0 枝に重みがつくグラフ → (v, w) に重みを代入 Ex. 6ノードと 7のエッジから成るグラフとその隣接行列
均質性仮定 + Join統計量 問題点解決 Moran's I = n/A·Σi,jWi, jzizjΣizi2
オブジェクト属性とオブジェクト間近接性が定義された対象ならよく"点-線-面"データに適用可能 Ex. 近接性Aij及び領域間距離dij: 重心間距離の逆数 最短距離。ネットワーク距離。時間距離 Moran's Iの統計的検定: 各領域に属性値をランダムに割り当てる状態で期待値E(I), 分散V(I)を考えるE(I) = –1/(n – 1) V(I) = {(n2 – 3n + 3)/S1 – nS2 + 3S02 - Σi(x – m)4/{Σi(x – m)2}2·(n(n – 1)S1 – 2nS2 + 6S02)}/{(n – 1)(n – 2)} I ≈ N(E(I), V(I)) → Moran's Iは近似的に正規分布に従う → 統計的検定可能Moran's I注意点: 近接度を表す変数設定が重要 (df大な分、分析対象に適した変数を選ぶのが難しい) b) 局所的空間自己相関 local spatial autocorrelationLocal Moran's I 2. 他の空間パターン解析指数
Pielou, Pi |
|
(Matheron 1963) バリオグラム (variogram)空間的相関、データのもつ距離と方向に関する関係を評価[仮定] 本質的定常性成立 [手順] バリオグラムクラウド → 経験バリオグラム → 理論バリオグラム 0. バリオグラムクラウド variogram cloud, VC対をなす標本間(ua, ub)の非類似度(γab)を特性値(z(ua), z(ub))を用い距離に対してプロット
γab = (z(ua) – z(ub))2/2 1. 経験バリオグラム empirical variogram値得られない位置値をクリギング点推定 → 分散構造予測 → 一般化クリギング(トレンド推定)γ(h) ≡ (1/2|N(h)|)·ΣN(h)(zi – zj)2 → Def. 2γ(h) ≡ バリアンス variance a. Def. セミバリアンス semivariance,
全方向バリオグラム: 全方向を考慮
(セミ)バリオグラム (semi-)variogram: (セミ)バリアンスをプロット – 混同されるが、通常バリオグラムと呼ぶ
ナゲット nugget = γ(0): 小スケールの変動、測定誤差
hをどう選ぶか N(h) ≥ 30のhに対し行う。γ(h)値に信頼を持てるのはDを2点の最大距離とするとh < D/2 の範囲のみ 一方向バリオグラム directional variogram: 北から時計回りの角度を指定した一方向のみのバリオグラムb. コバリオグラムcovariogram, C(h) = cov(z(i + h), z(i)), for all i, i + h ∈ D c. コレログラム(自己相関関数) correlogram: ρ(h) = C(h)/C(0) = 1 – γ(h) バリオグラム頑健推定 (Cressie & Hawkins 1980), 統計量 γ(h)
= {(1/2(h))·ΣN(h)(zi – zj)1/2}4/(0.457 + 0.494N(h)) 2. 理論バリオグラム[仮定] 等方向: バリオグラムが距離のみの関数クリギング kriging既知部分, U = {u1, u2, …, un}→ Z(U) = {Z(u1), Z(u2), …, Z(un)} → Z*(u)を推定 単純クリギング simple kriging, SK特性値とその平均からZ*(u)を推定 → OK, UK, CKはSKの改良版
理論バリオグラムでナゲット効果モデルを取り入れたもの u, ua: 位置, Z(u): 位置uでの確率変数, m(u) = E(Z(u)): 確率変数Z(u)の位置に依存する期待値
l: 重み(荷重) = Σb=1nλb(SK)C(ub, ua) = C(u, ua), a = 1, 2, …, n Σb=1nλb(SK)C(ub – ua) = C(u – ua) 通常クリギング ordinary kriging, OK理論バリオグラムのうち、ナゲット効果モデル以外のモデルを取り入れたもの
Z*OK(u) = Σa=1nλa(OK)(u)Z(ua) 普遍クリギング universal kriging, UKZ(u) = m(u) + R(u), m(u): 傾向変動(トレンド), R(u): 残差
m(u) = Σk=1Kakfk(u) λ = Σb=1nlb(UK)(u)C(ub – ua) + Σk=0Kμk(u)fk(ua) = CR(u – ua) コクリギング co-kriging, CK: 荷重(λ)の取り方でSCK, OCK, UCKが可能
U = {u1, u2, …, un} → Z(U) = {Z(u1), Z(u2), …, Z(un)}, → U, Vの2特性値から別な点WのZ*(w)を推定 Z*(CK)(u) = Σa1=1nλa1(u)Z(ua1) + Σa2=1ωa2(u)Y(va2) 非線形クリギング nonlinear kriging, NK: データを非線形変換解析 → 逆変換(値を元に戻す) 空間モデル (spatial model)空間操作・空間解析で得た空間パターンに基づき作られる空間現象記述数理的モデルEx. 空間回帰モデル・空間選択モデル・点パターン過程・空間拡散過程 空間モデルは、分野毎に開発が行われ一般化遅れた = 体系的説明困難 空間回帰モデル: 点・線・面の各オブジェクト付随属性記述モデル → 理論的(行動)モデルとは言い難いEx. 各空間集計単位での作物の単位面積当たり収量を各空間集計単位の気温・標高・雨量等で説明 領域 S{S1, S2, …, Sn},
領域iに与えられる被説明変数yiと説明変数xi1, xi2, …, xip
1) バリオグラムモデル
2) 空間誤差モデル spatial error model, SEM誤差分布の分散共分散は,空間的な距離の連続関数として表すことができる(距離のみに依存する)という仮定をおかないモデル3) 一般化線形モデル generalized linear model4) Geographically Weighted Regression Model (GER)回帰式パラメータβが空間上の位置により異なることを明示的に組み込んだモデル5) Bidimensional Regression Model変数をベクトル表現 → 関係を線形式記述 (Ex. 地図歪み補正の1方法)
空間選択モデル空間におけるオブジェクト選択行動記述モデル(主に地理学で開発) Ex. 買物先・居住地・観光地・経路選択 h5>1) 重力モデル 領域間の移動交通量や通信量等の記述Newton重力モデル, yij = G·(Mm/dij2) → 重力モデルから作成 領域 {S1, S2, …, Sn}, 領域iから領域jへの移動数, yij, 領域iとjの間の距離, dij yijはdijに明らかに影響を受ける。しかし,iからjへの移動は、他移動候補先1, 2, …, j - 1, j + 1, …, nまでの距離や各領域の持つ移動発生ポテンシャルを考慮し、以下のモデルを考える yij = αipβjqeγdij
αiは領域iの移動発生地としてのポテンシャル, bjは領域jの移動到着地としてのポテンシャル |
1)は重力モデル固有の問題で重要 → 各領域内の人口は既に与えられているにも関わらず、それ以上(以下)の移動数を予測してしまう可能性がある → 解決には、通常Poisson回帰モデルを適用 → 少なくとも問題点1-3は解決 + p = q = 1とし、その代わりにポテンシャルa1, a2, …, an, b1, b2, …, bnも同時に推定すれば問題点4も解決可能2) ハフモデル消費者店舗選択行動モデル – 実際の店舗選択データを用い、店舗選択行動を数理的に記述消費者{C1, C2, …, Cm}, 店舗{S1, S2, …, Sn} Sj 魅力度(Ex. 床面積) = Aj, CiがSjを選択する確率 = pij, CiとSjの(時間、直線)距離 = dij
pij = (Aj/dijλ)/(Σi=1n(Ak/dikλ)) 3) ロジットモデル logit modelハフモデル同様、多選択行動記述に用いるモデル。マーケティング・交通工学が発祥→ 適用範囲広範 = 統計ソフトパッケージ多(自作の必要性低い) 消費者{C1, C2, …, Cm}, 店舗{S1, S2, …, Sn}Sjの属性k(床面積, 価格等) = Ajk, CiがSjを選択する確率 = pij, CiとSjの(時間,直線)距離 = dij pij = exp(–αdij + ΣknβkAjk)/Σk=1nexp(–αdik + ΣlβlAkl) α及びβiが未知パラメータで、これらを実データから推測。いずれも距離や店舗面積等の要因が選択行動に与える影響の大きさ(重み付け)を表す [推定] 最尤法が用いられ、検定に尤度比検定を利用できる
選択肢集合の設定問題 Ex. 買物先 1)「池袋」選択,2) 中で「東武」を選択,3) 中で「レカン」を選択)という行動 選択行動は多段階であり、各段階にロジットモデル適用する必要生ずる。しかし、モデルを複雑化し、モデル推定精度低下(またはそれを防ぐためのより多くのデータ取得)を招き解決は容易ではない 4) 点パターン過程 point pattern process (stochastic point process)点パターン過程: 空間オブジェクト空間データ部分記述モデル↔ 空間回帰モデル、空間選択モデル: 空間オブジェクト付随属性説明モデル 点オブジェクト: 最も基本的な空間オブジェクト
点パターン過程は、植物や地震、疫病患者等の分布説明に用いられ、生態学で開発されたものが多い 有界な領域: S, 点の個数: n 点がランダム分布 → Sの部分領域sに含まれる点の個数p(s)が従う確率分布 P(p(s) = x) = (nCx/n!)·(A(s)/A(S))x·(1 – A(s)/A(S))n–x, A(S)はSの面積を表す関数 分布は二項分布 → この点パターン過程を二項点過程と呼ぶ点分布データ → 二項点過程当てはめ可能 未知パラメータn: 観測データにおける点の個数を推定値として用いる。即ち、モデル推定は自明 b) 一様Poisson過程 homogeneous Poisson process: 有界領域を無限領域に拡張したものi) 任意の有界領域sにおける点の個数は平均λA(s)のPoisson分布に従う
どの領域をとってもその中に含まれる点の密度(≡ λ, 強度 intensity)は一定である どの領域をとってもその中に含まれる点の分布は独立に二項点過程、つまり、一様ランダム分布する 点分布データに対する一様Poisson過程の当てはめは二項点過程の場合ほど自明ではない → 通常、観測データ領域は有界 (↔ 一様Poisson過程の想定している無限領域ではない)。しかし、λ推定値としては、点の個数Mをデータ領域全体の面積Aで割った値を用いることが多いc) 非一様Poisson過程 (inhomogeneous Poisson process) 一様Poisson過程: λは場所によらず一様(仮定) → 仮定緩和しλを場所の関数λ(x) → 強度関数 ≡ λ(x)
i) 任意の有界領域sにおける点の個数は平均∫x∈Sλ(x)dxのPoisson分布に従う
1) ノンパラメトリック法
カーネル法は、本来、点分布からその従う確率分布を推定する方法
カーネル傾きパラメータ決定方法: 最小二乗相互評価法least-squares crossvalidation method → データ中1つを除いた時のカーネルを想定し、それが残りの一点をよく説明するようパラメータを定める 2) パラメトリック法
λ(x)が外的要因に定められると考え、想定外的要因関数形を与え、データに合うようパラメータ推定する
ランダム集合モデルrandom set model点でなくポリゴン変化過程の記述モデル Ex. 細胞成長モデル時点1での細胞, S1。時点2での細胞, S2, 成長素, Z
S2 = S1∪{∪Zi; i ∈ Ω}, Zi: 点iで定められる成長素, Ω: 1で与えられた点集合 ランダム集合モデルは空間モデル中では複雑だが、推定・検定は可能 マルコフ連鎖モデル Markov chain model土地利用変化等の時間的空間配置変化記述モデル2時点の土地変化から、土地利用遷移行列Mを計算し、それを用いて時点3以降の土地利用を予測 他モデル
空間伝播モデル 空間明示モデル spatially explicit model⇔ 空間不明時モデル spatially implicit model |
|
(淵上 1987) 自己相似性基本図形(ジェネレータ)の繰り返しにより形成される次元 dimension: フラクタル構造は非整数次元を持つ 空間充填曲線: 1次元曲線であるにも関わらず無限点において2次元平面を過不足なく埋めつくす曲線 Ex. Peano曲線、シェルピンスキー曲線 1次元とも2次元ともいえる曲線 → 自己相似性含む → 全点で微分可能 相似次元フラクタル次元表現 - 非整数次元定義必要 (Hausdorff & Besikovic 1937)線分[0, 1]をN等分するとN個の部分に分かれ1/Nの線分がN本集まり全体を構成する。正方形は一辺が1/Nの正方形がN2個集まり全体構成、立方体はN3個集まり全体構成し、Nnの指数部分(n)が各図形の次元となる。故に、ある図形が全体を1/Nに縮小した図形P個で構成される時、P = ND → D = logP/logN (D = constant)で表わされ、Dを相似(フラクタル)次元と呼ぶ Ex. 1. ペアノ曲線
全体を1/2(N = 2)に縮小した図形4個(P = 4)によって構成される Ex. 川本支流, 肺・血管構造、星分布, 幹枝 再帰図形 recursive figure円、三角形等のジェネレータを回転縮小しながら決められた図形上に配置シェルピンスキーのガスケット Sierpinski gasket
 セルオートマトン cellular automataある規則に従い自己増殖していく状態を示すもの位置 (i) 時間 (t) 1 2 3 4 5 6 7 8 9 格子の1マスをセルとし、1つ1つのセルが周囲の状態により決定される |
 5線分からなるG______コッホ曲線G________ドラゴン曲線G G: ジェネレーター セルの動きによって作り出される4パターン(Wolfram 2002)
Type 1. 時間発展と共にセル消滅 
コード変換: 周囲のセルから算出された値をあるコードで変換し新しいセルの値をすること 複素平面自己平方フラクタル: 有限空間上にf(z) = z2 + A (z: 複素変数, A: 複素定数)で与えられた図形発散点のみあるいは発散点と収束点からなる自己相似図形となる マンデルブロート集合: zn + 1 = fc(zn) → fc(z) = z2 + C
→ zの初期値を0とした漸化式
コンピュータ上での 空間データマイニング空間データ → 情報をPCで半自動的検出(PC性能向上 = 発展)Ex. 空間クラスタリング, 分類, 規則発見 |
[情報表現]
コンピュータグラフィックス (CG, computer graphics)
画像情報のデジタル情報化ピクセルで画像を描く原理画像image符号化は、まず画像全体を縦横に枡目分割する。原理は、マスゲームで人文字を描くのと同じで(図2.20)、A君が電話で離れた所にいるB君に模様を黒1色で描かせる様子を示す。A君B君は、同じ目盛の方眼紙を用意する。A君の目盛は透明プラスチック板、B君は普通紙とする
A君とB君の約束 1. A君が電話口で0か1という言葉を順にB君に伝える 2. B君は0が来たら白で1が来たら黒で桝目を塗り潰す 塗る桝目指定ルール(A/D変換)
1. A君が0か1を伝える順番は1行1列目から2列目...と最後の列まで行き、次に2行目に移る。以降、最終行まで繰り返す A君の色決めルール 1. 桝目の中心を選び(標本化)、白なら0黒なら1とする(量子化)
画像情報のデジタル情報化画像全体情報は、全ピクセル情報を合わせたもの。画像サイズは、縦横方向の枡目数を意味し「200 × 150 px」の様に表わす。このルールで画像を送ると黒1色のため色誤差(量子化誤差)はないが方眼が荒いとB君が作る図は元画像と異なる(標本誤差)。方眼を半分半分と細かくすると元絵に近づき、目には同じ様に見える様になるが、標本化を細かくすれば扱う0, 1量は急激に増え(今の場合2乗)、画質と扱うべき情報量の間にトレードオフがあるカラー画像 (color image)「色決めルール」部分が変わる。ただ、色は連続変化なため方眼の中心色を幾つかの色に量子化し使うため量子化誤差が入る。基本色RGB輝度用にNビット用意すると作成可能色は幾つか。N = 2の時の色種類(1 pxあたり2b × 3の6ビット仕様)(1)2ビットで出来るビットパターンは、00 01 10 11の4種類(22)(2)各ビットパターンを、輝度0(なし), 1, 2, 4(最高)と対応(3)ピクセルの色をC(R輝度, G, B)で表すとR輝度種数 × G数 × R数(= 4 × 4 × 4)の64色となるEx. 暗赤 = C(1,0,0), 明緑 = C(0,4,0), 明黄 = C(4,4,0), 黒 = C(0,0,0)
文字色の様に数色でよいなら、適当な長さのビット列に色を割当てる方法が使われ、4ビット16色もあるが、この方法で利用者が色を作ることはできない ビット浪費者としての画像処理実存色を本格的に使うフルカラーは、1 pxに8 bit × 3(1 byte × 3)かかる。640 × 480 PCで最も荒く1画面に画像を描くと92万byte (740万bit)必要である(3 bt × 640 × 480 = 921600 byte = 7372800 bit)。比較するとa) 1.44 Mbディスクで2画面保存困難。b) JIS漢字コードは1文字2 btで、480 × 640画像は41万文字に対応し400字原稿紙1万枚強。C) ISDN転送速度は64000 b/秒で1画面送信に144秒必要。テレビは30枚分/秒の画像で動画を作るのでISDNでテレビ電話は作れない。画質を落としても見られる写真画像を扱うには色用に16 bit (2バイト)必要となる。画像は莫大なビットを消費する。VOD, video on demandは、見たい時に見たいタイトルの映像情報を提供する機能及びサービスだが、高速回線開発が必要となる漢字やAlphabet文字も画面には24 × 24といったピクセルパターン表示される点は画像と同じ。ただし、文字処理は、予め個々の文字画像パターンをメモリ記憶させ文字コードだけで処理するため少ないビットで扱える。電報で「1011お願いします」で1011に用意してある文の結婚祝電報が打てるのと同じ xDSL, x Digital Subscriber Line: 既存通常電話回線を使用し、高速デジタルデータ伝送する技術の総称 利用者と、局の双方で専用モデムを利用し、8 Mbps程度の伝送速度を実現する。従来モデムは、4 KHz以下の周波数帯域を使用するのに対し40 KHz以上の高周波帯を使用することで高速伝送を行う
表. xDSLタイプ。伝送速度 = 「上り: 利用者 → 局/下り: 局 → 利用者」 画像加工コンピュータで画像加工が容易な最大の理由 = デジタル画像情報を数値処理色の置換 「部屋の壁紙を変えたいが、模様は良いが色に飽きた。カタログ見本は不安なので、いい方法を教えて欲しい」。この課題を解決せよ。
画像合成古いSF映画: 怪獣-背景合成部分明瞭 → デジタル画像: 合成部分不明瞭Ex. 天気予報。テレビカメラをA, B 2台用意し、Aは天気図を、Bは解説者を写すが壁は単色(青が多)にする。2台のカメラで写された映像はA/D変換しコンピュータに送る。コンピュータは、入力されたBのある座標のデジタル画像情報が単色に当たる2進法数値の場合、同座標に当たるAの数値を出力し、単色以外(解説者)の数値の場合はそれを出力する。出力数値はD/A変換しアナログ情報に戻しテレビ電波として発進する。このようにし全座標色データを見ると天気図の前で解説者が説明する画面となる 画像変形写真をカットガラスごしに見ると変形して見えるのは、(A → B)の写像問題となる。図形は点集合で表せ、A(x, y) → B(s, t)対応関係を示す式を作る問題となる。この関数が分かれば、デジカメ写真を変形しディスプレイに映し出せ、連続的に行なうとSF映画の様な画像となる。Ex. テレビコマーシャルテクスチャ・マッピングtexture mappingは、3次元(3D)グラフィックスで描画するオブジェクト表面に2次元の絵柄(テクスチャ)を貼り付けることをいい、物体表面の質感等を容易に表現できる。レンダリングrenderingは、3Dグラフィックスデータを2D画像に変換表示することで、座標変換や画素色の計算等を大量実行する必要がある |
画像情報圧縮描画ソフトペイント系描画ソフト: 画像を直接扱い絵具で絵を描くようなソフト Ex. MSPaint, Adobe Photopaint ↔ ドロー系 画像はピクセル毎に色情報を作るため情報量膨大となり、画像情報量圧縮(ビット数を減らす技術)が登場した(画像圧縮 compression)。圧縮方法まで含めた画像表現方式に規格がある(Ex. GIF, JPEG, TIFF)。絵画や写真といった画像はアナログ量で、デジタル変換する際に標本化と量子化を行なうが、この段階で既にアナログ情報を圧縮するが、なお画像情報量は莫大なため、デジタルの特徴を利用し更なる圧縮が必要 ドロー系描画ソフト: 図形の1種として文字や(小さな)画像を含め配置するソフト Ex. MSDraw, JustSystem花子 幾何学的図形等からなる図では、「どこに、どのような太さと色の線を引く」という情報を符号化し表す方が、一般に1. 画像より少ビット数, 2. 自由な大きさに拡大/縮小, 3. 変更容易、という点で優る。例えば、円を書き保存記録する場合、円中心座標・半径という形で扱うため記録情報容量少ない。図形を幾つかのパラメータで扱う点に着目した画像圧縮技術だが、写真や絵画など不定形構成要素から出来た画像は扱えない 画像情報圧縮静止画像圧縮: 普段目にする風景 = 青空に白雲 + 芝生上 + ピンクの服を着た人 → 同色や比較的似た色の広がりで構成 = 静止画像圧縮のポイント1) 同色の広がり。デジタル情報変換で「赤赤…赤赤」と同2進法値ビット列が続けば、A/D変換時にこの構造を「赤n個」と置き換え、少ビット数に画像情報圧縮できる。元画像色が単純なほど、圧縮率高い 2) 類似色の広がり。自然風景で同色に見える部分も機械測定では異なるが、ヒトは色彩判別能力(分解能)以下の色は同色と判断する。この原理は既に量子化誤差段階で使われ、基準は器具を使い濃淡異なるRGB各単色を測定するものにあたる。自然環境下で人間は機械的に一定分解能で判断していない。多くの人は、2人の人を真横に並べれば5 mmの身長差が分かっても、2 m離れると同じに見える。256段階で量子化した約1670万色デジタル画像を数万色に精度落としても気にならない。この人間認知特性(視覚特性)を利用し、類似色を同1色にまとめ圧縮する。これらを組合わせ画像情報量を小さくする GIF (Graphic interchange format): 色調256色以下に落とし(2)、同色情報配列を数値情報化し(1)圧縮し、画像劣化ない特徴 → 複雑な画像の圧縮率は低 JPG (Joint photograpic experts group): 1667万色以上扱える。人間の輝度変化に鋭いが色調変化に疎い特性を使い色情報を間引く。そのため、完全再現できず(不可逆圧縮)、圧縮率を高めるほど画像劣化する TIFF: Windowsメタファイル形式。Windows描画命令(GDI命令)をファイルにまとめたもの。プログラムであるため拡大縮小が自由自在な点が特徴。Aldus社とMicrosoft社によって開発されたビットマップファイル用のフォーマット。汎用性高く、はがきソフトなどの「素材」で使用されることがある 動画像圧縮: 動画は、音同様にサンプリングするが各サンプルは画像情報(フレーム)でフレーム数は10-20/秒が普通 → 動画情報はビット数多く圧縮必須 動画圧縮原理はアニメーションと同じで、アニメは24枚/秒必要だが全部描くと大変なので、静止背景を1枚描き、変化部分だけセル画を重ね撮影する。同様にデジタル化画像で行ない圧縮する。映画なら、フィルム(アナログ情報)をデジタル化する。背景に当たるピクセルは同じ2進法数値、変化部分は異なる数値なので、コンピュータ内部で2画面の数値を比較し変化部分だけ取り出す(画像差分情報をとる)。背景部分と差分とを記録・伝送するのが動画圧縮の基本的考え方で、必要に応じ静止画像圧縮技術も併用する。圧縮はプログラムにより自動処理されるが、それが可能なのはデジタル情報だからである TV電話中の動き不自然 → コンピュータ処理速度より電話回線伝送速度遅い Ex. → 受信画像保存しコンピュータ再生 → 滑らかな動き ↔ 5秒の滑らかな動作データ送信に1分必要 電話は会話リズム優先し、画像は1/12送り音声とのタイミングを取る。CD-ROM画像も、改善されつつあるがCD-ROM装置読取速度が不十分だと装置とコンピュータ本体との伝送速度が遅くテレビほど滑らかではない 情報圧縮画像・音・文字処理の1研究分野ダウンロードファイル → 伝送時間節約に圧縮され実行可能プログラムファイルに戻す解凍作業必要 不可逆圧縮: 圧縮前の状態に戻せない圧縮 Ex. 画像圧縮は減色圧縮画像でも見えれば完全復元不要 可逆圧縮: 戻せる圧縮 Ex. 実行プログラム・文章、金銭出納簿等の圧縮は、完全復元しなければ無意味 動画圧縮表現形式: MPEG (.mgeg .mpe .mpg): 動画の、前と次のコマの相違部分を高速符号化し、データ圧縮、記録 Video for Windows (.avi) QuickTime (.mov) FLASH (.swf): Macromedia社Web用コンテンツ作成ツール「FLASH」のムービーファイル メディア融合DSP, Digital Signal Processer: 音声や映像などに各種のエフェクトなどの加工をするためのハードウェアNSP, Native Signal Processer: Intel発表のDSP機能をソフトウェア機能で代行する構想
75MHz Pentium + PCIチップにTriton + PCIバス実行転送速度100MByte/Sec以上必要 MP4映像・音声・字幕・静止画格納2001 MPEG-4 Part1:Systems (ISO/IEC 14496-1:2001)標準化(初) 2003 MP4 version2 (ISO/IEC 14496-14:2003)標準化 2004 MP4 AVCE (MPEG-4 Part15, ISO/IEC 14496-15:2004) 格納可能メディア
ビデオ: MPEG-1, MPEG-2, MPEG-4 Visual (MPEG-4 Part 2), H.264/MPEG-4 AVC(MPEG-4 Part 10), H.265(H.265/HEVC), AV1等 ImageJ (ImageJ)ビットマップ(ラスター) = 色(rgb)・形態・分布Ex. 年輪測定 力技: imagejで2点間結び、⌘Mで距離を出す(定規の方が早いかも) Phellodendron amurense: 環孔材は分かりやすい 方法: 年輪部分に印をつけ一括で測る - 画像処理をして自動認識できる構造なら簡単だが、印をつける作業は必要 1. 出来るだけ枝が水平となるよう回転(image → transform → rotate) 枝が曲がっていたら、水平にできるところで区切って回転 2. multi-point (icon)で矢印の真下の部分でY軸が一定になるようプロット3. Rawデータなら: analyze → measure (結果はエクセルとかで保存) スケールは入れておくと便利 |