Top
ヘッダー

(Upload on January 10 2019) [ 日本語 | English ]

Growth (成長)






Mount Usu / Sarobetsu post-mined peatland
From left: Crater basin in 1986 and 2006. Cottongrass / Daylily

Plant growth

size increase by cell division and enlargement, including synthesis of new cellular material and organization of subcellular organelles

growth and development

Measuring growth
fresh weight
dry weight
volume
length
height
surface area

[ photosynthesis | productivity | allometry | related to chemistry ]

索引

Absolute growth rate, AGR (絶対成長速度)

AGR = dY/dt ≈ (Y2 - Y1)/(t2 - t1)

dY: size
dt: time (e.g., year)
Y1 and Y2: size at t1 and t2, respectively
t1 and t2 time at 1 (beginning)and 2 (end), respectively

Growth curve (成長曲線)

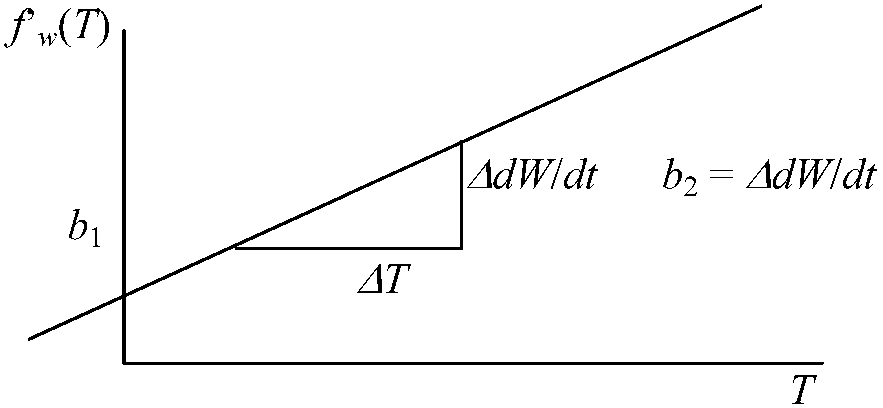
Growth analysis

Polynomial regression (Orloci & Kenkel 1987)
fw(T) = lnW = a + b1T + b2T2 … (1)
where W = the leaf area (LA) or sededling weight for a seed size class

T = the time at which the measurement is taken
a (constant) = the natural lograrithm of the initial leaf area or seedling weight
b1 and b2 (parameters) = related to the relative growth rate

Relative growth rate (RGR, f'w) of the leaf area and seedling weight →
f'w(T) = dW/dt = b1 + b2T × 2 … (2)
here, b1: intercept of relative growth rate

b2: slope of the relative growth rate
→ b2 > 0: increase of RGR, b2 < 0: decrease of RGR

Tmax: relative growth rate = 0 (hypothesis)

∴ Tmax = -b1/(2b2)

growth analysis
1) Logistic growth
= geometric growth or logarithmic growth

(Mitscherlich 1909)

a) Mitscherlich equation (ミチェーリッヒ式)
dY/dt = k(M - x) ⇒ Y = M - (M - x0)e-kt

k: proportionality constant (considered as efficiency coefficient)
t → ∞ → Y = M (M: maximum possible growth)

b) simple logistic equation

Issues on allometry

Sum is not the sum
Ex. considering two parts of biomass, e.g., stem (w1) and leaf (w2)

If w1 = aDb and w2 = cDd, then w1+2 = w1 + w2 = aDb + cDd
This equation is satisfied only when b = d [not realistic]

Productive ecology (生産生態学)

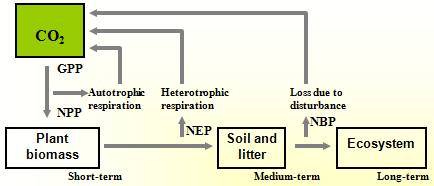
Productivity (生産力)

Gross primary productivity, GPP (総一次生産力)

= energy (E) or carbon (C) fixed via photosynthesis per unit time

Net primary productivity, NPP (純一時生産力)

= GPP - E or C lost via respiration (by plants) per unit time
= ΔB + L + G

ΔB = biomass change in the community between time 1 (t1) and time 2 (t2) = B2 - B1
L = biomass losses by death of plants or plant parts
G = biomass losses to consumer organisms

Net ecosystem productivity, NEP (純生態系生産力)

= NPP - heterotrophic respiration

Net biome productivity, NBP (純バイオーム生産力)

= NEP - loss due to disturbances
☛ productivity of biome type

NPP

Allometry (相対成長, アロメトリー)

Shape: an object encompasses all of its geometric properties except its size, position and orientation

Morphological integration: The covariation of morphological structures in an organism or of parts in a structure, which may reflect developmental or functional interactions among traits

allometry = allo (different) + metric (measure)
isometry = iso (same) + metric (measure)
relationships between two (growth) parameters → study to define the relationship between size and shape

(s.s.) The dependence of shape on size, often characterized by a regression of shape on size

y = αxβ ⇒ logy = logα + βlogx → Y = βX + a (linear equation)

β: coefficient of relative growth (相対成長係数)
If this equation is found between the two parameters, we call that allometric relationship

= dY/dX = dlogy/dlogx = (dy/y)/(dx/x) = (x/y)·(dy/dx)

t = 0 → α = y0/x0β
 Differentiated by t
1/y·(dy/dt) = β·1/x·(dx/dt) (Huxley 1932)

Ex. Relative daiameter growth rate, RDGR (Harper 1977)
RDGR = (lnD2 - lnD1)/(t2 - t1)

D1, D2: diameters at time 1 and 2, respectively

(Huxley 1932)

Isometry (等成長, アイソメトリー)
Geometrically similar objects exhibit what is called isometric scaling; the relationships between surface area, volume, and length
≡ β = 1 or integer

Ex. the relationships between surface area, volume and length

t-test, t = (b – β)/sb, sb = s2·y·x·Σ(X – m)2

(Rensch 1950)

Rensch's rule (レンシュの法則)

Rule in the relationship between the extent of sexual size dimorphism and which sex is larger
Across species within a lineage, size dimorphism increases with increasing body size when the male is the larger sex, and decreases with increasing average body size when the female is the larger sex
フッター