(2022年12月26日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 自然科学概論
科学 science自然科学 natural science: 自然現象natural phenomenaを扱う
scientia (L.) = 知識 → 整理体系化された知識 科学概論 philosophy of science, or grammar of science≈ 自然科学概論philosophia (G.) = philos 友愛 + phia 智: 当時は学問全体 (現在 哲学) → 自然科学体系化。目的・研究法明確化。知識・法則の成立範囲の特定等 → 人生観・価値観までを含めた哲学的思考の根拠 科学の発展形態(Chamberlin 1965)
市民科学 citizen science
|
一般人の科学理解(情報)欠如モデル (information) deficit model
一般人(非専門家) = 情報と科学的知識の受け手 ⇒ |
太古(原始社会) primitive society科学 = 生きるための野外生物学生物は生活する環境に適応した形や働きをもつ ↔ 生物は良く似た別の生物を持ち連絡する 黒曜石(十勝石)、原宿(群馬県)、白滝(北海道): 原石山(岩体として産出) → 矢尻等利用 黒曜石鉱床の品質と埋蔵量について必要な知識持つ [世界中 Ex. 欧州 - フリント] 化石: 貝・デスモスチルス - 装飾品、海棲: 海 → 陸化、火山 → マグマ |
BC 6000メソポタミア(バビロニア)エジプト天文学: ナイル川氾濫予測(暦必要) → 1年 = 365.25日幾何学: ピラミッド建設・ナイル川流域測量 Ames (≈ BC2000), エジプト: アーメスのパピルス(= リンド・パピルスRhind papyrus) 単位分数: 分子が1の分数 → 2/5 = 1/3 + 1/15, …, 2/101 = 1/101 + 1/202 + 1/303 + 1/606 円面積, S = (d - 1/9)² |
|
≈ ギリシア哲学 ギリシア自然科学 (= 古代オリエント科学)ギリシア時代 Ancient Greek era: 哲学的科学観 - 素朴な形での進化観演繹的公理 Ex. 大地不動で宇宙の中心 Xenophanes, Xanthus, Herodotus 陸上での貝の化石 → 昔は、その地が海であったと判断 a) イオニア(ミレトス)学派 Ionian Schoolミレトスに起るギリシア哲学初期の重要学派 = 唯物論的思想哲学者であると同時に商人や技術者であること多 三大問題
|A |C |B AB = 1, AC = x → CB = 1 - xφ = 1/x = x/(1 - x) → x2 + x - 1 = 0 → x = (-1 + √5)/2 ≈ 0.61803, φ = 1/x = (1 + √5)/2 ≈ 1.61803 [無理数] [長さ:幅 = φ]は最も心地よい釣り合いを持つ(経験則) 黄金長方形: 1/φ = φ - 1
→ オウムガイの殻など自然界に多 b) アテナイ431BC-404BC: ペロポネソス戦争 (the Peloponnesian war) → 政治力失うEudoxos (BC409-355): 比例。区分求積法 同心天球説: 惑星運行の数学的説明。太陽、月、5惑星の個々に恒星用の天球内を回転する別の天球を用意し、惑星が黄道上を動きつつ「8の字型(= ヒッポペテ曲線)」運動をさせる、完全モデルを目指す Menaichmos (BC350?-): 円錐曲線 Aristoteles (Aristotle, Aristote, アリストテレス) BC384-322 哲学: 論理学を大系づける「形而上学」 生物学の開祖 プラトンのイデア = 個物に内在する本質 → 本質はそれらが表す対象の外側に存在しない 個物 = 形相(限定するもの) + 質料(限定されるもの) プラトン・アリストテレス著作 → ギリシア哲学支配した観念論と唯物論は最高潮 → 後の哲学に影響 人心不安定さ反映し、ギリシア哲学は世界の本性より個々人問題へ関心移す 広領域の知識・経験体系化(自然学・天文学・物理学・動物学等) – それまでの科学からの進展 学問分類: 自然学(理論的) = 第一哲学, 数学, 自然学 + 実践的 + 制作的 第一哲学: 神-不変不動の純粋形相 目的論的: 事物にとっての善(遺伝子レベルでの個体)経験・物質: 重い物質は軽い物質より速く落下する(Galilei否定)。物体は力を加えると速度を生じる 宇宙モデル: 神聖な球。地球はそれを取り囲む全世界に比べて遥かに小さい c) アレクサンドリア期マケドニア: アレキサンダー大王(王子時代にアリストテレスに教受)建設都市c1) 前期Aristarchos (BC 310?-230?) |
Euclid, or Eukleides (BC300-?) プトレマイオス王招聘でアレキサンドリアへ来た学者? 「幾何学に王道なし」 Gr.; mathematics = Euclid幾何学 Euclid geometry (幾何学読本) → ユークリッド幾何学体系化 「エレメンツelements」全13巻 → 既存の数学に対し深い再反省 → 1理論体系とし再組織(5つの公理) Archimedes (BC287-212): アルキメデスの原理(浮力の原理) 天文学・数学・物理学(力学の開祖) Ex. 円周率。アルキメデスの螺旋 「円を踏むな」 → 兵士に槍で刺された Apollonios Pergaeus (BC260-200?): 「円錐曲線論」全8巻 Aristarchos (BC280?) 皆既蝕間に地球が月に落とす影を観測 → 地球と月の間の距離が地球の直径の約40倍と測定 恒星の観察できる視差の欠如 → 宇宙は無限 → 当時の人には受け入れられない概念 Eratosteres (BC275-194, BC237-197 or 236-194) 地球の円周距離算出 – 定量的学術 BC240?: 夏至正午の太陽高度 → 地球の大きさ推定(24900 miles) → 世界地図作成? 当時の常識より遥かに大きな値 – 一般には認められなかった C2) 後期BC146: ローマがギリシアを支配Hipparchos BC150?: 三角法(測量) → 三角関数。立体射影。球面天文学 Heron BC100?: 機械学、測量学 → ヘロンの公式 Menelaus BC100?: 「球面学」3巻。球面天文学の基礎を作る 2c頃 アレキサンドリア
卑金属 → 貴金属 → 錬金術 alchemy – 化学・医学と結びつく Lucretius Carus, Titus (ローマ) BC94-AD55? Ptolemaios Claudios, or Ptolemy 85-165: アレクサンドリアで活躍 天文学・占星術・地理学・光学 「アルマゲスト」(原題「数学的集成」) 13巻: バビロニア、エジプト、ギリシャ天文学集大成 「地理学入門」1巻 「プラニスファイリウム」 立体投影法 – 円錐図法 球面幾何学、太陽・月・惑星の運動理論 BC8 c月食記録等(観測記録資料価値大) 天動説 Ptolemaic theory = 天体観測↔ 地球中心説 geocentricism = 地球球体(大地不動で宇宙の中心) Diophantos 300?: 整数論 Arithmetica= 近世整数論の基礎 → 負数はまだない インド数学アラビアを経てヨーロッパへ = ヨーロッパ中世数学形成に影響0(ゼロ)の発見 → 10進法 Q. 10進法では3桁の数は100x + 10y + zの形に書ける。x + y + zが3で割り切れれば、この数を3で割り切れることを示せ 2次方程式 → 負数概念必要(インド)Aryabhata 476-?: 現在の2次方程式と同じ解法で解く 「アールヤバティーヤ」 数学教科書 Brahmaagupta 598-? 「ブラーフマスプタ・シッダーンタ」 数学教科書 (Aryabhata批判) ブラマグプタの定理: 円に内接する四角形ABCDの対角線ACとBCが点Pで直行すれば、PからABへ下ろした垂線PHを逆に延長したものは、辺CDの中点Mを通る 6-7 c: インド記数法体系 = 10進法完成 Bhaskara 1114-?: 2次方程式には2つの解があることを示す 「リーラーバティ」「ビージャガニタ」 - 数学書 「シッダーンタシロマーニ」 - 天文学書 Bibhutibhusan Datta 1888-: 「インド数学史」 |
アラビア科学(イスラム圏科学)古代オリエント科学から発展7c中(ウマイア王朝)-8c中(アッバス王朝): 発展始まる アリストテレスのギリシア語諸著作をアラビア語へ翻訳し注釈行う 8-9c: アラビア・ルネサンス9c: 天文学: ダマスカス、バグダッドに天体観測所
プトレマイオス、ガレノス、エウクレイデスらを含むギリシア語著作をアラビア語に翻訳 ヨーロッパ暗黒時代 the Dark Ages西欧 < 10c終: キリスト教神学とその支柱である哲学が影響 1085 キリスト教徒トレド奪回
→ アラビア語翻訳ギリシア哲学がキリスト教圏に入る "Liber Abaci 算盤の書": インド・アラビア数学・記数法・計算法紹介 Bacon, Roger 1214-1294: 実験科学 – 近代科学の萌芽「自然認識にはまず数学と経験を主とすべき」 → 教会拒否し異端者扱い |
数学発展 (数学史 mathematics) Abel Niels Henrik 1802-1829
発散級数は和を持たない
1736: 1/12 + 1/22 + 1/32 + … = 6/π →Def F: 面数, E: 稜本数, V: 頂点数 → Formula: V – E + F = 2 表. ヨーロッパ中世後期の諸技術を中国と対照 → 宗教観の差. * 751: サマルカンド、793: バグダッド、900: エジプト、1100: モロッコ、1150頃: スペイン、1189までに: フランス羅針盤 黒色火薬 火砲 鋳鉄 紙* compass 中国 11c-12c初期 9c前期 竹筒ロケット 古くから BC4 1c末 欧州 12c後期 13c 13c末(1325に記録) 13c 12c 印刷術 機械時計 版木 土製活字 木製活字 金属活字 中国 6c 1045頃 1314頃 1392(朝鮮) 11c 水時計 欧州 1289 → → 1450 Gutenbrerg J 1450 脱進器 (1400-1466?) 15c末 ゼンマイ時計 |
[ 地球誕生仮説 ]
産業革命 industrial revolution → 哲学革命
近代科学成立期= 科学革命「天体の幾何学から天体の力学へ(天文学)」Regiomontanus 1436-1476, 独, 天文学 + 三角法 当時の惑星表(航海に必要)の誤り指摘 – 地動説の伏線 Vinci (da), Leonard 1452-1519, 伊 多分野(美術・建築・技術科学)で活躍 「人体解剖図」 Copernicus, Nicolaus 1473-1543, Poland 1500頃 アリスタルコス(BC310?-BC230)地動説知る → 太陽中心説より天体運動説明容易
太陽中心、地球と共に数個の惑星。地球・月は自転(地動説) → ケプラー 容器に水蒸気を詰め、それを冷やし凝集させて真空を作る装置(1606) Digges, Thomas 1546-1595, 英: 天文学 コペルニクス体系を取り入れ無限の宇宙を擁護 Stevin, Simon 1548-1620, 蘭: 数学・土木技師 小数発見。風力帆走2本マスト自動車Simon of Bruges発明 Kepler 1571-1630, 独: ケプラーの法則 Tycho Brahe 1546-1601, デ: ケプラーの師。膨大な天文観測データ Galileo Galiei 1564-1642, Galilei姓 (当時伊習慣で名, 数・天文・物理・哲学)近代物理学開幕 = 観察による科学研究法の基盤
振子振動観察(逸話) → 周期一定 = 振子法則 → 振子時計設計(不完全) Torricelli E 1608-1647 伊, Galileiの弟子 水銀を詰めたガラス管を倒立 → 真空の存在(原子論) van Helmont, Jan Baptista 1577-1644, ベルギー: 実験科学(錬金術)→ 物質 = 質料 + 精気
→ 精気単離を試みる → 空気とガスを区別 リンカーン州ウールスソープ生まれ。ケンブリッジ大学卒業の後に教授 万有引力の法則 → 機械論的・力学的(物理的) 1687 「自然哲学の数学的原理」(略, プリンキピア) (自然哲学 natural philosophy = 物理学): 力学的自然観
a) 実験と帰納 + 演繹 Laplace PS 1749-1827, 仏: 星雲説改めて提唱(カント-ラプラスの星雲説) ラプラスの魔 「ある超能力者が特定の瞬間におけるあらゆる状態(全ての粒子の速度と位置)を知れば、そのものは将来のあらゆる出来事を予見できる」 → 瞬間の状態は時間の関数で表現できる 自然史的地球観誕生984 Erik the Red (赤毛のエリック)グリーンランド発見1492-1498 Columbus,Christopher (1451-1506) アメリカ大陸(西インド諸島)発見 Agricola G 1490-1555, 独: 鉱物学の先駆的研究 Leonardo da Vinch: 「地質と化石」1504-05 化石とは地層の中に存在(古)生物遺骸 → 流水による侵食と堆積 Steno 1638-87: 地層学(層位学、層序学) 累重の法則(1669): 地層 – 水平, 空間 – 時間 地球生成説: 水が全ての元 – 水成論 堆積岩生成では正しいが、多事例で間違い (Ex. 花崗岩・変成岩が海中でできるとした過ち) |
de Buffon, GL Leclere 1707-1788 地球は最初は溶融状態で現在の温度になるまで7万8400年かかった(1749) 根拠: 鉄冷却必要時間を鉄体積を変え計る ↔ 聖書: 天地創造後6000年 数回大洪水(1749) → ソルボンヌ大呼出: 聖書 ノアの洪水は1回 → 説変えるKant I: 天界の一般自然史および理論(1755) 地球誕生 → 発展 → 現在 → 消滅 Hutton J 1726-1797, 英: 「地球の理論」(1795)現在の地表の諸現象を調べれば過去の変化が推定できる Werner A 1749-1817, 独: 岩石成因 – 水成論 → 火山作用は二次的なもの ↔ Humboldt Av 1769-1859, 独: 火成論 Herschel FW 1738-1822, 独(活動は英): 反射望遠鏡製作 → 天王星発見 Smith, William W 1765-1839, 測量技師 運河掘削・石英採掘 → 化石による地層同定(対比) (1916-19)
標準化石の方法 Ex. 白亜・ジュラ紀 – アンモナイト 周期表 (周期律表, periodic table)元素 element: 同数の陽子を持つ原子のグループ表. 長周期型元素周期表 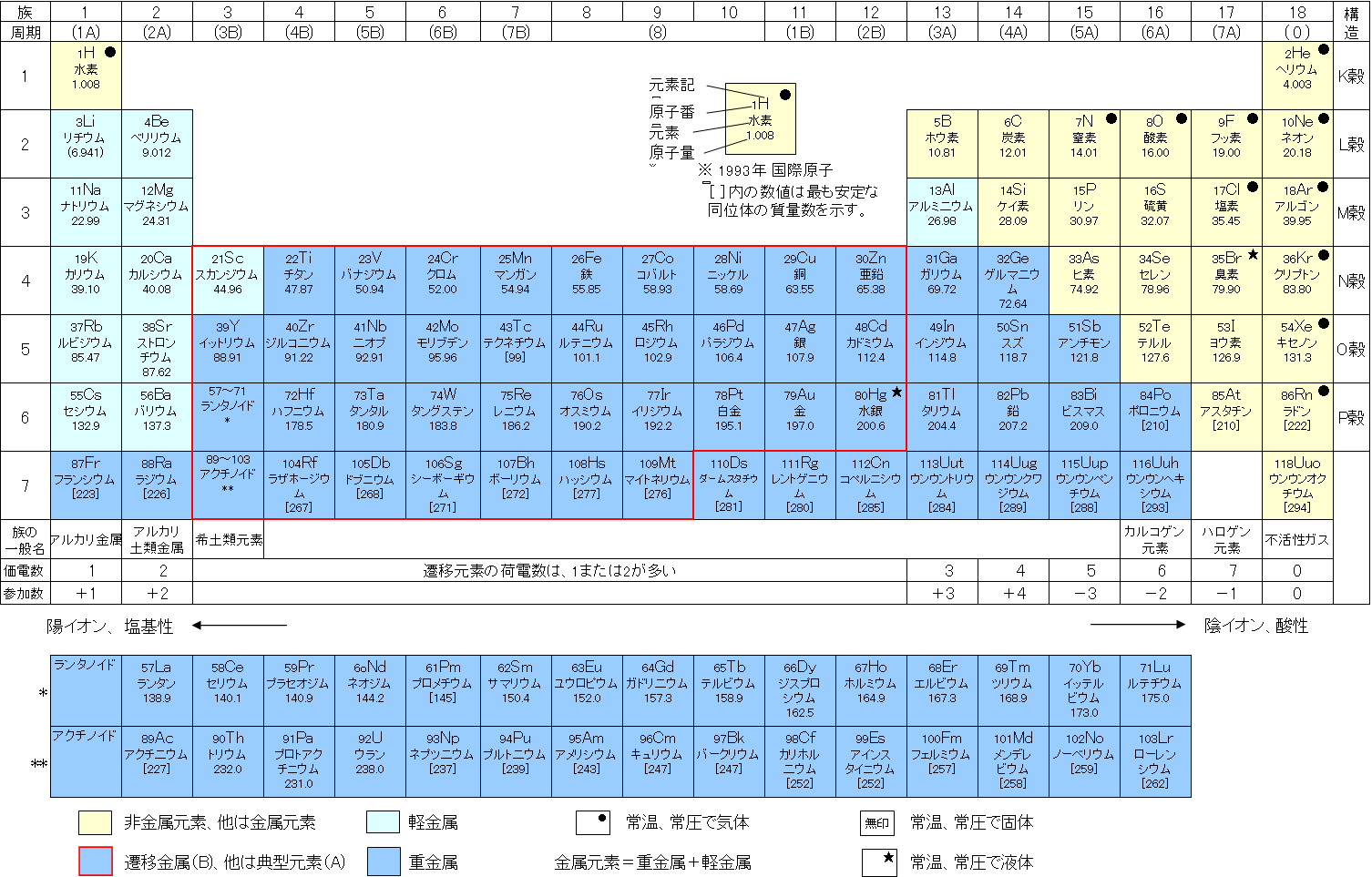
国立天文台(編). 2010. 理科年表 2010版 周期律: 元素の原子が規則性ある構造持つ → 元素は構造要素に分割可能人工元素 synthetic elements: 原子番号93-109のもの ↔ 天然元素 同素体 allotrope: 同元素だが互いに性質・構造異なる単体
同素体を持つ元素: S, C, O, P (scop) 炎色反応 flame reaction: 金属定性検出
白金線につけバーナーの無色炎で強熱 → 各金属特有の色 Ex. Al: 2Al + 6HCl → 2AlCl3 + 3H2↑
2Al + 2NaOH → 2NaAlO2 + 3H2↑ |
[ E ≡ energy ]
|
1919 Rutherford: N原子核にα粒子衝突実験 714N + 24He → 11H + 817O = 原子核は人工的変換可能証明 Def. 11H = 陽子 proton ⇒ 衝突実験から11H得られ最も軽い原子核と推定Def. 質量数: 原子核質量を水素原子核(11H)の整数倍で表す Ex. H = 1 1932 Chadwick (英): 49Beにα粒子衝突実験 24He + 49Be → 01n + 612CDef. 01n = 中性子 neutron ⇒ 01n: 陽子とほぼ同じ質量をもつ中性の粒子 Def. 核力(核結合力) nuclear (binding) force: 核構成する陽子や中性子の結合力 (電気力ではない) Def. 原子核 (atomic) nucleus(+e) [= 核子 nucleon]
= 陽子(+e) [1.6726·10-27 kg] + 中性子(0) [1.6749·10-27 kg] Def. 電子 electron (–e): 陽子・中性子の質量の約1/1800 [9.109·10-31 kg]
電子雲: 電子の確率分布 → 直径0.5-2Å = 原子の大きさ Ex. 天然水素同位体
1H. 2H = D (重水素 deuterium). 3H = T (3重水素 tritium) = 放射性同位核、放射性同位元素 安定同位体 (stable isotope): 放射能持たない Ex. 12C, 13C (応用)原子モデル1) トムソンモデル (1903): 原子中に電気性物質散在(一様分布)
= ブドウパンモデル: 正電荷のゼリー中に電子が散らばる = 土星型原子模型: 原子の中心に+電気集まり、周りを-電気が軌道運動 Bequerel, Antoine H. 1852-1908, Frederic Joliot-Curie 1900-1958, 1903 長岡半太郎 1910 Rutherford, Ernest 1871-1937, 英/Bohr NHD 1885-1962, デンマーク
実験で長岡モデル支持
α粒子: その質量の1/7000負電荷(= 電子)に衝突しても反撥しない
原子核大きさ ≈ 10–15 m α粒子の最初の運動Eから大きさを計算した 原子論 vs ニュートン力学/熱現象粒子運動= 質点運動の法則: 粒子の従う運動法則 (ニュートン力学の範囲)= ニュートンの三大法則 1st law. 慣性の法則 2nd law. ニュートン方程式 Ex. ≈ 光速 → mは変化し運動量は時間的に変化
p = mv ⇒ 特定座標系(Ex. 慣性系)でのみ成立 → Ex. 軸毎に時間の進み方異なり、時間と共に質量変化 地球に固定した座標系と火星に固定した座標系では軸が異なり、両方を包括するためには座標系を太 陽に固定、更には銀河へと行く → 固定した座標系はあるのか 3rd law. どの座標系で加速度を計るかα = m·d2x/dt2 = fx ⇐ m·dv/dt = f (dt: 定時間の存在) if 第3法則が成立しないと2物の力の差は異なり物体は常に加速度を有する
⇒ 第1法則も否定 ← 矛盾(背理法により第3法則成立証明) → その運動体が規則正しいというのはどのようにして知る事が出来るのか。という、堂々巡りが始まる ある時計の振動と天体の運動(地球の公転の時間を基準に時間は決められた)とは、法則的に一致
→ この段階での"時間"とは絶対時間認識の元で形成 ⇒ 時間とは、物体運動の認識として表わされる 運動方程式の帰結1. 初期条件 (f: 位置座標、ベクトル): dP/dt = f, m·dv/dt = f, f = fx + fy + fz運動法則 ⇒ 運動量変化(加速度)の仕方を決める ⇒ 初期形態が運動法則を決定しうる物ではない 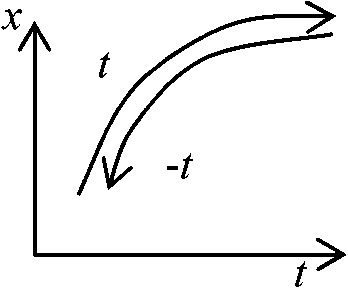
時間反転 (t → -t) 運動方程式普遍
md2x/dt2 = f … (1) → dm/dt·(dx/dt) = f (Boltzmann, Ludwig 1844-1906 自殺) H-定理熱力学第2法則を運動力学から説明n(r, v, t), H(t) = ∫dvdrnlogn, dH/dt < 0, S = -rH ⇒ 力学現象の可逆性と熱現象の不可逆性を示す 熱力学の原子論的基礎
縦↑↓, 横↔との分子の割合: 垂直か水平に運動 –
= UdA(n→ + n←)VnA____(n→ + n←) = N ⇔ トータル
∵ n↑ + n↓ = N↕ |
縦横分子数の時間的変化
縦方向分子数の時間的変化 dN↕/dt ⇒ Increase = pN↔, Decrease = pN↕ → p(N↔ – N↕) 横方向分子数の時間的変化 dN↔/dt ⇒ Increase = pN↕, Decrease = pN↔ → p(N↕ – N↔)
↓ 分子の分布状態が等しいものと仮定 → 衝突 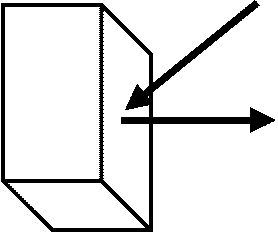 過去から現在を見る: 縦方向の増加は横方向から来た分と縦方向から消えた分の差
過去から現在を見る: 縦方向の増加は横方向から来た分と縦方向から消えた分の差
pN↕ – pN↔ = p(N↕ – N↔): 衝突 → 分子は等しく分布 dN↕/dt, dN↔/dt, Ce2pt → 変化量 古典論の限界天体: 星は見えないはず水素原子 hydrogen atomの安定性 → 不確定性原理 (運動状態の捉え方が違う) 夜空の星: 総ての星 → 質量の4乗に比例するE(= 太陽Eと仮定) Ex. 乙女座南方の恒星 αケンタウルス(αK): 太陽に最も近く距離4.3光年 → 太陽とおよそ同じ発光量の0等星 同星から2 × 10-8 (W/m2)のEが地球に届く 実際: 地球公転軌道を用い三角測量で星への距離求め、星から届く光量から星発光量が分かる
→ 等星を見るには1/10 × 300 = 30 (s)間見つめないと見えない 1個の持つ光粒子Eはレチナール分子の状態を変える程の大きさを有している 光が物質と作用し、そのEが物質に吸収される時は、光Eは波ではなく光子という粒子として吸収される(田中 1973) 可視光の光子E: hv(yellow) = 3 × 10-19 J, hv(violet) = 5.2 × 10-19 J等 ≫ 1 eV = 1.6 × 10-19 J
100個ほどの光子が届けば視神経細胞分子は光感知 = 星はすぐ見える 光の波動説・粒子説の比較光が波の時の条件: 全部のレチナール分子の状態が変わる光が粒子の時の条件: 30個のレチナール分子の状態変化すればよい
(3 × 1010)/d2 (cal/cm2·min) × 1/4 × 1/60 × 1/30 × 6 × 10-20 (cal) ボーア原子模型 Bohr atom modelBohr Niels HD 1855-1962, デンマーク: H等、簡単な原子で成立対応原理 coresspondence principle: 古典力学-量子物理学間法則統一を模索 → 量子模型 quantum model 1) 電子 = 核との間のクーロン力の作用で核の周りを等速円運動する ボーアの量子条件: 2π(mva) = nh
n = 1, 2, 3, …: 量子数 ボーアの振動条件: v = (Em – En)/h
Em: 遷移前のE
E状態(E準位energy level) = 基底状態と同じ角運動量を持つ 確率的に決定 ⇒ 不確定性原理 uncertainty principle (Heisenberg uncertainty principle) Ex. オーロラ aurora
電子がE受け取る → 原子核から遠い軌道を回転 → 励起状態 [不安定] → 元の軌道に戻る = E放出 ⇒ Eが光として放出される → オーロラ Ex. O = 557.7 nm + 630.0 nm 応用: 流星: 発光色により成分推定 原子物理学概論試験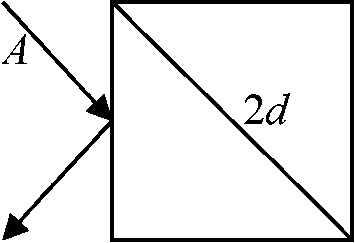 1. 2種類の分子(A, a)から成る分子系が相互作用をしている。Aは密度ρAで分布し境界面は水平方向に45°であり質量は大きく固定した位置にある。回転もない。aは密度ρaで分布しており水平方向と垂直方向にのみ運動している。時刻tにおける垂直方向の分子の総数をN1(t)、水平方向の総数をN-(t)、この差をD(t) = N1(t) – N - (t)とする。次の2つの考え方にもとづきD(t)を求めよ。分子aの速さをv、分子Aの垂直断面の対角線の長さを2dとする
1. 2種類の分子(A, a)から成る分子系が相互作用をしている。Aは密度ρAで分布し境界面は水平方向に45°であり質量は大きく固定した位置にある。回転もない。aは密度ρaで分布しており水平方向と垂直方向にのみ運動している。時刻tにおける垂直方向の分子の総数をN1(t)、水平方向の総数をN-(t)、この差をD(t) = N1(t) – N - (t)とする。次の2つの考え方にもとづきD(t)を求めよ。分子aの速さをv、分子Aの垂直断面の対角線の長さを2dとする
i) 垂直、水平方向の分子のうち4dvρaが1個の分子Aにより単位時間に水平垂直方向に運動方向を変える |
|
⇒ 微視的世界の法則: 量子説(論) quantum theory (Planck 1900) Def. 量子 quantum: 物理量が分割されない最小単位から成り立つもの 熱放射 heat radiation (熱輻射 thermal radiation): 金属等を熱すると暗赤色・橙黄・白の光を放射 → 熱放射は可視光線visible lightを含む幅広い波長分布を持った電磁波 Def. (完全)黒体 black body: 物体表面を処理し、外部から入射した熱放射を全て吸収する物体(理想的)黒体放射(黒体輻射) black body radiation (空洞放射cavity radiation) → 物体種類・表面状態に関係ない 量子力学的状態では ⇒ ΔxΔp ≥ h/2(調和脈動子 = 成立)
仮定: 振動数fの光の持つEの大きさはhfの整数倍に限られる ⇒ 量子論の始まり ∵ 整数倍となる = 光は計数可能 ⇒ Law. プランクの放射法則 Planck's law of radiation (Planck 1900)
振動数 v (波長 λ), 絶対温度 T 黒体放射は温度のみの関数で表せる = 黒体放射の具体的記述 c = 真空中の光速(≈ 3.00 × 108 m/s) 振動数 v, v + Δv, [v, v + Δv]間にあるE UvΔv (/cm3)
Uv = (8π(kT)3/h2c3)·P(x), x = hv/kT Uλ = D·(1/(e(hc/kTλ) – 1))·(1/λ5), D = 8πhc (constant) 黒体放射EはTのみで決まる波長λp(T)で極大値を持つ Law. (rewrite). プランクの法則I(λ, T)Δλ = (2πhc2/λ5)·(1/ehc/lkBT – 1)·Δλ (J/s·m2) Def. ボルツマン定数 Boltzmann constant, kB (or k) = 1.38064852 × 10−23 J·K−1 Def. プランク定数 Planck constant, h = 6.62607 × 10-34 J·s= 6.6262 × 1027 erg·s = 1.58 × 10-34 cal·s Def. ディラック定数 Dirac constant (換算プランク定数 reduced Planck constant), ℏ= 1.0545887 × 10-34 (J·s) = 1.0545887 × 10-27 (erg·s) プランクの法則より導かれる2つの法則Law 1. ウィーン(の変位)則 Wien's (displacement) law (Wien Whilhelm 1864-1928): 波長当りの光量子量(E量)が最大となる波長, λmax ⇒ λmax ∝ 1/T (高温物体ほど短波長の電磁波放出)
黒体放射 ⇒ λT = constant (2897), λ: 波長(μm), T: 温度 ⇒ 短波長で実測と一致 ρλ = (2πckBT)/λ4 (c: 光速, kB: ボルツマン定数) ⇒ 長波長で実測と一致 (Rayleigh, Jeans) Law 2. シュテファンの法則 Stephan's law
⇒ W = 5.67 × 10-8T4 (W)
I*, 単位面積から単位時間に放射される全E量 Law. キルヒホッフの法則: 放射率 = 吸収率 ⇒ 放射をよく吸収する物体はよく電磁波を放射  ⇓ 両式矛盾解決 (Planck)
⇓ 両式矛盾解決 (Planck)
量子説重ねあわせ可能: ψ1(x) + ψ2(x)
Δx: 位置の幅
x軸方向の運動量の幅: Δpx = Δ(px – pxavg)2 → (Δpx)2 = (px – pxavg)2 中性子 (neutron)中性子束(中性子束密度) neutron flux: 中性子挙動が集団としてもつ効果を記述するため導入された量中性子流密度ベクトル(中性子流) neutron current density vector: 中性子の流れ 定量的に表現する場合は、流れの方向に垂直な単位面積を通り単位時間に流れる正味の中性子数 熱中性子thermal neutron: 原子核の熱運動のEと同程度のEをもつ中性子20°Cの媒質中では熱中性子のEは約0.025 eV。2200m/sの付近にマックスウェル分布 高速中性子 fast neutron: 一般にEが0.1 MeV 以上の中性子cf. 冷中性子(冷たい中性子) cold neutron 中性子寿命 neutron life time: 中性子は吸収・漏洩等で体系中に存在しなくなる。このとき中性子の平均的寿命1900 Planck Max EL 1858-1947, 独
プランク量子仮説 = Eはある単位量の整数倍で表現可能 作用量子action quantum ≡ hv 熱放射に関する式 ρλ = (8πhc/λ5)/(1/ehc/hTλ–1) → 実測値とよく一致 1905 Einstein: 光量子仮説 light quantum hypothesis= E粒子存在 1887 Hallwachs, Wilhelm 1859-1922, 独
ハルワックス効果(光電効果 photoelectric effect) ↔ 逆光電子放出 inverse photoemission = 逆光電効果 inverse photoelectric effect UV照射で真空中に負帯電した物体(金属)が電荷を失う現象 → 電子放出による Def. 光電子 photoelectrons: 飛び出てくる電子 光起電力効果 photovoltaic effect: 物質に光を照射することで起電力が発生する現象。光電効果の一種
→ 光起電力 photovoltaics → 光起電力変換 photo voltaic conversion 光電管(光電効果利用し光Eを電気Eに変換) + 電流増幅(= 電子増倍)機能
光電子放出の第1法則 first law of photoelectric emission 熱電子 thermal electron (thermoelectron): 金属等の表面を加熱 → 表面から熱励起され飛び出す電子 von Lenard, Philipp EA 1862-1947放電効果特性 – 1, 2, 4は古典力学で説明不可
⇒ 量子説採用: 光は光量子(光子) photonというEの塊からなる (cf. 音子 phonon)
電子が飛び出す条件: hv > W = hv – W |
量子的状態と物理量コンプトン効果 Compton effect (Compton Arthur H 1892-1962): トムソン散乱の他に、入射X線より波長の長いX線が散乱される
トムソン散乱 Thomson scattering: X線が物質に入射 → 入射X線と等しい波長のX線が散乱
X線を原子結晶に照射 → 回折X線が干渉縞生じる
入射X線: Eの1部を電子に与え、より小さいEのX線となり散乱する 物質波 matter wave= ド・ブロイ(の物質)波 de Broglie matter wavede Broglie Louis V 1892-, 仏 1923 物質波概念 → 電子も波動とみなせる 1927 実験的に証明される ⇒ 電子波 electron wave 1924 ド・ブロイ波長 de Broglie wave length, λ: 光 = 光量子 → 物質波存在
λ = h/p = h/mv (m: 質量, v: 速度) Def. 運動量, p = mv ⇒ λ = h/√(2meV) = √(105.4/V) × 10-10 (meter)
2πa = nλ (n = 1, 2, …), a: ボーア半径, λ: 電子波波長(ドブロイ波長) Ex. 音 ↔ 力学的でない波 Ex. 電磁波 波動力学 wave mechanicsSchrödinger Erwin 1887-1961, オーストリア
観測可能な量と概念のみから構成(実証主義的) 対応原理 → マトリックス力学 = 波動力学 → 「量子力学」に統一 水素: ニュートン運動方程式
E = -e2/(2r) [ポテンシャルエネルギーの半分] 毎秒電磁波を放出(減少) m(-v2/r) = -e2/r2 → α = v2/r = e2/mr2 rに関する微分方程式
dE/dt = d/dt(-e2/2r) = (e/2r2)·dr/dt … (2)
e2dr/(2r2)dt = (2e6)/(3c3m2r4) … (1) 量子力学の構成 量子力学的状態: ψ(r) ⇒ 位置座標の関数
量子力学的状態: ψ(r) ⇒ 位置座標の関数重ね合わせ可能: ψ(r) = ψ1(r) + ψ2(r) ⇒ 加えたもの
→ やはり量子力学的状態を(波動の様に)示す
物理量___作用素 物理量の値: ∧cr: 座標と運動量の関数 ↔ –iħ∀(φ(r)) = λφ(r): 固有値 状態の時間変化: iħ∂ψ(r, t)/ψdt = H(r, –iħ∨)ψ(r, t) ⇒ 座標と運動量(Schrödinger方程式) 物理量の期待値: ∧exp = ∫ψ*(r, t)∧(r, -iħ∨)ψ(r, t)dr 量子力学の作用素: 古典 → 量子
x, y, x → x, y, z ⇔ 運動量 = 1つの実数(古典) / 1つ1つの作用素(量子) エネルギーの作用素
古典__________________量子
運動量のx成分 Ex. 60 kgの人が10 m/sで走る:
p = 60 kg/10 m/sec = 6 × 104 × 103 cm·g/sec = 6 × 107 cm·g/sec
z成分: xpy – ypz > –iħ(x∂/∂y – y∂/∂x) 角運動量の2成分を同時に確定することはできない → 大きさと1成分が同時に確定した値を持つ
動径方向の運動, l = 0 1 2 3
ナトリウムスペクトルの特徴から名付けられる エネルギー作用素 H = (r/2m)p2 – e2/r → (-h2/2m)·v2 – e2/r 運動EとポテンシャルE [(h2/2m)(∂2/∂x2 + ∂2/∂y2 + ∂2/∂z2) – e2/r]Ø(r) = EØ(r) 固有方程式 (E: 水素原子のE) E = -(e2/2a)(1/n2) = -(2m/2h2)(1/n2)
a: ボーア半径 Bohr radius 電子の質量: 換算質量 μ = mM/(m + M) ⇒ m/(1 + m/M) ≈ m |
|
Def. 電子殻 electron shell: ボーア原子模型で原子核取巻く電子軌道の集合
原子に束縛された電子の状態を理解する上で重要 - 電子配置 (イオン化や化学結合を決める) Def. 内殻電子 core electron: 価電子軌道より内側にあるもの
原子間化学結合や、物性に影響しない ↔ 原子構成電子の振舞 → 原子核による静電ポテンシャル中の3次元シュレーディンガー方程式を解き得る 電子雲 electorn cloud: 分子やイオン形成時に重要 ⇒ 電子軌道: 主量子数n、方位量子数l、磁気量子数mの3つで指定n: 軌道の大きさとEを決定 (n = 1, 2, 3 …, i, …, n: integer)
= 電子殻K殻、L殻、M殻 … に対応: K殻にある電子E最小 l: 軌道の形を決定(l = 0, 1, 2, …, n – 1) = s軌道, p軌道, d軌道, f軌道 … に対応
: n 1 2 3 4 図. 電子配置 m: 各軌道を決定(-l, -l + 1, …, 0, …, l - 1, l, m: integer) Ex. n = 2, l = 1を総称し2p軌道 → 3種類のm = (-1, 0, 1) → 2px, 2py, 2pzの配位をもつ3軌道存在 電子 ≡ フェルミ粒子Ax. パウリの排他原理: 1軌道には互いに逆向スピン持つ2電子しか入れない Def. 電子対 electron pair: 軌道を2つの電子が占有した状態 ⇒ 電子対生成
Ex. 2p軌道 = 最大6電子収容_Ex. 3d, 4d等のd軌道 = 10個 R: リュードベリ定数 Rydberg constant (≈ 109700 cm-1)
電子捕獲 electron capture Ex. K捕獲 K-capture 原子中の電子のE状態
水素原子のE
水素原子原子の中のE状態Ex. 水素原子のE
1s (l = 0の時) → n = 1__ ・ 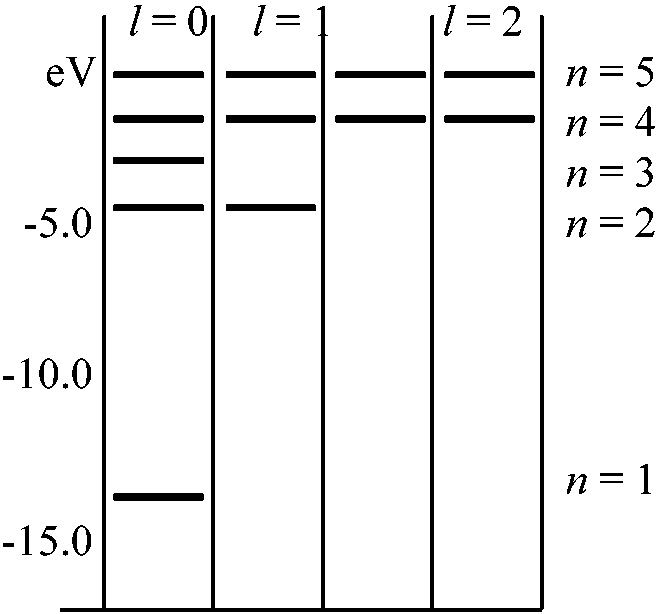 角運動量の固有状態(l = x, M = y)
角運動量の固有状態(l = x, M = y)水素原子のE準位
電子がどのようなEを受け取るか 1. 相対論的補正
ΔE = (Z2d2/4n2){3 – 4n/(l + 1/2)}|En|
電子の磁気能率: μ, 原子核による磁場: H, E: W |
多原子系と原子価: μ, H, Wの表式[μ] 荷電, q ⇒ 一周時間, T = 2πr/v 半径: r ⇒ s: 面積 速さ: v ⇒ c: 光の速さ
iT = q ⇒ 電流 i = q/T = qv/2πr 角運動量: σ 
μの向き↑, δの向き↓ H = ZeLe/mcr3, cr↑: 単位ベクトル [W] = -μH = –{(–e/mc)·(h/2)·σ}·(Ze/mc)(Le/r3) = Ze2/(mc)2·1/r2·(h/2)·σLe
相対論的補正
↑↑ΔE = (Z2α2/4n2)·4n/{(2l + 1)(l + 1)}|En|
1. 全補正 ↑↑(z2α2/4n2)·|En|·[3 – 4n/(l + 1/2) + 4n/{(2l + 1)(l + 1)}]
= z2α2/4n2·|En|·{3 – 4n/(l + 1)} ↓↓(z2α2/4n2)·|En|·[3 – 4n/(l + 1/2) – 4n/{(2l + 1)l}]
= z2α2/4n2·|En|·(3 – 4n/l) = z2α2/4n2·|En|·{3 – 4n/(j + 1/2)} 真空で電磁場ができたり消えたりしている 固体のEバンド(バンド)Ex. 水素ガスを圧縮し固体にする → 原子間距離↓ → 原子間相互作用↑
価電子帯(充満帯): 価電子入るバンド → 伝導帯 conduction band 原子核E+〇 ⇔ 〇- ZAXの質量m(ZAX)は質量数Aにほぼ比例 ≠ 精密測定では異原子核結合E binding energy of nucleus (1核子の結合E binding energy of nuclear particle) 質量 12C: Mass = 12 (原子質量単位atomic mass unit, a.m.u., AMU)
原子 = 12 AMU (1 AMU = 1.6605655 × 10-24 g)
mp = 1.6726485(86) × 10-24 g
E = [M(ZN) - ZmH - Nmn]c2 = -B (核)質量欠損 (nuclear) mass defect: 原子核を作っている核子の質量の和からその原子核の質量を引いた値 核磁気共鳴(磁気共鳴) nuclear magnetic resonance, NMR原子番号と質量数が共に偶数ではない原子核 → 0でない核スピン量子数Iと磁気双極子モーメントを持つ⇒ 原子 ≈ 小磁石 → 磁場をかけると磁石(原子核)は磁場ベクトルの周りを一定周波数で歳差運動 Def. ラーモア周波数 Larmor frequency: 原子核の磁気双極子モーメントの歳差運動の周波数Def. 核磁気共鳴: 原子核に対しラーモア周波数と同周波数の回転磁場をかける → 磁場-原子核間に共鳴発生
磁場中の原子核はゼーマン効果で磁場強度に比例した一定E差持つ2I + 1個のE状態 核磁気共鳴分光法 nuclear magnetic resonance spectroscopy, NMR: 核磁気共鳴でスペクトルを得る分光法 |
|
中性子 → 電子electron + ニュートリノ(中性微子) neutrino + 陽子 陽子 → 陽電子(ポジトロン) positron + ニュートリノ + 中性子 1934 湯川秀樹(1907-1981): 中間子理論(中間子論 1935)
→ 核力の原因は中間子存在し、それが核子間でやりとりされる d ≈ 2·10-15 m → パイ中間子質量は電子の質量の200倍と予測 1947: パイ中間子が発見実証される Def. 素粒子 elementary particle: 物質を構成する最小単位 = それより小さな存在がない(他分野に影響)
= 内部構造持たない = 空間的な大きさを持たない ⇒ 素粒子の空間的対称性 = 全原子は左右対称 1956: 李政道・揚振寧 (中国, ノーベル賞): パリティーの法則否定クォーク: 6種類 = アップ + ダウン + ストレンジ + チャーム + トップ + ボトム ハドロン: クォークから構成される粒子
中間子: クォーク-反クォーク対で構成(偶数個フェルミ粒子 → 中間子自体はボース粒子) + パイ中間子
バリオン数の保存則 law of conservation of baryons
Def. ハイパーチャージ = ストレンジネス + バリオン数 素粒子を見る加速器 accelerator: 多くの粒子 - 自然界に殆ど存在せず加速器で発見研究
コックロフト・ウォルトン装置 Cockroft-Walton's apparatus: 高電圧人工加速装置(1932完成)
リングの数箇所に粒子加速管挿入。電子陽子はリング中回転し、加速管を10万回/sec以上通過し、その度にE増大。電磁石の作る磁場強度は、粒子E増大に同期し増大され、粒子はそのEに関係なく常にリング内で同軌道描き加速され、電子陽子は光速位まで加速される シンクロトン放射(放射光) synchrotron radiation: 加速器(蓄積リング)から得られる電磁波 カミオカンデ KamiokaNDE, Kamioka Nucleon Decay Experiment (小柴昌俊, 2002ノーベル章)1987: 超新星爆発からのニュートリノ捕える 4つの量子数 quantum number
1原子中で2電子が4量子量全てに渡って同値はとれない H. エルゴード仮説 時間的平均(仕事) ≡ 空間平均(経路)バークホッフ Birkhoff: 位相空間 = 粒子の自由度の数だけ座標軸がある
N2 → 6N次元 = 3N(運動量) · 3N(座標) [ミクロ的]
P: 位相空間内の1点 ______↑ τを無限にすると
仮定: 位相空間が2つの不変部分に分解出来ない 閑話休題: ウィルソンの霧箱 Wilson cloud chamber: 粒子飛跡を検出する基礎的装置 Wilson (英, 1869-1959): 1987 基礎原理発見, 1911 実用装置完成
容器中に水蒸気を飽和させた清浄空気入れる → ピストン素早く引く → 容器体積膨張 → 温度↓ → 水蒸気過飽和状態 → 中に荷電粒子飛び込みイオン形成 → イオンに沿い水滴凝結し飛跡可視 (撮影可 - 飛跡見えるよう側面から光当てたりする) 霧箱を磁場中に置く → 荷電粒子軌道曲がる → 曲率curvature半径等測定し粒子に関する情報得る 現在は泡箱・放電箱主流 - 教育目的以外稀(歴史的重要性) 放電箱 spark chamber 泡箱 buble chamber: 液体を過熱状態にし荷電粒子通過により小泡を作り素粒子・放射線飛跡観察に使う
電子ビーム(電子線) electron beam 原子核の構造
核子数 n, p, t → 3H, [τ, h] → 3He, α → 4He, d → 2H Λ, Σ: バリオン(重粒子 現在不使用) baryon (barys = Gr 重い) 電子散乱電子が原子・原子核・素粒子等の影響で運動のエネルギー・方向が変わること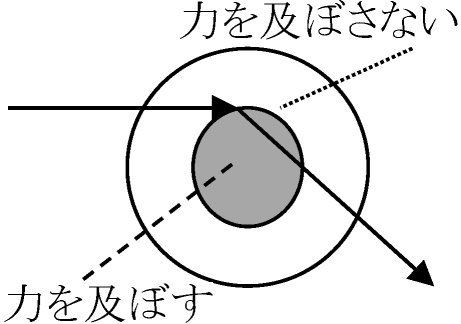
原子 ~10-8Å, 原子核 ~10-13 - 10-12 fm (fm = 10-13 cm) 電子が原子核の中を通る時
原子核の中心付近: 受けるクローン力弱
表わす記号: n = 軌道運動 En = E l = 回転運動 → τ = 角運動量 He原子電子が受ける作用 → He原子の基底状態で1つの電子の感じるポテンシャル第1イオン化ポテンシャル -25 eV (cf. H: -13.59 eV ほぼ2倍)
場所によりチャージ変化のあるポテンシャルと考えられる |
Li原子の第一イオンポテンシャル = -5 eV ← 水素よりやや低くなってしかるべき Na原子l = 0, 1, 2, 3に対するNa原子のE準位
原子スペクトル全原子の[水素原子を基準とした]E状態原子から電子を1個取り出すE → 0Eより低い所にあるか Def. 第1イオン化E, E1: 1番高状態にある1電子を取り出すE Def. 第nイオン化E, En:それまでに(n - 1)個の電子がとり出されており、n番目に電子を1つ取り出すE 同じ原子であればnが大きいほど高いE (Na+はできてもNa2+はなかなかできない) _________元素の第一イオン化ポテンシャル (y = ΔE1/eV)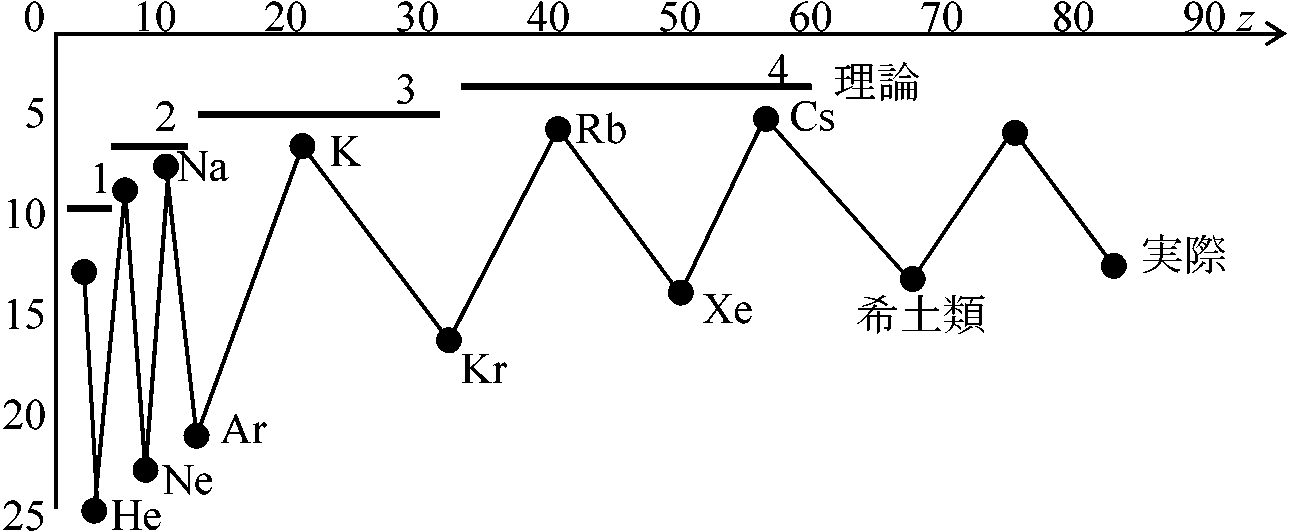 実際と食い違う = He: 2個のチャージ(単位チャージの2倍) → 低すぎる Heが1個の電子の感じるポテンシャルが「場所によりチャージが変化する様なポテンシャル」のように考えられる原因 = 極めて遠くではHのクーロンポテンシャルと同じ。極めて近くではHeのクーロンポテンシャルと同じ ⇒ 全体としてその中間的値に確率分布 → -e2/r·f(r)
i) r » a: f(r) = 1 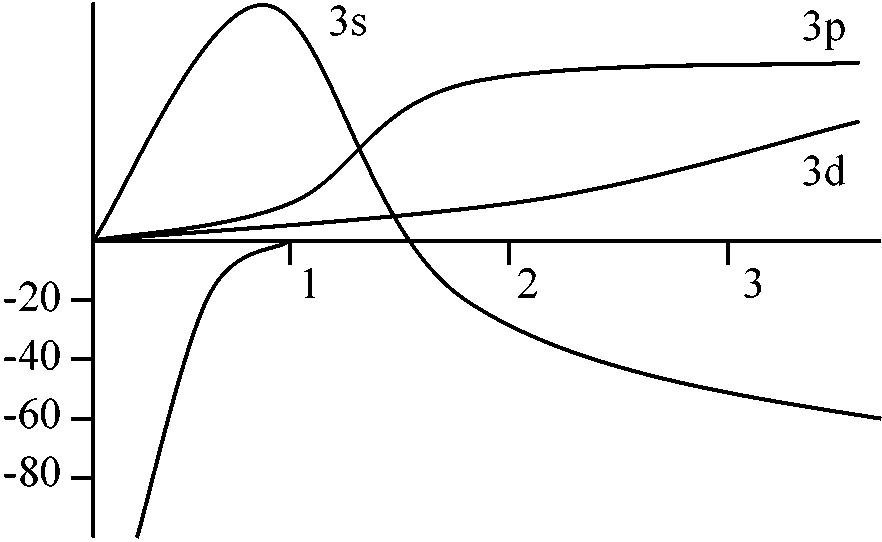 水素原子の3s, 3p, 3dの波動関数 矛盾が出たらやり直す → SCM (self consistent method) Na原子のE準位
R = 1.0~1.2 × A1/3 fm (1.1 × A1/3 fm)
rp = 0.085 ± 0.11 fm ⇒ 正分布 = 0.62 φm (隣の核子までの距離 = 1.85 φm) 分子moleculeと原子核(核) nucleus (pl. nuclei)
水素のスペクトル線グループ(他にもある)
バルマー系列 Balmer series
リッツ結合則 Ritz combination principle考案 空間の回転とスピノールスピンの自由度 degree of freedom on spin異常ゼーマン効果 Zeeman effect: 電場をかけたとき原子スペクトルが偶数本に分岐
→ 電子はスピン1/2の粒子 → 2つのスピン成分(sz = ± 1/2)を持つ [2成分複素ベクトル ≡ スピノール] 反陽子の科学⇒ 共存不可能 = 直ちに消滅粒子 particle vs 反粒子 antiparticle
陽子 vs 反陽子anti-proton 質量がゼロか電子の質量以下の中性粒子
物質 matter vs 反物質 anti-matter ↔ 対消滅 pair annihilation: 粒子と反粒子が衝突しEないし他粒子に変換される現象 |
|
慣性(座標)系: O-XYZ :=> 静止系 O'-X'Y'Z' := 運動系(各座標軸が静止系に常に平行に運動する座標)
dx/dt = dx0/dt + dx'/dt 静止系に対するP点の速度 ⇒ (dx'/dt, dy'/dt, dz'/dt) ≡ 相対速度 relative velocity運動系に対するP点の速度 ⇒ (dx0/dt, dy0/dt, dz0/dt) ≡ 変換速度transformed velocity運動系の静止系に対する速度 絶対加速度 absolute acceleration (d2x/dt2, d2y/dt2, d2z/dt2)相対加速度 reltaive acceleration (d2x'/dt2, d2y'/dt2, d2z'/dt2) 変換加速度 transformed acceleration (d2x0/dt2, d2y0/dt2, d2z0/dt2) Galilei-Newton の相対性原理 (不変性 form invariance)F(X, Y, Z): 質量mの質点に働く力(静止系)→ m·d2x/dt2 = X, m·d2y/dt2 = Y, m·d2z/dt2 = Z ∴ m·d2x'/dt2 = X – m·d2x0/dt2__m·d2y'/dt2 = Y – m·d2y0/dt2 __m·d2z'/dt2 = Z – m·d2z0/dt2 運動系が静止系に対して運動しているために –m·d2x0/dt2, –m·d2y0/dt2, –m·d2z0/dt2は現れる → 力ではない→ d2x0/dt2 = d2y0/dt2 = d2z0/dt2 = 0以外で運動法則成り立たない ⇒ 慣性系に対し等速度で進む(加速度持たない)座標系 = 慣性系 ⇒ 互いに一様な速度で移動する全ての系⇒ 物理学の基本法則は同じ(ガリレイ) 問題: 絶対静止した空間に固定した座標系は定められるか エーテル ehterPrinciple: ホイヘンスの原理 Huygens' principle= 光波動基本原理 = 波動説 ⇔ 粒子説 (Newton): 光は微小粒子 → 光反射説明可能、屈折説明不可能
(Huygens, Christian 1629-1695, 蘭: 数学・天文・物理。ホイヘンス接眼鏡は彼の名) 波動説支持(ホイヘンス説復活) ヤングの干渉実験 Young's experiment for interference
スリットslit用いた光の干渉性を示す実験
偏光 polarization (polarized light)発見 偏光角(ブルースター角) polarization angle (polarizing angle, angle of polarization, or Brewster angle) 1822 Fresnel, Augustin Jean 1788-1827, 仏
周波数・振動数単位フレネルは彼の名
天文・物理・政治家(パリ理工科学校教授、パリ天文台長) Foucault, Jean B.L. 1819-1868: 光が波動であることを実験で示す ⇒ 横波: 弾性体中で発生 ⇒ エーテルは弾性体である必要1873 Maxwell, James Clerk 1831-1879, スコットランド
数学的に電磁気現象が波動を生じることを示す → 電磁気現象はエーテル中の電場磁場振動(電磁波)
Michelson, Albert A. 1852-1931: 1881 光干渉を用い、エーテルに対する地球の速さを求める(失敗)
GM1 = GM2 = l
GM1: 地球の運動方向
= 2l/c·(1/√(1 – v2/c2) – 1)
始めGM1を地球の運動方向に一致させる → 直角に回転させGM2を地球の運動方向に一致させる
→ 縞は波長の1/3ずれる エーテルに対する速さ = 恒星に対する速さ(30 km/sedc) 実験値: < 0.02 ⇒ 地球がエーテルに対し運動している証拠なし 1888 Hertz, Heinrich Rudolph 1857-1894, 独
光波 = 電磁波 → エーテルは弾性体と考える必要ない = Lorentz-Fitz Gerald contraction (両名が独立に発見)
Fitz Gerald, George F 1851-1901
v: 速度, c: 光速度 ⇒ エーテルに対しvで動く物体は、その方向に(1 - v2/c2)1/2の割合で短くなる ローレンツ変換Lorentz transformation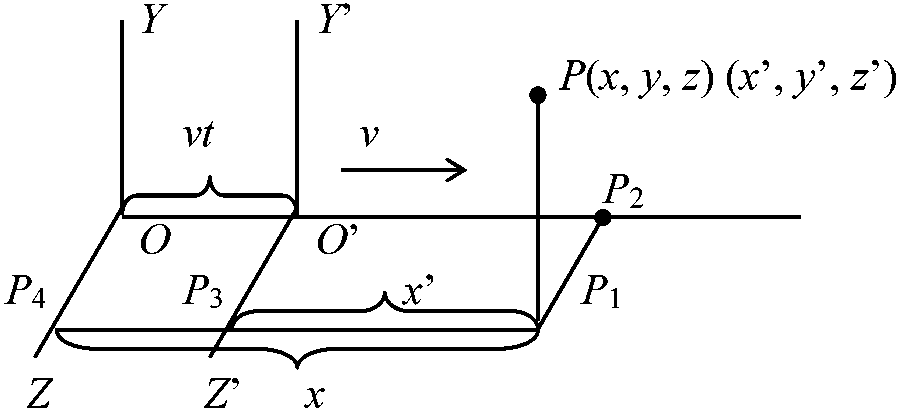
静止系(O–XYZ, t)
x' = (x – vt)/√(1 – v2/c2) 特殊相対性理論 theory of special relativity= 特殊相対性原理 principle of special relativity1905 Einstein A 1879-1955, 独: 特殊相対性理論
= エーテル存在否定 → 空間自体に光を伝える性質存在
1) 等速直線運動をする系では、全ての物理法則が同じ形で成立 ↔ 非相対論 non-relativistc theory ⇒ 光速(度)不変の原理 principle of constancy of light velocity
互いに等速直線運動をする観測者に対し、光はあらゆる方向に同一の速さで伝わる |
空間と時間 (現代原子論)同時性Ex. 静止系上の2点P1(x1, y1, z1), P2(x2, y2, z2)
━━━━> v → 運動系で観測した2現象の時刻をt1', t2'とする
t1' = 1/√(1 – v2/c2)·(t – v/c2·x1) ≡ [絶対時間は存在しない] 時間の遅れ time-lag (time dilation)Ex. 静止系に対し速度vで運動する座標系上の点P(x')で起こる現象の経過時間を測定t = 1/√(1 – v2/c2)·(t' + v/c2·x') t1: 運動系から観測, t2: 静止系から観測 t1 = 1/√(1 – v2/c2)·(t'1 + v/c2·x'), t2 = 1/√(1 – v2/c2)·(t'2 + v/c2·x') 静止系で測られる現象の時間の長さ, T = t2 – t1 = 1/√(1 – v2/c2)·(t2' – t1') ∴ t2 – t1 > t'2 – t'1 長さの短縮(収縮) length contraction長さlの物体が速度vで運動長さ: 両端が同時に占める位置の間の距離 → 長さは物体の運動速度によって異なる測定がされる 物質と共に運動している座標系からみて時刻t'に物質の両端が占める座標x'1, x'2 → l' = x'2 – x'1 t'に対応する静止形の時刻tにおける物質の両端の座標 → l = x2 – x1[Lorentz変換] x1' = 1/√(1 – v2/c2) × (x1 – vt), x2' = 1/√(1 – v2/c2) × (x2 – vt) x2' – x1' = 1/√(1 – v2/c2) × (x2 – x1) ∴ l' = 1/√(1 – v2/c2) × l ⇒ l' > l 速度変換 conversion静止系と運動系から観測した速度の間の関係
[Lorentz変換] → dx'/dt' = u, dy'/dt' = 0, dz'/dt' = 0 これを静止系から見る → dx/dt = (u + v)/(1 + v/c2·u), dy/dt = 0, dz/dt = 0
Case. u = c → dx/dt = (c + v)/(1 + v/c) = c ⇒ 光速に光速が加わっても光速 相対論的質量 relative mass→ 質量変化静止質量 rest mass, m0: 観測者に対し静止しているときの物体の質量 物体が観測者に対し速度vで運動したときの質量, mv → mv = m0/√(1 – v2/c2) エネルギー・質量保存則 law of conservation of energy and mass= 質量・エネルギー保存則 law of conservation of mass and energy⇒ 質量・エネルギー変換 mass-energy conversion 質量・エネルギー方程式 mass-energy equivalence Def. T: 運動している物体の運動E= 静止状態から運動状態になる際になされた仕事 T = mvc2 – m0c2, or E (全E) = mvc2 = T + m0c2
⇒ 運動している物体のEが運動による質量増加に光速の2倍をかけたものに等しい Def. 結合E binding eneryg = 質量欠損 mass defect: 陽子-中性子結合後に減少した質量 ⇒ 運動量, p = m0v√(1 – v2/c2)m0: 静止質量 → 速度の1乗に比例しない 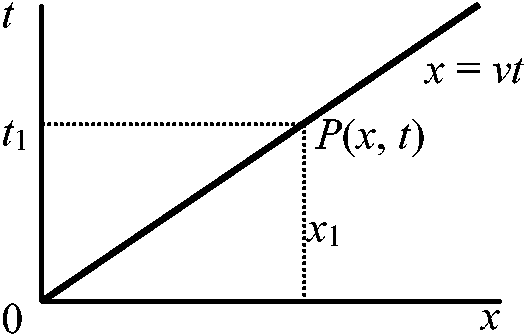 1908 Minkkowski Hermann (1864-1909)
1908 Minkkowski Hermann (1864-1909)
相対性理論を空間と時間の4次元の幾何学として展開(4次元の世界)
直線上をvで運動
光速 c: OP2 = x12 – c2t2 ⇒ 時間と空間は別々に存在するのではない = 4次元の時空世界 一般相対性理論 theory of general relativity= 一般相対性原理 principle of general relativity (Einstein 1916)特殊相対性理論: 等速度系 → 一般相対性理論: 加速度系[拡張] → 重力場があれば空間は曲がる = Riemann幾何学を応用 測地線 geodesic line: Riemann幾何学における2点間の最短距離 – Euclid幾何学の直線と同等
力の作用を受けない質点の軌道は測地線になる Ex. 1. 近日点 pelihelionの移動 ↔ 遠日点 aphelion Ex. 2. 赤方偏移red shift ↔ ブルーシフト(青方偏位) blue shift: 近づく光源からの光が短波長側へずれること 光 light (光線 ray)古典力学で波動性と粒子性は両立しない波動 = 媒質中で伝わる振動 ⇔ 粒子 = 決まった質量を持つ物体 1) 光の光線モデル ray model of light = E粒子束(量子力学)
回折・干渉・偏光をうまく説明 c: 真空中の光速度 v: 1秒間の振動数 λ (cm) nm = c/cm
nm: 媒質mの屈折率 cm: 媒質m中の光速度 Ex. ray = 555 nm, ダイアモンド, nm = 2.42 → 2.42 = (30 × 1010)/cm ∴ cm = 1.22 × 1010 cm/sec 1) 電磁場の変化: 波動 → 電磁波としての扱い ⇒ 光 = 電磁波⇒ 光の二重性: 排他的なものではなく共存可能 光は空間を波として伝わり、物質によって放出・吸収される時は粒子として振舞う Def. 干渉 interference: 光(電磁波)ぶつかる→ 力増constructive減destructiveさせる現象
(可)干渉性 coherence チェレンコフ放射 Cherenkov radiation屈折率nの媒質中: 光速 = c/n (c, 真空中光速)
Def. 衝撃波 shock wave (sonic boom) = チェレンコフ放射(-光)
放出角度は衝撃波の波面が荷電粒子の進行方向となす角を θ
γ線等が大気中で起こすシャワー中の粒子も殆ど元の粒子の方向に走る ↔ 相手が重いと相手に余りE与えず自分が飛ばされ方向を変えるだけ 時間とは何か(相対性理論より)時空 spacetimeと物質 matterの運動
時間: 外から与えられたものではなく研究対象 = 時間の進み方は運動状態により決まる → 時間は変化 |
|
= 統一理論 unified force theory: 統一の力(4つの力) universal force = 万物の理論 → [候補] 超弦理論(超紐理論) Newton: 天体の力と地上の力を万有引力として統一 = 重力場 Maxwell: 電気力と磁気力を電磁気力として統一 = 電磁場 Einstein: 重力場と電磁場は同じ空間の性質として統一 = 統一場
_______ 力の種類__力の伝達粒子__力の大きさ(目安)
1. 重力 gravity全素粒子に引力(万有引力)として働く = マクロ世界支配重力子(グラビトン) graviton: 質量なし → 重力子の交換で伝播 (重力 = 重力子の交換) → 無限遠に届く E = mc2 (重力 ∝ 質量, 質量 = エネルギー) → 重力は全粒子に働く
素粒子質量は非常に小さく、加速器で到達できるエネルギーでは素粒子間重力は無視できる 2. 電磁力(電磁気力) electromagnetic force日常経験する重力以外の全ての力は電磁気力Ex. 電子と原子核を結びつけ原子を作る力、原子同士を結びつけ分子を作る力 光子 photon: 質量なし → (電磁気力 = 光子の交換) → 無限遠に届く電磁気力 ∝ 電荷
電荷を持った粒子: 光子(仮想光子)をお手玉しながら走る = 電荷粒子は光子の衣をまとう |
3. 弱い力 weak force短距離間でのみ働く。通常、電磁気力より遥かに弱 → 全クォーク・レプトンに働く原子核β崩壊、中性子、π中間子等の粒子崩壊の力 = ミクロの世界で重要 弱い力を媒介する力の粒子: W, Z粒子 = 大きな質量 → 弱い力 = W, Z粒子の交換 結合定数は電磁気力と同程度/力が届く距離非常に短い = 力の見かけの強さ弱い → 日常感じない(核に働く)弱い相互作用 weak (nuclear) interaction 2 + 3 = 電弱力 ⇒ 電弱理論 electroweak theory
ボース粒子(ボソン)Bose particle, or boson: ボース統計に従う粒子
ヒッグス場との相互作用なければ、これらの力の粒子の運ぶ力は元々は同じ
⇒ 光子の伝える電磁気力と、WやZが伝える弱い力は電弱力として統一 4. 強い力 strong force電磁気力の100倍程の大きさを持つ最も強い力強い相互作用 strong interaction (核に働く強い相互作用 strong nuclear interaction) 強い力: 全カラー荷を持つ素粒子に働く = グルオンの交換 クォークを結びつけ、陽子(p)や中性子(n)を作り、また陽子同士の間に働く電気的な斥力に打ち勝ち、中性子と共に原子核を作る 強い力 ∝ カラー荷: クォークのカラー荷 = 赤青緑3原色(仮想)
強い力を媒介する力の粒子グルオンは白を除く色の組合せ: 3 (赤・青・緑) × 3 (反赤・反青・反緑) - 1(白) = 8 → 8種類: いずれも質量持たない |
[ 論理学 ]
方法 method主題 → 方法 (方法が先行することはない: データ氾濫、理論は貧困)事実判断 → 因果関係 → 価値判断 (哲学) 斉一性 uniformity (Mill 「論理学体系」) =
自然は同じ事情(基礎条件postulate)のもとでは同じ現象を起こす 科学的説明Braithwaite 1953証明 demonstration, 演示 illustration, demonstration → 認識論 epistemology 第1段階: 経験的事実fを証明する
gであるからという説明 → 因果的説明 法則L1, L2など(より一般的な法則の場合が多い)で説明する 科学的方法 (scientific method)1. 事実→ データ収集A. 観察 observation現象 phenomena を感覚器官により正確に経験する |
B. 実験 experiment制御実験 controlled experiment: 現象が複雑な因子・条件下で起こる → 因子を単純化(か除去)
操作変数(操作可能変数) manipulated variable Ex. 温度一定下で光条件を変え植物成長測定 2. 概括(一般化) generalization→ 帰納法: 検証 verification に耐えうるものでなければならないa) (科学的)法則 scientific law (natural law)個別法則 < 一般法則法則 → 因果性(因果律 law of causality)
実験的に得た法則 → 定式化 Ex. 質量作用の法則基礎, Hessの法則 b) 共通事項表記(科学的表記) scientific notation3. 予測(予知) prediction普遍的 universal, 必然的 necessary導出量(推定量) derived quantity: 結論を論理的に導き出した量 Ex. ハレー彗星(Halley Edmund 1656-1742): 1531, 1607, 1682年出現彗星同一 → 1758年回帰と予測 探索的研究 exploratory research明確に定義されない問題を調査する研究 (≠ 検証的研究) |
|
作業仮説 working hypothesis: 因果関係について立てられる仮定 → 推論に基づく → 観察(結果)と解釈、推論と仮説は区別される 説 theory: 仮説に基づく学説 → 検証可能性がある 法則 law (理論 theory): 検証に耐えたもの(Popper 1965) 直感 intuition (≈ ひらめき): 仮説・理論誕生に重要な要因であるが、思考としての直感過程は不明の点多 概念モデル mental model: 対象を直接知れないとき、間接的方法で情報を集め、解釈し組み立てられたモデル 形式モデル: 概念モデルの中で図式化、数式化されたもの Ex. 原子模型
研究対象 ___ モデル |
AとBの関係に対応する関係が = A'とB'の間に成り立つ 図. モデルによる類推(類比, アナロジー): 上下両様の表し方がある 仮説検証
(八杉 1979) |
[ 哲学者 ]
|
1. 宇宙や人生の根本問題を理性的思弁で突き止める学問 Ex. スコラ哲学
哲理 philosophical principles: 哲学上の学理 (s.s. 特に人生・世界の本質を見通す道理) 2. 自分自身の経験から築き上げた人生観(世界観) Ex. 人生哲学
人間は常に行為する Ex. 寝ている → 行為 ☛ Sartre Ex. 「基本的人権 fundamental human rights」とは何か ☛ 幸福論 イデオロギー(思想形態・観念形態・意識体系) ideology定義・概念は変遷
Ex. イデオロギー闘争: 社会階級間イデオロギー相違に基づく闘争(マルクス・レーニン主義) ギリシア哲学唯物的で個人主義的な3(4)学派誕生1) キュニコス学派 (→ ストア派に発展) 善 ≠ 外的 → 善 = 魂の内部に存在 → ストア学派倫理学の原理 2) ストア学派 Stoicism: ヘレニズム時代創設の古代ギリシア哲学学派起源: ソクラテス弟子アンティステネス創設のキュニコス学派 第1期(BC300-BC200): BC300年頃キプロスのゼノンによりアテネで創設キュニコス学派のソクラテスに学ぶゼノンが彩色柱廊で知られたストア(柱廊)に学校開設したのが始まり (学派名称も同由来) 第2代学頭クレアンテス著「ゼウス賛歌」断片現存: 最高神は全能唯一神にして道徳的統治者と記述 クレアンテス後継者はクリュシッポスで、これら3人が代表者 第2期(BC200-BC50): ストア学派哲学普及し、ローマにも知られる パナイティオス: ストア学派を本格的にローマに伝えた ポセイドニオス: パナイティオスの弟子。ローマの有名な演説家キケロの教師 |
第3期(ローマ時代) キリスト教がローマ帝国国教になった後も勢力を持ち続け影響はルネサンス期(Renaissance)まで及ぶ
共和制末期: 小カトーは優れたストア哲学者 思想ヘレニズム期他学派同様、倫理学に関心 → 幸福が人々の最大関心事特徴: 倫理学を固めるため、論理学・自然学の理論開拓 → 概念・判断・推論の理論としての論理学はストア学派が骨格形成 Ex. 仮言三段論法発見 自然学世界は物質からなるが、物質そのものは受動的 → 別に世界を動かし世界に秩序を与える能動的原理(ロゴス)存在 = 神の理性であると共に、ある種の微細な物質とも考えられ、「息」「火」とも呼び、ヘラクレイトスは宇宙の根源とした魂 = ロゴスの現れロゴスに従い生きる = 神が定めた世界(自然)秩序に従う(人間の務め)「自然に従い生きる」は、自然法思想展開で決定的 → ローマ法に甚大な影響 魂の内的状態 = 思慮(自制心)日常生活で心をかき乱すものは情念や欲求であって、こうしたものから解放され不動心(アパテイア)を得るために必要なものが思慮や自制心コスモポリタニズムストア学派1特徴: どの人間も唯一の普遍的な神の現れ → 人間同士の付合い → 社会的地位、貧富、民族の違い等外的なものは全く意味なく、万人は等しくコスモス(世界)市民であるキリスト教誕生前 = 全人類は生まれつき平等 ⇒ 兄弟の様に愛しあう必然性 ギリシア哲学(中近世)形而上学 metaphysics: 現象を先見的原理で説明し実在realityの真相得る3) エピクロス学派(Epikouros): 快楽主義 ↔ 自制重んじるストア学派と対立(stoic = 「禁欲的」の意味加わる) 4) 懐疑主義 skepticism: 物事の存在・価値等を否定ヒトが普遍的真理を捉えることは不可能 |
|
キリスト教に従うギリシア哲学 – 数学・経験重視しない トマス・アクィナス神学: キリスト教啓示の超自然的内容を自然的人間理性(アリストテレス哲学と科学)から理解しようとした哲学的・神学的運動 → スコラ学: 「神は唯一全能創造主」、「魂不滅」という信念 スコラ学という用語1) この時代の思想に特有な学習への精神や方法だとか、他の時代の同じような精神や態度 2) スコラ学者 = 修道院・大聖堂付属学院長(初期) → 学院が大学化し学院・大学で哲学・神学を教える人(後) 欧州キリスト教修道院付属学院・大学で11c紀半-15c紀半まで支配的最終的理想 = ギリシア・ローマ自然的知識とキリスト教宗教的知恵を、秩序だてた体系に統合
目的: 哲学・神学で様々な教義広く展開 → 運動全体を統一要因 = 共通目的・態度・方法 理性と啓示は神を知の源 → 真理 = 神の主要属性 → 理性-啓示間で神が自己矛盾しえない 啓示-理性間に対立 → 理性を誤用か、啓示という語を不正確に解釈した スコラ学者達: 啓示は神の直接の教えとし、自然的理性より程度の高い真理と確実性を啓示に認める
→ 宗教的信仰-哲学的理性間のみかけ上の争い → 信仰が優勢な審判者 = 神学者の判定は哲学者の判定をしりぞけた
哲学もイスラム神学も真理に近づける ↔ 真理到達は哲学のみ 初期 Ex. 聖職者アンセルムス(伊): 2能力を明確に区別しない 理性が啓示を証明できると自惚れてもいない 最盛期 Ex. 神学者トマス・アクィナス(伊): 理性と啓示の均衡を完成トマス以降 Ex. 神学者ドゥンス・スコトゥス(スコットランド, 先駆): 理性により証明可能な真理領域を制限
哲学で証明された教義は、信仰に基づいてのみ受け入れた 大家 = ギリシア、ローマの偉大な哲学者 + 初期の教父 アリストテレス = 哲学第一人者 → 「哲学者」 = アリストテレス 初期キリスト教聖職者(神学者)アウグスティヌスが、聖書と教会の公会議を除けば神学第1権威 大抵のスコラ学者は、アリストテレス経験科学見解を無批判に受け入れ、その権威に執着 → スコラ学の弱点 → ルネサンス期以後の科学者達がスコラ学を軽蔑拒絶する要因 中世スコラ学: 古代著者の研究のみを通じ考え著述するよう教育される(古代文化思想は中世より豊か) |
[批判] 思想成熟し独創的哲学的著作も生まれ独自に思想形成されても、見解に威信を与えるため古典引用止めず、古典を編集反復しただけ(トマスやスコトゥス等も古代テキストに従順依存的) 時に古代テキストと自分の立場を調和させようと古代思想家達の意図にそぐわぬ解釈 → 注釈者本人の意見表明前後に、単なる文体上の装飾とし古典を出したり、引用で注釈者見解は過去からのもので新奇でないと思わせる効果 → スコラ学者は慎重で、思想の独創性を求めない 方法・注釈: 1) アリストテレスの論理学と哲学用語を用い教育、論証、議論 2) 古典を教えるに当って承認された権威者による注釈を用いる 哲学: 古典は大抵アリストテレス / 神学: 主テキスト = 聖書 + 「命題論集」 命題論集: 12世紀、神学者ペトロス・ロンバルドゥス(伊)がまとめた、初期教父達の神学問題意見集
初期スコラ学者は、注釈テキストに従う
中世大学教授: 教授団と学生の前で挑戦者全員の攻撃から自分の教えを弁護 – 1年に数回課した 13 c (スコラ学全盛期)
ドミニコ会: トマス・アクィナス 実験的方法重視 → 経験科学 scientia experimentalis
イタリアの神学者: ナベントゥラ、ドゥンス・スコトゥス Occam ,1285(6)-1347(9) 英, スコラ学者(唯名論・哲学・論理学)
スコラ学哲学体系を全面的に攻撃: 自然的理性と哲学の領域はスコラ学者が考えるより制限される = 「けちの原理」単純さの原理) ⇒ モデル選択 「むやみに実体の数を増やすな」「2つの理論がある時は、真偽を明らかにできる証拠が新たに挙がるまで一番単純な理論用いよ」 → 思考節約原理
Ex. 「石を投げたら地面に落ちる」 → 「地面に落ちるか、上に落ちたり、左に行く」と複雑理論も立つ: 1879 教皇レオ13世: 大規模にスコラ学再興試みる – 13世紀スコラ学(トマス)体系を時代に即し再考
スコラ体系改革に近代思想の真の功績を結びつけるため |
|
Spinoza, Benedictus (Baruch) De (スピノザ, 蘭) 1632-1677 合理主義: 基本は形而上学的 Leibniz, Gottfried Wilhelm (ライプニッツ, 独) 1646-1716 哲学・数学、国政・外交等実務でも活躍 モナド論(形而上学説): モナド(単子) = 万物構成する不可分不滅の実体 モナド間相互作用なし - 神(最高モナド)に立てられた予定調和を表現 イギリス経験主義哲学 (イギリス経験論 British empiricism)全ての知識は経験に由来するBacon, Francis (ベーコン, 英) 1561-1626 (Roger Baconとは系譜関係なし) 近代哲学誕生 = 帰納・演繹 ⇒ 自然法則を知る手法 = 帰納法 + 実験 実験は確実な経験に到達させる – 魔術から科学へ 「大いなる再興」(6部作予定だが未完) 2部「新機関Novum Organum」(1620) – Organonに対抗 – 帰納法の表れ 科学 = 史学 + 詩学 + 理学 人間幸福を進める(神に背くものではなく神を敬う道) → 産業の新発展期の考え方代表 技術: 隣人への愛を実現する手段であり神意にかなうもの人間: 自然を支配し、同胞の幸福のために努力する反面、自然に従う 知識 力であり信頼を置く Locke, John (ロック, 英),1632-1704 経験主義(懐疑主義) = 近代哲学認識論確立 経験主義: 因果律 law of causality → 生得的観念存在しない – デカルトの主張否定 心: 理性・知識・観念全て感覚に基づく経験により獲得 → 因果関係 懐疑主義: 懐疑から出発し認識の本性を分析Hume, David (ヒューム, 英) 1711-1776: 経験主義 + 懐疑主義 因果性 = 習慣による期待 Ex. Aが起ると(いつも起こる)Bが起ること期待 ↔ idealism フランス唯物論哲学 (French materialism)Bruno, Giordano (ブルーノ, 伊) 1548-1600: コペルニクス地動説支持(火刑)Descartes (デカルト, 仏) 1596-1650: 思考の合理性 真実(= 一般原理): 全てを疑い、その後に残る明晰(≠ 曖昧)で(紛糾していない)判明なもの 我思う、故に我あり → 懐疑主義の表れ 「方法序説」(1637), 生命機械論(機械論・機械原因論) 波動説: 力学的宇宙系(渦動論)提案 → Newtonにより否定 ドイツ観念論哲学(カント哲学) (idealism)Kant 1724-1804 → 新カント哲学(西南ドイツ学派、マールブルク学派) |
Windelband W. 1848-1915, 独 / Rickert H. 1863-1936, 独 自然現象 = 再現可能性(反復可能性) → 法則定立学 社会現象 = 一回性(反復不可能性) → 個性記述学(文化科学) Hegel Georg Wilhelm Friedrich (ヘーゲル, 独) 1770-1831 弁証法 観念論(唯心論)→ 唯物論 Marx – Engels 米国実用主義哲学(プラグマティズム)米国が欧州と区別される独自思想、文化を持ちたい願望の表現 + ダーウィン進化論概念や法則の実用性 = 方法の基準 Dewey John (デューイ, 米) 1859-1952 プラグマティズム → 概念道具説: 概念も環境への適応活動の道具 図. 20世紀以降の哲学の動向 __1960年代まで____________現代 [マルクス主義 (独)] ⇒ フランクフルト学派_ 解釈学 [ 実存主義 (仏)]___⇒ 現象学__________構造主義 ⇒ ポスト構造主義 [ 分析哲学 (米・英)] ⇒ ⇒ ⇒ ⇒ ⇒ ⇒ ⇒ ⇒ ⇒ ⇒ ⇒
分析哲学: 記号論理、概念分析、数学・自然科学の哲学を扱う(英語圏主流哲学スタイル マルクス主義 (Marxism)政治経済思想 = 科学的社会主義Marx K (マルクス) 1818-1883, 独: 弁証法的唯物論 Engels F (エンゲルス) 1820-1895, 独: 弁証法的唯物論 自然科学世界は弁証法的発展を示す 西洋社会を階級闘争の観点からとらえ、資本主義によるブルジョアの搾取から社会主義体制を経て共産主義に移行することが不可避であるとするもの 上部構造: 物質的・経済的構造に支えられた観念やイデオロギー 1883 Engels 「空想から科学へ」
社会主義思想 1909 「唯物論と経済批判」 - マッハ、アベナリウスの思想を批判 |
1)言語の恣意性と差異化言語学 linguistics = 音韻論 (音組織) + 統語論 (≈ 文法) + 意味論ソシュール Ferdinand de Saussure (1857-1913): 言語学 1916 一般言語学講義 言語 = 時代で変化 ↔ 言語が言語である限り不変で共通した構造存在
→ それまでの言語学は言語の歴史的変化(通時態)のみ考えた
Ex. 英語: 年上・年下区別なく"brother"と表現 → 日本語: 年功序列思想浸透し「兄」と「弟」区別 = 言語の恣意性: 区別の仕方は言語体系により様々であり絶対的決まりなし 言語発音も「区別」だけ存在 – 「区別」もその言語体系により変化 = 「恣意的」 Ex. 日本語: r, l発音区別なし ↔ 英語: 区別必要 Ex. rice vs lice 言語(記号、シーニュ): 結びついて言語は言語とし機能 = やはり「恣意的」
= 「シニフィエ (signifie 意味内容、所記)」: それが指す意味内容 2)音韻論言語成立する「音」法則 – ソシュールの言語「差異化」(と恣意性)から発達音素: 単語発声時にその単語が成立する最小単位の音 = 音韻論の重要鍵 Ex. 日本語: 「リンゴ」 → 音素「リ」「ン」「ゴ」 発音者により音の周波数と長さ違う → 音素は物理学的に定義できなかった。ここでソシュール思想活かされる ⇒ 音素も「差異化」でしか認識できない。この音素は個々の言語体系により「恣意的」音素研究 (Jacobson): 音素 = 個々の言語体系により異 → 個々の音素を差異化する「対立軸」は共通 Ex. pとbの違い: 「無声音」「有声音」 → 全音素差異化は「2項対立」 音素差異化する際の弁別特性を12対発見(「母音・非母音」「鼻音・非鼻音」等)重要な対立項や、人が初めに話せる音を考え、彼は「母音の三角形」と「子音の三角形」見出した
人が初めに話せる音 = 母音a, i, u、子音p, t, k → 音素区別する2項対立は,「密」と「疎」,「鋭」と「鈍」の2組 Ex. "p/t"は「鈍/鋭」で区別され、この中間に"k"は位置する。更に、p(or t)/kの区別は「疎/密」でなされ、pとtは同程度に「疎」である。「母音の三角形」も同様 3) 構造主義の発展a) 機能主義人類学歴史主義 (伝播主義) (ソシュール登場までの言語学): 言語がその歴史における変化等を研究する歴史主義進化論の影響: 言語学や人類学に見られ、同一のある習慣とか文化が複数の場所で見つかると、伝播経路や、原住民社会と西欧近代社会の比較が行われた。Ex. フレイザー『金枝篇』 機能主義人類学: 習慣なり何なりの、その社会における機能(有用性)を重視現地調査(field work)重視 - ソシュール: 歴史主義捨て言語の「共時態」重視
問題: 多くの社会に「インセスト・タブー」(近親相姦禁忌)存在 → 遺伝的劣化避けるため「インセスト・タブー」集団残る = 適者生存で説明 b) 構造主義 structuralismLevi-Strauss, Claude (1955): 機能主義だけでは全てを説明できないモース M, 仏, 人類学: ニューギニア島付近の風習「クラ交換」に興味
ある部族がその部族の「宝物」を別部族に贈る → 贈られた部族はまた別部族に贈物 Ex. 「近代」社会貨幣: 貨幣そのもの ≠ 価値 ⇒ 物と交換可 = 価値 社会を「交換のシステム」という観点で見直す = このシステムを「全体的社会的給付」という |
Levi-Strauss: モース「贈与論」観点から「未開」社会における婚姻見直す
同親族内結婚 = 他グループに女性を贈与できず交換物価値がなくなる → インセスト・タブー発生 Ex. 女性を「贈物」と捉えると、婚姻は女性の「交換」に対応 親族問題: ヤコブソンの「二項対立」原理を用いる Ex. 女性を男性が接近することが出来る他の婚姻グループの女性(妻Wife 略語W)と男性が接近できない同一婚姻グループである女性(姉妹: 略語は息子Son と区別するためZ)に差異化
「妻」、「姉妹」の範囲は社会で異なり「恣意的」 ⇔ 「W/Z」対立は普遍的 c) 神話学Levi-Strauss: 人間精神の隠れた「構造」を知るため親族研究から人間精神産物の「神話」に興味移す注目したのは神話の「筋」ではなく、その神話を構成する「要素」
一見荒唐無稽な神話、他部族間で類似した筋、結末逆転する神話も、表層にとらわれず「構造」を見る → 構造主義ではテキストを「分解、解体」し、その底に流れる無意識の「構造」を読み取ろうとする
構造抽出法に数学利用(神話を「要素」に分解するアイデアはヤコブソンの音韻論からだが、その要素が「変換群」によって置換されて様々なバリアントが出来上がると考えた)
Ex. 非ユークリッド幾何学: 「ユークリッド幾何学」で「自明」な「公理」を別公理で置き換えても矛盾しない d) 近代的世界観崩壊Levi-Straussの親族研究や神話学(ミトロジーク)は「理性重視」、「歴史進歩主義」的思想に衝撃与えた
ヘーゲル・マルクス: 人間の理性は歴史が進むにつれ「進化」 図. 「言語論的」転回とは 17世紀 ⇒⇒⇒⇒⇒ 20世紀 ⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒ 21世紀 認識論的転回_____言語論的転回_________________? (意識を分析)______(言語を分析) ___________________分析哲学 ___________________構造主義・ポスト構造主義 ___________________解釈学・コミュニケーション理論 言語論的転回 = 言語構築主義: 言語により世界は構築 - テクストの外には何もない(デリダ) ポストモダン言語構築主義相対主義 ⇒ ポストモダン以後自然主義的転回 (ジョン・サール)「言語」の哲学から「心」の哲学への転換 - 認知科学、情報科学、脳科学、生命科学と関連 メディア・技術論的転回 (ダニエル・ブニュー)
言語論的転回 → 語用論的転回 → メディオロジー的転回
思考から独立した存在を考える Ex. 人間消滅後の世界をどう理解するか |
|
1. 科学の哲学 philosophy of science (= s.l.): 科学の本質への哲学的考察 1662 英国王立学会(Royal Society)設立 → 会員は外国人含む。会誌発行 1666 フランス科学アカデミー 1700 ベルリン科学アカデミー 1724 ロシア科学アカデミー 1928 エルンスト・マッハ協会(初代会長Schlick M. 1882-1936, 独)
ウィーン学団が作った団体 協会員の多くがナチスのユダヤ迫害逃れ、米国等国外逃亡 Neurath O. 1882-1945, オーストリア 統一科学提唱 – 全科学は統一言語(物理)で記述できる 2. 科学的哲学 scientific philosophy (s.s.)科学の立場で基礎づけられた形而上学ではない哲学 = ウィーン学団Vienna Circle: 論理分析や言語分析を用いた科学哲学 Feyerabend, Paul Karl (1924.1.13-1994.2.11, オーストリア生)
通約不可能性(共役不可能性) incommensurability: 異なる理論体系(パラダイム)間に共通の理論的基盤がない時に、理論体系同士の比較を行うことが出来ないという状況のこと 現代経験主義2つのドグマ two dogmas of empiricism1950 クワイン「経験主義の2つのドグマ」
→ 知識・信念: 周辺が経験と接する全体連続的系をなす概念枠組。系を乱さない性向に従いつつ、経験に照らし未来予測する道具として、より感覚的刺激に適合するよう修正する実用主義こそ支持される 意味公準 meaning postulate 「意味公準」: そこに含まれる言葉の意味を決める命題 (カルナップ)
経験主義の2つのドグマ = 分析命題と綜合命題の区別不可能 → 反論 サピア-ウォーフ仮説 Sapir-Whorf hypotheses ウォーフ「言語、思想、現実性」1956 人間に「現実世界」は、集団言語習慣上に無意識構築 = 言語相対主義仮説 → 異言語は、異世界観を強制(単に、語彙だけではなく、文法構造も強く影響) |
Ex. フォピ・インディアン: 言語に時制を欠く → 時間観念がない
↔ 言語と観念の関係は相互的で動的であり、完全な決定関係ではない 観察なしでの知識 knowledge without observationアンスコーム「インテンション」1957.8.28 それを告げ知らせるものがなく、何の観察もなしだが、語りえ、それを知っている種類の知識 Ex. 自分の手足の位置は、感じずとも分かる。身体運動のみならず、心的原因mental causeも含まれる 行為から生じるものは観察からの知識 ⇔ 自分の行為は観察なしの知識 → 「○○しよう」とする: 行為と生じるものは区別されない
静的観想的知識: 事実先行し言葉がそれに一致するよう限定 理論負荷性 thepry-ladeness: ハンソン「発見のパターン」1958 感覚と解釈は切り離せず、事実認識は理論の投影があって成立 「見える」と「として見る」の区別、感覚し、解釈する、という二重認識説退ける xの観察は、xについて予め持つ知識に形成され、xという対象が見えることは、対象が我々の知るxと同じくふるまうだろうことを見ること。事実も、観察だけで得るのではなく、理論負荷的であり負荷的理論ともなる 無所有理論 no-ownership theory: ストローソン(『個体』1959.3) 問題 1) なぜ意識状況が身体の帰属する主体に帰属され、2) なぜ何かの主体に帰属されねばならないか デカルト派: 1)を、その主体は異なるタイプの実体とし解決 → 後者の問いを逃れえない ビトゲンシュタインら: 「無所有理論」 → 2)も解決 = 所有権が論理的に移譲可能なものだけが所有しうる
諸体験はある特定身体の状態に因果的に依存するという意味でない限り、何ものにも所有されない M述語: 物体にも適用されうるもの Ex. 「60 kgの重さである」「客間である」 P述語: 人物にしか適用されえないもの Ex. 「痛たがる」「笑っている」 人物概念は、両種の述語が適用可能である実体のタイプとし理解される。P述語を帰するのは、他者の運動を行為とし意図により解釈すること、つまり、我々が観察で他者に帰属させるものを、観察なしで自分に帰属させる自己帰属者として他者を見ることによる。P述語が集団にも帰属されるように、個体概念は、P述語の帰属する身体に依存するのではなく、P述語を帰属させられることそのものによる |