(2024年4月8日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 栄養段階
|
宮沢賢治「よだかの星」 ああ、かぶとむしや、たくさんの羽虫が、毎晩僕に殺される。そしてそのただ一つの僕がこんどは鷹に殺される。それがこんなにつらいのだ。ああ、つらい、つらい。僕はもう虫を食べないで飢えて死のう。いやその前にもう鷹が僕を殺すだろう。いや、その前に、僕は遠くの遠くの空の向うに行ってしまおう。 |
物質循環 + エネルギー流 → 食物連鎖(food chains, 食物網 food webs)
(一次)生産者(P, (primary) producer)生態系栄養動態論trophic dynamicsから見た無機栄養生物(独立栄養生物, autotroph)(生物群)。栄養段階の最基底をなす。無機物から有機物合成。緑色植物(特殊環境下の光合成細菌・化学合成細菌含む) 消費者(C, consumer)従属栄養生物中、取り入れた有機物の大部分をエネルギー順位の低い有機物に分解することを主に行う生物(群)。動物と他養植物(菌類・細菌類含めない)が属するが、普通は動物だけを指す。分解者との境界は曖昧で便宜的なもの。広く従属栄養生物全体を指す(s.l.)
第1次消費者(C1, primary consumer): 生産者(=緑色植物)あるいは生産者死体(落葉・枯死体等含む)を食べる。一般に草食動物(Ex. 昆虫) |
分解者(還元者) (D, docomposer or R, reducer)有機栄養生物で遺体・排出物あるいはその分解物を分解し、その際生じるエネルギーで生活。有機化合物を生産者が利用出来る無機化合物に戻す役割を果たす生物(群)。普通、他養性バクテリア・菌類を指すが、消費者との境は曖昧で、厳密にはバクテリアも動物も消費者及び分解者の両方の役割を果たすので、広く有機栄養生物全体を分解者と呼ぶ場合は消費者と同義となる転換者(Transformer)生態系の栄養動態(trophic dynamics)を特にエネルギー流(energy flow)を中心に見た場合における緑色植物以外の生物あるいは生物群の呼称。消費者・分解者の他に化学合成生物を含む |
|
生物群集の食う・食われるの結びつき (Elton 1927) P → C1 → C2 → C3 → C4 → C5 ↑__↘ ↓____↓____↓____↓____↓ D ← ← ← ← ← ← ← ← ← ← ______________食物連鎖 food chain 太陽光線を用いたエネルギー循環とみなす 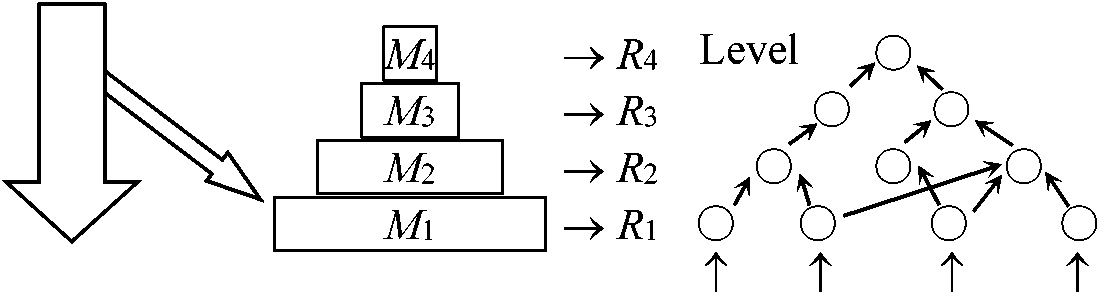
エネルギーピラミッド Energy pyramid 仮定: 定常状態i番目の栄養段階trophic levelでのエネルギーの出入り Pi – 1 = Pi + Ri: i番目に入るエネルギー量 ∴ Pi–1 – Pi = Ri > 0 (熱力学の第2法則) Pi–1 > Pi Pi–1/Mi: エネルギー代謝効率
単位iレベルで、その量を維持するためのエネルギー ∴ Mi > Mi+1 動物でのエネルギー代謝機構が共通(植物では逆転することもある) 食物網でのエネルギー循環動態定式化は可能である(解けるかどうかは別問題)
dxi/dt = Fi(x1, x2, … , x5), i = 1, 2, …, 5 P ⇒ B (black box) ⇒ R 競争、捕食-被捕食等の結合を取り入れた上で上式は作られているすると定常状態は
Fi(x1*, x2*, … , x5*) = 0
ここで ηが大きい(= Πが小さい)ほど効率がよい ここでいかなる相互作用interactionのときにηが大きくなるのか = 食物網の構造を調べる Margalef's hypothesis"successionはΠが小さい方に進む"多様性(diversity ≈ complexity)が大きいほど安定性stability大 Pr. (by May R)
dxi/dt = Fi(x1, x2, … , x5), i = 1, 2, … , 5, xi = 第i種の個体群密度
1. 定常点(x1*, x2*, … , x5*)を探す |
xi = xi* + ξi (i = 1, 2, … , 5) = Fi(x1*, x2*, … , x5*) + Σj=1sxj(∂Fi/∂xj) (Taylor展開)
∴ dξi/dt = Σi=1sAijxj … (1) (Aij = (∂Fi/∂xj)x = x* 対角線上(i = i)は種内関係。それ以外はi種に対するj種の影響
if Aij > 0 → (1)においてξjが増えるとdxi/dtが増え、ξjが減るとdxi/dtが減る
iとjの関係はcompetitior: Aij < 0, Aji < 0
系の安定性・不安定性は、この群集マトリックス値の組合わせでわかる 群集マトリックスAijの値をランダムにおいてλ1, λ2, … , λsの実数解をもとに確率的に安定性を調べ、sが大きいと殆どの場合が不安定と指摘 1972 May
s: 種数
σ√(sc) > 1: almost always unstable
⇒ σ√(sc)は多様性尺度の1つと見なせる
定性的安定性原理: a-d全てを満たすときに安定 dの意味はloopを作ることがないことを指す
______________ +
Exsistence of positive equiliblium: これまではxi*に正の解があると仮定していたがこれを撤廃する
dxi/dt = (bi + Σjaijxj)xi (i = 1, 2, … , s)
xi* = 0は絶滅モデルを指すので無意味 今後、現実系の特性を反映させたモデルを作る必要 (1985 寺元) |
|
森林 (forest)暖帯林 temperate forest 亜高山帯 subalpine zone 
|
湖沼 (池・小川) 珪藻(P) → ミジンコ (C1) → 小形魚 (C2) → 大形魚 (C3) → ゴイサギ (C4) 草原イネ科植物 (P) → バッタ (C1) → クモ (C2) → カエル → ヘビ → タカアユの食物連鎖 food chain of sweetfish
┌──→[ アユ ]─────┐
[ 藻類 ]───────────│→[ オイカワ・カワムツ ]
↑ └─→[ 水生昆虫 ]───↓─↓→[ カマツカ ]
[ 栄養塩類 ]←─────────[ 微生物 ]←─┘
水生生物群集 (海浜タイドプール)
| |
食物連鎖の長さトポグラフィー網の一般則(Pimm 1982, Cohen et al. 1986) 食物連鎖長は平均3程度で、5を越える事は殆どない ↔ 7以上の報告例 食物連鎖長の上限規定機構
他要因
生殖場所の異質性habitat heterogeneity → 連鎖長くなる |
ボトムアップ・トップダウン制御 bottom-up/top-down control捕食者↓ 捕食が植食者制御 top-down control ↓ └ 栄養カスケード(Power 1990): 捕食者除去実験 植食者 ↓ 餌資源制約が植食者制御 bottom-up control ↓ └ 緑世界仮説 green world hypothesis (Hairson et al. 1960) (否定的) 植物 栄養カスケード trophic cascade淡水生態系の例
↓ - [最上位捕食者 (シャチ)] + ↓ 肉食性魚類除去* |
|
三ピラミッドの総称 1) 個対数ピラミッド (数のピラミッド) Eltonian pyramid 普通小型動物が大型動物に捕食される + 小型動物は大型動物より速やかに増殖 → 食物連鎖段階(栄養段階)が進むにつれ相対的に個対数減少 食物サイズ = 口器に限定される → food chainは4-5 steps程度。同様に大きさ下限存在optimum problem 一定地域の生物を食物連鎖段階毎にとりあげ個体数を調べると一般にピラミッド状になるが時には逆転する
Ex. 1 一本の大きな木にそれを食べる蛾の幼虫が多数生育 現存量を栄養段階ごとに並べるとピラミッド状になる 現存量 standing crop: ある時点で単位面積上に存在する生物体総量biomass 3) 生産量(エネルギー)ピラミッド各栄養段階出入単位時間当たりエネルギー量(生産速度) 一般に栄養段階が1段上がる毎にエネルギー量は1/10-1/100減り完全なピラミッド状となる。また、植物生産量中、三次消費者生産にまで回るのは1/1000程度であり、多くの生態系で栄養段階数が3-5で収まるのはこのためである(Lindemann 1942) |
Ex. 湖のプランクトン(プ)は、植物性プより動物性プが現存量で上回る場合があるが、エネルギー量で示すとピラミッドの逆転はない。植物性プは短時間に成長し捕食を含めた死滅を繰り返すからである。諏訪湖の植物性プの年間平均現存量は0.07 t/ha(d.w.)だが、年間59世代繰り返し1年間に生産されるプランクトン総量は4 t/haに達する。ある段階の生物体が次の生物体として再生産される時、必ずエネルギーが呼吸等で失われエネルギーピラミッドは倒立しない 各栄養段階のエネルギー効率は栄養段階が上がるごとに一般には高まる。栄養段階の高い動物ほど一般に感覚や運動能力においてすぐれており、利用しうるエネルギーを効率よく利用できると考えられるLindeman (1942)
|