(Upload on July 7 2016) [ 日本語 | English ]
Mount Usu / Sarobetsu post-mined peatland
From left: Crater basin in 1986 and 2006. Cottongrass / Daylily
HOME > Lecture catalog / Research summary > Glossary > Mathematics > Calculus
|
Real number, ℜ Fig. ℜ can be thought of as points on a ruler Partial fraction decomposition (部分分数分解)Eq. (dx + e)/((fx + p)(gx + q)) = a/(fx + p) + b/(gx + q)d = 0, e = 1 ⇒ Eq. 1/((fx + p)(gx + q) = a/(fx + p) + b/(gx + q) Q. (2x2 + x - 4)/(x(x + 1)(x + 2))A. := a/x + b/(x + 1) + c/(x + 2) 2x2 + x - 4 = a(x + 1)(x + 2) + bx(x + 2) + cx(x + 1) = (a + b + c)x2 + (3a + 2b + c)x + 2a
∴ a + b + c = 2, 3a + 2b + c = 1, 2a = -4 → (a, b, c) = (-2, 3, 1) A. := (ax + b)/(2x2 -4x + 3) + (cx + d)/(x2 + 4x + 7)
5x3 - 12x2 + 6x + 17 = (ax + b)(x2 + 4x + 7) + (cx + d)(2x2 -4x + 3) = (-x + 2)/(2x2 - 4x + 3) + (3x + 1)/(x2 + 4x + 7) Q. 1/(x(x + 1)2)A. := a/x + b/(x + 1) + c/(x + 1)2
1 = a(x + 1)2 + bx(x + 1) + cx = (a + b)x2 + (2a + b + c)x + a |x| ≥ 0, |-x| = |x|, |x|2 = x2, |xy| = |x||y|, -|x| ≤ x ≤ |x| |
___|x| > A ⇔ x < -A, A < x (1) |x - 2| ≤ 3 (-3 ≤ x - 2 ≤ 3) ⇔ -1 ≤ x ≤ 5 (2) |2x + 1| ≥ 1 (2x + 1 ≤ -1, 1 ≥ 2x + 1) ⇔ x ≤ -1, 0 ≤ x (3) |x - 4| < 3x
(a). x - 4 ≥ 0 ⇔ x ≥ 4 & [x - 4 < 3x → x → x > -2] ⇒ x ≥ 4 (a) x < 7 ⇒ (x - 7 < 0 & x - 8 < 0) ⇒ -(x - 7) -(x - 8) < 3 6 < x < 7 (b) 7 ≤ x < 8 ⇒ (x - 7 ≥ 0 & x - 8 < 0) ⇒ +(x - 7) -(x - 8) < 3 (⇒ 1 < 3 ⇒ all ℜ) 7 ≤ x < 8 (c) 8 ≤ x ⇒ (x - 7 ≥ 0 & x - 8 ≥ 0) ⇒ +(x - 7) +(x - 8) < 3 8 ≤ x < 9 ⇔ 6 < x < 9 Th. triangle inequality (三角不等式), |a + b| ≤ |a| + |b|Pr. –|a| ≤ a ≤ |a|, –|b| ≤ b ≤ |b| ∴ –(|a| + |b|) ≤ a + b ≤ |a| + |b| → |a + b| ≤ |a| + |b| // = Q.E.D. (L) Th. a := a – b, |(a – b) + b| ≤ |a – b| + |b| ⇒ |a| – |b| ≤ |a – b|Ax. arithmetic-geometric mean (相加相乗平均) ∀a > 0, ∀b > 0 ⇒ (a + b)/2 ≥ √(ab), having equality (=) when a = b Pr. (left side)2 - (right side)2 = ((a + b)/2)2 - (√(ab))2
= (a2 + 2ab + b2)/4 - ab = (a2 - 2ab - b2)/4 = (a - b)2/4 ≥ 0 |
Sum formula (和の公式)n ∈ N (自然数), r ≠ 1 ⇒Σk=1n1 = n Σk=1nk = (n(n + 1))/2 Σk=1nk2 = (n(n + 1)·(2n + 1))/6 Σk=1nk3 = {(n(n + 1))/2}2 Σk=1nkk-1 = (rn - 1)/(r -1) ⇒ binomial theorem Ex. Σk=1n(k + 1)2 = Σk=1n(k2 + 2k + 1) = Σk=1nk2 + 2Σk=1nk + Σk=1n1 = (n(n + 1)·(2n + 1))/6 + 2·(n(n + 1))/2 + n = n·(2n2 + 9n + 13)/6 Def. combination (組み合わせ): nCr = (n!)/(r!(n - r)!)Def. factorial (階乗): n! ≡ 1 × 2 × … × n (0! = 1) |
Def. Binomial coefficient (二項係数): nCk = n!/(k!(n - k)!) Ax. n ≥ 2, k ≥ 1 ⇒ (1) knCk = nn-1Ck-1, (2) n-1Ck + n-1Ck-1 = nCk Pr._(1) knCk = k·n!/(k!(n - k)!) = (n·(n - 1)!)/((k - 1)!(n - k)!)
= n·(n - 1)!/((k - 1)!{n - 1) - (k - 1)}!) = nn-1Ck-1 // (2) nC0 - nC1 + nC2 - … + (-1)nnCn = 0 Def. double factorial (二重階乗): !! (symbol)
0!! = 1!! = 1, (n + 2)!! = n!!(n + 2) Pr. (Proof)
(2n)!! = 2 × 4 × … × 2n = (2 × 1) × (2 × 2) × … × (2 × n) = 2n × n! = 1 × 2 × 3 × 4 × … × 2n = (2n)! // |
|
Def. sequence (数列): a list of numbers or objects in a special order
{an} = {a1, a2, a3, … an} first term = a1__ith term = ai Ex. Sn+1 = 2Sn → Sn ≡ general term (一般項) Def. subsequence (部分列), {anp}np ∈ N, {ap} strictly increasing sequence ⇒ {anp} Ex. {an} = {a1, a2, a3, a4, …}, the following are the subsequences{a2n} = {a2, a4, a6, a8, …}, {an2} = {a1, a4, a9, a16, …} Def. finite difference (差分)Δf(x) = f(x + 1) – f(x), Δ0f(x):= f(x), Δ2f(x): = Δ (Δf(x)), … Δ(delta): forward difference operator (前進差分演算子) ∇f(x) = f(x) – f(x – 1), ∇0f(x):= f(x), ∇2f(x): = ∇(∇f(x)), … ∇ (nabla): backward difference operator (後進差分演算子) Def. arithmetic sequence (等差数列): an := a1 + (n - 1)d or am + (n - m)Def. common difference (公差) ≡ an+1 - an = d (constant) Ex. {2, 4, 6, …, 100} ∝ direct propotion (正比例) ↔ ∝-1 inverse proportion (反比例) Def. geometric sequence (等比数列): an := arn-1
Def. a ≡ first term (初項) Fibonacci sequence or series (フィボナッチ数列/級数)1202 Fibonacci, Leonardo (1170?-1250?): Liber Abaci (算盤の書)a1 = 0, a2 = 1, … ak = ak-1 + ak-2 (k > 1)
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, … 1843 Binet, Jacques Philippe Marie Eq. Binet's formula (ビネの公式)
= general term of Fibonacci sequence Circular constant, π (円周率)Eq. Leibniz formula (ライプニッツの公式)4/π = 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + … Eq. Euler's equation (オイラーの公式)π2/6 = 1 + 1/22 + 1/32 + 1/42 + 1/52 + 1/62 + … ζ function (ゼータ関数), ζ(s)= 1 + 1/2s + 1/3s + 1/4s + 1/5s + 1/6s + …s = 2 ⇒ Euler's equation Dirichlet L-function (ディクレルのL関数), L(s)= 1 - 1/3s + 1/5s - 1/7s + 1/9s - 1/11s + …s = 1 ⇒ Leibniz formula ε-δ definition (ε-δ論法)Th. For any ε > there exists a number m such that n > m implies |xn - a| < ε ≡ For all ε > 0 there exists some number m such that n > m → |xn - a| < ε≡ ∀ε > 0, ∃m: n > m → |xn - a| < ε Ex. limx→1|3x + 2| = 5 Pr. ∀ε > 0, ∃δ > 0 0 < |x – 1| < δ → |3x + 2 – 5| < ε → |3x – 3| < ε → |x – 1| < ε/3 [Take 0 < ε ≤ ε/3] ∵ ∀ε > 0, ∃δ < 1/3 → |3x – 3| < ε → |3x + 2 – 5| < ε // Ex. Prove limn→∞|(n + 1)/(n – 1)| = 1(Solve to be |(n + 1)/(n – 1)| < n0 to ∀ε > 0) Pr. (n + 1)/(n – 1) < 1 + ε depend, 2/(n – 1) < ε
→ 2/ε < n – 1, 2/ε + 1 = (2 + ε)/ε + 1 < n Pr. (proof by contradiction) if a ≠ b, ε0 := |a - b|/2 > 0 From the assumption of proposition, |a - b| < ε0 = |a - b|/2 ⇒ |a - b| < 0 contradiction // Def. limit value (極限値) Th. limn→∞|an+1/an| < 1 ⇒ limn→∞an = 0 Ex. an = Dn/n! (D = constant) → limn→∞(Dn/n!) = 0 Pr. _1. 0 < D ≤ 1 → trivial 2. an+1/an = {Dn+1(n + 1)!}/(Dn/n!) = D/(n + 1), limn→∞|D/(n + 1)| = 0 // Ex. Prove limn→∞(1/n2) = 0Pr. ∀ε > 0, N ∋ N(ε) := [1/√(ε)] + 1 ⇒ N(ε) > 1/√(ε)
On n ≥ N(ε), |1/n2 - 0| = 1/n2 ≤ 1/N(ε)2 < ε ∴ |1/n2 - 0| < ε Pr. ∀ε > 0, |(3n + 5)/(n + 1)| := 2/(n + 1) < ε
hold when n > 2/ε - 1
limn→∞an = a ⇒ limn→∞|an| = |a| Basic formula of limits (pl. formulae) (Fr.)Ax. convergence sequence (収束数列){an}, {bn}, ∀n ∈ N, an ≤ bn for all n, limn→∞an = a, limn→∞bn = b Th. Magnitude relationship of sequenceslimn→∞an ≤ limn→∞bn Pr. (proof by contradiction)
If limn→∞an = a, limn→∞bn = b, a > b. ε := (a - b)/2 n ≥ N1 ⇒ |an - a| < (a - b)/2 |
limn→∞bn = b ⇒ N2 = N2((a - b)/2) exist n ≥ N2 ⇒ |bn - b| < (a - b)/2
When n ≥ N2, |bn - b| < (a - b)/2 ⇒ bn - b < (a - b)/2 ⇒ bn < (a - b)/2 limn→∞(an ± bn) = a ± b Pr._ (∃N1 ∈ N)(∀n ∈N: n ≥ N1) |an - a| < ε/2, and
(∃N2 ∈ N)(∀n ∈N: n ≥ N2) |bn - b| < ε/2 ≤ |an - a| + |bn - b| < ε/2 + ε/2 = ε // Th. Limit of the product of sequences (数列の積の極限)limn→∞an·bn = ab Pr._ ∀ε, assuming 0 < ε < 1 + |a| + |b|, ε* = ε/(1 + |a| + |b|)
⇒ 0 < ε* < 1 n ≥ N1(ε*) ⇒ |an - a| < ε*, n ≥ N2(ε*) ⇒ |bn - b| < ε* N(ε) := max(N1(ε*), N2(ε*)) anbn - ab = b(an - a) + a(bn - b) + (an - a)(bn - b)
From triangle inequality and 0 < ε* < 1, if n ≥ N(ε), |b|ε* + |a|ε* + ε*2 = (|a| + |b| + ε*)ε* < (|a| + |b| + 1)ε* = ε // Th. Limit of the quotient of the sequence (数列の商の極限), b ≠ 0limn→∞(an/bn) = a/b Eq. limn→∞can = c·limn→∞an = caPr._c = 0 trivial
c ≠ 0, ∀ε > 0, limn→∞an = a ⇒ N1(ε/|c|) exists when ε/|c| > 0 |can - ca| = |c(an - a)| = |c||an - a| < |c|·(ε/|c|) = ε // Q. limn→∞((n2 + 2n + 3)/(3n2 + 2n + 1))A.__= limn→∞((1 + 2·1/n + 3·1/n2)/(3 + 2·1/n + 1/n2)) = limn→∞((1 + 2·0 + 3·0)/(3 + 2·0 + 0)) = 1/3 Th. squeeze, pinching or sandwich theorem (挟み撃ちの定理)
an ≤ cn ≤ bn (n ∈ N), limn→∞an = limn→∞bn = a
n ≥ N1(ε) ⇒ |an - a| < ε ∴ a - an < ε n ≥ N(ε) ⇒ an > a - ε, bn < a + ε
If n ≥ N(ε) ⇒ a - ε < an ≤ cn ≤ bn < a + ε Ax. [I] continuity of real numbers (実数の連続性)Ex. X = (1, 2] ⇒ maxX = 2, supX = 2, minX = not exist, infX = 1X: bounded Ex. X = [1, ∞) ⇒ maxX, supX = not exist. minX = infX = 1bounded below and unbounded above Th. [II] Weiestraß theoremAx. axiom of Archimedes (アルキメデスの公理)
∀a > 0, ∀b > 0, n ∈ N ⇒ ∃na > b Pr._ (i) ∀x ∈ C → x ≤ 0 (ii) ∀x > 0, ∃n ∈ N, nε > 1 (a := ε, b := 1, axiom of Archimedes) → ε > 1/n → -(1/n) > 0 - ε ∴ x > 0 - ε (∃x ∈ C) // Th. [III]Accumulate point or cluster point (集積点)interval (区間)open interval (開区間) (open set 開集合){x| a < x < b} ⇒ (a, b): --○-----○→
a, b: end point (終点). a, lower limit (下端). b, upper limit (上端) semi-open interval (半開区間) (semi-closed set 半開集合){x| a ≤ x < b}, {x| a < x ≤ b} ⇒ [a, b), (a, b]--●-----○→__--○-----●→ closed interval (閉区間), I (closed set 閉集合){x| a ≤ x ≤ b}: --●-----●→ ⇒ [a, b] (number line 数直線)
{x|x ≥ a} = [a, ∞) Def. positive and negative infinity (正負の無限大) {an}, ∃g > 0 for ∀n ≥ n0 (∈ N) ⇒ ∀an > g (< -g), {an} diverges at ±∞ or has limit at ±∞ ⇒ limn→∞an = ±∞ ∞ + ∞ = +∞, -∞ –∞ = -∞ ∞ + a = a + ∞ = +∞ a – ∞ = -∞, ∞ – a = +∞ ∞·∞ = +∞, ∞·(-∞) = -∞, (-∞)·(-∞) = +∞ a/∞ = a/(-∞) = 0 a > 0 → ∞·a = a·∞ = +∞, -∞·a = a·(-∞) = -∞, ∞/a = ∞, -∞/a = -∞ a < 0 → ∞·a = a·∞ = -∞, -∞·a = a·(-∞) = +∞, ∞/a = -∞, -∞/a = ∞ Prop. limn→∞(n√n) = 1 Pr. hn = n√n - 1, hn > 0 when n ≥ 2 (二項定理 →)
n = (n√n)n = (1 + hn)n = Σk=0nnCkhnk ≥ nC2hn2 = (n(n - 1))/2·hn2 Th. [IV] Cantor's intersection theorem (共通部分定理)Th. [V] Weierstraß-Bolzano (W-B) theorem(ワイヤシュトラウス-ボルザノの定理) |
|
Def. identiy (恒等式): an equation that is true whatever values are chosen, sometimes expressed by ≡
Ex. formula (公式), e.g., sin2θ + cos2θ = (or ≡) 1 Def. equation (方程式, s.l.): an amount is equal to another, expressed by =
Ex. 5x + 9 = 24 Quadratic equation (2次方程式): ax2 + bx + c = 0 p2/9 = 1 Cubic equation (3次方程式): ax3 + bx2 + cx + d = 0 x3 = 27 Rational equation (有理方程式): an equation that contains fractions with a variable in the numerator, denominator or both Ex. x/2 = (x + c)/4 Def. function (関数式): a relationship between variables, x and yx = independent variable ⇔ y = dependent variable Th. exsistence theorem (存在定理)Ex. Solve xn – 1 = 0
n = 1 ⇒ (x - 1) = (x - 1)(x + 1)(x2 + x + 1)(x2 - x + 1)
…
b2{(a/b)2 - 1} = b(a/b - 1)·b(a/b + 1) |
Def. cyclotomic equation (円分方程式) (Gauss 1801)
xn – 1 = 0_≡_(x – 1)(xn-1 + xn-2 + … + x + 1) = 0 Limit (of function) (関数の極限)Eq. p, q ∈ ℜ, p ≠ 0 ⇒ limx→a(px + q) = pa + qPr. ∀ε > 0, δ(ε) := ε/|p| > 0, 0 ≠ |∀x - a| < δ(ε) ⇒ |(px + q) - (pa + q)| = |p||x - a| < |p|δ(ε) = ε // Q. Prove f(x) = (x2 - 1)/(x - 1), x ≠ 1 ⇒ limx→1f(x) = 2A. f(x) = {(x + 1)(x - 1)}/(x - 1) = x + 1 ∴ limx→1f(x) = limx→1(x + 1) = 2 // Q. Prove limx→a√(x) = √(a), a > 0, x ≥ 0 A. ∀ε > 0, δ(ε) := √(a)·ε, 0 ≠ |∀x - a| < δ(ε) ⇒ |√(x) - √(a)| = |x - a|/(√(x) + √(a)) ≤ |x - a|/√(a) < δ(ε)/√(a) // Def. left/right-hand limit (左/右極限)Ex1. limx→1+0(1/(x - 1))
∀K > 0, δ1(K) := 1/K > 0, 1 < x < 1 + δ1(K) ⇒ 1/(x - 1) > 1/δ1(K) = K
∀K < 0, δ2(K) := -1/K > 0, 1 - δ2(K) < x < 1 ⇒ 1/(x - 1) < 1/δ2(K) = K
∀ε, δ(ε) > 0, 0 < x < δ(ε) ⇒ 0 < √x < √δ = ε ∴ limx→1+0√x = 0 |
|
Def. continuous (連続): limf(x) = f(a) ⇒ continuous at x = a Def. continuous: satisfying the following three conditions
1) limf(x) exist.__2) f(a) exist.__3) limf(x) = f(a) |f(x) - f(a)| < ε Th. f(x), g(x) continuous on I, λ, μ; ∈ ℜ ⇒λf(x) + μg(x), f(x)g(x), f(x)/g(x) (g(x) ≠ 0), |f(x)| continuous Ex. discontinuity on limit function of continuous function, f(x)fn(x) on I = [0, 1], fn(x) = xn (n = 1, 2, 3, …) fn(x) is continuous function at ∀n, f(x) := limn→∞fn(x) Case. 0 ≤ x < 1: fn(x) = xn is:geometric sequence of first term = x and, common ratio = x f(x) = limfn(x) = limxn = 0 Case. x = 1: fn(1) = 1 ∴ f(1) = limfn(1) = 1
f(x) = 0 (0 ≤ x < 1), f(x) = 1 (x = 1) therefore, f(x) is not continuous on I ≡ limit of continuous function is not always continuous ⇒ Unconditionally change the order of two limitslimx→1-0{limn→∞fn(x)} ≠ limn→∞{limx→1-0fn(x)} |
Ex. discontinuity on infinite sum of continuous function, f(x) fn(x) = x2/{(x2 + 1)n-1} (n = 1, 2, 3, …), fn(x) continuous on ∀n in ℜ
f(x) = Σn=1∞fn(x) = x2 + x2/(x2 + 1) + x2/(x2 + 1)2 + … ⇒ f(x) = x2/(1 - 1/(x2 + 1)) = x2 + 1 Case. x = 0: fn(0) = 0, f(0) = Σn=1∞fn(0) = 0f(x) = x2 + 1 (x ≠ 0), f(x) = 0 (x = 0) ∴ limx→0f(x) = limx→0(x2 + 1) = 1 ≠ f(0) ∴ f(x) is not continuous at x = 0 ∴ f(x) is not continuous function in ℜ ≡ infinite sum of continuous function is not always continuous ⇒ Unconditionally change the order of two limitslimx→0{limm→∞Σn=1mfn(x)} ≠ limm→∞{limx→0Σn=1mfn(x)} Th. intermediate-value theorem (中間値の定理)Q. Show an odd-degree equation, x2n+1 + a2nx2n + … a1x + a0 =0, has a real root. A. f(x) := x2n+1 + a2nx2n + … a1x + a0, f(x) continuous on ℜ
limx→∞f(x) = ∞__limx→-∞f(x) = -∞ ⇒ |
|
Ex. f'(x) = c' = 0 (c: constant): f'(x) = lim((c - c)/h) = limh→00 = 0 Ex. f'(x) = x' = 1: f'(x) = lim((x + h) - x)/h = lim(h/h) = lim1 = 1 Ex. f'(x) = (xn)' = nxn-1: f'(x) = lim(x + h)n - xn)/h
= lim((xn + nxn-1h + nC2xn-2h2 + … + hn) - xn)/h Interval ≡ I, f(x), g(x) diff., λ, μ ∈ ℜ (1) λf(x) + μg(x) diff. ⇒ {λf(x) + μg(x)}' = λf'(x) + μg'(x)__(微分の線形性) (2) f(x)g(x) diff. ⇒ {f(x)g(x)}' = f'(x)g(x) + f(x)g'(x) (3) f(x)/g(x) diff. (g(x) ≠ 0) ⇒ {f(x)/g(x)}' = {f'(x)g(x) + f(x)g'(x)}/g(x)2 if f(x) = 1 ⇒ (1/g(x)' = -g'(x)/g(x)2 Pr. (1) h ≠ 0, {(λf(x + h) + μg(x + h)) - (λf(x) + μg(x))}/h =λ·{f(x + h) - f(x)}/h} + μ·{g(x + h) - g(x)}/h} ⇒ λf'(x) + μg'(x) (h → 0) // Pr. (2) g(x) continuous, h ≠ 0, {f(x + h)g(x + h) - f(x)g(x)}/h =
{f(x + h)g(x + h) - f(x)g(x + h) + f(x)g(x + h) - f(x)g(x)}/h = ⇒ f'(x)g(x) + f(x)g'(x) (h → 0) // Pr. (3) g(x) continuous, h ≠ 0, {f(x + h)/g(x + h) - f(x)/g(x)}/h =
[{f(x + h)g(x) - f(x)g(x + h)}/{g(x + h)g(x)}]/h = Ex. y = (x2 + 5)(x3 - 2) ⇒ y' = (x2 + 5)'(x3 - 2) + (x2 + 5)(x3 - 2)' = 2x(x3 - 2) + (x2 + 5)·3x2 = 5x4 + 15x2 - 4x Ex. y = 2/(x2 + 1) ⇒ y' = 2·{-(x2 + 1)'/(x2 + 1)2} = -4x/(x2 + 1)2Th. Differentiation of composite function (合成関数の微分) Ex. y = (x2 + 1)10 ⇒ (z := x2 + 1), y' = dy/dz·dz/dx = 10(x2 + 1)9·(x2 + 1)' = 10(x2 + 1)9·2x = 20x(x2 + 1)9 Th. inverse function theorem (逆関数定理)(1) function of single variable: (f-1)'f(a) = 1/f'(a) (2) function of multiple variables: JF-1(F(p)) = [JF(p)]-1 Ex. y = x1/m → y' = 1/m·x1/m–1 ∵ y = x1/m → x1/m, the relationship of xm is inverse function → (x = y1/m) y = xm Pr. x = ym, dx/dy = nym–1∴ dy/dx = 1/nym–1 = 1/m·1/(x1/m)m–1 = 1/m·x1/m–1 Ex. y = xn/m → y' = n/m·xn/m–1Pr. y = (x1/m)n, t = x1/m → y = tn, dt/dx = 1/m·x1/m–1 ∴ dy/dx = dy/dt·dt/dx = ntn-1·(1/m)·x1/m–1 = n(x1/m)n–1·(1/m)·x1/m–1 = n/m·x(n–1)/m+1/m-1 = n/m·xn/m–1 Ex. a ≠ 1, a > 0, x = ay ⇔ y = logaxPr. (loga(x + h) – logax)/h = 1/h·(loga(x + h) – logax) = 1/h·loga(1 + h/x) = 1/x … loga(1 + h/x)x/h (∵ limx→±∞(1 + 1/x)x = e)
h → 0, y' → (1/x)·logae Pr. sin-1x/dx = 1/(dsiny/dy) = 1/cosy = 1/√(1 – x2) ∵ siny = x |
Ex. a ≠ 1, a > 0, y = ax ⇒ x = logay Pr. dy/dx = 1/(dx/dy) = 1/(dlogay/dy) = 1/(1/y·logae) = 1/[(1/y)·(loge1/logea)] = y·logea = ax·logea Ex. y = 3√x (x > 0) ⇒ x = y3, dx/dy = 3y2 = 3(3√x2)∴ y' = dy/dx = 1/(dx/dy) = 1/(3(3√x2) Logarithmic differentiation (対数微分法)Th. f(x), g(x) [a, b] diff. ⇒(f(x) ± g(x))' = f'(x) ± g'(x), (f(x)·g(x))' = f'(x)·g(x) + f(x)·g'(x) Pr._ F(x) = f(x) ± g(x), G(x) = f(x)·g(x)(F(x + h) – F(x))/h = {f(x + h) ± g(x + h) – (f(x) ± g(x))}/h
= (f(x + h) – f(x))/h ± (g(x + h) – g(x))/h (G(x + h) – G(x))/h = (f(x + h)·g(x + h) – f(x)·g(x))/h = (f(x + h) – f(x))/h·g(x) + f(x)·(g(x + h) – g(x))/h Elementary function ( 初等関数 )Differentiation of elementary functions (初等関数の微分)Th. Diff. of log and exponential functions (対数・指数関数の微分)Exponential function: (ax)' = axloga (a > 0)_____ ⇒ a = e: (ex)' = ex Logarithmic function: (loga|x|)' = 1/(xloga) (a > 0) ⇒ a = e: (log|x|)' = 1/x Pr1. y := ax, logy = logax = xloga ∴ 1/y·dy/dx = loga ∴ dy/dx = yloga = axloga // Pr2. (loga|x|)' = (log|x|/a)' = 1/(xloga) //Th. Differentiation of power function (冪関数の微分) Th. Differentiation of a few elementary functions (諸初等関数の微分) Differentiation of trigonometric functions (三角関数の微分)
(sinx)' = cosx
(sin-1x)' = 1/√(1 – x2)
x = siny (-1 < x < 1, -π/2 < y < π/2), x' = cosy > 0
1/2·log(x2 + y2)·(x2 + y2)'
(sinhx)' = coshx |
|
Ax. Equations of n-order derivatives (n次導関数公式)
(1) (ex)(n) = ex
(1) {f(ax + b)}(n) = anf(n)(ax + b)
⇒ {f(ax + b)}(n) = anf(n)(ax + b) // |
Law (generalized) Leibniz rule (ライプニッツの法則) f(x), g(x), n-order diff. ⇒ (f(x)·g(x))(n) = Σk=0nnCkf(n–k)(x)·g(k)(x)
n = 1: {f(x)g(x)}' = f'(x)g(x) + f(x)g'(x) A. (x)(k) = 0 (k ≥ 2) → y(n) = Σk=0nnCk(x)(k)(e2x)(n-k) = x(e2x)(n) + n(x)'(e2x)(n-1) = x·2ne2x + n·1·2n-1e2x = 2n-1(2x + n)e2x |
|
Th. Taylor's theorem (Taylorの定理) Th. Maclaurin's theorem (Maclaurinの定理) [a = 0 on Taylor's theorem] Q. Express ex as f(x) = Σk=0n-1(f(k)(0)/k!·xk) + f(n)(θx)/n!·xn (0 < θ < 1) Then, express the sum of 5th-order polynomial and residual term. |
A. f(n)(x) = ex (n = 0, 1, 2, …), f(n)(θx) = eθx
∴ ex = Σk=0n-1(1/k!·xk) + eθx/n!·xn |
|
Def. Landau's symbol (ランダウの記号), o Th. operation of Landau's symbol: x → 0
o(xn)o(xm) = o(xn+m) When x → 0, equations shown below hold:
ex = Σk=0n(xk/k!) + o(xn) Extreme value (極値)= local maximum (極大値) + local minimum (極小値)Q. Obtain the extreme of f(x) = x2/ex using 2nd derivative A. f'(x) = 2xe-x - x2e-x = x(2 - x)e-x
x = 0, 2 when f'(x) = 0 increase rates are different among them Q. Obtain lim(2n/n!)A. when n ≥ 4 ⇒ 0 < 2n/n! = 2/1·2/2·2/3·2/4 … 2/(n - 1)·2/n < 2/1·2/n = 4/n → 0 (n → 0)__∴ lim(2n/n!) = 0 // n! shows higher increase rate than 2n Th. 0 ≤ a < 1, {an}, lim|an+1/an| = a ⇒ liman = 0Pr. γ := (a + 1)/2, 0 ≤ a < γ < 1 (∵ a < 1) ε = γ - a > 0, N ∋ N = N(γ - a) exist n ≥ N ⇒ ||an+1/an| - a| < γ - a here, if n ≥ N |an+1/an| - a ≤ ||an+1/an| - a| ⇒ |an+1| < γ|an| repeat using this inequality when n > N 0 ≤ |an| < γ|an-1| < γ2|an-2| < … < γn-N|aN| from 0 < γ < 1, limγn-N|aN| = 0 // |
Q. Show lim(na/rn) = 0 A. bn := na/rn > 0
bn+1/bn = (n + 1)a/rn+1·rn/na = 1/r·(1 + 1/n)a ⇒ 1/r (n → ∞) rn shows higher increase rate than na Q. Prove Solve f(x) = sin-1(x/√(1 + x2)) - tan-1xA. y := x/√(1 + x2), f(x) = sin-1y - tan-1x → f'(x) = 1/√(1 - y2)·y' - 1/(1 + x2) Here √(1 - y2) = √(1 - x2/(1 + x2)) = 1/√(1 + x2),
y' = (√(1 + x2) - x·(2x/2√(1 + x2)))/(√(1 + x2) = 1/((1 + x2)(√(1 + x2)) 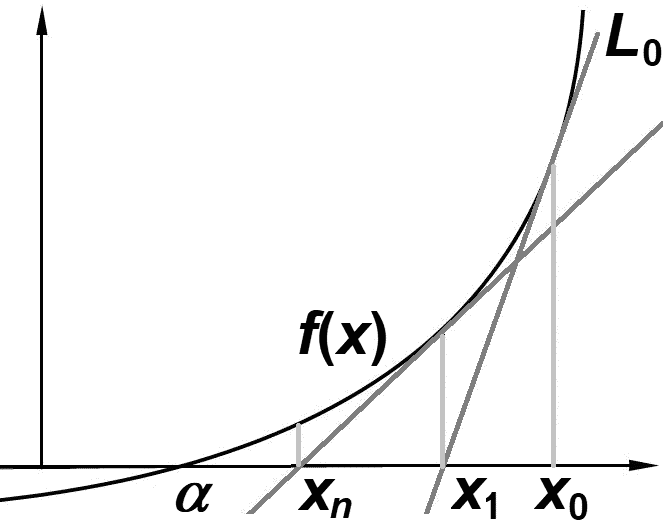 Ex. √a: f(x) = x2 - a → f'(x) = 2x, f''(x) = 2
Ex. √a: f(x) = x2 - a → f'(x) = 2x, f''(x) = 2
xn+1 = xn - (xn2 - a)/2xn = (xn2 + a)/2xn
n = 1: (1 + 5)/2 = 3 Limit of indeterminate forms (不定形の極限値)Th. l'Hôpital's rule (ロピタルの定理)Ex. lim{(-3x2 + 7x + 4)/(2x + 5)} = lim{(-3x + 7 + 4/x)/(2 + 5/x)} = -∞ Ex. lim(x3 - 4x2 -5x -6) = lim{(-3x + 7 + 4/x)/(2 + 5/x)} = -∞ Ex. lim(logx/√x) = lim((1/x)/(1/2√x)) = lim(2/√x) = 0 Ex. limxlogx = limlogx/(1/x) = lim(1/x)/(-1/x2) = lim(-x) = 0 These are not indeterminate forms Def. indeterminate form (不定形): an expression involving two functions whose limit cannot be determined solely from the limits of the individual functions
seven indeterminate forms which are typically considered |
|
Def. (Riemann) integration: a = ∫abf(x)dx ⇒
∫aaf(x)dx = 0, ∫baf(x)dx = -∫abf(x)dx Ex. f(x) = c (c: constant) ⇒ I = [a, b] integrable, ∫abcdx = c(b - a)Ex. f(x) = x ⇒ I = [a, b] integrable, ∫abxdx = 1/2·(b2 - a2) Ex. f(x) = x2, 0 ≤ a < b ⇒ I = [a, b] integrable, ∫abx2dx = 1/3·(b3 - a3) Def. lower sum and upper sum (不足和・過剰和) I = [a, b], f(x) bounded, Δ = {xk}, Ik := [xk-1, xk] mk = inff(x), Mk = supf(x) (k = 1, 2, … n) ⇒
lower sum ≡ sΔ(f) = Σk=1nmk(xk - xk-1)
Σk=1nmk(xk - xk-1) ≤
Σk=1nf(ξk)(xk - xk-1) ≤ Σk=1nMk(xk - xk-1) |
a partition Δ' made by a new cutoff point c
only one k, which supports xk-1 < c < xk, exists Note that SΔ'(f) ≤ SΔ(f) consider the lower sum: 0 ≤ sΔ'(f) - sΔ(f) ≤ (Mk - mk)(xk - xk-1)Note that sΔ(f) ≤ sΔ'(f) In general, sΔ(f) ≤ sΔ'(f) ≤ SΔ'(f) ≤ SΔ(f) (Δ ⊂ Δ')Δ = {xk}, Δ' = {yl} → Δ'' := {xk} ∪ {yl} ⇒ sΔ(f) ≤ sΔ''(f) ≤ SΔ''(f) ≤ SΔ'(f) ∴ sΔ(f) ≤ SΔ'(f) sΔ(f) bounded above on Δ and SΔ'(f) bounded below on Δ Def. upper integral and lower integral (上積分・下積分)I = [a, b], f(x) bounded ⇒
upper integral ≡ -∫abf(x)dx = infSΔ(f) on the greatest lower bound of Δ Th. amplitude (振幅), ω(f, I) Ex. I = [1, 3], f(x) = x2 ⇒ supf(x) = 9, inff(x) = 1 ∴ ω(f, I) = 9 - 1 |
|
Def. primitive function (原始関数) ≡ F(x) ∃G'(x) = f(x), F(x), G(x) diff., F'(x) = G'(x)
⇒ F(x) – G(x) = C (C: constant of integration 積分定数) Pr. [a, b] ∋ ∀a → f(x) = f(a) + (x – a)f'(c) = f(a) = C // 2) f(x), g(x), [a, b] diff., f'(x) ≡ g'(x) → f(x) = g(x) + k Pr. F(x) := f(x) – g(x) reduce (1)
F(x) = F(a) + (x – a)F'(c) = {f(a) – g(a)} + (x – a)(f'(c) – g'(c)) Integration by substitution (置換積分)Ex. Ex. I = ∫(x/√(1 + x2))dx: t := 1 + x2, dt/dx = 2x∴ xdx = 1/2dt → I = ∫√t·1/2dt = 1/2·2/3t3/2 = (1/3)·√(1 + x2)3 Ex. I = ∫(ax + b)/√(x2 + 2px + q)dx (p ≠ q)
[I = ∫(ax + b)/√{(x + p)2 + q – p2}dx] = ∫at/√(t2 + q – p2)dt(1) + ∫(b – ap)/√(t2 + p – q2)dt(2) (1) I1: t2 + q – p2 = u, 2tdt = du ∴ I1 = a/(2√u)du = a√u = a√(t2 + q + p2)
(2) = I2 = (b – ap)log(t + √(t2 + q – p2)) = a√(x2 + 2px + q) + (b – ap)log(x + p + √(x2 + 2px + q)) Th. integration by parts (部分積分)∫f(x)g(x)dx = f(x)G(x) - ∫f'(x)G(x)dxEx. ∫xexdx = xex - ∫1·xexdx = xex - ex + C |
(C, omit – often done) Basic formulae (基本公式)Ax. 1) ∫(f'(x)/f(x))dx = log|f(x)|Pr. (log|f(x)|)' = f'(x)/f(x) // Ax. 2) ∫f(x)αf'(x)dx = f(x)α+1/(α + 1) (α ≠ -1) 0) ∫{af(x) + bg(x)}dx = a∫f(x)dx + b∫g(x)dx 1) ∫xαdx = xα+1/(α + 1) 2) ∫(1/x)dx = log|x| 3) ∫1/(a2 + x2)dx = 1/a·tan-1(x/a) 4) ∫1/(a2 – x2)dx = (1/2a)·log{(a + x)/(a – x)} (|x| < a) 5) ∫1/(x2 – a2)dx = (1/2a)·log{(x – a)(x + a)} (|x| > a) 6) ∫1/√(a2 – x2)dx = sin-1(x/a) (|x| < a) 7) ∫1/√(x2 – a2)dx = log(x + √(x2 – a2)) (|x| > a > 0) 8) ∫1/√(x2 + a2)dx = log(x + √(x2 + a2)) 9) ∫√(a2 – x2)dx = 1/2·{x√(a2 – x2) + a2sin-1(x/a)} (|x| < a) 10) ∫√(x2 – a2)dx = 1/2·(x√(x2 – a2)) + a2log(x + √(x2 + a2))) (|x| > a > 0) 11) ∫√(x2 + a2)dx = 1/2·(x√(x2 + a2)) + a2log(x + √(x2 + a2)) 12) ∫eaxdx = 1/a·eax 13) ∫axdx = 1/loga·ax 14) ∫sinaxdx = -1/a·cosax 15) ∫cosaxdx = 1/a·sinax 16) ∫1/sin2axdx = -1/a·cotax 17) ∫1/cos2axdx = 1/a·tanax 18) ∫tanaxdx = -1/a·log(cosax) 19) ∫cotaxdx = 1/a·log(sinax) Integration of rational functions (有理関数の積分)Ax. f(u, v) rational functions on u and v, t := tan(x/2) ⇒∫f(cosx, sinx)dx ⇒ expressed by the integral of rational function on t Q. Solve ∫1/(2 + cosx)dxA. 1/(2 + cosx)dx = 1/(2 + (1 - t2)/(1 + t2)·2/(1 + t2)·dt = 2/(3 + t2)dt ∴ ∫1/(2 + cosx)dx = ∫2/(3 + t2)dt = 2/√3·tan-1(t/√3) = 2/√3·tan-1(1/√3·tan(x/2)) Q. Solve ∫(cosx/(2 + sin2x))dxA. t := sinx → dt = cosxdx ∫(cosx/(2 + sin2x))dx = ∫(1/(t2 + 2)dt = 1/√2·tan-1(t/√2) = 1/√2·tan-1(sinx/√2) Integration of irrational function (無理関数の積分)Ex. ∫(1/(√x + √(x + 1))dx = ∫(√(x + 1) - √x)dx = 2/3·(x + 1)3/2 - 3/2·x3/2 |
Basic equations of definite integralsTh. f(x) continuous on I, F(x) := primitive function of f(x), α, β ∈ I⇒ ∫αβf(x)dx = F(β) - F(α) ≡ [F(x)]αβ Pr. F(x) = ∫axf(t)dt + C∴ F(β) - F(α) = (∫aβf(t)dt + C) - (∫aαf(t)dt + C) = ∫aβf(t)dt + ∫αaf(t)dt = ∫αβf(t)dt // Th. f(x) diff. on I, f'(x) integrable on I, α and β ∈ I ⇒ ∫αβf'(x)dx = f(β) - f(α)Th. f(x) continuous on I, a(x) and b(x) diff. on J, a(x) and b(x) ∈ I (x ∈ J) ⇒ d/dx∫a(x)b(x)f(t)dt = f(b(x))b'(x) - f(a(x))a'(x) Pr. F(x) := the primitive function of f(x) → ∫a(x)b(x)f(t)dt = F(b(x)) - F(a(x))
differentiate both sides = f(b(x))b'(x) - f(a(x))a'(x) // Ex. d/dx∫ax2f(t)dt = f(x2)·(x2)' - f(a)·a' = 2xf(x2)Solution of definite integral1) Quadrature by parts (区分求積法)Ex. ∫0πsinxdx → π/n := h A.__SΔ = Σhsinnh, 2sin(h/2)·SΔ = Σhsin(nh)·2sin(h/2) = h{Σ2sin(nh)·sin(h/2)} = -h[(cos3h/2 – cosh/2) + (cos5h/2 – cos3h/2)
+ (cos7h/2 – cos5h/2) + ∴ 2sin(h/2)·SΔ = -h{cos(2n + 1)h/2 – cos(h/2)}, SΔ = -h{cos(2n + 1)h/2 – cos(h/2)}/{2sin(h/2)}
n → ∞, h = π/n → 0 |
Th. Characteristics of definite integrals 1) linearity (線形性) 2) ∫abf(x)dx = ∫acf(x)dx + ∫cbf(x)dx no matter how the relationships between a, b and c are large or small Pr. c is a dividing point on Δ = {xk} →
Δ1 and Δ2 are divisions of [a, c] and [c, b], respectively = (Σk=1l + Σk=l+1n)supf(x)(xk - xk-1) = S[a,c]Δ1(f) + S[c,b]Δ2(f) Here, |Δ1| ≤ |Δ|, |Δ2| ≤ |Δ|, select c as cutoff point, |Δ| < 0 ⇒ |Δ1| < 0, |Δ2| < 0 -∫abf(x)dx = -∫acf(x)dx + -∫cbf(x)dx ⇒ true on upper integral As well, true on lower integral f(x) integrable on [a, b] ⇒ -∫abf(x)dx = -∫abf(x)dx ⇒ -∫acf(x)dx + -∫cbf(x)dx = -∫acf(x)dx + -∫cbf(x)dx when -∫acf(x)dx = -∫acf(x)dx, -∫cbf(x)dx = -∫cbf(x)dx, the equation holds ∴ f(x) integrable on [a, c] // 3) monotonicity (単調性)4) absolute value inequalities (絶対値の不等式) |
|
Ex. ∫01(1/√x)dx ⇒ t > 0 → lim(1/√x) = ∞ ∴ ∫t1(1/√x)dx = [2√x]t1 = 2 - 2√t Here, lim(2 - √t) = 2 (convergence) ∴ ∫01(1/√x)dx = 2 Ex. ∫01(1/x)dx ⇒ t > 0 → ∫t1(1/x)dx = [log|x|]t1 = -logtlim(-logt) = ∞ (divergence) Ex. ∫01logxdx → limlogx = -∞, t > 0∫t1logxdx = [xlogx - x]t1 = -1 - tlogt + t. From l'Hôpital's rule, limtlogt = lim∫t1logt/(1/t) = lim((1/t)/(-1/t2)) = lim(-t) = 0 ∫01logxdx = lim∫t1logxdx = lim(-1 - tlogt + t) = -1 |
Ex. ∫-11(1/x)dx → lim(1/x) = ∞, lim(1/x) = -∞
∴ ∫-11(1/x)dx = ∫-10(1/x)dx + ∫01(1/x)dxdivergence → divergence Integral test (収束判定法)Comparison test (比較判定法) Th'. Absolute converge of improper integral (広義積分の絶対収束)
f(x) integrable on [a, ∞], ∫a∞|f(x)|dx convergence ⇒ Def. f(x) indefinite integrable on I, I = (a, b], [a, b), [a, ∞) or (-∞ b] (1) ∫I|f(x)|dx converge ⇒ ∫If(x)dx converge ≡ absolute converge (絶対収束) (2) ∫I|f(x)|dx diverge, ∫If(x)dx converge ⇒ ∫If(x)dx ≡ conditional converge (条件収束) Γ-function and β-function (ガンマ関数・ベータ関数) |
Area (面積), SDef. y = f(x) ≥ 0, [a, b] ⇒ S = ∫abydx = ∫abf(x)dx≡ the area enclosed by y = f(x) and lines, x = a and x = b Th. f(x), g(x) continuous, f(x) > g(x) (a ≤ x ≤ b) ⇒ S = ∫ab{f(x) - g(x)}dx≡ the area enclosed by y = f(x), y = g(x) and lines, x = a and x = b Q. Obtain the area enclosed by f(x) = x/(x2 + 4) and g(x) = x/8A. f(x), g(x) odd fucctions, S = double of area in x ≥ 0
x/(x2 + 4) - x/8 = (x(4 - x2)/(8(x2 + 4)) ≥ 0 ⇔ 0 ≤ x ≤ 2 r = sinθ and θ = 0 (0 ≤ θ ≤ π/2) A. S = 1/2∫0π/2(1 + cosθ)2dθ - 1/2∫0π/2sin2θdθ = 1/2∫0π/2
= 1/2∫0π/2(1 + 2cosθ + cos2θ - sin2θ)dθ Length (長さ), lTh. Arc length of a curve (弧長), L:C → x = φ(t), y = ψ(t) (α ≤ t ≤ β), φ(t), ψ(t) C1-class ⇒ L = ∫αβ√{(dx/dt)2 + (dy/dt)2}dt = ∫αβ√{φ'(t)2 + ψ'(t)2}dt |
Corollary. Arc length (弧長), L: y = f(x) C1-class (a ≤ x ≤ b) ⇒
L = ∫ab√(1 + f'(x)2)dx Pr. x = t, y = f(x) ⇒ L = ∫ab√((dx/dt)2 + (dy/dt)2)dt = ∫ab√(1 + f'(x)2)dx //Q. Obtain the arc length (L) of y = coshx (0 ≤ x ≤ log2) A. y' = sinhx, coshx ≥ 0 → √(1 + y2) = √(1 + sinh2x) = √cos2x = coshx ∴ L = ∫0log2coshxdx = [sinhx]0log2 = sinh(log2) = (2 - 1/2)/2 = 3/4 Co. Arc length on polar coords, L: C, r = f(θ) C1-class (α ≤ θ ≤ β) ⇒L = ∫αβ√(f(θ)2 + f'(θ)2)dθ Pr. r = f(θ) on xy coordinate → x = rcosθ = f(θ)cosθ, y = rsinθ = f(θ)sinθ(dx/dθ)2 + (dy/dθ)2 = (f'(θ)cosθ - (f(θ)sinθ)2 + (f'(θ)sinθ - (f(θ)cosθ)2 = f'(θ)2(cos2θ + sin2θ) + f(θ)2(cos2θ + sin2θ) = f'(θ)2 + f(θ)2 ∴ L = ∫αβ√((dx/dθ)2 + (dy/dθ)2)dθ = ∫αβ√(f(θ)2 + f'(θ)2)dθ // Volume and lateral (surface) area (体積・側面積), V and SlQ. Obtain V and Sl of sphere of which radius is aA. the sphere ≡ solid revolution of which semicircle is y = √(a2 + x2) V = π∫-aay2dx = π∫-aa(a2 - x2)dx = π/6·{a - (-a)}3 = 4/3·πa3 y' = -x/√(a2 - x2) → √(1 + y'2) = √(1 + x2/(a2 - x2)) = a/y ∴ Sl = 2π∫-aay√(1 + y'2)dx = 2π∫-aaadx = 4πa2 |
[ sequence ]
|
Def. series (級数): S = Σan = Σn=1∞an = a1 + a2 + … + an + …
Def. nth item (第n項) = an Def. geometric series (等比級数/幾何級数), In:
the sum of geometric sequence between the first term to nth term when the first term = 1 and common ratio = p Cf. Mersenne number (メルセンヌ数) Def. converge (収束) Σn=1∞ak = s ⇔ divergence (発散)Ex._Σn=1∞xn, |x| > 1 → convergent to 1/(1 – x)
|x| ≤ 1 → divergence |
Prop. infinite geometric series, a ≠ 0
|r| < 1 ⇒ Σn=1∞arn-1 = a/(1 - r) convergence Σn=1∞(aan ± bbn) = aΣn=1∞an ± bΣn=1∞bn Pr. Sn, Tn nth partial sum ⇒ Σn=1∞(aan ± bbn) = aSn + bTn∴ aS + bT (n → ∞) // Th'. Σn=1∞an = s ⇒ Σn=1n1an + Σn=n1+1∞an = sQ. obtain the sum of series Σn=1∞{1/(n(n + 1))} A. conduct partial fraction decomposition: 1/(n(n + 1)) = 1/n - 1/(n + 1) nth partial sum, Sn = Σk=1n{1/k - 1/(k + 1)}
= (1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + … + (1/n - 1/(n + 1)) ∴ Σn=1∞{1/(n(n + 1))} = limSn = lim(1 - 1/(n + 1)) = 1 Sequence of functions (関数列)Th. Weierstrass M-test (ワイエルシュトラウスのM判定法)Ex. Σn=1∞(sinnx/n2): |sinnx/n2| ≤ 1/n2 for ∀n ∈ N, ∀x ∈ ℜ
Σn=1∞(1/n2) convergence (Weierstrass M-test) |
|
Convergence radius or radius of convergence (収束半径) ≡ r A power series with radius of convergence r Ex. Obtain r of Σn=0∞((n + 1)/n!·xn) an := (n + 1)/n! → lim|an/an+1| = lim[(n + 1)/n!·{(n + 1)!/(n + 2)}] lim{(n + 1)2/(n + 2)} = ∞ ∴ r = ∞ Th. Abel's continuity theorem (Abelの連続性定理)f(x) = Σn=0∞an convergence ⇒ limΣn=0∞anxn = Σn=0∞an Pr. f(x) = Σn=0∞anxn (|x| < 1), sn = a0 + a1 + … + an, Σn=0∞an := s → Σn=0manxn = Σn=0m(sn – sn–1)xn = Σn=0msn(xn – xn+1) + smxm = (1 – x)Σn=0msnxn + smxm (s–1 := 0)
|x| < 1, m → ∞ → f(x) = (1 – x)Σn=0∞snxn, 1 = (1 – x)Σsnxn |
Abel transform (Abelの変換) Σn=0manxn = Σn=0m(sn – sn–1)xn
= Σn=0msn(xn – xn+1)xn + smxm Th. Term-by-term integration theorem (項別積分定理)Th. Term-by-term differentiation theorem (項別微分定理) Q. Obtain the value of ∫01Σn=0∞{(n + 1)/3n·xndx A. an = (n + 1)/3n → r of Σn=0∞anxn = lim|an/an+1| = lim{(n + 1)/3n}
= lim{3(n + 1)/(n + 2} = 3, uniform convergence on [0, 1] = Σn=0∞[xn+1/3n]01 = Σn=0∞(1/3n) = 1/(1 - 1/3) = 3/2 |
|
Trigonometric series (三角級数), f(x)
= a0/2 + a1cosx + b1sinx + … + ancosnx + bnsinnx + … → can be assumed as f(x) (–π ≤ x ≤ π) continuous → Fourier seriesan = 1/π∫-∞∞f(x)cosnxdx (n = 0, 1, 2, …), bn = 1/π∫-∞∞f(x)sinnxdx (n = 1, 2, …)
Def. an, bn Fourier coefficient (フーリエ係数) sn(x) = a0/2 + Σk=1n(akcoskx + bksinkx) = ∫-ππf(t)dt + Σk=1n(coskx·1/π∫-ππf(t)cosktdt + sinkx·1/π∫-ππf(t)sinktdt)
= 1/π∫-ππf(t){1/2 + Σk=1ncos(t – x)}dt
= 1/2[sin(t/2) + Σk=1n{sin(k + 1/2)t – sin(k – 1/2)t}] ∴ Sn(x) = 1/π∫-ππf(t)[{sin(n + 1/2)(t – x)}/2sin{(t - x)/2}]dt 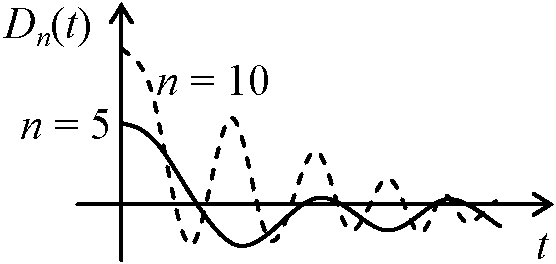 Dirichlet kernel (ディリクレ核), Dn(t) := {sin(n + 1/2)t}/2sin(t/2) → even function (偶関数) 1/π∫-ππDn(t)dt = 1 (f(t) ≡ 1) |
Dirichlet integral (ディリクレ積分), sn(x) = 1/π∫-ππf(t)Dn(t – x)dt
= 1/π∫-ππf(t + x)Dn(t)dt Th. Riemann-Lebesgue: f(x) period = 2π continuous function, n → ∞→ Fourier coefficient = 0 (convergence), i.e., an → 0, bn → 0 Pr. (prove an → 0), πan = ∫-ππf(x)cosnxdx, x := t – π/nπan = ∫-π+π/nπ+π/nf(t – π/n)cosn(t – π/n)dt = ∫-ππf(t – π/n)cosntdt = –∫-ππf(x – π/n)cosnxdx 2πan = –2∫-ππf(x)cosnxdx – ∫-ππf(x – π/n)cosnxdx = ∫-ππ{f(x) – f(x – π/n)}cosnxdx
f(x) [-π, π] uniformly cont., 0 < ε, 0 < N < ∀n, |f(x) – f(x – π/n)| < ε ⇒ Σn=1∞an2, Σn=1∞bn2 converge together Pr. αn, βn
J =Def ∫-ππ(f(x) – {α0 + Σn=1k(αncosnx + βnsinnx)})2dx + πΣn=1k{(an – αn)2 + (bn – βn)2}
→ αn = an (n = 1, 2, …, k), βn = bn (n = 1, 2, …, k) in minimum, J ≥ 0 |
|
Th. limf(x, y) = α, limg(x, y) = β, λ, μ ∈ ℜ ⇒
(1) lim{λf(x, y) + μg(x, y)} = λα + μβ |
Th. (x, y) nbd of (a, b), (x, y) ≠ (a, b), f(x, y) ≤ g(a, b)
limf(x, y) = α, limg(x, y) = β ⇒ α ≤ β Th. (squeeze theorem) (x, y) nbd of (a, b), (x, y) ≠ (a, b),|f(x, y) - α| ≤ g(x, y), limg(x, y) = 0 ⇒ limf(x, y) = α Ex. lim(xy/√(x2 + y2)) = 0
r := √(x2 + y2), |x| ≤ r, |y| ≤ r, (x, y) ≠ (0, 0) → |
|
Def. Partial derivative (偏導関数)
fx(x, y) ≡ lim[{f(x + h, y) - f(x, y)}/h] Ex. u = f(x, y, z) = sin(xyz) → ux = yzcos(xyz), uy = xzcos(xyz), uz = xycos(xyz) Def. totally differential (全微分可能), df(x, y)Ex. f(x, y) = xy (x > 0) → fx(x, y) = yxy-1, fy(x, y) = xylogx ∴ df(x, y) = yxy-1dx + xylogxdy High-order partial derivative (高次偏導関数)Ex. obtain all 2nd-order partial derivative of z = f(x, y) = x3 + 3x2y + y2
z = f(x, y) C2-class → zx = 3x2 + 6xy, zy = 3x2 + 2y Partial differentiation of composite function (合成関数の偏微分)Th. f(t) diff. on I, g(x, y) ∈ I partial diff. on D, (x, y) ∈ D ⇒
F(x, y) = f(g(x, y)) partial diff. on D, φ'(x) = gz(x, y) → ∂/∂x·F(x, y) = f'(g(x, y))gx(x, y). yas well // Th. f(x, y) totally diff. on D, φ(t), ψ(t) diff. on I, (φ(t), ψ(t)) ∈ D (t ∈ I) ⇒F'(t) = fx(φ(t), ψ(t))φ'(t) + fy(φ(t), ψ(t))ψ'(t) z = f(x, y), x = φ(t), y = ψ(t) ⇒ dz/dt = ∂z/∂x·dx/dt + ∂z/∂y·dy/dt |
Th. f(x, y) totally diff. on D, φ(s, t), ψ(s, t) partial diff. on E,
(φ(s, t), ψ(s, t)) ∈ D ((s, t) ∈ E) ⇒
Fs(s, t) = fx(φ(s, t), ψ(s, t))φs(s, t) + fy(φ(s, t), ψ(s, t))ψs(s, t) ∂z/∂s = ∂z/∂x·∂x/∂s + ∂z/∂y/∂y/∂s, ∂z/∂t = ∂z/∂x·∂x/∂t + ∂z/∂y/∂y/∂t Q. When f(x, y) C1-class on R2, x = u2 + v2, and y = uv, proveg(u, v) = f(u2 + v2, uv) ⇒ vgu(u, v) + ugv(u, v) = 4yfx(x, y) + xfy(x, y) A. gu(u, v) = ∂/∂u·f(u2 + v2, uv)= fx(u2 + v2, uv)·∂x/∂u + fy(u2 + v2, uv)·∂y/∂u = 2ufx(x, y) + vfy(x, y) __gv(u, v) = ∂/∂v·f(u2 + v2, uv)
= fx(u2 + v2, uv)·∂x/∂v + fy(u2 + v2, uv)·∂y/∂v = 2vfx(x, y) + ufy(x, y)
= v{2ufx(x, y) + vfy(x, y)} + u{2vfx(x, y) + ufy(x, y)} Application of partial derivative (偏導関数の応用)Def. f(x, y) C2-class ⇒C2-class → fxy = fyx ∴ Hesse matrix ⊂ symmetric matrix Def. Hessian, H(x, y) ≡ determinant of Hessian matrixDef. f(x, y) = 0, y = g(x), f(x, g(x)) = 0 ⇒ y = g(x) ≡ implicit function (陰関数) Def'. f(x, y, z) = 0, z = g(x, y), f(x, y, g(x, y)) = 0 ⇒z = g(x) ≡ implicit function (陰関数) Q. Obtain y' and y'' of y = ex+yA. diff. by x, y is the function of x → y' = ex+y(1 + y') ∴ (1 - ex+y)y'
If 1 - ex+y ≠ 0, then y' = ex+y/(1 - ex+y) |
Repeated or iterated integral (累次積分)Q. Obtain the value of I = ∫01{∫x1ey2dy}dxA. I = ∫01{∫y1ey2dx}dy = ∫01yey2dy = [1/2·ey2]01 = (e - 1)/2 |
ClassificationOrdinary differential equation, ODE (常微分方程式)Partial differential equation, PDE (偏微分方程式) Algebraic differential equation, ADE (代数微分方程式) |
Ax. Laplace transform on elementary function (1) L[eat](s) = 1/(s - a) (s > a)______(4) L[sinωt](s) = ω/(s2 + ω2) (s > 0) (2) L[tn](s) = n!/sn+1 (s > 0)_______ (5) L[coshωt](s) = s/(s2 - ω2) (s > |ω|) (3) L[cosωt](s) = s/(s2 + ω2) (s > 0) (6) L[sinhωt](s) = ω/(s2 - ω2) (s > |ω|) Q. Solve y'' - 3y' + 2y = 4e3t, y(0) = 0, y'(0) = 1 A. L[y(t)] := Y(s) →
L[y] = Y
∴ (s2Y - 1) - 3sY + 2Y = 4/(s - 3) after Laplace transform |
|
Q. Obtain the solution of: y'' - 2xy' - 2y = 0, y(0) = 1, y'(0) = 0 A. (apply term-by-term differentiation) → y = ex2 |