(2017年1月16日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 数学
|
量、構造、変化、空間様式研究 → 公理的に定義される抽象的構造について形式論理を共通枠組みとし探究 純粋数学: 数学の伝統的流れに抽象概念を導入(抽象的学問) 17C デカルト、フェルマー → 解析幾何学 ニュートン、ライプニッツ - 微積分 calculus 代数学 algebra: 整数論・代数幾何学 幾何学 geometry: 微分幾何学・位相幾何学(トポロジー) topology 解析学 calculus : 微分方程式・確率論・数理統計学 応用数学 applied mathematics: 近代産業諸技術の裏付けとなる理論や他学問との境界領域 近代: 数理統計・記述統計・推測統計 数学を必要とする学問 (基本的には全分野)
ルネサンス以降 数学記号 mathematical symbols+ (正符号, プラス)/- (負符号, マイナス)1489 Widmann Jhon (+ → ラテン語 et の速記) xの加法 addition に関する逆元を表すために負符号を用い-xと記す → バランスでx自身を+xと書くこともある → 1521 Schreiber Heinrich: 加法(+)と減法(-)の意味に拡張 x + y (和), x – y (差) だたし、x - yは通常x + (-y)と定義される √ (根号, ルート): n√xはxのn乗根を表す (rootのrが記号の元)1525 Rudolff Christoff 「代数学」 (nが2のときに単に√xと書くことが多い) = (等号, イコール, equality sign) Recorde Robert 1510-1558 "The whetstone of witte", 1577 (平行線が元) Def. 等式: 等号を含む式 ⇔ ≠ (不一致, ノットイコール)≈ (ほぼ等しい, nearly equal, circa): どの位の違いを認めるかは文脈による ÷ (除法, 割る) "/"も用いられる 1659 Rahn Johann Heinrich → 「x ÷ y」はxをyで割った商を表す . (小数記号) Stevin Simon 1548-1620: ただし、記号は現在のものと異なる <, > (不等号 = 大小関係/順序, 小なり/大なり, inequality sign) 「x < y」はxとyの間に何らかの順序が定まり、xの方が「先」であることを示す Def. 不等式: 不等号を含む式 |
Bouguer Pierre → 「x ≤ y」は「x < yまたはx = y」のこと ≪, ≫ (大小関係, 非常に小/大): どれ位小さい(大きい)かは文脈による × (乗法 multiplication, 掛ける) Oughtred William 1574-1660 (現在は*, ·, ×いずれかを用いる) Σ (シグマ, 加法/無限和), Σi=1nai = a1 + a2 + … + an → Σi=1∞ai Π (パイ, 乗法/無限積), Πi=1nai = a1 × a2 × … × an → Πi=1∞ai Ex. n! = Πi=1ni 数学的帰納法 mathematical induction自然数に関する命題証明の演繹的手法(名前は帰納法だが)Th. 01 (最小元の存在): ∀a ∈ A ⊂ N, A ≠ ∅ ⇒ ∃a0 ≤ a Th. 02 (数学的帰納法の原理): n ∈ N, P(n) (P = proposition 命題) (1) 1 ⊂ A, (2) if n ⊂ A ⇒ n + 1 ⊂ A ⇒ A = N Pr._A ≠ A' ⊂ N, if A' ≠ ∅ ⇒ Th. 01より∃n0 ∈ A'
(1)からn0 > 1 ∴ n0 - 1 ≥ 1, n0 ∉ A (1) n = 1の時に成立 ≡ P(1)は真 (2) n = kの時に命題成立と仮定 ⇒ n = k + 1の時にも成立 ⇒ P(n)は全ての自然数nについて成立 Pr._P(n)が真となる自然数n全体の集合をAとする ⇒ Th. 02 (1), (2)を満たす ∴ A = N ⇒ P(n)は全てのNで成立 // Q. ∀n ∈ N ⇒ n! ≥ 2n-1A.__(1) n = 1 ⇒ LS = 1! = 1, RS = 20 = 1 成立 (2) n = kの時に k! ≥ 2k-1成立と仮定 (k +1)! - 2k = (k +1)·k! -2·2k-1 ≥ (k +1)·2k-1 -2·2k-1 = (k -1)·2k-1 ≥ 0 (∵ k > 1) ∴ (k + 1)! ≥ 2k → n = k + 1の時も成立 // |
|
集合(標本空間) set, S: ≡ 範囲を定義できる集まり(= 要素が明確)
Ex. 北海道大学学生 (≡: 定義記号) Def. 全体集合(普遍集合), U: 定義された集合の要素全体の集合ラッセルのパラドクス: 自分自身を要素としない(X ∉ X)集合Xを全て集めたもの(:= V)は集合ではない Pr. If Vは集合 → V ∈ V or V ∉ V (集合でなければこの仮定は意味なし)
1. V ∈ V → Vは自分自身を要素とする集合 → Vの定義よりV ∉ V 外延的表現: 全構成成分を書く Ex. {1, 2, 3} 内包的表現: Sの元で命題P(x)が真となる全てを集めた集合(共通性質示す)
∈: 属するin ⇔ ∉: 属さない (∈の否定)_¬: 否定 Ex. ¬(x ∈ S) = x ∉ S
→ 集合S上の関係Rが以下の3つの性質(同値律)を満足する 1. 反射律: xRx 2. 対象律: xRy → yRx 3. 推移律: xRy, yRz → xRz (同値)類: Ca = {x|x ∈ S, aRx}Th. 1: R~S → Rによる類はSの部分集合として等しいか互いに素かのいずれかであり、Sは互いに素な類の和集合として表される Th. 2: 集合Sが互いに素な部分集合(≠ 空集合)の和集合として表されるとき、Sの要素a, bが同一の部分集合に属しているとして、それをaRb → R~S Pr. 1:_ Ca := {x|x ∈ S, aRx}, Cb := {y|y ∈ S, aRy} → (a) Ca∩Cb ≠ φ, (b) Ca∩Cb = φ (a) ∃x ∈ Ca∩Cb → ∀x ∈ Ca → aRx∩aRz ∴ xRa∩aRz ∴ xRz … (1)
同様にyRz … (2)
同じ類に属するという関係をRで表す
類別: 互いに素である類に分類すること ≡ 元を1つも含まない集合 → 全ての集合の部分集合 ∅⊂∅ Ex. {x ∈ ℜ: x2 + 1 = 0} = ∅ Def. 部分集合 subset: 集合A, B, 任意のBの要素がAにも属する ⇒ B ⊂ A
φ: 全ての集合の部分集合 集合系 system of sets≡ ある集合Sの元が全てそれ自身集合である集合S冪(べき)集合 power set≡ ある集合Aの部分集合を全部集めた集合, 記号P(A)集合X = ∅ → P(X) = {∅} [P(X) = ∅とはならない] 部分集合系, Si≡ ある1つの普遍集合Xの冪集合P(A)の任意の部分集合から成る集合系 |
Def. ベン図 Venn diagram (Venn J, 英, 論理学)
集合関係を全体集合を長方形で部分集合を円で表した図 A⊃B ⇔ ∀b ∉ B → b ∉ A Ex. X = {x| x2 + x - 2 ≤ 0}とY = {x| x2 - x - 12 < 0}の関係X = {x| - 2 ≤ x ≤ 1}, Y = {x| -3 < x < 4} ⇒ X ⊂ Y Th. 推移律: 集合A, B, C. A⊂B, B⊂C → A⊂C (Pr. trivial)Def. 2) A⊇B: AはBの部分集合 subset Def. 3) 相等 A = B → AとBは等しい certification: ∀a ∈ A → A⊂B, ∀b∈B → b ∈ A, A⊃B ∴ A = B ↔ A ≠ B
= [等しい、イコール] 集合の一致 ↔
 Law. 基本公式 (basic formulae) 表. 集合論と確率論の用語の対応: 集合論と確率論は密接に関係
記号 集合論 確率論 (備考)
Ω 全体集合 標本空間 (必ず起こる事象に対応)
∅ 空集合 空事象 (決して起こらない事象)
ω∈∅ Ωの要素 状態state of nature (根元事象)
A∈F Fの要素 事象 (状態の集まったもの)
Ac 補集合 余事象
∪Ai 合併集合 和事象 (∪i=1n or ∪i=1∞)
∩Ai 共通部分 積事象 (∩i =1n or ∩i=1∞)
A∩B=∅ 互いに素 AとBは排反事象
A⊂B 部分集合 Aが起こる時Bも起こる
|
[ 微分・積分 ]
|
Def. 写像: ƒ: A → B, ƒ(x) = y → yをƒによるxの像(値), xをƒによるyの原像
C⊆A, D⊆B, ƒ(C) = {ƒ(c)|c ∈ C}, ƒ-1(D) = {a ∈ A|ƒ(a) ∈ D} →
それぞれƒによるBの像, ƒによるDの原像 Def. 制限写像 f|c: f|c(c) = f(c) → fの作用をC (C ⊆ A)に制限することでCからBへの写像ができるAからBへの写像f, g, ∀a ∈ A, f(a) = g(a) → f = g, そうでなければf ≠ g Def. 単射 injection: f: A → B, a, b ∈ A →
f(a) = f(b)ならば常にa = bであれば単射 → Def. |A| ≤ |B| fはAからBへの1対1対応(写像) Def 2. 全単射 bijection: fが全射かつ単射 = 1対1対応(一意対応)y = f(x): A = [a, b] → Def. B [A ≡ fの定義域 domain, B ≡ fの値域(終域) range]Ex. f(x) = √xの定義域, I = [0, ∞] Ex. A = {1, 2, 3}, B = {a, b, c, d} ⇒
{f(1) = c, f(2) = a, f(3) = d},
{g(1) = b, g(2)= d, g(3) = b},
{h(a) = 2, h(b) = 1, h(e) = 2, h(d) = 3}
→ f, gはAからBへの写像, f ≠ g Pr. 0 < x ≤ 1 → 1 ≤ 1/x, 1/x ∈ B ∴ fはAからBへの写像
1) ∃y ∈ B → 1 ≤ y ∴ fは全射 Def. 濃度: 集合 X, Yが対等 → |X| = |Y| (XとYの濃度は等しい) Def. 有限集合 finite set, X ≠ ∅: ∃m 自然数, |X| = |{1, 2, … m}|
→ |X| = m (Xの濃度はm) Th. (Bernstein): X, Y, |X| ≤ |Y|, |Y| ≤ |X| → |X| = |Y| Th. 集合X → |X| < |P(X)| Pr. ƒ: X ∋ x → {x} ∈ ∃P(x) → |x| ≤ |P(X)| (|X| ≠ |P(X)|を示す)
If g: X → ∃P(X), V := {x ∈ X|x ∉ g(x)} ∈ P(X) |
Def. 冪集合の濃度: P(X) = 2Xの濃度 → 2|X| Def. 合成写像(= 積), f○g [読み まる、コンポジット] 写像fと写像gの合成 → f○g = f(g(x)) 合成順序を逆に定義する(g(f(x)))流儀もある
合成写像: f: A → B, g: B → C, a ∈ A, f(a) = b ∈ B, g(b) = c ∈ C ⇒ g(f(a)) = c → gfと表す Def. 順序対 ordered pair: 順序を考慮に入れた対Ex. a ≠ b → (a, b) ≠ (b, a) → 順序列(a, b) Def. 集合族: {Uλ|λ ∈ Λ}, 添字集合: ΛDef. 直積: A × B = {(a, b)| a ∈ A, b ∈ B}
Case P × P = P2 [A × B ≠ B × A] Def. 恒等写像 identity mapping, identity function, f: A → A → Aの変換 [xをx自身に写す写像] → 1A: A → A, 1A(x) = x と表す Def. 逆写像(s.s.): f(a1) ≠ f(a2) → f(a) = b, g(b) = a, g: B → A (≡ f-1)
f(a) = b → f-1(b) = a Euler: 定義域 = 関数が数学的意味を持つよう暗黙中に定められる ゼロ点 zero point 定義されない
⇒ 関数式 function expression or formula: 関数を表す式 Def. fのグラフ: {(a, f(a)| a ∈ A} ⊆ A × B
Def. 不動点(固定点, fixed point or fixpoint): f(x) → xとなるx 線形変換(一次変換) linear transformationam = an (m < n), an-m = e, at = t, t ∈ N ⇒Def. 位数 order: tのうち最小のもの(ある群の元の個数) → o(a) = tと表す 群の元xに対しordxはxの生成する巡回群の位数を表す ブラックボックス black box入力 input, x → [ ƒ (ブラックボックス) ] → 出力 output, y = ƒ(x)ブラックボックスモデル: 入力と出力の関係のみを扱う → 箱の中は無視 Def. 関数 function: yはxに対して決まっている
Ex. 1
Ex. 2
ブラックボックス上は、Ex. 1, Ex. 2は同じ関数となる 関数結合: ブラックボックスƒに入力し、その出力をブラックボックスgに入力し、その出力を最終出力→ 2個のブラックボックスを結合したものは、やはり1つのブラックボックス |
|
数 number: 数量を表すために用いる抽象的概念
⇔ 数字 ≡ 数を表す記号(混同されるが、本質的に異なる) Ex. リンゴ1個 ≠ ミカン1個 → 共通するものを見出し、それを1と名付ける1という数自体はリンゴやミカンではないし、それが存在するという事実を指す訳でもない。まして縦や横に引かれた短い線分を言うわけではない 四元数, H or ℍ複素数 complex number, C or ℂ (正確には複素数全体の集合。以下同) 実数 real number, R or ℜ 有理数 rational number, Q or ℚ: 整数の比で書ける数 整数 integer (number), Z or ℤ
正数(正の整数) (= 自然数 natural number), N or ℕ 分数 fractional number: 分母 denominator と分子 numerator を整数で表わすことができる数
有限小数 finite decimal
純循環節 pure recurring period: 循環節が小数第1位から始まる 無理数 irrational number: 循環しない無限小数 infinite decimal |
√2 = 1.41421356 一夜一夜に人見頃____√3 = 1.7320508 人並に奢れや 虚数 imaginary number, ℑ (i, i2 = -1) 小数 decimal (fraction): (s.s.)
s.l. 絶対値が1より小さく零でない実数を位取り記数法で表したもの Pr. f: N → M, f(n) = 2n (n ∈ N), ∃x ∈ M → x = 2n = f(n) ∴ fは全射
n, m ∈ N, n ≠ m → 2n ≠ 2m, f(n) ≠ f(m) ∴ fは単射 Def. 可算濃度(可付番濃度) ℵ0, アレフ・ゼロ: Nの濃度 → |N| = |Z| = |Q| = ℵ0 Def. 可算集合(可付番集合, 可算無限集合): Nと対等な集合 Ex. Z, QDef. 非可算集合: 可算でない無限集合 Def. 高々可算集合 (at most countable) = 有限集合 + 可算集合 Def. 連続体濃度 (cardinality of continuum) ℜ, アレフ: Rの濃度 Th. ℜ0 = |N| = |Z| = |Q| < |R| = |(a, b)| = ℜ H. 連続体仮説 (continuum Hypothesis, CH)ℵ0とℜの間には他の濃度が存在しない(証明不能が証明されている)H. 一般連続体仮説 (general CH, GCH) |
|
集合 M: 演算(符号sign) *を考える (四則演算 four arithmetical operations)
積 product, c = ab ⇔ 商 quotient, a = c/b (b ≠ 0) (除法 division)
Th. 単位元・逆元は1つしか存在しない → Def. 単位群: 単位元のみの部分群(eと表す) Pr. ∃ax = e, x'y' = e →ey = (ax')y' = a(x'y') = ae = a, ea = e(ey') = (ee)y' = ey = a → 逆元(乗法): ax = xa = eDef. x := a-1 ≡ 逆元 Def. 可換群(アーベル群): 交換法則(律) (commutative law) x*y = y*x成立する (xとyは交換可能) 演算集合Def. 加群: 可換群中、算法が加法(+)で表され交換法則が成り立つ演算集合 (単位元"0") 移項 transition: 一方にある項を、符号を変えもう一方の項に移すこと Ex. a + b = c → a + b – c = 0 Def. 有限群: 群 G = 有限集合→ Def. 位数: Gの要素の個数nのこと → |G| = n Def. 部分群: H ⊆ G, 部分群HがGと同じ演算に関し群をなす → HはGの部分群(G自身も部分群)Th. Hが群Gの部分群である条件: a, b ∈ H → ab-1 ∈ H Pr. a ∈ H → aa-1 = e ∈ H. ea-1 = a-1 ∈ H. a, b ∈ H → a(b-1)-1 ∈ H Th. 群Gの有限部分集合Hが部分群になるための条件: a, b ∈ H → ab ∈ H Pr. a, a2, a3, … ∈ H. as = at (s < t)なるs, t (integer)存在
If at-s = e → |
Ex. 整数 ⊂ 有理数 ⊂ 実数 ⊂ 複素数 → 順次部分群となる 表. 数の集合: 交換法則 a*b = b*a (○ = 群を作る, ×, 群を作らない)
加法
乗法
群G, 要素 n ⌊x⌋ フロアー (floor function): 実数x に対し⌊x⌋はxを超えない最大の整数 ⌈x⌉ セイル (ceil function): 実数xに対し⌈x⌉はxを下回らない最小の整数 Th. 因数定理: xの整式P(x), P(a) = 0 → P(x)は(x – a)で割切れる ⇔ P(x)が(x – a)で割切れるならP(a) = 0
Ex. f(x) = x3 - 6x2 + 11x –6, f(1) = f(2) = f(3) = 0 → [記号] 〈•〉 [山括弧] 生成する部分群(巡回群): 群G, S ⊆ G → 〈s〉はSの生成する部分群 Case. Sが一元集合S = {x} → 〈x〉とも書く(= xの生成する巡回群) Def. 自己(準)同型
Ker [カーネル] 核(零空間): 群や環の準同型、ベクトル空間間の線形写像 φ に対しKer φはその凖同型の核 Def. 環: 演算·(×)と+につき、それぞれモノイドと加群をなし、分配法則(律) x·(y + z) = x·y + x·zを満たす演算集合Def. 体: 可換環でかつ乗法についても逆元をもつ集合 Ex. 集合が、有理数全体(除0)、実数全体(除0)、n次正則行列全体 |
整数の除法 (entire division)Def. 自然数 N: 1から始まり1を足すという操作で作られる数の集合Th. A ⊆ N → ∃min(A) Th. A ⊆ N, 1 ∈ A, x ∈ A, x + 1 ∈ A → A = N (数学的帰納法の原理) Th. ε < ∀b → b < na, ∃n (加法と乗法の定義) Th. (除法の原理) ∃a ∈ Z, 0 < b ∈ Z →
a = qb + r, 0 ≤ r ≤ b, ∃1q ∈ Z, ∃1r ∈ Z
Def. q: aをbで割った商 Def. r: 余り Def(記号). mod, % [モジュロ]: a mod b → aをbで割った余り (a%b → コンピュータ分野記法, Rでは%%) Def. aはbの倍数 multiple ⇔ Def. bはaの約数 divisor Pr. 存在を証明 → 唯一性を証明 (帰納法) 自然数 (1) a = 1: b = 1 → a = b1 + 0, b > 1 → a = b0 + 1 ⇒ 定理を満たす (2) a = nで成立と仮定 ⇒ ∃n = bq + r (0 ≤ r < b)
i) 0 ≤ r < b - 1 → n + 1 = bq + (r + 1) 負数: a < 0 → -a > 0 ⇒ -a = b∃q + ∃r (0 ≤ r < b)
⇔ a = b(-q) + (-r) (-b < -r ≤ 0) a, b > 0で成立しないと仮定 ⇒
a = bq + r (0 ≤ r < b), a = bq' + r' (0 ≤ r' < b), q ≠ q' ∨ r ≠ r' b(q - q') + (r - r') = 0 ⇔ b(q - q') = r' - r
∴ b|r' - r A. 3m + 4n = 3(4q + 3) + 4(6q + 2) = 36q + 17 = 12(3q + 1) + 5 ∴ 5 Def. 公倍数: 2つ以上の整数に共通な倍数 (0は常に公倍数) Def. 最小公倍数(least common multiple, L.C.M.): 公倍数中最小の数 Def. 公約数: 2つ以上の整数に共通な約数(1は常に公約数) Def. 最大公約数(greatest common measure, G.C.M.): 公約数中最大の数 表記 gcm(a, b, …), 自明であればgcmは省略 Th. ユークリッドの互除法(最大公約数を求める方法)(1) a > b > 0 (a ∈ Z, b ∈ Z ⇒ (a, b) = (r, b) (2) {rn}, r1 = a, r2 = b, n ≥ 2
(a) rn > 0 → rn+1 = [rn-1をrnで割った余り] |
Pr. (1) (a, b) := d1 → a = a'd1, b = b'd1 → r = a'd1 - b'd1q = d1(a'b'q) → rはd1で割り切れる (+ d1はbとrの公約数) → d1 ≤ (b, r) = d2 (b, r) := d2 → b = b'd2, r = r'd2 → a = b'd2q + r'd2 = d2(b'q + r') →d2 ≤ (a, b) = d1 ∴ d1 = d2 ⇒ (a, b) = (b, r) ___(2) (除法の定理)
rk > 0 → r1 = a > r2 = b > r3 > … > rk > rk+1 ≥ rk+2 ≥ … ≥ 0 Q. (390, 273) A._ 390/273 = 273·1 + 117 → (390, 273) = (273, 117)
273/117 = 117·2 + 39 → (273, 117) = (117, 39)
一般式: a1x1 + a2x2 + … + anxn = k Def. 素数 prime number: 自然数で1とその数自身の他に約数持たない数(1 ∉ 素数) Def. 合成数 composite number ≡ 素数以外の自然数 Ex. 全ての偶数
偶数 even number ≡ 最小の素数2で割り切れる数 = 2の倍数 multiple Th. 「整数論の基本定理」各合成数は順序を除いて同じ素数分解に到達するTh. 素数の無限性: 素数は無限個存在 → 素数の平均分布 Pr. (背理法) – ピタゴラスにより証明される
if n [全素数の数] →set finite, p1, p2, p3, …, pn → n < N =Def p1·p2·p3…pn+1 → 仮定よりNは非素数、即ち合成数 Def. 完全数: 自身を除く全ての約数の和が元の数に等しい Ex. 6 = 1 + 2 + 3 Def. 過剰数: 元の数より大きい Ex. 18 < 1 + 2 + 3 + 6 + 9 Def. 不足数: 元の数より小さい Ex. 10 > 1 + 2 + 5 Def. 親和数: aがbの自身を除く全ての約数の和(vice versa) Ex. 220と284 Th. 素因数分解 factorization into prime numbers: 合成数は素数の積で表せる [一意性 uniqueness がある] エラトステネスの篩 Eratosthenes's sieve: N (∈ N)までの全素数の求め方 2の倍数(偶数)を消去 → 3の倍数を消去 → [√N]まで繰り返す(完了) [N]: Nを越えない最大の整数 (ガウスの記号 Gauss's symbol)
最大の素数: 2001年現在26972592 – 1 → メルセンヌ数(2M – 1)になる Ex. n, m ∈ Z, n ≡ m (mod d) ⇒ nとmがdを法として合同 ☛ フェルマーの最終定理 Fermat's Last Theorem |
|
geometry (geo = 土地, metry = 測量): 図形や空間の性質について研究 ユークリッド幾何学 Euclidean geometry: 5公理と5公準に基づく幾何学
初等幾何学 elementary geometry ⊂ ユークリッド幾何学 |
位相幾何学, トポロジー topology: 形を扱う数学分野
形(空間)を連続変形しても保たれる特性扱う → 一見無秩序な形中から秩序性見出し記述 Fractus (L): 「壊れる」という意味。複雑で手に負えないというニュアンス 代数幾何学 algebraic geometry: 代数的手法を用いた幾何学 |
5公理 (five axioms)Ax 1. 同一のものに相等しいものは、また互いに相等しいAx 2. 相等しいものに相等しいものを加えると、結果もまた相等しい Ax 3. 相等しいものから相等しいものを引けば、結果もまた相等しい Ax 4. 互いに相重なるものは相等しい Ax 5. 全体は部分より大きい 5公準 (five postulates)
Def. n次元ユークリッド空間: Rnに距離を定義 (否定公理系でも矛盾せず) = n本の軸が原点 origin で垂直に交わる空間 Def'. Rn := {(x1, x2, … xn)|xi ∈ R, i = 1, 2, … n},
a = (a1, a2, … an), b = (b1, b2, … bn) ∈ Rn ⇒ |
⇔ 非ユークリッド幾何学 non-Euclidean geometry
= 非Euclid公理: 別公理系幾何学 (≠ Euclid否定)
Th. 三角形の相似条件: ΔABC ∝ ΔA'B'C' 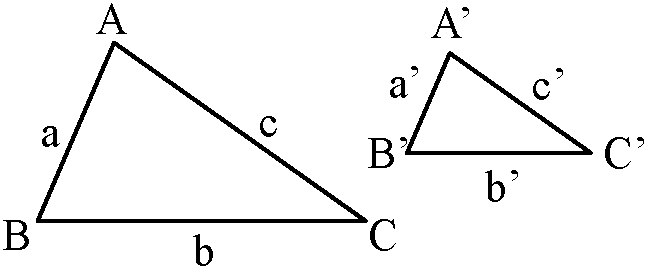
Def. トポロジー空間 topological space: 集合に要素同士の近さや繋がり方に関する情報を付け加えたもの → 要素の相対的な位置関係のみを扱う (位相幾何学: 柔らかい幾何学) Def. 円 circle: ある点(≡ 中心)から等しい距離(≡ 半径)にある点の集合Th. 円周角の定理 inscribed angle theorem: 円周角は同じ弧に対して一定 |
| 立体幾何学 (solid geometry) | ☛ 地図 |
|---|---|
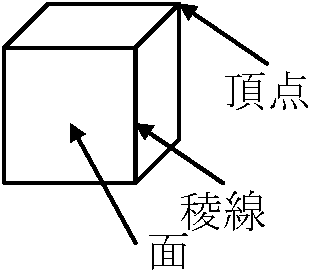 Def. 多面体: 有限個の点の凸包: 3次元空間内に点をばら撒き、それらの点を含む体積最小の凹みのない立体図形
Def. 多面体: 有限個の点の凸包: 3次元空間内に点をばら撒き、それらの点を含む体積最小の凹みのない立体図形Def'. 有限の半空間の共通部分: 3次元空間内を幾つかの平面で切り取った立体図形 頂点(頂上) vertex: 多面体の角 Def. 正多面体
= 正4面体、正6面体、正8面体、正12面体、正20面体 射影幾何学無限遠直線 ≡ 交わらない線が交わるように見える水平線
→ 全ての無限遠点は無限遠直線(水平線)を構成 正(直交)射影 orthogonal projection: 投影面に垂直な平行光線による射影 Th. 立体射影の3性質: 単位円 ≡ 単位直径1 (赤道 = WE = 1) → 半径 = 1/2 1. 緯度同じだが反対の緯度を持つ2つの地図上の互いに反転した2点に写す 1'. 球の赤道面に関する鏡映は地図の平面における反転に対応する Pr. 2点をP, Qとし、それぞれの緯度をα, -αとする。
Pr. [地図平面上の2曲線が∠α/で交わる → 球面上のそれらの像の曲線も∠α/で交わる → 射影は角を保つ] Th. メラネウスの定理 Menelaus theorem (平面)
(DA/AC)·(CB/BF)·(FE/ED) = 1
DA/AC = ED/GC, CB/BF = CG/FE (sinDA/sinAC)·(sinCB/sinBF)·(sinFE/sinED) = 1
sinDAは弧DAの中心角 |
ΔABC, π < ∠A + ∠B + ∠C < 3π Pr. ∠BAC = ∠EADとなる点Eをとる
→ ΔADC ∝ ΔABE, ΔADE ∝ ΔACB
→ 球面: (sinAD/sinDC)·(sinBC/sinAB) = (sinA'D'/sinD'C')·(sinB'C'/sinA'B') 立体投影法球: x2 + y2 + z2 = r2 (r ≡ 半径)球上の点P(x, y, z), 平面状の点Q(x', y', 0) →
x = 2r2x/(x'2 + y'2 + r2)
(cr + d)(x'2 + y'2) + 2ar2x' + 2br2y' – (cr + d)r2 = 0 ヘロンの公式: ΔABC, 各辺 a, b, c, 面積 a + b + c :=2s → 面積, S = √s(s – a)(s – b)(s – c) |
|
Def. 陽関数 explicit function: y = f(x)
x ≡ 独立変数 independent variable (引数 argument)
Ex. x2 + y2 = 1, xを与えた時本方程式を満足するy値は1つとは限らない Ex. x = t + 1, y = t2 → t消去可能: tを媒介変数とする表示 Def. 代数関数 algebraic function: f(x, y) = 0, f(x, y) → x, yの多項式
一般に陰関数 fn(x)yn + fn–1(x)yn–1 + … + f1(x)y + f0(x) = 0で表わせる
h(x) = a0 + a1x + a2x2 + … + anxn (an ≠ 0) (次数 G{h(x)} = n) h(x)/g(x) = h1(x)/g1(x) + h2(x)/g2(x) Def. 有理関数(有理型関数) f(x) = h(x)/g(x)で与えられる関数→ A/(x – a)k (実根) or (Lx + M)/[(x – p)2 + q2]k (虚根)とおける関数 Ex. (x + 1)/(3x3 + 2), (√5·x2 + π)/(ex) Def. 無理関数 irrational function ≠ 有理関数n乗根と四則演算から定義される関数 Ex. √x, (3√(x2 - 2) + 4)/(5x) 初等超越関数 elementary transcendental function≡ 代数関数ではない関数 Ex. 三角関数, 指数関数、対数関数初等関数 = 代数関数 + 初等超越関数 Def. limf(x) = l → l ≡ f(x)の極限値 or f(x)はlに収束 ⇔
∀ε > 0, ∃δ > 0, 0 < |x – a| < δ, ∀x ∈ D (変域) → |f(x) – l| < ε x: 指数 exponent, a: 底 base (表記法: y = ex, or y = exp(x)) a > 1 → 狭義単調増加, limax = +∞, limax = 00 < a < 1 → 狭義単調減少, limax = 0, limax = +∞ ∴ (-∞, +∞) continuous (指数関数の連続性) Case. x = 0 ⇒ lima1/x = limax = 1 Case. 00Def. 対数関数 logarithmic function: f(x) = y = ax (a > 0, a ≠ 1) → x = ay exist ⇒ logax (0, +∞) (a ≡ 底)
a = 10 → 常用対数 common logarithm |
logaxy = logax + logay (x, y > 0), logaxy = ylogax, loga1 = 0
a > 1 → 狭義単調増加, limax = -∞, limax = +∞ ∴ (0, +∞) continuous
Def. 冪関数 power function: f(x) = xα = aαlogax (x > 0) ⇒ Th. (0, +∞) ∋ xα, 単調連続関数 Def. 双曲線関数 hyperbolic function Def. 逆双曲線関数 inverse hyperbolic function
y = arcsinhx = log(x + √(x2 + 1)) … (1)
(1) x = sinhy = (ey - e-y)/2, ey = x ±√(x2 + 1) → y = log(x + √(x2 + 1)) → y = ±log√(x + √(x2 - 1)) ∵ (x + √(x2 - 1))(x - √(x2 - 1) = 1) // 弧度法 circular methodDef. 1ラジアン radian = 180°/π ≈ 57°.3' (180° = π radian) → 1° = π/180
l = rθ → θ = r/l → S = 1/2·r2θ → l上に点P(x, y)をとるとき Th. limx→0(sinx/x) = 1 Pr. 0 < x < π/2, 半径1の円で中心角xの扇形 ⇒ sinx < x < tanx
∴ cosx < sinx/x < 1 (0 < x < π/2) … (1) 三角関数公式 equations of trigonometric functionDef. 逆三角関数(三角関数の逆関数) inverse trigonometric functionEx. y = sinxの逆関数: y = sin-1x (⇔ x = siny) x[-1, 1] → yの値は無数 Def. 主値: y[-π/2, π/2] (一価にするため主値だけを考えることが多い) Ex. lim(sin-1x)/x A. y = sin-1x → x = siny, x → 0 → siny → 0 → y → 0
∴ lim(sin-1x)/x = limy/siny |
|
スカラー scalar (スカラー量 scalar quantity): 普通の数値で表す量
Ex. 温度、密度、気圧 → スカラー場 ベクトル vector (ベクトル量 vector quantity): 向きdirectionと大きさmagnitudeを持つ量Ex. 風、力、運動速度 → ベクトル場 ベクトル要素: ベクトルを構成するスカラー → ベクトルはスカラーの集合Def. Rの積集合Rnを考える(n個の積集合) → 元(x1, x2, …, xn): 元間に距離を定める 2点 X = (x1, x2, …, xn), Y = (y1, y2, …, yn)間の距離 := d(x, y)
d(x, y) = √Σ(xk – yk)2 (k = 1, …, n) ベクトル空間(ユークリッド空間) vector space平面や空間の幾何ベクトルの集まりDef. (幾何)ベクトル(geometric) vector: 方向と大きさを持つ線分 = 有向線分 Def. 2ベクトルは同じ方向と大きさを持てば等しい Def. 次元 dimension [dim ディム, ディメンション]
PAB < 180°, ベクトル系(a, b, c) → |a| = a12 + a22 + … + an2 = √Σi=1nai2 Def. ベクトル和 vector addition: 2ベクトル和= ベクトルの合成 composition of vectors
→ Def. 正規化 Def. 零(ゼロ)ベクトル, O: 大きさ0のベクトルDef. 逆ベクトル: a ⇒ a Def. 線形代数: A = (m, n), b: ベクトル → Ax = bをxについて解くこと Def. 線形結合(一次結合) linear combination: A∃x = b → ベクトルbが行列Aの列ベクトルの線形結合で表される 線形空間X上の有限個の元 x1, x2, …, xn → a1x1+a2x2 + … + anxn (ak ∈ K) → x1, x2, …, xnの線形結合 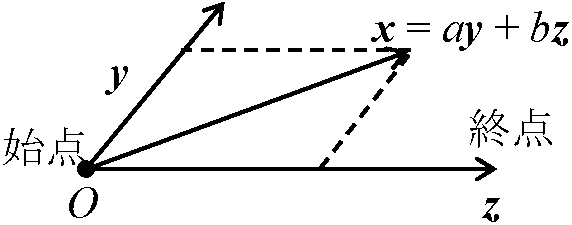 Def. 線形独立/従属(一次独立/従属): x, y, z, 1つのベクトルが他のベクトル線形和 (x = ay + bz, a, b = constant)
Def. 線形独立/従属(一次独立/従属): x, y, z, 1つのベクトルが他のベクトル線形和 (x = ay + bz, a, b = constant)→ ベクトル(x, y, z)は線形従属 linear dependent Th. 3ベクトルが同一平面上にある ⇒ 線形従属 Th. 3ベクトルが同一平面上にない ⇒ 線形独立 linear independent Th. a // b → 線形従属, a //[not] b → 線形独立 s.s. ax + by + cz = 0がa = b = c = 0のみ成立 → x, y, zは線形独立、a = b = c = 0以外で成立なら線形従属 Def. 「bは列ベクトルの張る空間(Aの列空間)にある」 →bがAの列空間にあれば唯一解か不定解存在 Th. 空間において4ベクトルは線形従属方程式が線形従属: 左辺 = ある式が他式を何倍かし加算 → 線形従属 → ベクトルの線形独立/従属と同 実際の連立方程式は規模大 → n次元(一般化): モデル化 → 解析 → 法則性Ex. → 解 → 線形性 x + 2y = 1, 2x - y = 0 → 唯一解がある x + 1/2·y = 1, 2x + y = -1 → 解けない = 不能 → 線形従属 x + 1/2·y = 1, 2x + y = 2 → 解けるが解複数 = 不定 → 線形従属 x + 2y = 1, 3x - y = -1, -x + y = 2 → 解なし(誤差最小解求める場合ある) x + 2y - z = 1, 2x + y + 2z = -1 → 未知数数 > 方程式数 → 不定解 x + 2y - z = 1, 2x + 4y - 2z = -1 → 未知数数 > 方程式数 → (暫定的に)不定解 → 線形従属 |
内分 m n 外分 ___●------------●--------●______←-------------------→ n ___A_______O_____B_____ ←----------→ ________________________O___m___A____B ________________________●------------●--------● Q. OA = a, OB = b, 線分ABをAからBへ向かってm:nに分ける分点をP → OP= xを線a, bの形結合で表せ A. [内分] AP = kBP [AP, BPは線形従属]
→ OP - OA = k(OB – OP) → x – a = k(b – x) 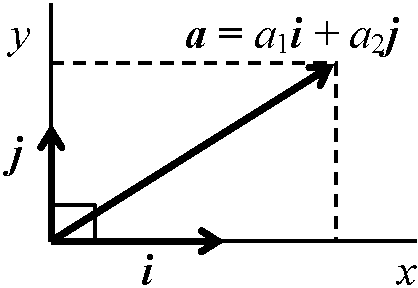
= i, jの線形結合として一意的に決まる] 内積 dot product, inner product= スカラー積 scalar product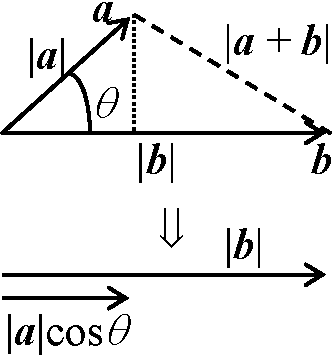 Def. 内積 a·b or (a, b) = |a||b|cosθ, θ:: aとbのなす角
Def. 内積 a·b or (a, b) = |a||b|cosθ, θ:: aとbのなす角
0 < (a, b) → 0 < θ < 90°
= a1a1 + a2a2 + … + anan = a12 + a22 + … + an2 Def. aのノルム(規格) norm: ||a|| ≡ この内積で表わされるAの大きさ|a|Ex. ||a|| = |a| = √(a, a) = √(a12 + a22 + … + an2) Def. a = (a1 + a2 + … + an), b = (b1 + b2 + … + bn) →a·b = a1b1 + a2b2 + … + anbn = Σi=1naibi Th. a ≠ 0, b ≠ 0 → cosθ = (a·b)/|a||b| = Σi=1naibi/√Σi=1nai2√Σi=1nbi2Ex. 3次元: cosθ = (a1b1 + a2b2 + a3b3)/{√(a12 + a22 + a32)√(b12 + b22 + b32)} Ex. a = (1, 1, 1 ), b = (1, 2, 3)
内積 → (a, b) = 1 + 2 + 3 = |a||b|cosθ = 6 → 2 Pr. LS2 - RS2 = ((a + b)/2)2 - (√(ab))2 = (a2 + 2ab + b2)/4 - ab = (a2 -2ab - b2)/4 = (a - b)2/4 ≥ 0 // Th. 三角不等式(シュワルツの不等式): a·b ≤ |a||b|, 等号成立 cosθ = 0Pr. a·b = |a||a|cosθ ≤ |a||b| 外積 cross product= exterior product, or outer product (ベクトル積 vector product)空間理論で重要 Def. 外積 outer product, a×b = |a||b|sinθ
a×bは180°より小さい角を通りaからbへ右ネジを回すと進む向き 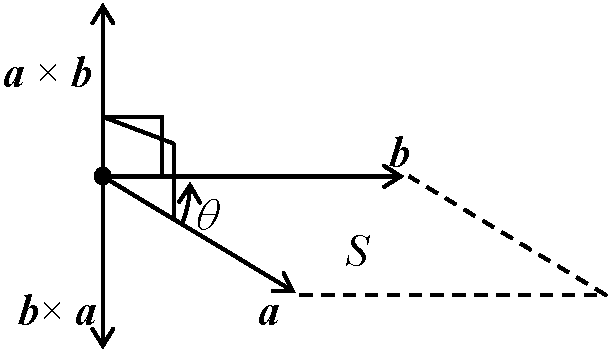 Th. 外積の大きさはa, bの作る平行四辺形の面積(S)に等しい
Th. 外積の大きさはa, bの作る平行四辺形の面積(S)に等しい
a = 0, b = 0 or a // b → a × b = 0 Pr. trivialTh. 外積ベクトルa×bは、それぞれのベクトルa, bに垂直である Law
a×b = (b1c2 – c1b2, c1a2 – a1c2, a1b2 – b1a2) = → sinθ = |a×b|/(|a||b|) = √{(a2b3 – a3b2)2 + (a3b1 – a1b3)2 + (a1b2 – a2b1)2}/ {√(a12 + a22 + a32)·√(b12 + b22 + b32)} ⇒ 固有値と固有ベクトル |
|
Def. ホモロジー homology: 空間や代数的対象の"穴"を代数的に測る仕組み Def. ホモロジー球面 homology sphere: そのホモロジー群がn次元球面Snと同型な閉多様体 基本群(ポアンカレ群) Def. ホモトピー homotopy: fをgに連続的に変形する「道」
可縮空間: 1点と同じホモトピー型を持つ空間
無限遠のところで単連結な可縮多様体はn次元空間のみ
自身と交わらない閉じた曲線
⇒ 補集合 R2\C - 2つの連結成分に別れる → それぞれを定義 Def. 外側 exterior: 無限に広がる unbounded, 連結, 曲線の外側にある領域 Def. 境界: 内側と外側の境界は同じ曲線 C ∵ ∂Uint = C = ∂Uext |
Th. ブローウェルの不動点定理 Brouwer fixed point theorem ユークリッド空間の閉球からそれ自身への全ての連続函数は不動点を持つ ☛ (3次元)ポアンカレ予想単連結な3次元閉多様体は3次元球面S3に同相 ⇒⇒ (同値) 3次元ホモトピー球面はS3と同相
一般化(n次元に拡張): n次元ホモトピー球面はSnと同相 |
[ 組合わせと順列 ]
|
Def. 基準数列, I = a1 < a2 < … < anなる数列 Def. 転倒: 2つの数字の並びがIとは逆になっていること Ex. 1, 2, 4, 3 → 1, 3, 4, 2 → 2個の転倒(3-2, 4-2間) Th. 転倒の個数と入れ換えの回数は等しい
a) 3, 7, 2, 5, 1, 6, 4 → 11個の転倒
Def. 順列 i1, i2, …, inの符号 ε(i1, i2, …, in) = -1, or 1 Th (拡張). (i1, i2, …, in) →
ε(i1, …, ij, …, ik, …, in) = -ε(i1, …, ik, …, ij, …, in) 2) k > j + 1 → i1, …, ik, …, ij, …, inは
i1, …, ij, …, ik, …, inからijを右へ(k – j)回、相隣り合う入換えを行う 行列式 (determinant)Def. n次正方行列 A = (aij), 自然数(i, j, k)
→ n2個成分aijから作られるΣεij…ka1ia2j … ankなる式
次の行列式 |aij| = a11 2次の行列式 |aij| = Σεija1ia2j = a11a22 – a12a21 3次の行列式 |aij| = Σεijka1ia2ja3k = e123a11a22a33 + e132a11a23a32 + e213a12a21a33 + e231a12a23a31 + e312a13a21a32 + e321a13a22a31 = a11a22a33 – a11a23a32 – a12a21a33 + a12a23a31 + a13a21a32 – a13a22a31 Def. 行列式の展開: 右式を求めること → 展開式 = 右式
Ex.
Def. 余因数 (余因子 cofactor): 小行列式に符号をつけたもの → A-ij = (-1)i+jAij, or aijAij (n次正則行列で成立) Th. 余因数展開定理: 余因数を用い行列式を展開すること(行列式はある行(列)について余因数展開可能) ⇔ A = Σj=1naijAij, or Σi=1naijAij≡ 行列式は、任意の行(列)の要素とその余因子の積の総和に等しい Pr. (1次: Def.よりtrivial) 2次: a1α·a2β, R = (αβ) → (R) = +1 偶行列, -1 奇行列
Ex. A = 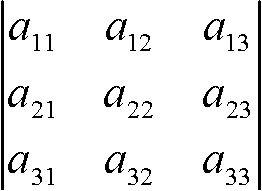
= a11a22a33 + a12a23a31 + a21a32a13 – a13a22a31 – a12a21a33 – a11a23a32 R = (αβγ) → (R) = +1 偶行列, -1 奇行列 n次: n2個の数を正方形に並べる
A = → (R) = 1: 偶行列, = -1: 奇行列
= a11(a22a33 - a23a32) + a12(a23a31 - a21a33) + a13(a21a32 - a22a31) … (2)
(2) 1行の要素での一次式 → 同様に2-3行, 1-3列の各要素でも作れる + a23(a12a31 - a11a32) ___ 2行 a13(a32a21 - a22a31) + a23(a12a31 - a11a32) + a33(a11a22 - a12a21) ___ 3列
1行の要素(A1) : A1 = = a11A11 + a12A12 + a13A13 … (3)
2行の要素(A2): A2 =
= a11A11 + a12A12 + a13A13 (1行)
Th. ある行(列)の要素に他の行(列)の要素の余因数をかけ加えると零 ⇒ Σi=1naij·Aik = Σi=1naji·Aki = 0 (j ≠ k)
a11A12 + a21A22 + a31A32 = 0
a11A21 + a12A22 + a13A23 = 0
= 行列式の性質(定理)1. 転置行列式(行と列を交換した行列式)の値はもとの行列式の値と等しい→ |A| = |A'| Pr. k列で余因数展開 |A'| = ak1A'1k + ak2A'2k + … + aknA'nkA'ik = Aki → ak1A'1k + ak2A'2k + … + aknA'nk = ak1A'1k + ak2A'2k + … + aknA'nk = |A| Th. 行について成立つことは、列についても成立 2. 交代性: 2つの行(列)を入換えると符号が変わる
Ex. A =
ε(i1, …, ij, …, ik, …, in) = -ε(i1, …, ik, …, ij, …, in) Pr. trivial 4. 2つの行(列)の対応する要素が相等しい → |A| = 0 Pr. その相等しい行列を入れ換えると性質2により符号が変わる → D = -D, 2D = 0 ∴ D = 0 5. 多重線形性 (複線形性, multi linearity) (1)行列式Aは1行(列)をm倍すると値はmAとなる
Ex. m – ma12a21a33 – ma11a32a23 = (ma11a22a33 + a12a23a13 + a13a32a21 – a13a22a31 – a12a21a33 – a11a32a23) = (左辺) // Ex. |(a1, …, map, …, an)| = m|(a1, …, ap, …, an)|, 1 ≤ m ≤ n |
6. 多重線形性 (2) 1つの行(列)の各要素が2数の和になる行列式の値は、始めの数をその行(列)に置換えた行列式と後の数をその行(列)に置換えた行列式の和に等しい
Ex. = |(a1, …, ap, …, an)| + |(a1, …, aq, …, an)| 7. 1つの行(列)の各要素をm倍して他の行(列)の対応する要素に加えても行列式の値は変わらない
Ex. |(a1, …, ap + maq, …, aq, ···, an)| = |(a1, …, ap, …, aq, …, an)| + |(a1, …, maq, …, aq, …, an)|
第2項は0 8. 三角行列式の値は、主対角線の元の積に等しい
Ex.
= (a - b)(b - c) 連立方程式 simultaneous equationDef. 連立1次方程式 Ax = b2つ以上の方程式の未知数が同一の値をとるときの方程式の組 a11x1 + a12x2 = b1a21x1 + a22x2 = b2 A. 代数的解法 1) a11/a21 = a12/a22 ≠ b1/b2 [不能] 解存在しない* 2) a11/a21 = a12/a22 = b1/b2 [不定] 解無数* * 比例式では分母が0の項については分子も0と考える(規約) 3) a11/a21 ≠ a12/a22 → a12a21 – a11a22 ≠ 0(a11a22 – a21a12)x1 = b1a22 – b2a12 → x1 = (b1a22 – b2a12)/(a11a22 – a21a12) (a11a22 – a21a12)x2 = a11b2 – a21b1 → x2 = (a11b2 – a21b1)/(a11a22 – a21a12) Th. クラメール Cramer (スイス)の公式:D =
(上の)連立1次方程式の解 [x1, x2が0以外の解を持つ] Th. 連立一次方程式 simultaneous linear equation, SLE:a11x1 + a12x2 + a13x3 = 0, a21x1 + a22x2 + a23x3 = 0 を満たすx, y, zの比 → x:y:z = Pr. x3: 既知 → a11x1 + a12x2 = -a13x3, a21x1 + a22x2 = -a23x3 とすれば前問に戻る D =x1 = D12/D , x2 = D22/D → x1 =x2 = Th. クラメールの公式: n次に拡張 → 未知数をn個含む連立方程式 a11x1 + a12x2 + … + a1nxn = a1 a21x1 + a22x2 + … + a2nxn = a2 … an1x1 + an2x2 + … + annxn = an Dn = 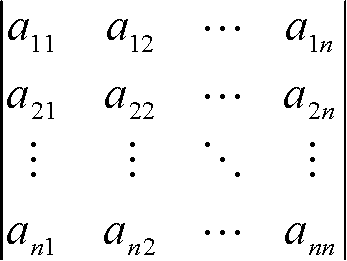 , , Dnx1 = Dn1, Dnx2 = Dn2, …, Dnxn = Dnn , , Dnx1 = Dn1, Dnx2 = Dn2, …, Dnxn = DnnDn ≠ 0 → xk = Dnk/Dn (k = 1, 2, 3 … n) [Cramerの公式] ⇒ Th. a) Dn = 0 → x1 = x2 = … = xn = 0 ⇒ Th. b) Dn ≠ 0 → x1 = x2 = … = xn = 0以外の解を持つ Pr. n次行列 A = (aij)の列(行)ベクトルをa1, a2, …, an
c1a1 + c2a2 + … + cnan = 0 Def. a1 = a2 = … = an = 0 → Ax = 0 ≡ 連立1次同次方程式 Def. 基本解: 連立1次方程式の解ベクトルのなすベクトル空間の元 Def. 一般解: 基本解の1次結合 ≡ 特殊解 + (n – r)個の基本解 Def. 2次の行列式の積:
AB =
= → a(A + B) = aA + aB, (a + b)A = aA + bA, a(bA) = abA Pr. A = aij, B = bij→ a(aij + bij) = aaij + abij, (a + b)aij = aij + bij, a(baij) = abaij 終結式 resultant= 消去式 eliminant (今、使う人はいない)f(x) = a0x2 + a1x + a2 = 0 g(x) = b0x3 + b1x2 + b2x + b3 = 0___(a0b0 ≠ 0)
共通根 x を出す条件を探す = (cA)x = 0x = 0
∴ (c1x2 + c2x + c3)f(x) + (c4x + c5)g(x) = 0
Case. c4 ≠ 0: {α1, α2, α3, α4} = {β1, β2, β3, β4} いずれもα1, α2とβ1, β2, β3との間に等しいもの(共通根)が存在 [拡張] 一般にf(x) = a0xm + a1xm-1 + … + am = 0 g(x) = b0xn + b1xn-1 + … + bn = 0___(a0b0 ≠ 0) に対して
R(f, g) = R(f, g) = 0 Sylvesterの消去法: f(x), g(x)よりR(f, g)を求める計算Gaussの前進消去: 連立方程式が線形従属なのか知る方法
左辺の係数が全て0になる方程式が1つでも発生したら線形従属 |
行列式とは全く異なる!
|
行列: 「ベクトルのベクトル」を考えたのが行列(ベクトルは行列の真部分集合) Def. m行(row) n列(column)の行列, m × n(型の)行列, (m, n)(型の)行列
m × n個の数aijを長方形に並べたもの Def. 行: 第i行 = (ai1, ai2, …, ain) (aijは式・関数もある) Def. 成分(要素): aijをAの(i, j)成分(要素)
Def. 実行列: 成分が全て実数の行列 Def. m = n ⇒ 正方行列 square matrix (n × n ⇒ n次正方行列) Def. 対角成分 ≡ akk (k = 1, 2, … n) Def. 上(下)三角行列: A (上) =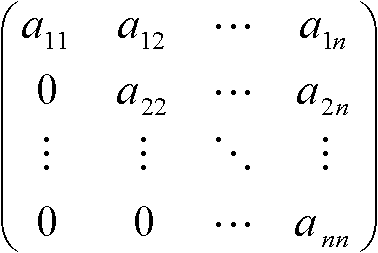
→ 正方行列 A = (aij), i > j → aij = 0 (or i < j → aij = 0) Th. 三角行列 ⇒ 和、差、積は三角行列Def. 対角行列 diagonal matrix: 正方行列 A = (aij), i ≠ j → aij = 0 Def. トレース trace: n次正方行列 A → 対角成分の和, trA or tr(A) = a11 + a22 + … + ann = Σi=1naii Def. (m, n)行列, A = (aij), B = (bij), C = (cij) →
相等: ∀ij, aij = bij → A = B Pr. 1. A + B = (aij + bij) [数に関し交換法則成立] = (bij + aij) = B + A Pr. 1'. A + Bのij元はaij + bij, B + Aのij元はbij + aij
数の加法に関し交換法則が成立 aij + bij = bij + aij ((aij + bij) + cij) = (aij + (bij + cij)) [数に関し交換法則成立] = A + (B + C) Pr. 2'. (A + B) + Cのij元は(aij + bij) + cij
A + (B + C)のij元はaij + (bij + cij) [数に関し加法に関し結合法則成立] Pr. A + 0 = (aij + 0ij) = (aij) = A, 0 + A = (0ij + aij) = (aij) = A Th. 加法の逆行列: A = (aij), X = (xij), 0 = (0ij), A + X = 0 → X = -A Pr. aij + xij = 0ij = 0 → X = (-aij) = -A Th. 移行: A = (aij), B = (bij), X = (xij), A + X = B → X = B + (-A), X = B – A Pr. aij + xij = bij → xij = bij - aij 実数と行列の積(スカラー倍)(m, n)行列, A = (aij), a ∈ ℜ →Law. 分配法則: a(A + B) = aA + aB, (a + b)A = aA + bA Pr. A = (aij), B = (bij) (aij + bij) = aaij + abij (∵ 数字について分配法則成立) ∴ a(A + B) = aA + aB [別解: 元で解く]< (a + b)aij = aaij + baij (∵ 数字について分配法則成立) ∴ (a + b)A = aA + bA Law. 交換法則: Aa = (aija), aA = (aaij) [-A = (-1)A]Pr. A = aij, a(baij) = abaij [数字については積の順序は問わない] ∴ a(bA) = abA Q. A = aij, B = bij, C = cijの各成分が次のように与えられているとき、
3A − 2B + Cを求めよ d11 = 1, d12 = 11, d13 = −1, d21 = −9, d22 = 5, d23 = 10 Th. (m, n)行列 A, 実数 a, b → a(bA) = abAPr. A = aij, a(baij) = abaij 行列の積 multiplying matricesDef. (m, n)行列 A = (aij), (n, l)行列 B = (bjk), AB = C
→ cij = Σs=1naisbsjが(ij)となるCをABの積
= 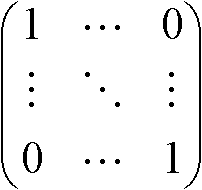
AE = A: 行列式をとると値は必ず 1
δij = 1 (i = j), or 0 (others) A. AB = Def. AB ≠ BA ⇒ 非可換 = 乗法交換法則不成立 Def. AB = BA ⇒ 可換(交換可能) P ≠ 0, Q ≠ 0, PQ = 0 (積が零行列となることがある) ⇒ Def. P, Q: 零因子 zero divisor, or nil factor Ex. A =Q. A2 = BA = Th. 1. 交換法則 (AB)C = A(BC) Th. 2. 分配法則 A(B + C) = AB + AC, (B + C)A = BA + CA Th. 3. (Aa)B = A(aB) = a(AB), a ∈ ℜ Pr. A = (aij) (m, n) 行列, B = (bij) (l, k), C = (cij) (l, k) Pr. 1. AB = (αij) = Σs=1naisbsj (m, l), BC = (βij) = Σt=1lbitctj (n, k), 証明すべき式の両辺は共に(m, k)行列 |
(AB)Cの(i, j)元は Σt=1laitctj = Σt=1l(Σs=1naisbst)ctj
= (Σs=1naisbs1)c1j + (Σs=1naisbs2)c2j + … + (Σs=1naisbsl)clj
+ (ai1b12 + ai2b22 + … + ainbn2)c2j + …
= ai1(Σt=1lb1tcij) + ai2(Σt=1lb2tcij) + … + ain(Σt=1lbntcij) Pr. 3. Aa = aaij , (aaij)B → (Aa)Bの(i, j)元: aΣi=1naijbij _aB = abij, A(abij) → A(aB)の(i, j)元: aΣi=1naijbij// Def. 転置行列 transposed matrix, A': A = (m, n) → A' = (n, m)
Ex. A = 1. (A')' = A → もう一度転置するともとに戻る (Pr. Trivial //) 2. (A + B)' = A' + B' Pr. (m, n)行列 A = (aij), B = (bij), A + B = (cij) → A + B = (aij) + (bij) = (aij + bij) ∴ (A + B)' = A' + B' 3. (kA)' = kA' (Pr. Trivial //)4. (AB)' = B'A' Pr. (m, n)行列 A = (aij), (n, l)行列 B = (bij), AB = C, B'A' = D
Aの(i, j)成分 aij = Σk=1naikbkj → (AB)'の(i, j)成分 cij = Σk=1najkbki (n, n), A = (aij), A = A'のときのA Ex. A = A', 任意の行列Tに対しT'ATは対称行列A. (T'AT) = (AT)'·(T')' = T'·A'·T = T'AT (A' = A) ∴ T'AT = 対称行列 // Def. 交代行列 skew symmetric matrix: [対角成分は全て0] (n, n), A = (aij), A = –A'のときのA 位(階級, 階数, ランク) rankDef. (m, n)行列 A = (aij) =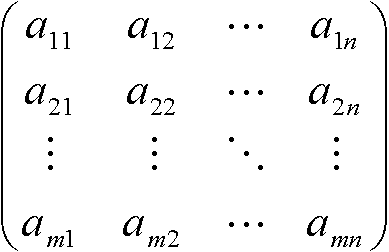 r次行列式中に少なくとも1つ0でないものがあり、(r + 1)次の行列式が全て0 → 行列の位(階級, ランク) rankはr、記号でR(A) or Rank(A) = rと書く Eq.: 2-4 = 行(列)基本変形
Th. R(AB) ≤ min(R(A), R(B)) Th. A = (m, n), B = (m, m), C = (n, n) ⇒ R(BA) = R(A) = R(AC) Th. 係数行列の階数 ≠ 拡大係数行列の階数 ⇒ 方程式は解をもたない 逆行列 inverse matrixDef. 正則行列 regular matrix (non-singular matrix)正方行列(n, n), A = (aij), AX = XA = E, X exist → 行列A ≡ 正則行列 Th. |A| ≠ 0 → Aが正則行列である必要十分条件Pr. AX = EなるX存在 → |AX| = |A||X| = |E| ∴ |A| ≠ 0 Def. 逆行列 X ≡ A-1 → AA-1 = A-1A = E, A-1 = (1/|A|)·A~ Def. 特異行列 singular matrix: 逆行列を持たない行列 Ex. 2次: A =A.
x + 2y = 1, 3x + 5y = 0, u + 2v = 0, 3u + 5v = 1
Ex. A = Th. Aの逆行列が存在するなら唯一である Pr. Aの逆行列が存在したとする。それらをX, Yとすると
AX = XA = E, AY = YA = E,
→ A-1 =  → A' → → A' →
|A| = 1, A11 = (+1) × 正則行列Aにおける(A, I) → 基本変形 → (I, A-1) [逆も真] 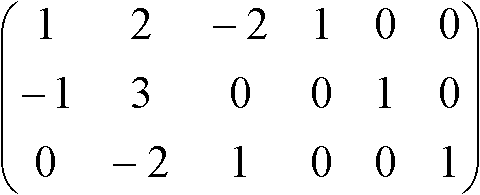 = = 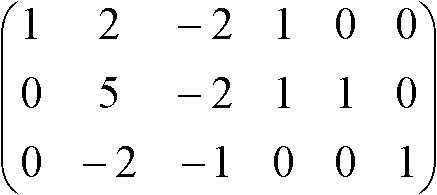 = 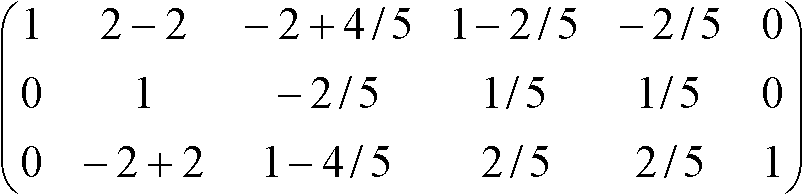 = 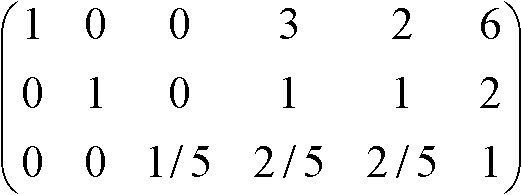 → 当然ながら解は上記 → 当然ながら解は上記Th. (AB)-1 = B-1A-1 Pr. ABB-1A-1 = AIA = AA-1 = I Th. (A-1)1 = (A1)-1 Pr. (A-1)1 = A-1 = (A1)-1 |
|
座標 coordinates:
n次元空間の点(P)はn個の実数からなる組で表される 座標 P(x1, x2, …, xn) → 座標系 coordinate system: この対応関係全体
__C____O(A)________P 一次元Def. 直線 line (cf. 零次元: 点 point)
Def. 座標系: P ⇔ F 一対一の対応 ⇒ この対応 = 座標系
xを点Pの座標といいP(x)とかく: OP = x Th. CP = –PC Pr. CP = CO + OP = –OC – PO = –(OC + PO) = –(PO + OC) = –PC Def. 距離 (方向線分の長さ): 点 A, B → |AB| Th. 一直線上の3点 O, A, B → 3点の位置如何に関わらず AB = OB - OA Pr. A(a), B(b)とすると OA = a, OB = b → AB = b – a = OB – OA Th. 1直線上にn点(P1, P2, …, Pn-1, Pn) → 点の位置如何に関わらずP1P2 + P2P3 + … + Pn-1Pn = P1Pn成立 Pr. P(x1), P(x2), P(x3), ..., P(xn-1), P(xn)とおくと(左辺) = (x2 - x1) + (x3 - x2) + ... + (xn - xn-1) = xn - x1 = (右辺) 二次元平面 plane 上の点の位置と数で表す方法
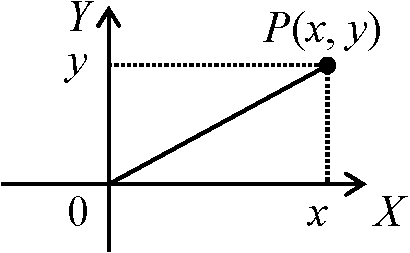
P → (A, B) → (x, y) ⇔ (x, y) → (A, B) → P 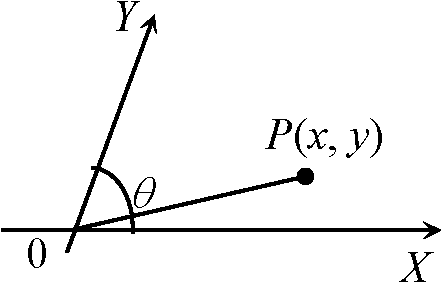
P → (A, B) → (x, y) ⇔ (x, y) → (A, B) → P
(r, θ) → Pは一意的に決まる 三次元三次元点の位置を数で表す方法1) 直交座標 (直交軸) → 直交座標系: (x, y, z) ≡ 点Pの直交座標
各象限の正負を考える
x = x座標, y = y座標, z = z座標, OX = x軸, OY = y軸, OZ = z軸 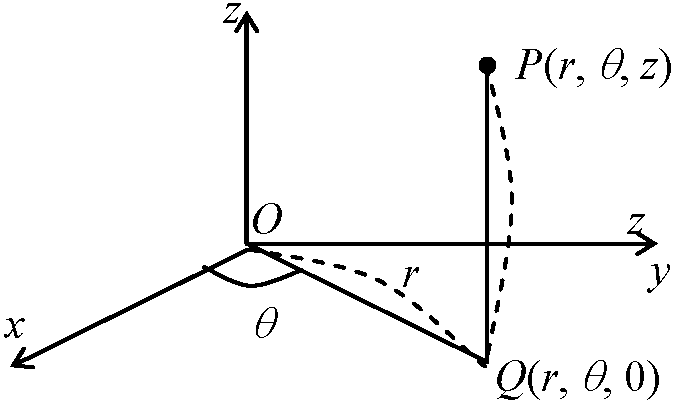 3) 円柱座標
3) 円柱座標円柱座標 = (r, θ, z) → Pは一意的に決まる ⇔ P → (r, θ, z)は一意的に決まらない
(一意的にするための)制限 r ≥ 0, 0 ≤ θ < 2π or –π ≤ θ < π 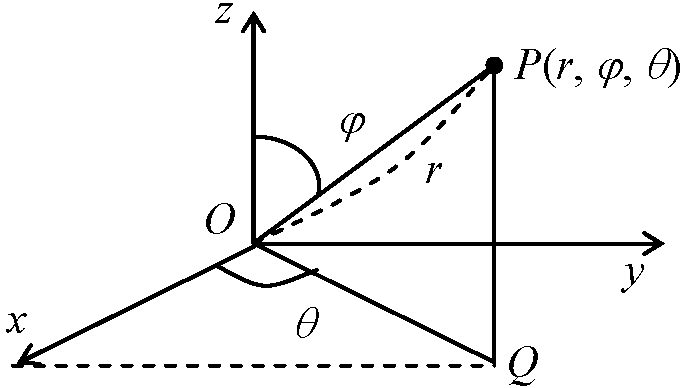 4) 極座標
4) 極座標極座標(r, θ, φ) → P一意的に決まる ⇔ P → (r, rcosθ, rsinθ)は一意的に決まらない
制限: r ≥ 0, 0 ≤ θ ≤ φ, 0 ≤ θ < 2π r: 動径, rcosθ: 天頂角, rsinθ: 方位角 直交座標との関係: 極座標(r, θ, φ) → 直交座標(x, y, z)
x = OQcosθ = rcos(π/2 – φ)cosθ = rsinφcosθ, ∴ r = √(x2 + y2 + z2) 次にx2 + y2 = r2sin2φ(cos2θ + sin2θ) = r2sin2φ ∴ rsinφ = √(x2 + y2) Q. 二次元斜交軸に対し 1) x = a, 2) y = b, 3) y = x,4) x2 + y2 + 2xycosθ = r2 の表す図形を書け A. 1-3) Q. 直交座標が a) (√2, √2), b) (1, √3), c) (-√3, -1), d) (-3, -3) の極座標を求めよ A. a) r = √(2 + 2) = 2, θ = tan-1((2/(2) = tan-1(1) = π/4 ∴ (2, π/4) b) r = 2, θ = tan-1√3 = π/3 ∴ (2, 3/π) c) r = 2, θ = tan-1((3) - 1 = 30°, 210° この場合210° ∴ (2, 210°) d) r = √(x2 + y2) = 3, θ = tan-1(x/y) = π/4 and 5/4·π この場合5/4·π ∴ (3, 5/4·π) Q. 極座標が(√2, π/4)の直交座標を求めよA. x = rcosθ, y = rsinθ。x = √2·sin(π/4) = 1, y = √2·cos(π/4) ∴ (1, 1) Q. 2次元極座標系: 1) r = 5, 2) rcosθ = 3, 3) rsinθ = 2, 4) r = 4cosθ, 5) r = 4sinθの表す図形を書け Q. 3次元斜交軸で 1) x = y = z, 2) x = y, z = 0, 3) x = y の表す図形を書けA. 1)-3) A. x = rcosθ, y = rsinθ, z = z (2cos(π/6), 2sin(π/6), -2) = (2·√3/2, 2·1/2, -2) = (√3, 1, -2), (0, 3, 1), (2, 2√3, -3) Q. 直交座標が a) (1, 0, 0), b) (1, -√3, 2), c) (√3, -1, 5)なる点の円柱座標A. a) r = √(x2 + y2), θ = tan-1(y/x), z = z ∴ (√(12 + 02), tan-10, 0) = (1, 0, 0) b) (√(1 + 3), tanθ-1(-√3), 2) = (2, 300°, 2) c) (√(3 + 1), tan-1(-1/√3), 5) = (2, 330°, 5) Q. 極座標が(4, θ/3, θ/6, 2), (2, θ/2, θ/3)なる点の直交座標を求よ A. x = rsinφcosθ, y = rsinφsinθ, z = rcosφ
x = 4sin(π/3)cos(π/6) = 4(√3)/2·√3/2 = 1, A. r = √(x2 + y2 + z2), φ = tan-1(√(x2 + y2)/z), θ = tan-1(y/x)
a) r = √(1 + 3 + 4) = 2√2, φ = tan-1(√(1 + 3)/2) = tan-11 = π/4, θ = tan-1(3/1) = π/3 ∴ (2√2, π/4, π/3)
A. a), b), c) 省略
a) θ = 0, z = 0 の表す図形を書け A. 1), 2), 3) 省略4) r = rcosθ, r2 = 4rcosθ (r2 = x2 + y2, rcosθ = x), x2 + y2 = 4x ∴ (x -2)2 + y2 = 4 球(面)1点Cからの距離が一定値rである点Pの集合 ⇒ |CP| = r平面: 円 (z = 0), 立体: 球面  r = √(x2 + y2 + z2), r2 = x2 + y2 + z2,
r = √(x2 + y2 + z2), r2 = x2 + y2 + z2,
θ = π/4,
r = 2acosφ,
r2 = 2arcosφ, r2 = x2 + y2 + z2, r = a → x2 + y2 + z2 = a2 → 中心を極(0, 0, 0)とし半径aの球 基準面に垂直な曲線: r2 = 2arcosφ ∴ x2 + y2 +(z - a)2 = a2→ 中心を(0, 0, a)とし半径aの球 Th. アポロニウスの円: 平面上の2点から距離の比が一定な点の集合 ⇒ 円Q. xyz空間, 2点A(1, 1, 3), B(-2, 4, -1), AP:BP = 2:1 → 点Pの軌道 A. P := (x, y, z) → OP = (x, y, z)
|AP| = 2|BP| ∴ |AP|2 = 4|BP|2 → (成分表示) 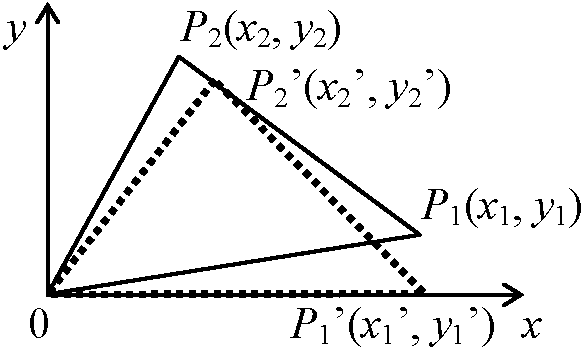
極座標変換 OP1→ → OP→, S = 1/2·x1'·y2' (ただし絶対値) Def. 正射影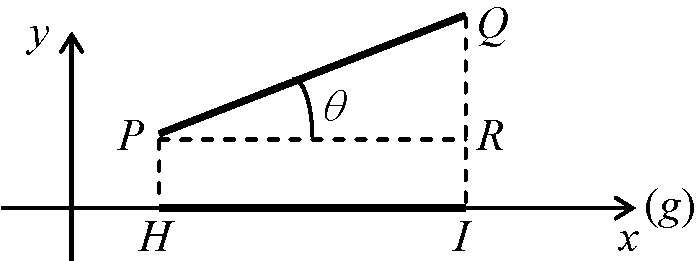 点Hを点Pの直線g上への正射影 + HIを線分PQの直線g上への正射影という HI = PR = PQcosθ H1H2 + H2H3 + … + Hn-1Hn = H1Hn∴ P1P2cosθ1 + P2P3cosθ2 + … + Pn-1Pncosθn-1 = P1Pncosθn ⇒ Th. 接線の各線分の一直線上への正射影の和は接線の始点と終点を結んだ線分の同一直線上への正射影の大きさに等しい 有効直線の方向比と方向余弦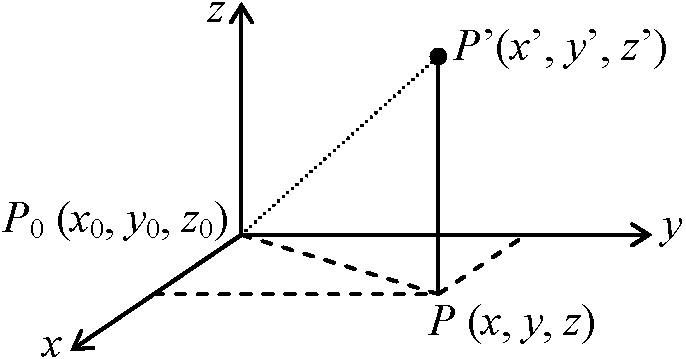 P0, Pを対角線とする直方体 + P0, P'を対角線とする直方体 Def. 方向比 direction number, u:v:w = x – x0:y – y0:z – z0とおいたもの (u1, v1, w1) →
(u2, v2, w2): 反対向きに平行 u1:v1:w1 = –u3:– v3:–w3 |
 x – x0:y – y0:z – z0 = cosα:cosβ:cosγ
x – x0:y – y0:z – z0 = cosα:cosβ:cosγcosα = (x – x0)/r, cosβ = (y – y0)/r, cosγ = (z – z0)/r ∴ x – x0:y – y0:z – z0 = cosα:cosβ:cosγ 左辺は有効直線の方向比。従って右辺も有効直線の方向比 Def.方向余弦 direction cosine: 方向ベクトル p = (u v w)の各成分 u, v, w
方向余弦の方向とx, y, z軸の正方向とのなす角をα, β, γ ⇒ Pr. u2 + v2 + w2 = cos2α + cos2β + cos2γ = 1/r2{(x – x0)2 + (y – y0)2 + (z – z0)2} = r2/r2 = 1 同じ向きに平行 l1 = l2, m1 = m2, n1 = n2反対向きに平行 l1 = -l2, m1 = -m2, n1 = -n2 2点の方向比と方向余弦A = (l, m, n), B = (u, v, w) → AB = (u - l, v - m, w - n) ⇒
距離, k = √(u - l)2 + (v - m)2 + (w - n)2)
方向ベクトル a = (l, m, n), b = (u, v, w) → a ⊥ b (θ = 90° or π/2) ⇔ lu + mv + nw = 0 点と直線の距離Ax. A(a)を通り単位方向ベクトルeの直線gとB(b)との距離h (≥ 0)h = √(|b - a|2 - ((b - a)·e)2) Pr. Bからgに下した垂線の足をC → △ABCは直角三角形h2 = AB2 - AC2 (ピタゴラスの定理)
= AB2 - (AB·cosθ)2 = |b -a|2 - (|b -a|·cosθ)2 A. C(u, v, w): Bからgへ下した垂線の足の座標 BC ⊥ g → u (gの方向ベクトル) = (3, 2, 2)に対しBC·u = 0 → 3(u -1) + 2(v - 1) + 2(w -2) = 0
Cはg上 → (u - 2)/3 = (v - 1)/2 = (w + 2)/2 u = 3t + 2, v = 2t + 1, w = 2t - 2
t = 5/17 → u = 49/17, v = 27/17, w = -24/17 (x - x0)/l = (y - y0)/m = (z - z0)/n = t (媒介変数) → Def. 媒介変数表示: x = x0 + tl, y = y0 + tm, z = z0 + tn Q. x軸となす角αが45°、y軸となす角βが60°であるこの直線のz軸となす角γ A. cos2α + cos2β + cos2γ = 1,
cos45° = cos(π/4) = 1/√2, cos60° = cos(π/3) = 1/2 1次形式 linear form or one-formDef. 1次形式 (≡ 線形関数): f(x1,x2,…,xn) = a1x1 + a2x2 + … + anxnDef. 双1次形式 (双線形形式, 双一次関数) bilinear form f(x, y) = txAy, A = (m, n) Th. (1) 定正値な双1次形式φ(x, y)が定義されたベクトル空間Vはユークリッド的空間にでき、その逆も成立Th. (2) 定正値な双1次形式φ(x, y)の基e1, e2…enに関する行列A ⇒ |A| > 0 2次形式 quadratic formDef. p, q, r ∈ ℜ, X, Yの同次2次式 ⇒F(x, y) = pX2 + 2qXY + rY2 ≡ 2次形式 F(x, y) >(<) 0 ((X, Y) ≠ (0, 0)) ≡ 正(負)定値 Th. 正(負)定値の判別: F(x, y) = pX2 + 2qXY + rY2 (2次形式) ⇒
(1) p > 0, pr - q2 > 0 ⇒ F(x, y) ≡ 正定値 F(x, y) = p(X + q/p·Y)2 + (pr - q2)/p·Y2 ≥ 0 等号はX + q/p·Y, Y = 0 → X = Y = 0の時に成立
(2) (1)と同様
F(1, 0), F(q, -p)は異符号 → F(x, y)は正値と負値をとる Case. p = 0 → pr - q2 < 0, q ≠ 0 ∴ F(X, 1) = 2qX + r // Th. φ(x, x)をn次元ベクトル空間Vで定義された2次式Vの適当な基e1, e2, … enを選んで φ(x, x) = λx12 + λ2x22 + … + λnxn2 とできる。ただし、x = x1e1 + x2e2 + … + xnen Def. 2次形式の標準形: φ(x, x) = λx12 + λ2x22 + … + λrxr2 (r ≤ n)r: 行列Aの階数 (基の選び方に無関係) Th. (Sylvesterの慣性法則) φ(x, x) = x12 + … + xs2 - xs+12 - … - xr2 ⇒正項と負項の個数は一定 2次曲面1) 球面 x2 + y2 + z2 = r2 (r > 0)→ 中心が原点 O(0, 0, 0) or O (0, 0, 0), 半径 r __(x – a)2 + (y – b)2 + (z – c)2 = r2→ 中心が(a, b, c), 半径 r 2) 楕円面 x2/a2 + y2/b2 + z2/c2 = 1 (a > 0, b > 0, c > 0)放物線/抛物線 (放物線の) parabola Ax. ヘッセの標準形(法線形) Hesse normal form2次元: 直線g: lx + my = nと点P(x1, y1)の距離h ⇒h = |lx1 + my1 - n|/√(l2 + m2) 3次元: 平面p: lx + my + nz = dと点P(x1, y1, z1)との距離h ⇒h = |lx1 + my1 + nz1 - d|/√(l2 + m2 + n2) Pr. v := (x1, y1, z1) → 平行移動
Pは原点にpはq: l(x - x1) + m(y - y1) + n(z - z1) = dに移る = |(-lu - mv - nv)/√(l2 + m2 + n2)| l2 + m2 + n2 = 1 // 3次元(空間)での2直線の位置関係
共有点あり 1点のみ共有点で交わる - 2直線は平面を作る
g1: (x - 2)/2 = (y + 2)/2 = (z - 1)(-1) = s,
g2: x = t + 3, y = 4t + 1, z = t + 5 2s + 2 = t + 3 … (1), 2s - 2 = 4t + 2 … (2), -s + 1 = t + 5 … (3)
(1), (3)からs = -3, t = -1 → (2)を満たさない ⇒ g1, g2は交わらない
= |2·1 + 2·4 + (-1)·1|/(√(22 + 22 + (-1)2)·√(12 + 42 + 12)) A, B: それぞれg1, g2上の点, g1 ⊥ AB かつ g2 ⊥ AB ⇒ AB Q._ g1: (x - 4)/2 = (y - 3)/2 = z/(-1)
g2: (x + 1)/2 = (y - 4)/(-1) = z - 2
A(4 + 3s, 3 + 2s, -s), B(-1 + 2t, 4 - 2t, 2 + t) → 14s - t + 15 = 0, s - 9t + 10 = 0 ∴ s = 1, t = 1 ∴ A(1, 1, 1), B(1, 2, 3) → AB = (0, 1, 2)
最短距離, h = √((1 -1)2 + (2 - 1)2 + (3 - 1)2) = √5 ABの方程式: x = 1, y - 1 = (z - 1)/2 直線と平面直線[I] 点P0(r0)を通り、ベクトルaによって定まる直線の方程式
ベクトル方程式: r = OP → OP = OP0 + P0P, P0P := ta (t ∈ R) r = r1 + t(r2 – r1), or r = (1 – t)r1 + tr2 [III] 同一平面上にない3点 P1(r1), P2(r2), P3(r3)によって決まる平面方程式[IV] 点 P1(r1)から平面(n, r – r0)に下した垂線の長さ 平面Ax. (a, b, c) ≠ (0, 0, 0), d ∈ ℜ ⇒ax + by + cz + d = 0はn = (a, b, c)に垂直な平面の方程式 Pr. A(x0, y0, z0), n = (a, b, c) ⊥ H (平面), P(x, y, z)がH上にあるN.S.C.⇒ AP·n = (x - x0, y - y0, z - z0)·(a, b, c)
= (x - x0)a + (y - y0)b + (z - z0)c
d := - ax0 - by0 + cz0 → ax + by + cz + d = 0 A1. 平面方程式 ax + by + cz + d = 0 に3点を代入 (d ≠ 0)
-b + d = 0, a + b + c + d = 0, 3a + 3b + d = 0 AB = (1, 2, 1), AC = (3, 4, 0), p // AB, p // AC A3. 法線ベクトルnを使う → n ⊥ AB, n ⊥ AC∴ AB•n = a + 2b + c = 0, AC•n = 3a + 4b = 0 ∴ a:b:c = 4:(-3):2 平面と平面のなす角 Z: A1x + B1y + C1z + D1 = 0
Z: A1x + B1y + C1z + D1 = 0Y: A2x + B2y + C2z + D2 = 0 垂直条件 A1A2 + B1B2 + C1C2 = 0, 平行条件 A1/A2 = B1/B2 = C1/C2 Ex. 点(A, B, C)を通り直線(x - x0)/u = (y - y0)/v = (z - z0)/wを含む平面 Q. 点(A, B, C)を通り、平面 Ax + By + Cz + D = 0 に平行な平面 A. 求める平面: A'x + B'y + C'z + D' = 0
→ 平行条件 A'/A = B'/B = C'/C = t 直交変換Def. スカラー三重積, a = (a1, a2, a3), b = (b1, b2, b3), c = (c1, c2, c3)→ a·(b × c) b × c = (b2c3 – b3c2)i + (b3c1 – b1c3)j + (b1c2 – b2c1)k(i, j, k: 単位ベクトル) ∴ a·(b × c) = a1(b2c3 – b3c2) + a2(b3c1 – b1c3) + a3(b1c2 – b2c1)
= a1b2c3 + a2b3c1 + a3b1c2 – a1b3c2 – a2b1c3 – a3b2c1 |
[自然科学史]
| 日本 | |
|---|---|
|
天文・暦法・本草・数学(算法) – 起源: 中国・朝鮮から伝播 5C: 中国の天文・暦の学問輸入 欽明時代: 百済から暦博士来朝 → 数学(学問)始まる 宝・養老時代(8C初, 唐時代): 官吏養成学校: 租税、建築土木、天文や暦計算必要 → 数学科設置
整数加減乗除、平方根・立方根等 = 算木使用 + 掛算九九 Adams W (三浦按針) 1564-1620: 幾何学講じる – 欧州科学(普及せず) 朝鮮の役(1592-1598) → 第二次中国数学輸入 Ex. 「算学啓蒙」、「算法統宗」(明, 程大位著1593)等 既に貿易業者・商人間に十露盤(算盤)が中国から伝来 + 珠算流行始る 1622(元和8): 毛利重能: 「割算書」 = 算術書発行 = 現存最古の数学書1627(寛永4) 吉田光由(1598-1672, 京都)「塵劫記」
数学普及 → 「算法統宗」(珠算書)等を消化し中国数学を日本事情に適応させ書き改める Ex. 日常生活を中心に数々の技術的項目を取り入れ、娯楽性加味し、多数挿絵を入れ、自ら数学を理解させる 天元術(代数)解法: 一つの未知数の代数方程式作成 → 方程式解法研究 → 算木使用算術的な毛利重能の流れを汲む古風な研究法 + 中国天元術(代数)も研究 大坂の橋本正数: 天元術に精通した最初の一人 門人の沢口一之(大坂に住み晩年京都)とで「古今算法記」(1670)を著 保井春海ら: 中国授時暦法学び天体実測結果に適用 - 初の相当な暦に改正 中国から輸入された天元術 = 一元方程式を主とする代数で算木による → 和算家: 天元術記号にヒント - 一種の筆算による代数、点竄(てんざん)作る京都大阪: 橋本正数や沢口一之系統の田中由真、島田尚政らが一種の筆算式の代数を用いていた 江戸: 関孝和と門人が、別記号の筆算代数使用 → 和算(日本固有)が関孝和「発微算法」(1674)から始まる 和算: 徳川時代に発展した日本の数学 関孝和 (1640?-1708): 徳川安定期(西鶴, 芭蕉, Newton, Leibniz同時代) 点竄開発者の一人 → 特殊計算法として行列式論完成 島田尚政(大阪)の研究と共に、発見時期・内容はLeibniz行列式論に優る 方程式論も作り、中国の授時暦作成に用いた補間法を日本に伝え進展 中国整数論学び整頓し系統的整理。幾何分野では正多角形理論開拓
和算家研究題目: 円周率、円弧長、円面積、他曲線で囲まれた面積や曲面で包まれた体積を求める
= 和算が中国数学より進み、独自の道を歩みだした点に大きな貢献 建部賢弘(1664-1739, 関孝和弟子中傑出): 帰納的数学研究法
+ 久留島義太(?-1757) + 松永良弼(?-1744) 和算家は解析学(無限を取り扱う数学)の第一歩に確実に到達 = 無限概念 → 特殊形無限級数 → 関連し「円理」という学問確立 山路主住(1704-1772): 関流制度化 → 皆伝秘儀化
→ 関流開祖関孝和: 人物・業績伝説化 西洋数学の影響天文・暦法
本木良永 1735-1794: 1774 「天地二球用法」 – 地動説 吉宗側近に用いられた建部賢弘や中根元圭(1662-1733)等は、1726年には中国書を通じ間接に西洋数学(算術、書等代数、初等幾何、三角法、対数など17世紀の初めまでのデカルト以前の数学)に接した 1772-1800 (安永-天明、寛政時代): 徳川封建制そのもの矛盾表面化
本居宣長等国学勃興、儒学官私論争、蘭学の本格的進展等
根本精神: 通術(科学的に共通な一般的方法)求め数学を系統的簡単化 |
和算最高頂天文暦術でも麻田剛立の様な先覚者の門から高橋至時や間重冨が出て、革新的な寛政暦(1797)完成→ 伊能忠敬測量事業を指導 蘭学発達し志築忠雄「暦象新書」(1798-1803, 訳述書) → ヨーロッパ物理学(特にニュートン力学)伝わる関連し微小数概念やサイクロイド様曲線等みえる 本多利明(1744-1821): 和算家。蘭学にも関心寄せ名高い経世家・経済学者文化・文政時代 (1804-1829)
和田寧 1787-1840: 安島直円の円理を改良し微小切線を利用する方法案出。多くの表を作り積分計算簡素化に成功(当時の円理で積分函数は代数函数の特殊形に限られ一般性は狭い)しヨーロッパ微積分に近づく
徳川時代でも論理学未発達 → 和算も十分な論理体系持ち得なかった
Ex. 建部賢弘「不休綴術」(1722): 直感的・帰納的に研究する和算家の方法に裏書した方法論書
和算家ギルド = 秘伝主義 + 数学独占 → 大衆数学進歩停滞 開港-明治時代1858: 日本開港 → 国防のため西洋数学正式に学ぶ必要1855: 海軍伝習所 → オランダ人から航海術等と共に西洋数学学ぶ 1862: 陸軍もフランス軍制学ぶ 1863: 幕府開成所 → 西洋数学講義始まり、民間にも「蘭学、洋算及び航海術」塾開かれる 和算から離れた生粋の西洋数学(洋算)を系統的に説いた入門書刊行 Ex. 柳河春三(1832-1870)「洋算用法」(1857): 整数小数四則と比例のみ → 記号や説明は現代的 1868(明治維新): 一切は「日本は如何に、西洋先進諸国に追いくか」に集中国策上 → 数学 = 洋算 → 和算廃止 1872: 日本教育目指し学校制度革新 → 小学校-大学「和算廃止洋算専用」航海術、戦術や自然科学や産業技術 = 西洋書物 = 洋算 当時の洋算本 = 原書の外に中国訳の西洋数学書→ アヘン戦争後、上海に来た英学者が中国人と協力し翻訳 → 維新前から日本輸入 → 現代言葉で、算術, 代数, 幾何, 三角法, 微積分, 函数等 - 皆中国に負う萩原禎助, 1828-1909: 群馬県農村の人で、日本最後の有力和算家
岡本則録(1847-1931): 洋算家(和算から転向)。M10年代数学界指導者 紡績業を尖端とし第一次産業革命 1886 教育行政革新: 進歩的 + 官僚的画一性 → 学校制度統一 → 帝国大学令発布菊地大麓(1855-1917): イギリス留学 + 藤沢利喜太郎(1861-1933): 東京大学物理科出身、ドイツ留学 → 数学指導研究の中心 1894 日清戦争: 封建的和算滅び、近代的・国際的数学を学校教育に導入 → M30: 京都国大学理工科新設1902: 中学校教授要目公布: 中等数学教育統制(小学校はM38頃から国定算術教科書) M37-8: 日露戦争直後から、日本はいっそう急速な発展を遂げた M44: 数学研究を狭く大学内に限らず、広く開放し奨励する方法を講じる一つとして東北帝国大学新設 1991 算数五輪委員会: 広中平祐提唱設立 1992 第一回算数五輪大会 |
| 中国 | |
|
墨子: ユークリッド的論証性 (Cf. 孔子, BC551-BC479, 孟子, BC390-BC305) 漢(BC206-AD220): 官僚的価値観が基調 → 操作的・実用的 Ex. 「九章算術」作者不明 劉徽 (三国魏): 「九章算術」の注釈書祖沖之 429-500: 華北地方名門祖氏一族。南朝宗天文台太史令 「易老荘義釈」、「論語孝経注九章」、数学書に「綴術」 唐(7C-9C): 算学(数学学校) – 下級官僚養成のため教科書「算経十書」: 漢代以来の数学書中から十部を選び寄せ集めた → 数学書散逸が免れる(一部消失) 清: 全書籍を経・史・子・集の四部に分け収集整理するプロジェクト
戴震: 数学部門担当 「十部算経」大半蘇る = 戴震校「算経十書」とし出版 → 代数学(天元術)を中心に活発な動き 秦九韶 (1208-1268, 四川省生): 18歳で義兵挙げモンゴル軍と戦う(逸話?)
モンゴル軍勢力四川省に及ぶ → 逃れ南宋支配地域に行き役人となる |
李治(1192-1279), 河北省石家庄地区生
地方支配していた金の役人 → モンゴル軍侵入 - 失職、放浪生活
←____3 + 1____→
「詳解九章算術」(1261): 「九章算術」解説書 Ex. 12 + 22 + 32 = 3(3 + 1)(2 × 3 + 1)/6 朱世傑, 北京市(現)近郊生: 地方渡り歩いた後、揚州市(現)に住む
市民に数学を教え生活 |