(Upload on April 29 2016) [ 日本語 | English ]
Mount Usu / Sarobetsu post-mined peatland
From left: Crater basin in 1986 and 2006. Cottongrass / Daylily
HOME > Lecture catalog / Research summary > Glossary > Mathematics
|
Gr. μαθημα. Engl. Mathematics
(History of Natural sciences) HistoryThree Greek geometric problems (ギリシア幾何学三大問題)a set of geometric problems whose solution was sought using only compass and straightedge:
Fibonacci (alias), Leonardo da Pisa 1170-1250 "Liber Abaci": introduced Indian-Arabic mathematics, numeration, calculation, etc. Descartes René 1596-1650: founder of analytic geometryTartaglia-Cardano: solution of third degree equation or cubic equation Tartaglia, Niccolò Fontana (1499/1500-1557) and Cardano, Gerolamo (1501-1576) Cardano–Tartaglia formula (= cubic equation): ax3 + bx2 + cx + d = 0 Oresme, Nicole 1323-1382: concept and symbol of power, n on anStifel, Michael 1486-1567: "Arithmetica integra" - concept of logarithm Ferrari, Lodovico 1522-1565: solution of biquadratic equation Gunter, Edmund 1581-1626: trigonometric function, logarithmic table invented Gunter rule (prototype of slide rule) Barrow Isaac 1630-1677: reverse tangent (逆接線) →find out the original curve by detecting the characteristics of tangent = the beginning of infinitesimal calculus Newton: differentiation (called fluxion at that time) and integrationLeibniz, Gottfried Wilhelm 1646-1716, Germany: competition to the priority of differential and integral calculus Bernoulli, Jacques 1654-1705: one of the Bernoulli Family1/12 + 1/22 + 1/32 + … → convergence Bernoulli, Jean 1667-1748: Farther of DanielBernoulli, Daniel 1700-1812, Switzerland (born in Holland) mathematics and physics Euler, Leonhard 1707-1783, math and astronomy
1735 solved Basel problem
Königsberger Brückenproblem
1748 proved Euler's formula eiz = cosz + isinz 
Graph theory (グラフ理論)Def. the study of graphs, which are mathematical structures used to model pairwise relations between objectsDef. Graph: an ordered pair G = (V, E) comprising,
V, a set of vertices (nodes or points, 頂点/節点) Ex. Eulerian trail or path (オイラー路): solution of Königsberg bridges Q. Reaching an island or mainland bank other than via one of the bridges, or accessing any bridge without crossing to its other end Pr. Euler path: a route around a graph that visits every edge once
The number of vertices of odd degree must be either zero or two |
[ calculus ]
quaternion (四元数) icosian game or Hamilton puzzle Def. complete graph (完全グラフ), Kn: a graph in which every pair of distinct vertices is connected by a unique edgeAlembert (d'), Jean Le Rond 1717-1783, France, mathematics, physics and enlightenment: edited Encyclopedie universelle des arts et sciences (百科全書) with Diderot, Denis (1713-1784) Laplace, Pierre Simon, Marquis de 1749-1827, France, mathematics, astronomy and physics (probability, equation and geodesy)left his name Laplace transformation or transform Gauss, Karl Friedrich 1777-1855, Germany: algebra, geometry, analysis
left his name gauss (G) on the electromagnetic unit (EMU), gauss proposed the analytical theory of heat or thermodynamics (contributed the development of mathematical physics) Poisson, Siméon Denis 1781-1840, FranceProbability theory and static electromagnetics Poncelet, Jean Victor 1788-1867, France
Study on geometry when he was in jail because he became captive during joining an army for the conquest to Russia by Napoleon I 1831: complex number (複素数) Lobachevsky NI 1793-1856, Russia / Bolyai J 1802-1860, Hungary
Lobachevskian geometry → hyperbolic geometry Galois E (ガロア) 1811-1832 Research on the bacground of theory proposed by Abel → establishing group theory (群論) Riemann, Georg Friedrich Bolyai 1826-1866, GermanyNon-Euclidean axiom: no pararell lines exist Poincaré, Jules Henri 1854-1912, France: mathematics, physics and philosophy
Cousin of The president Poincaré R (1860-1934)
Prime number theorem (PNT) |
|
Def. Algebraic function (代数関数): a function defined as the root of a polynomial equation
= rational function (有理関数) + irrational function (無理関数) Transcendental function (超越関数)Elementary transcendental function (初等超越関数)function that is not algebraicEx. trigonometric function (f), exponent f, logarithmic f Elementary f = algebraic f + elementary transcendental fExponent function (指数関数)Law. exponential law (指数法則): b > 0, ax > 0 ⇒
axay = ax+y → ax/ay = ax-y Logarithmic function (対数関数)Def. Power function (冪関数)Ex. lim(1 + a/x)x = eaPr. a/x = 1/y → (1 + a/x)x = (1+ 1/y)ay = ((1 + 1/y)y)a continuous
x → +∞, a > 0 → y → +∞, a < 0 → y → –∞ Def. Hyperbolic function (双曲線関数)x ∈ ℜ (-∞ < x < ∞) ⇒coshx = (ex + e-x)/2 (hyperbolic cosine 双曲線余弦) sinhx = (ex - e-x)/2 (hyperbolic sine 双曲線正弦) ⇒ graph: catenary (懸垂線) tanhx = sinhx/coshxcothx = coshx/sinhx sechx = 1/coshx coshx (or cosechx) = 1/sinhx ⇒ inverse hyperbolic function (逆双曲線関数) Prop. (1) cosh2x - sinh2x = 1
(2) tanhx = coshx/sinhx
sinh(x ± y) = sinhxcoshy ± coshxsinhy (4) limtanhx = 1, and limtanhx = -1 Pr._(1) cosh2x - sinh2x = (coshx + sinhx)(coshx - sinhx) = ex·e-x = 1 //
(2) trivial //
= (ex + e-x)/2·(ey + e-y)/2 + (ex - e-x)/2·(ey - e-y)/2
(4) limtanhx = lim((1 - e-2x)/(1 + e-2x)) = 1 Def. Trigonometric function (三角関数)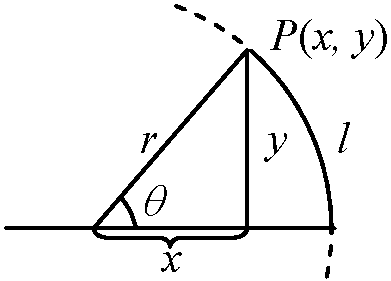 sine (正弦): sinθ = y/r
sine (正弦): sinθ = y/rcosine (余弦): cosθ = x/r tangent (正接): tanθ = x/y = sinθ/cosθ cotangent (余接): cotθ = x/y, = 1/tanθ secant (正割): secθ = r/x, = 1/cosθ cosecant (余割): cosecθ = y/x = 1/sinθ tanθ = sinθ/cosθ, cotθ = cosθ/sinθ Cycle (周期): sinθ, cosθ, secθ, cosecθ → 2π, tanθ, cotθ → π → sin(π/2 – θ) = cosθ, cos(π/2 – θ) = sinθ, sinnπ = 0 limθ→0(sinθ/θ) = 1, |θ| ∠ 1 → sinθ ≈ θ sin(–θ) = –sinθ, cos(–θ) = cosθ, tan(–θ) = –tanθsin2θ + cos2θ = 1, 1 + tan2θ = sec2θ, 1 + cot2θ = cosec2θ Th. lim(sinx/x) = 1 Ex. lim(tanx/x) = lim(sinx/x)·(1/cosx) = 1 Ex. limsin(sinx)/x = lim(sin(sinx)/sinx)·(sinx/x) = 1·1 = 1 (∵ x → 0 ⇒ sinx → 0) |
Equations of trigonometric function
ΔABC, AB = a, BC = b, CA = c, ∠A, ∠B, ∠C ⇒ Th. sine theorem (正弦定理): a/sinA = b/sinB = c/sinC= 2R (R: radius of circumcircle) Th. cosine theorem (余弦定理)
a2 = b2 + c2 + bccosA
sin(x ± y) = sinxcosy ± cosxsiny
sin2x = 2sinxcosx
sin3x =3sinx – 4sin3x
sin2x/2 = (1 – cosx/2)
sinαcosβ = 1/2{sin(α + β) + sin(α – β)}
sinα + sinβ = 2sin((α + β)/2)cos((α – β)/2) Pr. ∀ε > 0, ∃δ > 0, |x – a| < δ → |sinx – sina| < ε
|sinx – sina| = |2sin((x – a)/2)·cos((x + a)/2)| < x – a < δ (= ε) asinθ + bcosθ = √(a2 + b2)·sin(θ + α) Here, α is obtained by: cosα = a/√(a2 + b2), sinα = b/√(a2 + b2) Pr. asinθ + bcosθ = √(a2 + b2)·((a/√(a2 + b2))·sinθ + (b/√(a2 + b2))·cosθ)= √(a2 + b2)·(cosαsinθ + sinαcosθ) = √(a2 + b2)·sin(θ + α) // _____________________from addition theorem Ax. t := tan(x/2) ⇒cosx = (1 - t2)/(1 + t2), sinx = 2t/(1 + t2), dx = 2/(1 + t2)·dt Pr. cos2(x/2) = 1/(1 + tan2(x/2)) = 1/(1 + t2)
From double-angle formula, = 2·1/(1 + t2)·t = 2t/(1 + t2)
t = tan(x/2), differentiate both sides Def. Inverse trigonometric function (逆三角関数)= cyclometric functionsin-1x = arcsinx: x = siny (-1 ≤ x ≤ +1) cos-1x = arccosx: x = cosy (-1 ≤ x ≤ +1) tan-1x = arctanx: x = tany (∀ℜ) cot-1x[-∞, +∞] = arccotx: x = coty (∀ℜ) sec-1x = arcsecx: x = secy (x ≤ -1 or 1 ≤ x) csc-1x = arccscx: x = cscy (x ≤ -1 or 1 ≤ x) Q. Solve (1) sin-1(1/2), (2) tan-1(-√3) and (3) sin-1(sin(3/5·π)) (-π/2 ≤ θ ≤ π/2) A._(1) θ := sin-1(1/2), sinθ = 1/2 ∴ θ = π/6 ∴ sin-1(1/2) = π/6__ (2) θ := tan-1(-√3), tanθ = -√3 ∴ θ = π/3 ∴ tan-1(-√3) = π/3 __ (3) θ := sin-1(sin(3/5·π)), sinθ = sin(3/5·π) ∴ θ = 2/5·π ∴ sin-1(sin(3/5·π)) = θ = 2/5·π |
|
1874 Cantor Georg (1845-1918): established set theory |
Law. Basic formulae (基本公式)Idempotent law (冪等法則) A∪A = A, A∩A = ACommutative law (交換法則) A∪B = B∪A, A∩B = B∩A Distributive law (分配法則)
A∪(B∪C) = (A∪B)∪C Double complement law (復元法則) (AC)C = A De Morgan's law (ド・モルガンの法則)
(A∪B)C = AC∩BC (A∩B)C = AC∪BC |
|
Def. Gauss notation (ガウス記号), [•]: x ⊂ ℜ, a ⊂ Z, a < x
⇒ max(a) ≡ [x] Ex. [-2] = -2, [π] = 3, [1 - √5] = -2Ax. ∀x ⇒ x - 1 < [x] or [x] ≤ x < [x] + 1 Ex. [2 + √5] + [2 - √5] = 4 + (-1) |
Fermat's Last Theorem (フェルマーの最終定理) 1670= Fermat's conjectureTh. No three positive integers a, b and c satisfy the equation an + bn = cn for any integer value of n greater than 2Prior to prove the theory: n = 1: a1 + b1 = c1 ⇒ a + b = c ⇒ infinite solution n = 2: a2 + b2 = c2 (≡ the Pythagorean theorem) ⇒ infinite solution Pr. Case. n = 3 (proven by Euler 1753)
Case. n = 4 (proven by Fermat ≈1630) |
|
Def. Concerned with shape, size, relative position of figures, and the properties of space Def. Euclidean geometry (ユークリッド幾何学): the study of points, lines, shapes, figures and spaces based on the Euclidean five axioms
Plane geometry (平面幾何学) = two-dimensional Euclidean geometry Euclidean geometry ⊃ elementary geometry |
Differential geometry (微分幾何学): using calculus and linear algebra to study problems in geometry Topology (位相幾何学, トポロジー): dealing with the properties of geometry that are unchanged by continuous function Algebraic geometry (代数幾何学): studies geometry through the use of multivariate polynomials and other algebraic techniques Def. circle: the set of all points in a plane equidistant from the center Def. center: fixed point from which all points on the circle are equidistant Def. circumference (円周): the distance around the circle Def. radius, r: the distance from the center to any point on the circle Def. diameter, d: = 2r |
Euclid's five axioms (5公理)
Euclid's five postulates (5公準)
Elementary geometry (初等幾何学)Def. Corresponding angles (同位角): angles in matching positions at two intersections formed by a transversal crossing parallel linesDef. Alternate interior angles (錯角): angles on opposite sides of a transversal and inside the parallel lines. These are also congruent Th. △ABC ⇒ ∠A + ∠B + ∠C = 180° Th. inscribed angle theorem 円周角の定理 half the measure of the central angle that subtends the same arc Trochoid (トロコイド)a roulette formed by a circle rolling along a line (s.l.), including curve and circle
x = aθ - bsinθ
L: a line (the circle center C moves parallel to L) |
Eepitrochoid (外トロコイド)/Hypotrochoid (内トロコイド)a roulette traced by a point attached to a circle of radius r rolling around the outside/inside of a fixed circle of radius R
Cycloid (サイクロイド)= common trochoid
If the cycloid has a cusp (尖点) at the origin and its humps are oriented upward, its parametric equation is: 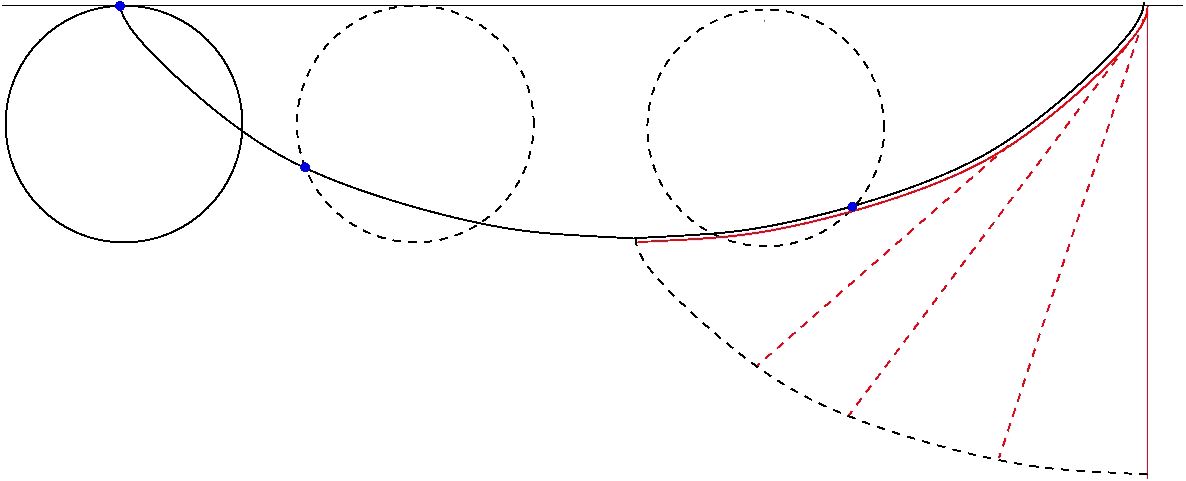 Generation of the involute of the cycloid unwrapping a tense wire placed on half cycloid arc shown in red Astroid (アステロイド, 星芒形) = tetracuspid (四尖点形), cubocycloid, paracycle: a hypocycloid with four cusps If the radius of the fixed circle is a then the equation is given by:
x2/3 + y2/3 = a2/3 ⊂ superellipse
polar coordinates: r = a(1 + cosθ) S = 3/2·πa2, L = 8a Non-Euclidean geometry (非ユークリッド幾何学) Hyperbolic_______Euclidean_______Elliptic |
[ combination and permutation ]
|
a scalar that is computed from the elements of a square matrix and encodes certain properties of the linear transformation described by the matrix (linear albegra)
Expression: det(A), det A, or |A| |
Simultaneous equation (連立方程式)Q. Solve the simultaneous equations (1) and (2)(1) 7x – 4y = 3, -6x + 5y = -1 (2) ax + by + cz = 1, bx + cy + az = 1, cx + ay + bz = 1 A. (1) D2 =
D12 =
D13 = = ab + bc + ca - a2 - b2 - c2 a) a + b + c ≠ 0, a ≠ b ≠ c →
x = D13/D = 1/(a + b + c),
b) a + b + c = 0 → incompatible (不能) |
Two dimensions (二次元)1) Orthogonal coordinates (直交座標)2) Oblique coordinate (斜交座標) 3) Polar coordinate (極座標) Terms: coordinates 座標 axis (pl. axes) 軸 horizontal plane 水平面 horizontal axis 水平軸 hypotenuse 斜辺 normal line 法線 (adj. normal 法線、法線の) orthogonal 直角な parabola 放物線(放物線の) |