(2016年7月7日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 数学 > 微積分学
|
Def. 絶対値 absolute value, |x| < a (a > 0) ⇔ –a < x < a Th. 三角不等式 triangle inequality Def. 式 expression: 数学的対象を表わすために記号を連ねたもの
Def. 項 term ≡ 数・文字の掛算で表す1つの単位 → Def. 次数 degree: 文字を何個かけたかという数
→ degf [ディグリー, デグ]: 多項式fに対しdegfはその次数を表す Def. 多項式の次数: 多項式に含まれる単項式の次数の最大のもの Ex. x3 + 4xy2 + 5z4 + 7 → 次数4 (xの次数3、yの次数2、zの次数4) → 4次多項式 Def. 同次式 homogeneous expression: 多項式中の単項式次数が全て同じ方程式の次数: 方程式の未知数の次数 Ex. 2次方程式 = 未知数の次数が2次 Def. 有理式 rational expression (分数式fractional expression): 2つの多項式の商で与えられる式 |
Ex. 17 – 5 = 1 × 12 → 17 ≡ 5 (mod 12) Def. 斉次一次式 homogeneous linear expression: x1, x2, …, xn →
f(x1, x2, …, xn) = c1x1 + c2x2 + … + cnxn
f(x + y) = f(x) + f(y), f(cx) = cf(x), f(Σi=1ncixi) 部分分数分解 partial fraction decompositionAx. 相加相乗平均 arithmetic-geometric mean |
|
Def. 二項係数 binomial coefficient: 二項展開後した各項の係数
nCk = n!/(k!(n - k)!) n, k: 添字 suffix, k: 無効添字 dummy suffix → 結果に無関係 パスカルの三角形 Pascal's triangle算術三角形論 (1654): 元の数学者朱世傑『四元玉鑑』(1303)に既述二項展開 binomial expansion: (a + b)nを展開すること
0C0 (1)
n = 0___1 Th. 二項定理 binomial theoremニュートンの二項式 (Newton 1644/65) (a + b)n = Σi=0nnCkan – kbk |
Pr0. 統計的証明 (a + b)n = (a + b)(a + b) … (a + b) ________------------ n個 ------------ an-kbkの係数は、n個の因子(a + b)からbをk個選ぶ組み合わせ → nCk // Pr1. 数学的帰納法: 自然数nに対する命題C(n) [10 n = 1 → 成立, 20 n = k → 成立, n = k + 1 → 成立] 10 n = 1 自明 trivial 20 n = kのとき成り立つと仮定 (a + b)k + 1 = (a + b)k·(a + b) = Σi=0kkCiak–ibi·(a + b) = Σi=0kkCiak+1–ibi + Σi=0kkCiak–ibi+1 i + 1 := j → Σi=0kkCiak–ibi+1 = Σj=1k+1kCj-1ak+1-jbj = Σi=1k+1kCi-1ak+1–ibi∴ (a + b)k + 1 = kC0ak+1 + Σi=1k(kCi + kCi-1)ak+1-ibi + kCka0bk+1 = ak+1 + Σi=1kk+1Ciak+1-ibi + a0bk+1 ∴ (a + b)n = Σi=0nnCian–ibi //Def. 一般二項係数, [a:k] (二項係数の拡張): a ∈ ℜ ⇒
[a:0] = 1 |
|
Def. 切断 cut: ℜ (a, 実数) ⊇ A, Aを次の2つの部分集合A1, A2に分ける事
Def. A1 切断の下組, A2 切断の上組 切断条件
Def. 順序数: a ∈ Aset (a: constant), ∀x ∈ A ∀x ≤ a ⇒ a = maxA ≡ 最大値 / ∀x ≥ a ⇒ a = minA ≡ 最小値 Def. 実数, ℜ: a, b ∈ Aset, a ≤ b → a < c < b, ∃c ∈ A → 稠密性をもつ
有理数: density, a < b, a < (a + b)/2 < b
(A1, A2) = not cut. If a ∈ A1 →
a ∈ A1 → a = maxA1, minA2, not exist → |
⇔ Th. Delkindの定理: 切断を与えるとその境界として1つの実数が決まる
Ex for 2: A = (A1, A2) cut →
A1 = {x|x ≤ 0, or x > 0 and x2 < 2, x ∈ A},
0 < ∃h < (2 - a)/3aなるhが存在 Ex. A := 0.3(•) → 10A = 3.3(•) ∴ A = 1/3 → 3A = 0.9(•) = 1 [実数の連続性より矛盾しない] |
|
Def. 数列(実数列) sequence: ある規則に従い並べた数の列 漸化式 recurrence formula: 数列の隣接項の関係式 an + 2 = an + 1 + an (n = 1, 2, …) Ex. フィボナッチ数列 (Fibonacci sequence)素数の数列表現がフィボナッチ数列 Ex. 植物の株の増え方 Def. 部分(数)列 {anp}: 数列{an}の一部分をもとの順序に従って並べたものDef. 特性方程式 characteristic equation: 特性解(k)を求める方程式
an+1 = r·an + d (r ≠ 1) ε-δ論法 (ε-δ definition)limf(x) = l → Def. ∀ε > 0, ∃δ > 0 → |f(x) – l| < ε__[1 > ε 仮定してよい] Ex. lim1/(2x + 3) = 0 Pr. ∀ε > 0, ∃δ > 0, x < δ → 1/(2x + 3) < δを探す
x > 0の時を考えると十分 (∵ x → ∞)
1/(2x + 3) < ε → 1 < ε(2x + 3) → 1 – 3ε < 2εx Def. 極限値 limit value: {an}, ℜ ∋ a, ∀ε > 0, ∃n ≥ n0 ∈ N, |an – a| < ε
⇒ {an}は極限値を持ちaに収束 convergence ≡ liman = a Pr. ε-δ論法 (これ以外証明方法なし)
liman = a, ∀ε > 0, ∃n0(ε) ≤ ∀n, |an – a| < ε [極限の一意性] ≡ ∀nに対し数列anの各項の絶対値がMよりも小さい数列 Th. {an} 収束 ⇒ 有界Pr._limn→∞an := a, ε = 1を選ぶとN = N(1)で n ≥ N ⇒ |an - a| < 1 exist M := max{|a1|, |a2|, |a3|, …, |aN|, |a| + 1} (M, nに無関係な正の定数) 1 ≤ n ≤ N ⇒ |an| ≤ M n ≥ Nならば |an| = |(an - a) + a| ≤ |an - a| + |a| < 1 + |a| ≤ M // 1. 収束数列 (limn→∞an = a) の部分列 {anp} ⇒もとの極限値に収束 limnp→∞anp = a Ex. {an}の部分列{anp} = an1, an2 …, ∀ε > 0, ∨n0 ≤ ∀n →|an – a| < ε → n0 ≤ np, |anp – a| < ε → lim|an| = a Prop. a ∋ ℜ, limn→∞an = aとなるN.S.C. ⇒lima2n-1 = lima2n = a (a = ±∞でも成立) Pr. Case. a ∋ ℜ, ∀ε > 0, N(ε) ∋ ∃N, n ≥ N(ε) ⇒ |an - a| < εN1(ε) ≥ (N(ε) + 1)/2となるよう1つ決める
n ≥ N1(ε) ⇒ 2n - 1 ≥ 2N1(ε) - 1 ≥ N(ε) ⇒ |a2n-1 - a| < ε 同様に n ≥ N1(ε) ⇒ 2n ≥ 2N1(ε) ≥ N(ε) ⇒ |a2n - a| < ε ∴ lima2n = a 成立 If lima2n-1 = lima2n = a → ∀ε > 0, N1(ε) and N2(ε) exist n ≥ N1(ε) ⇒ |a2n-1 - a| < ε, n ≥ N2(ε) ⇒ |a2n - a| < ε
N(ε) := max(N1(ε), N2(ε)), n ≥ N(ε) Ex. {an} = {(-1)n} 偶数項を全てとり{anp}とおくと1に収束 3. 有界数列は必ずしも収束しないEx. (2参照) lim(-1)n ⇒ lima2n = 1, lima2n-1 = -1 (発散) 4. 収束数列で極限値も同じ限界を超えないliman → |an| < ∃M for ∀n → |a| < M Th. {an}, {bn} 収束数列 ⇒ limanbn = liman·limbn ⇔{an}, {bn} 一方が発散する場合は成り立つとは限らない Ex. an = n, bn = 1/n ⇒ limanbn = 1, liman·limbn = ∞·0Th. a ∈ ℜ, {an} (等比数列), liman ⇒ ∞ (a > 1), 1 (a = 1), 0 (-1 < a < 1), 発散 (a ≤ -1) Q. limn→∞{(-1)n/n}の極限A. ∀n ∈ N ⇒ -1/n ≤ (-1)n/n ≤ 1/n, lim(-1/n) = lim(1/n) = 0 ∴ lim{(-1)n/n} = 0 Q. a1 = c, an+1 = 1/2·an + 1の時の{an}の極限A. k = 1/2·k + 1 (特性方程式) ⇒ k = 2, an+1 - 2 = 1/2·(an - 2) [変形]
∴ {an - 2}は初項c - 2、公比1/2の等比数列 ∴ an - 2 = (c - 2)(1/2)n-1 Axiom [I] 実数の連続性 (continuity of real numbers)Ax. 連続の公理 (Dedekind の公理)実数全体にいかなる切断cutを与えてもmaxA1かminA2のいずれか一方しか存在しないDef. 上(下)界: x ∈ A, ∀x < (>) a = constant ⇒
A: 上(下) above(below)に有界 bounded Def. 上(下)限: A ⊂ ℜ ⇒
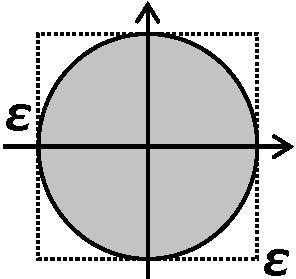
上限(supermum) supA = 最小上界(上界の最小) 
Ex. f(x) < |x2 + y2| = 1
0 ≤ f(x) ≤ 1 → boundedだがf(x) = 1とはならない
∃ε > 0, ∀c ∈ A, a – ε c → a – ε ≥ c ∴ a – ε ≥ c: aの上界 … (1) Th. [II] Weierstraßの定理 (Weierstraß theorem)= 最大値最小値定理(最大値定理), 極値定理 extreme value theorem有界閉集合上の連続関数は最大(小)値を持つ ≡ A ⊂ ℜ (A ≠ ∅), ∃supA (∃infA) ⇒ maxA (minA) exist Pr. ℜ: (B1, B2) cut, B1 = {Aの上界全体}, B2 = {それ以外の実数}
[I]より 1) maxB1 exist, minB2 not exist, or 任意の正の実数a, bに対しb < naとなる自然数n存在 Pr. (背理法) na ≤ bが成立と仮定: A := {na| n ∈ N} → A ⊂ ℜ, A ≠ ∅
A: 上に有界 → Aの上限存在 (Weierstraßの定理より) Pr. If A = {x > 0, xn > a} → A ≠ ∅ (→ (a + 1)n > a), aはAの下界の1つ
→ Aは下に有界 → [II] ∃infA = b (Σr=0n–1nCrbrεn)ε < bn + a – bn = a |
一方infA = b, A ∋ ∀x, b ≤ x, b + ε > x0なる∃x0 ∈ A ≡ a1 ≤ a2 ≤ … an ≤ an+1 ≤ … Def. 狭義単調増加(減少): {an}, ∀n ⇒ an < (>) an+1⇒ Def. 単調数列 monotonic sequence ≡ 単調増加(減少)する数列 Ex. {an} = 2n + 3, {bn} = 1/2n, {cn} = (-5)n, {dn} = 3
{an} = 狭義単調増加, {bn} = 狭義単調減少, {cn} ≠ 単調数列 Th. [III] 上(下)に有界な単調増加(減少)数列はsup(inf)を持つPr. {an}, an ≤ ∃M = constant for ∀n, A = {x: x = an, n = 1, 2 …}
⇒ Aは上に有界 Pr._{an}, an = (1 + 1/n)n, n ≥ 1 (二項定理 →) an = 1 + n·1/n + n·(n -1)/2!·(1/n)2 + … + (n(n - 1)·…·1)/n!·(1/n)n = 1 + 1 + (1 - 1/n)·1/2! + … + (1 - 1/n)·…·(1 - (n - 1)/n)·1/n! < 1 + 1 + (1 - 1/(n + 1))·1/2! + …
+ (1 - 1/(n + 1))·…·(1 - (n - 1)/(n + 1))·1/n!
= (1 + 1/(n + 1))n+1 = an+1 ⇒ {an} 単調増加 ≤ 1 + 1 + 1/2 + 1/22 + … 1/2n-1 < 3 上に有界 ∴ 単調有界数列は収束 ⇒ lim(1 + 1/n)n = a存在 // ⇒ Def. e ≡ a (自然対数の底)Def. e: ネイピア数 Napier's constant / オイラー数 Euler's number e = lim(1 + x)1/x ≈ 2.718281828459045… [無理数] 鮒一鉢二鉢一鉢二鉢至極惜しい Th. lim(1 + 1/x)x = lim(1 - 1/x)-x = lim(1 + x)1/x = eQ. lim(1 + 1/2n)nの極限値 A. m := 2n, n → ∞, m → ∞ ⇒ lim(1 + 1/2n)n = lim(1 + 1/m)1/m = lim{(1 + 1/m)m}1/2 = e1/2 = √e Q. {an}, a1 = 2, an+1 = 1/4·(an2 + 3) (n = 1, 2, 3, …) ⇒ limanを求めるA. liman = 1 収束 Th. {an}, liman = a ⇒ lim{(a1 + a2 + … + an)/n} = a Th. a1 ≤ a2 ≤ a3 ≤ … ≤ … bn ≤ bn-1 ≤ … ≤ b2 ≤ b1 and lim|an – bn| = 0 ⇒ liman = limbn Pr. {an}: 単調増加、上に有界, {bn}: 単調増加、下に有界
[III]からliman = a = supA, limbn = b = infB Th. [IV] Cantorの共通部分定理 (Bachmannの区間縮小法)(1) [a1, b1] ⊇ [a2, b2] ⊇ … ⊇ [an, bn] … かつ (2) lim(an – bn) = 0⇒ [ai, bi] for ∀iの共通点は1点のみ存在 Pr._(1)はTh. IVの仮定を満たす
即ちa1 ≤ a2 ≤ a3 ≤ … ≤ … bn ≤ bn-1 ≤ … ≤ b2 ≤ b1
an ≤ a < a' ≤ bn for ∀n, 0 < a' – a < bn – an → 0 < ∃ε < a' – a → ∴ lim|bn – an| = 0 に対し矛盾 ∴ uniquely determined // 集積点 accumulate point or cluster pointDef. A: 実数(a)の場合, aがAの集積点 ⇔ ∀ε > 0に対し0 < |a – x| < εなるaの近傍中のxがA中に少なくとも1つ(= 無限に多く)存在 a – ε < x < a + ε, (a – ε, a + ε): aの近傍(ε-近傍) neighborhood→ V(a, r), U(a, r) or V(a), U(a) 必要条件: 開 open であることTh. a: Aの集積点 → A ∋ a1, a2, … を選びlimn→∞an = aにすることができる Pr. ε: = 1
0 < |a – a0| < 1なるa0 ∈ A, Th. [V] ワイヤシュトラウス-ボルザノの定理(Weierstraß-Bolzano (W-B) theorem)(ボルザノ-ワイヤシュトラウスの定理, Bolzano-Weierstraß theorem)Th. 点集合Aが有界、無限集合 → Aは少なくとも1つ集積点を持つ ≡ 有界数列は少なくとも1集積値を持つ Pr. A ⊆ [a, b]において[a1, c], [c, b1]
→ 少なくとも一方にはAの元は無限にある → [a2, b2]にはAの元は無限にある
以下同様に[a1, b1] ⊇ [a2, b2] ⊇ [a3, b3] ⊇ … [an, bn] ⊆ (α – ε, α + ε) = U(α): 集積値 // Th. 点集合Aが上(下)に有界ではない→ ±∞を集積点に持つ → 無限集合は少なくとも1つ集積点を持つ Th. Cauchyの収束定理: 数列anが収束するためのN.S.C. (実数の完備性)
数列 an 収束 ⇔ ∀ε, ∀n0 < p, q, |ap – aq| < ε → N.C.
|ap – aq| = |ap – α + α – aq| ≤ |ap – α| + |aq – α| < ε Cauchy列 ⇒ 有界 (∵ Cauchyの収束定理) 極限値不明でもCauchy列となることを示せば収束列である ↔ チェザロ (Cesaro E 1859-1906): 基本列以外にも収束することがある Th. W-Bの定理: 有界な数列は、少なくとも1つの集積点を持つ
→ 集積値がただ1つ ⇒ limn→∞an = a
1/3|α – α'| > p > 0とする ____________________________________↓ Cauchyの収束定理 → W-Bの定理 [V] → Cantorの定理 [IV]_____一般数列 |
|
Def. 方程式 equation: ある特定の値でなければ等号の成立しない式
Def. その値 ≡ 根 root または解 solution Def. 代数方程式 algebraic equation: 未知数の冪powerによる多項式の形で与えられた方程式方程式の代数的解法: 四則演算と冪根power rootのみで解く方法 1次方程式 equation of first degree (linear equation) ax + b = 0, a ≠ 0 → x = –b/a 以下は1次方程式としては考慮しなくてよい
a = 0, b = 0 → 不定 indeterminate: 根は無数 ax2 + bx + c = 0 (a ≠ 0) Case. 因数分解 factorization 可能(x – α)(x – β) = 0 → x = α, β Case. 完全平方式による解の式
x = (–b ± √(b2 – 4ac))/2a
D > 0 実根 real root, s.s.
n次方程式: xn + a1xn-1 + a2xn-2 + … + an-1x + an = 0 ⇒ Case x → a: ∀ε, 0 ≠ |∀x - a| < ∃δ(ε), |f(x) - α| ≤ ε
Def. 極限値 ≡ α__表現: limx→af(x) = α or f(x) → α (x → a)
Def. 極限値 ≡ α__表現: limx→∞f(x) = α or f(x) → α (x → ∞) x → a, f(x), f(y) 収束, limf(x) := α, limg(x) := β ⇒
(1) lim{λf(x) + μg(x)} = λα + μβ__(λ, μ ∈ ℜ) z = g(f(x)) ⇐ y = f(x), z = g(y) Th. 合成関数の極限 U(a), ∃x ≠ a, limf(x) = b, limg(y) = c ⇒limg(f(x)) = c, f(x) ≠ b or g(y) ≠ c at U(a) |
Pr. limg(y) = c → ∀ε > 0, ∃δ > 0
0 < |y – b| < δ → |g(y) – c| < ε → |g(f(x)) – c| < ε … (1) limf(x)が収束するN.S.C.: ∀ε > 0, ∃δ(ε) > 0, 0 < |x - a| < δ(ε), 0 < |y - a| < δ(ε) ⇒ |f(x) - (f(y)| < ε Pr. limf(x) := α, ∀ε > 0, ε* = ε/2 > 0, ∃δ(ε*) > 0 … (1)0 < |x - a| < δ(ε*) ⇒ 0 < |f(x) - a| < ε* if 0 < |x - a| < δ(ε*), 0 < |y - a| < δ(ε*) ⇒ |f(x) - f(y)| ≤ |f(x) - α| + |α - f(y)| ≤ ε* + ε* = ε ⇔ ∀ε > 0, ∃δ(ε) 0 < |x - a| < δ(ε), 0 < |y - a| < δ(ε) ⇒ || < |f(x) - f(y)| < ε {an}, an ≠ a, lim = a, δ(ε) > 0, ∃N(ε) ∈ N ⇒ n ≥ N(ε) ⇒ |an - a| < δ(ε) if m ≥ N(ε), n ≥ N(ε) ⇒ 0 < |am - a| < δ(ε), 0 < |an - a| < δ(ε) (1)より|f(am) - f(an)| < ε__N.C. // 片側極限 one-sided limit= 左極限 left-hand limit + 右極限 right-hand limitDef. 左極限, α: f(x) → (a ∈ ℜ, a + ε0), ∀ε > 0, a < x < a + ∃δ(ε) (> 0)
⇒ |f(x) - α| < ε__(表記) limf(x) = α or f(x) → α (x → a + 0) 収束しなければ発散 ⇒ limf(x) = ±∞ Th. (極限収束N.S.C.) α ∈ N, limf(x) = αとなるN.S.C. ⇒limf(x) = limf(x) = α Pr. limf(x) := α, ∀ε > 0, ∃δ(ε) > 00 ≠ |x - a| < δ(ε) ⇒ |f(x) - α| < ε, a < x < a + δ(ε) ⇒ |f(x) - α| < ε
∴ limf(x) = α 成立
a - δ(ε) < x < a ⇒ |f(x) - α| < ε ∴ limf(x) = α 成立 a < x < a + δ1(ε) ⇒ |f(x) - α| < ε 成立 ∀ε > 0, ∃δ2(ε) > 0 a - δ2(ε) < x < a ⇒ |f(x) - α| < ε 成立 δ(ε) := min{δ1(ε), δ2(ε)} 0 ≠ |x - a| < δ(ε) ⇒ |f(x) - a| < ε ∴ limf(x) = α // |
[ 初等関数 ]
|
Def. ∀ε > 0, ∃δ > 0, |x – a| < δ, U(a, δ)内で全ての点x ⇒
|f(x) – f(a)| < ε → f(x)はx = aで連続 f(a – 0) = f(a) or f(a + 0) = f(a) Th. f(x)が点aで連続となるN.S.C. ⇒ f(x)がaで右連続かつ左連続Def. x ∈ D, f(x) continuous for all x ⇒ f(x): 連続関数 Th. f(x), g(x) continuous ⇒ f(x) ± g(x), f(x)·g(x), f(x)/g(x) (g(x) ≠ 0), |f(x)|, kf(x) (k: constant) 全てcontinuous Pr. trivial. 仮定よりlimf(x) = f(a), limg(x) = g(a) + Th. 関数の極限の性質 //Th. f(x) continuous at x = a, f(a) ≠ 0
1) f(a) > 0 → f(a)f(x) > 0 at U(a) [f(a)とf(x)が同符号である事を証明]
→ |f(x) – f(a)| < |f(a)|/2, δ exist → f(c) = 0, ∃c ∈ (a, b) Pr. f(a) < 0 → f(x) < 0 within U(a), i.e., a ≤ x < ξからf(x) < 0 … (1)
(1)に適合するξの上限supξ = cとおく
一方supξ = c: supξ 最小上界 → c - δ < ξ < cで(1)を満たす → if f(c) < 0 → ∃U(c) st f(x) < 0
(1)からc < ξで(1)を満たす … supξ = cに矛盾__∴ f(c) > 0 f(a) < ∀μ < f(b) or f(a) > ∀μ > f(b) ⇒ f(c) = μ, ∃c ∈ (a, b) Pr._ φ(x) ≡ f(x) – μ … > φ(x), [a, b] continuous,
φ(a) = f(a) – μ < 0, φ(b) = f(b) – μ > 0
欠点: 収束精度は良くない Pr. If f(x), supA not exist → ∃g, f(t) > g, t ∈ [a, b] exist
∴ f(xn) > n, xn ∈ [a, b], {xn} bounded → 集積値 x0 ∈ [a, b] {x'n}: limx'n = x0, limf(x'n) = +∞ → limf(x) = f(x0) = +∞ → 矛盾 // |
i.e., [a, b] continuous → 上に有界 →
M – f(x) ≠ 0 → 1/(M – f(x)): [a, b]でcontinuous → 上に有界 単調増加: f(x1) ≤ f(x2) ⇔ 単調減少: f(x1) ≥ f(x2) Def. 逆関数 inverse function, f-1(x)∀y = f(x) → xがただ1つ定まる (≡ 関数となる) ⇒ x := g(y) → (x, y入替) → y = g(x) ≡ y(x)の逆関数 ≡ f-1(x) Ex. f(x) = x + 1: y = x + 1 → x = y + 1 → y = x - 1 ∴ f(x) = x - 1Ex. f(x) = x2 (x > 0): y = x2 → x = y2 → y = ±√x ∴ 逆関数なし Ex. f(x) = x2 (y > 0): y = √x ∴ f(x) = √x ⇒ 逆関数は常に存在するとは限らない Th. 逆関数の存在: y = f(x) [a, b] continuous,
狭義単調増加: f(a) = α, f(b) = β 一価連続、狭義単調増加
A →into B, A →ontof(a) ⊂ c B f·f-1 = f-1·f = I, f(a) = B → ∃f-1(A) Pr. f(x) 狭義単調増加, α < β(中間値の定理) α < ∀γ < β, f(c) = γとなる∃c ∈ (a, b)が少なくとも1つ存在 If c ≠ c', f(c) = f(c') → 狭義単調増加に矛盾 ∴ cはだだ1つ、即ちf-1(x)は[α, β]で一価に確定 If [α, β] ∋ γ1 ≠ γ2, f–1(γ1) = c1, f–1(γ2) = c2 → f(c1)= γ1, f(c2) = γ2 If c1 > c2 → f(c1) > f(c2) → γ1 > γ2, If c1 = c2 → f(c1) = f(c2) → γ1 = γ2 ∴ γ1 < γ2 → c1 < c2 → f–1: 狭義単調増加 f–1(γ + k) = c + k → f(c + h) = γ + k, f–1(γ) = c →f(c) = γ, f–1(γ + k) – f-1(γ) = h f(c + h) – f(c) = k → limh→0(f(c + h) – f(c)) = 0 →limh→0f(c + h) = f(c) → limh→0(f–1(γ + k) – f–1(γ)) = 0 ∴ limk→0f–1(γ + k) = f–1(γ) → f–1: continuous // |
|
Def. 一価関数: y = f(x) [a, b] Case. x [a, b]の一点cからc + h (h = Δx)まで変化(h ≠ 0) → y: f(c + h) – f(c) = f(c + Δx) – f(c) = Δyだけ変化 ⇒ Def. 平均変化率 Δy/Δx: Δx, Δy ≡ x, yの増分, Δy/Δx = {f(x + h) – f(x)}/hlimΔy/Δx = lim{f(x + h) – f(x)}/h = lim{f(x) – f(c)}/(x – c) exist (有限確定値) Def. 微分係数(微係数, 瞬間変化率), f'(c) ≡ x = cにおけるf(x)y'x = c [プライム, ダッシュ] = df(x)/dx, d/dx·f(x) Def. f(x)の導関数 ≡ y', f'(x), dy/dx, d/dx·f(x), df(x)(f(c + h) – f(c))/h – f'(c) := ρ(h) → f(c + h) – f(c)) = h·ρ(h) + h·f'(c), limρ(h) = 0とも表せる Th. f(x) diff. at a ⇒ f(x) continuous at aPr. if x ≠ a → f(x) = f(a) + (x - a)·{(f(x) - f(a))/(x - a)} limf(x) = lim{f(a) + (x - a)·{(f(x) - f(a))/(x - a)} = f(a) + 0·f'(a) = f(a) // ⇔ 対偶 contrapositive: f(x) discontinuous at a ⇒ f(x) not diff. at a Th. f(x) [a, b] diff. ⇒ f(x) [a, b] continuous (逆は偽)Ex. y = |x| f(x): [a, b] continuous → not differential at x = 0 ∵ lim[f(c + h) – f(c)] = lim[{f(c + h) – f(c)}/h·h] = f'(c)·0 = 0 Def. 接線 ≡ y = f'(a)(x - a) + f(a) (f(x) diff. at a)Def. lim{f(x + h) – f(x)}/h = f'+(c) 右微分係数 ⇒ 収束: 右微分可能 lim{f(x + h) – f(x)}/h = f'–(c) 左微分係数 ⇒ 収束: 左微分可能 Th. f(x)が点cで微分可能(可微分) differentiable (diff.)となるN.S.C.
(1) f(x)が点cで右微分・左微分可能 A. lim(f(h) - f(0))/h = lim(|h|/h)
lim(|h|/h) = lim(h/h) = 1 ∴ 右微分可能 f'+(0) = 1 Th. 合成関数の微分 differentiation of composite function y = f(x) diff. at x = a, z = g(y) diff. at y = b ⇒
z = g(f(x)) diff. at x = a, z' = g'(b)·f'(a) → 微分係数 1) Case: ∃δ → S(δ) not exist 0 < |∃h| < δ → f(a + h) – f(a) = k → k ≠ 0, f(a + h) = b + k (∵ b = f(a))
{f(a + h) – f(a)}/h = a, さらにh → 0 → k → 0 = {g(b + k) – g(b)}/h = {g(b + k) – g(b)}/k·{f(a + h) – f(a)}/h ∴ lim{g(f(a + h) – g(a)}/h = g'(b)·f'(a) 2) Case: ∃δ → S(δ) exist: 証明省略可(大部分の関数は(1)である)対数微分法(logarithmic differentiation) y = f(x) (f(x) ≠ 0) ⇒ log|y| = log|f(x)|とし右辺が微分しやすい時に使う
y = f(x) ⇒ logy = logf(x) (f(x) > 0 ⇒ 絶対値不用)
∴ y'/y = cosxlogx + sinx·(1/x) x = αの近傍 nbd で連続狭義単調変化, diff. at x = α (f'(α) ≠ 0) ⇒
y = f(x)の逆関数 x = y-1(x) = φ(y) diff. at y = β = f(α), φ(β) = 1/f'(α),
f(α + h) – f(α) := k 狭義単調増加からk ≠ 0 → h ≠ 0
= (α + h – α)/(f(a + h) – f(α))
= 1/[(f(α + h) – f(α))/h] |
[ 初等関数 elementary function ]初等関数の微分 differentiation of elementary functionsTh. 対数関数・指数関数の微分 diff. of log and exponential functions
(logax)' = 1/x·logae__Case a = e: (logex)' = 1/x (loga(x + h) – logax)/h = 1/h·loga(1 + h/x) = 1/x·x/h·loga(1 + h/x) = 1/x·loga(1 + h/x)x/h → 1/x·logae (h → 0) Th. 冪関数の微分 f'(x) = (xα)' = αxα–1Pr. y = xα = eαlogx
y' = eαlogx·(αlogx)' = eαlogx·(a/π) (= (a/π)·y)) = αxα-1
logy = αlogx, (1/y)·y' = α/x, y' = α/x·y = α/x·xα = αxα-1 Ex. y = xx ⇒ y': logy = logxx = xlogx ∴ y'/y = x'logx + x(logx)' = logx + 1 ∴ y' = y(logx + 1) = xx(logx + 1) Ex. y = ( )nを微分:
logy =
三角関数 trigonometric function dy/dx = f'(t)/g'(t) = (dy/dt)/(dx/dt) Pr. t = g-1(x) exist, diff. ∴ y = f(t) = f(g-1(x))dy/dx = df/dt(g-1(x))·d/dx(g-1(x)) = f'(t)·1/g'(t) = f'(t)/g'(t) // Q. x = (1 - t2)/(1 + t2), y = 2t/(1 + t2) ⇒ 導関数をtの関数で表せA. dx/dt = -4t/(1 + t2)2, dy/dt = (2 - 2t2)/(1 + t2)2 dy/dx = dy/dt·dx/dt = (t2 - 1)/2t 微分可能性の判定Q. x = 0 diff.を判定。if diff. → f'(0)を求める (1) f(x) = x|x|__ (2) f(x) = xlog|x| (x = ≠ 0), or 0 (x = 0) A._ (1) lim(f(x) - f(0)/(x - 0) = lim(x|x| - 0)/x = lim|x| = 0 ∴ diff. f'(0) = 0(2) lim(f(x) - f(0)/(x - 0) = lim(xlog|x| - 0)/x) = limlog|x| = -∞ ∴ non. diff. Q. f(x) = x2 + 1 (x ≤ 1), or (ax + b)/(x + 1) (x > 1)がx = 1でdiff.となるa, bA. f(x) diff. at x = 1 ⇒ f(x) continuous at x = 1
f(x)はx = 1で左連続、f(1) = 12 + 1 = 2 (f(x) - f(1))/(x - 1) = ((ax + 4 - a)/(x + 1) - 2)/(x - 1) = ((a - 2)(x - 1))/((x + 1)(x - 1)) = (a - 2)/(x + 1)
x = 1, 右微分係数: f'+(1) = (a - 2)/2 = lim((x2 + 1) - 2)/(x - 1) = lim(x + 1) = 2 f'+(1) = f'-(1) ∴ (a - 2)/2 = 2 ⇒ a = 6, b = -2 Eq. y = f(x)の接線 ⇒ f(x) ≈ f'(a)(x - a) + f(a), x = aのnbd (1次近似)陰関数f(x, y): ある区間で一価で幾つかの関数(分枝)に分けられればdiff.
∃y': 両辺をxで微分 f1(x, y) + f2(x, y)·y' = 0 (f2(x, y) ≠ 0) ∴ y' = (x2 – 3y)/(3x – y2) // |
|
f(x) diff. ⇒ f'(x): (第)1次導関数,
f'(x) diff. ⇒ f''(x) = f(2)(x): 2次導関数, …
f(n–1)(x) diff. ⇒ f(n)(x): n次導関数 (n回微分可能) Def. 高次導関数: n ≥ 2の導関数 y(n), f(n)(x), dny/dxnと表すDef. Cn級関数 Cn-class function: I, f(x), n diff., f(n)(x) continuous in I ⇒ Cn級 (C∞級もある) Ex. y = x2 ⇒ y' = 2x, y'' = 2, y(n) = 0 (n ≥ 3) ∴ y = x2 ⊂ C∞級関数Ax. n次導関数公式 equations of n-order derivatives 逐次微分法 successive differentiation: 高次導関数を求める方法: n次微係数: f(n)(x), x = cのときのf(n)(c) Ex. f(x) = xα → f(n)(x) = α(α – 1)(α – 2) … (α – n + 1)xα–nEx. y = 1/(x + 1) → y = (x + 1)-1, y' = (-1)(x + 1)-2, y'' = (-1)(-2)(x + 1)-3, y''' = (-1)(-2)(-3)(x + 1)-4 …, y(n) = (-1)nn!(x + 1)-(n+1) Th. f(x), g(x): n次導関数を持つ⇒ (f(x) ± g(x))(n) = f(n)(x) + g(n)(x) ⇒ (c·f(x))(n) = c·f(n)(x) Law Leibnizの法則 (generalized) Leibniz rulef(x), g(x), n次導関数持つ ⇒ (f(x)·g(x))(n) = Σk=0nnCkf(n–k)(x)·g(k)(x) ≡ 積の微分法を高次導関数に拡張 Pr. (数学的帰納法)n = 1: (f(x)·g(x))' = f'(x)·g(x) + f(x)·g'(x)であるから成立 n = nのとき成立つと仮定しn = n + 1を考える:
(f(x)·g(x))(n+1) = ((f(x)·g(x))(n))' = (Σk=0nnCkf(n–k)(x)·g(k)(x))' ここでk - 1はk index |
= f(n+1)(x)·g(x) + Σk=1n(nCk + nCk–1)f(n–k+1)(x)·g(k)(x) + f(x)·g(n+1)(x) + n+1Cn+1f(0)(x)·g(n+1)(x) = Σk=0n+1n+1Ckf(n–k+1)(x)·g(k)(x) // Ex. f(x) = tan-1(x)のf(n)(0)
f'(x) = 1/(1 + x2) = n+1C0(1 + x2)·f(n+2)(x) + n+1C1(1 + x2)'·f(n+1)(x) + n+1C2(1 + x2)''·f(n)(x) = 0
∴ (1 + x2)f(n+2)(x) + (n + 1)·2x·f(n+1)(x) + [n(n + 1)/2]·2·f(n)(x) = 0 |
|
Th. Rolleの定理: f(x) [a, b] continuous, (a, b) diff., f(a) = f(b)
⇒ f'(c) = 0, ∃c ∈ (a, b) Pr._ i) f(x) ≡ 0 → f'(c) = 0, st. c = (a + b)/2ii) f(x) > 0 (f(d) > 0, ∃x = d), M > f(d) > 0, f(a) = f(b) = 0
→ f(c) = M > 0なる点cはa, bとは異なる iii) f(x) < 0の時は最小値mをとって同様に証明される // Th'. f(a) = f(b) = k ≠ 0, g(x) ≡ f(x) – k, g(x) [a, b] continuous, (a, b) diff.,g(a) = g(b) = 0 ⇒ g'(c) = 0, ∃c ∈ (a, b) Th. 平均値の定理: f(x) [a, b] continuous, (a, b) diff.
⇒ f(b) = f(a) + (b – a)f'(c), ∃c ∈ (a, b)
f(b) = f(a) + (b – a)f'(a + θ(b – a))
g'(c) = 0 = g(b), g'(c) = 0, ∃c ∈ (a, b),
(a, b) g'(x) ≠ g(a), or (f(b) – f(a))/(g(b) – g(a)) = f'(ξ)/g'(ξ), ∃ξ ∈ (a, b)
k = (f(b) – f(a))/(g(b) – g(a)) … (1) G(x) [a, b] continuous, (a, b) ∃G'(x) ≠ 0 ⇒ f(b) = f(a) + f'(a)(b – a) + (f''(a)/2!)·(b – a)2 + …+ (f(n–1)(a)/(n – 1)!)·(b – a)n–1 + Rn Rn = (f(n)(c)/(n – 1)!)·(b – c)n–1·(G(b) – G(a))/G'(c), ∃c ∈ (a, b) Pr. x := a,F(x) = f(b)– {f(x) + f'(x)(b – x) + (f''(x)/2!)·(b – x)2 + … + (f(n–1)(x)/(n – 1)!)·(b – x)n–1} F(x) [a, b] continuous, (a, b) diff. (Cauchyの平均値の定理 ⇒) (F(b) – F(a))/(G(b) – G(a)) = F'(c)/G'(c), ∃c ∈ (a, b)
F(b) = f(b) – f(b) = 0 + (f(n–1)(a)/(n – 1)!)·(b – a)n–1} = Rn d(f(k)(x)/k!·(b – x)k)/dx = f(k+1)(x)/k!·(b – x)k – f(k)(x)/(k – 1)!·(b – x)k–1, k = 1, 2, …, n – 1 |
∴ F'(x) = –f'(x) –Σk=1n–1{f(k+1)(x)/k!·(b –x)k – f(k)(x)/(k – 1)!} = –f(n)(x)/(n – 1)!·(b – x)n–1
∴ (0 – Rn)/(G(b) – G(a)) = (–f(n)(x)/(n – 1)!·(b – x)n–1)/G'(c) ⇒ f(b) = f(a) + {(b – a)/1!}f'(a) + {(b – a)2/2!}f''(a) + … +{(b – a)n - 1/(n – 1)!}f(n-1)(a) + Rn, ∃c ∈ (a, b) Lagrangeの剰余: Rn = (1/n!)f(n)(c)(b – a)n, ∃c ∈ (a, b)Cauchyの剰余: Rn = f(n)(c)/(n – 1)!·(b – c)n–1(b – a), ∃c ∈ (a, b) Pr. φ(x) := (b – x)n, φ(b) = 0, φ(a) = (b – a)n, φ'(c) = -n(b – c)n–1 Lagrange (前定理より) Rn = (f(n)(c)/(n – 1)!)·(b – c)n–1·(0 – (b – a)n)/(-n(b – c)n–1) = f(n)(c)/n!·(b – a)n φ(x) := b – x, φ(b) = 0, φ(a) = b – a, φ'(c) = -1 Cauchy (前定理より)Rn = (f(n)(c)/(n – 1)!)·(b – c)n–1·(0 – b + a)/(-1) = f(n)(c)/(n – 1)!·(b – c)n–1(b – a) // n = 1 ≡ 平均値の定理: (c – a)/(b – a) = θ, 0 < θ < 1 → c = a + (b – a)θ
Lagrange': Rn = (1/n!)f(n)(a + (b – a)θ)(b – a)n
Lagrange'': Rn = f(n)(x + θh)/n!·hn
b = x, + f(n-1)(a) /(n – 1)!·(x – a)n-1 + Rn ⇒ f(x)のx = aを中心とするTaylorの展開式
Lagrange''': Rn = f(n)(a + θ(x – a))/n!·(x – a)n Th. Maclaurinの定理 (Maclaurinの展開) Maclaurin's theorem f(x) = f(0) + f'(0)·x + f''(0)/2!·x2 + … + f(n–1)(0)/(n – 1)!·xn–1 + Rn
Rn = f(n)(θx)/n!·xn, 0 < θ < 1
Rn = f(n)(c)/((n – 1)!p)·(b – c)n–p(b – a)p, c ∈ (a, b)
→ [f(x)をx – aの昇べき順に展開したもの] + f(n-1)(a)/(n – 1)!·(x – a)n-1 + f(n)(a)/n!·(x – a)n |
|
Def. ランダウの記号: lim(h(x)/g(x)) = 0 ⇒ h(x) = o(g(x)) (x → a) Ex. lim(cosx - 1)/x = lim(-sinx/1) = 0 ∴ sinx - x = o(x) Th. 漸近展開 asymptotic expansion: f(x) ∈ I, Cn-class ⇒ f(x) = Σk=0nf(k)(0)/k!·xk + o(xn) (x → 0) Pr. (MacLaurinの定理) x ∈ I, 0 < ∃θ < 1 ⇒ f(x) = Σk=0n-1f(k)(0)/n!·xn
∴ f(x) = Σk=0nf(k)(0)/k!·xk + (f(n)(θx) - f(n)(0))/n!·xn |θx| < |x| → 0 (x → 0)
∴ lim(h(x)/xn) = lim(f(n)(θx) - f(n)(0))/n! = (f(n)(0) - f(n)(0))/n! = 0 関数の変動Def. 増加/減少 f(x): x = c ± h (h > 0) ⇒f(c – h) < f(c) < f(c + h) 増加 ⇔ f(c – h) > f(c) > f(c + h) 減少 Th. 1. f(x), differential at x = c ⇔f'(c) > 0 増加 increase ⇔ f'(c) < 0 減少 decrease_ f'(c) = 0 増減不明 Pr. f(c + h) – f(c) = h{f'(c) + ρ(h)}, h → 0
⇒ ρ(h) → 0, 0 < |h| < δ, ∃δ > 0 ⇒ |ρ(h)| < |f'(c)| ⇒ f(x) ≡ 定数関数 constant function Pr. a < ∀x0 ≤ b, f(x) continuous at [a, x0], diff. in (a, x0)(f(x0) - f(a))/(x0 - a) = f'(c), a < ∃c < x0 (平均値の定理 ⇒) f'(c) = 0 ∴ f(x0) - f(a) = 0 ∴ f(∀x0) = f(a) // Th. 2. f(x): [a, b] continuous, (a, b) differential⇔ [f'(x) ≥ 0 increase, f'(x) ≤ 0 decrease] Pr. (f(x2) – f(x1)/(x2 – x1)) = f'(c), ∃c ∈ (x1, x2)
f'(x) ≥ 0 → f(x2) ≥ f(x1) ∴ increase
f(x), x = c ± h (h > 0) → f(x ± h) < f(c) 極大, f(x ± h) > f(c) 極小 必ずしも逆は成り立たない ex. f(x) = x3 Th. 3. f(x): [a, b] continuous, (a, b) diff., 適当にcをとる.f'(x) > 0 in (a, c), f'(x) < 0 in (c, b) ⇒ f(x) = cで極大 Pr. 狭義単調増加 a < x1 < c → f(x1) < f(c)
狭義単調減少 c < x2 < b → f(c) > f(x2) ⇒ f'(c) = f''(c) = f'''(c) = … = f(n–1)(c) = 0, f(n)(c) ≠ 0 1) n = even: f(n)(c) > 0 → 極大 / f(n)(c) < 0 → 極小2) n = odd: f(n)(c) > 0 → increase / f(n)(c) < 0 → decrease (極値ではない) Pr. n = 1 ⇒ Th.3の拡張 = 自明。n ≥ 2の証明のみ必要 f(c + h) = f(c) + (f'(c)/1!)·h + (f''(c)/2!)·h2 + … + (f(n–2)(c)/(n – 2)!)·hn–2 + Rn-1 仮定 f'(c) = f''(c) = … = f(n-1)(c) = 0から
f(c + h) – f(c) = [hn–1/(n – 1)!]f(n–1)(c + θh) (0 < θ < 1) f(n)(c) > 0 →Th. 1 f(n–1)(c)はx = cで増加の状態 1) h < 0のとき(n: even): f(n–1)(c + h) < 0, c + h < c + θh < c
f(n–1)(c + h) < f(n–1)(c + θh) < f(n–1)(c), f(n–1)(c + h) < 0, f(n–1)(c) = 0
f(c + h) > 0, c < c + θh < c + h, f(n–1)(c) = 0, f(n–1)(c + h) > 0 f(x), D ∋ ∀x, ∃c: f(c) ≥ f(x) → 最大 ⇔ f(c) ≤ f(x) → 最小
最大・最小: local → c0-class, continuous
(f(x) - f(a))/(x - a) ≤ (f(b) - f(x))/(b - x) ⇒ 凸関数(下に凸)
1) f(x) 凸(凹)関数 at ∀I ⇒ cはf(x)の変曲点 Th. f''(x) exist at ∀I, f''(c) = 0 (c ∈ I), f'(c – δ)·f'(c + δ) < 0 ⇒ c 変曲点Th. Hermiteの多項式 Hn(x) ≡ (–1)nex2(dne–x2/dxn)
⇒ n次多項式, n ≥ 2, Hn(x) = 0はn個の互いに異なる実根をもつ
H1 = 2x → x = 0, H2 = 4x2 – 2 → x = ±1/√2 limfn(x) = fn(c1) = fn(c2) = … = fn(cn) = limfn(x) Rolleの定理から fn+1(d1) = fn+1(d2) = …
= fn+1(dn+1), d1 < c1 < d2 < c3 < … < cn > dn+1 |
Th. Newton法 (Newton method) [a, b], f(a) = 0, f'(a) ≥ 0, (a, b) → f''(x) > 0,
{xn}, x1 = b, xn+1 = xn - f(xn)/f'(xn) (n = 1, 2, 3, …) f(x), [a, b] 狭義単調増加, f(a) = 0 → f(x) > 0 (a < x ≤ b) … (2) (数学的帰納法) {an}, a < xn ≤ b for all nを証明
n = 1, x1 = b → a < x1 ≤ b成立 f(a) = f(xk) + f'(xk)(a - xk) + f''(c)/2·(a - xk)2
となるa < c < xk exist 0 = f(xk) + f'(xk){a - xk+1 - f(xk)/f'(xk)} + f''(c)/2·(a - xk)2 = (a - xk+1)f'(xk) + f''(c)/2·(a - xk)2
∴ xk+1f'(xk) = af'(xk) + f''(c)/2·(a - xk)2
xk+1 = a + f''(c)/2f'(xk)·(a - xk)2 > a
∴ a xn ≤ b → n = k + 1で成立 ⇒ ∀Nについてa < xn ≤ bが成立 β := limxn
a < xn ≤ b → a < β ≤ b → f(xn) = f'(xn)(xn - xn+1) 不定形の極限値 limit of indeterminate formsTh. ロピタルの定理 (l'Hôpital's rule): f(x) → 0, g(x) → 0, x → a,lim(f(x)/g(x)) = 0/0 = ∞ – ∞ = 00の場合極限値をとる Case 0/0: f(x), g(x), (a – r, a + r) – {a} diff.
limf(x) = 0, limg(x) = 0, g'(x) ≠ 0,
(a – r, a + r) ⊃ [a – r, a + r], f(x), g(x) [a, a + h] continuous, ⇒ limf(x)/g(x) = A (∵ x:= 1/t → x → ∞ ≡ t → 0) f(x) = f(1/t) = F(t), g(x) = g(1/t) = G(t) → F(t), G(t) (0, 1/R) continuousF'(t) = -1/t2·f'(1/t) = -1/t2·f'(x), G'(t) = -1/t2·g'(x), F'(t)/G'(t) = f'(x)/g'(x) (= f(x)/g(x)) t → 0 ∴ limF'(x)/G'(x) = limf'(x)/g'(x) = limf(x)/g(x) = ATh. Case. ∞/∞: f(x), g(x) (a, a + r) diff.,
limf(x) = ∞, limg(x) = ∞, g(x) ≠ 0, g'(x) ≠ 0,
a < x < x' < a + r, [x, x'] continuous, (x, x') diff., g'(x) ≠ 0 |f'(c)/g'(c) – A| = |(f(x') – f(x))/(g(x') – g(x)) – A| < ε/3
∴ |g(x') – g(x)|ε/3 > |f(x') – f(x) – A(g(x') – g(x))| → g(x)で両辺を割る
≥ |f(x')/g(x) – f(x)/g(x) + A| – |A·g(x')/g(x)| |f(x)/g(x) – A| – |f(x')/g(x)| – |A·g(x')/g(x)|
∴ |1 – g(x')/g(x)|ε/3 + |f(x')/g(x)| + |A·g(x')/g(x)| > |f(x)/g(x) – A| → |f(x)/g(x) – A| < 3ε, |1 – g(x')/g(x)| < 1 // Q. k = constant, logx = kxの実数解の個数A. x > 0, logx/x = k, f(x) := logx/x
f'(x) = ((1/x)·x - logx·1)/x2 = (1 - logx)/x2
_x___(0)__…__e__ …_(∞) 解の個数: k > 1/e … 0. k ≤ 0, k = 1/e … 1. 0 < k < 1/e … 2 Def. 無限小 infinitesimal/無限大 infinite: 変数が0に収束[±∞] ⇒ その変数a = ±∞としても同様 1) lim(u/v) = 0 ⇒ uはvより高位の無限小 [uはvより低位の無限大]2) lim(u/v) = ±∞ ⇒ uはvより低位の無限小 [uはvより高位の無限大] 3) lim(u/v) = k ⇒ uはvと同位の無限小[大] (k = 1 → 同値の無限小[大]) 4) lim(u/vn) = k (k ≠ 0) ⇒ uはvに比してn位の無限小[大] (= 第n位の無限小[大]) Ex. 2つの無限小uとvの差が、u, vいずれよりも高位の無限小⇒ uとvは同値の無限小(逆も真) Pr. u – v := δ, lim(δ/v) = 0, u = v + δ, u/v = 1 + δ/v ∴ lim(u/v) = 1 //Th. Duhamelの定理 x = ∞, αi, βi (i = 1, 2, …, n)は全て正で同値の無限小, lim(α1 + α2 + … + αn) = A (finite) ⇒ lim(β1 + β2 + … + βn) = A |
|
Def. I = [a, b] ⇒
Iの分割: Δ:a = x0 < x1 < x2 < … < xn-1 < xn = b ⇒ δ = {xk} Def'. 積分可能: a exist, ∃ε > 0, δ(ε) > 0 exist, |Δ| < δ(ε)なるIの分割Δ, {ξk} ⇒ |S(f;Δ,{ξk} - α| < ε ⇒ Def. (Riemann)積分: α = ∫abf(x)dxTh. ダルブーの定理 (Darboux's theorem): I = [a, b] f(x) ⇒ |Δ| → 0
SΔ(f), sΔ(f) 収束 ⇒
f(x) bounded, M := supf(x), m := inff(x), Δ = {xk}, m ≤ mk ≤ Mk ≤ M, 0 < xk - xk-1 ≤ |Δ| ∴ 0 ≤ SΔ(f) - SΔ1 (f) ≤ (Mk − mk)(xk − xk−1) ≤ (M − m)|Δ| δ(ε) := ε/(2n(M - m)) > 0, |Δ| < δ(ε), I → Δ分割 ⇒ |
0 ≤ SΔ(f) - SΔ'(f) ≤ n(M - m)|Δ| < n(M - m)δ(ε) = 2/ε Δ0 ∪ Δ' → SΔ'(f) ≤ SΔ0(f) ∴ 0 ≤ SΔ(f) - -∫abf(x)dx = (SΔ(f) - SΔ'(f)) + (SΔ'(f) - SΔ0(f)) + (SΔ0(f) - -∫abf(x)dx) < ε/2 + 0 + ε/2 = ε limsΔ(f) = -∫abf(x)dxについても同様 // Def. 振幅, ω(f, I): I = [a, b], f(x) bounded ⇒ω(f, I) = supf(x) - inff(x) = sup|f(x) - f(y)| ≥ 0 ∴ Δ = {xk} ⇒ ω(f, I): I = supf(x) - inff(x) = Mk - mk∴ Σk=1nω(f, Ik)(xk - xk-1) = Σk=1n(Mk - mk) = SΔ(f) - sΔ(f) 過剰和と不足和の差は振幅で分かる Th. (可積分N.S.C.): I = [a, b], f(x) bounded (1-3は同値) ⇒(1) f(x) integrable on I (2) limSΔ(f) = limsΔ(f), viz. -∫abf(x)dx = -∫abf(x)dx (3) Δ = {xk}, Ik := {xk-1, xk} ⇒ limΣk=1nω(f, Ik)(xk - xk-1) = 0 |
[不定積分基本公式 basic formulae]
|
Def. 原始関数 primitive function, F(x) Def. 不定積分 indefinite integrals, ∫f(x)dx = F(x)
f(x) ⊂ I integrable, a ∈ I, ∃C ⇒
F(x) = ∫axf(t)dt + C (x ∈ I) Th'. f(x) continuous on I, a ∈ I ⇒ d/dx∫axf(t)dt = f(x) (x ∈ I) Th. f(x), g(x) indefinite integrals exist, λ, μ ∈ ℜ ⇒ ∫{λf(x) + μg(x)}dx = λ∫f(x)dx + μ∫g(x)}dx Pr. ∫f(x)dx = ∫axf(t)dt + C1, ∫g(x)dx = ∫axg(t)dt + C2λ∫f(x)dx + μ∫g(x)}dx = λ(∫axf(t)dt + C1) + μ(∫axg(t)dt + C2) = ∫ax{λf(x)dx + μg(x)dx} + (C1 + C2) // Th. f(x) indefinite integrals exist on I ⇒ F(x) continuous functionTh. 置換積分 integration by substitutionF(x) = ∫f(x)dx, x = g(t): diff. w.r.t.t. → ∫f(x)dx = ∫f{g(t)}·g'(t)dtx := g(t) → dx = g'(t)dt求めf(x)のxの代りにg(t)をdxの代りにg'(t)dt代入 Pr. F(x) = F(g(t)) ∴ d(F(g(x))/dt = dF/dx·dx/dt = f(x)·g'(t) = f(g(t))·g'(t) //Cf. ∫f'(x)/f(x)dx = logf(x), ∫f'(x)/n√f(x)n–1dx = n√f(x)はよく使う置換積分 Th. 部分積分 integration by parts(f(x)·g(x))' = f'(x)·g(x) + f(x)·g'(x) ⇒ ∫(f'(x)·g(x) + f(x)·g'(x))dx = f(x)·g(x)∴ ∫f(x)·g'(x)dx = f(x)·g(x) – ∫f'(x)·g(x)dx, g(x) := x ⇒ ∫f(x)dx = x·f(x) – ∫x·f'(x)dx Ex. I = ∫logxdx: f(x) = logx, f'(x) = 1/x→ I = xlogx – ∫x·(1/x)dx = xlogx – ∫1dx = xlogx – x Ex. In = ∫sinnxdx (n 自然数)
[:= ∫sinn–1xsinxdx, f = sinn–1x (f' = (n – 1)sinn–2xcosx), = –cosxsinn–1x + ∫(n – 1)sinn–2x(1 – sin2x)dx
In = –cosxsinn–1x + (n – 1)In–2 – (n – 1)In ___In = ∫tannxdx = 1/(n – 1)·(tann–1x – In–2) 有理関数の積分 integration of rational functionsi) ∫A/(x – a)dx = A·log|x – a| + Cii) ∫A/(x – a)kdx = -A/[(k – 1)/(x – a)k-1] + C (k ≠ 1) iii) ∫(Lx + M)/(x2 + q2)kdx = L∫x/(x2 + q2)kdt(1)=Ik + M∫1/(x2 + q2)kdx(2)=Jk A. (1) x2 + q2 := t, dt/2 = xdx, Ik = 1/2∫t–kdt ∴ I1 = 1/2·log|x2 + q2|, I2 = –1/2·(x2 + q2), Ik = –1/2·[(k – 1)(x2 + q2)k–1] (k = 1, 2, 3 …) __(2) f' = 1, g = 1/(x2 + q2)として部分積分Jk = x·{1/(x2 + q2)k} + 2k∫(x2/(x2 + q2)k+1)dt
= x/(x2 + q2)k + 2k∫[{(x2 + q2) – q2}/(x2 + q2)k+1]dt ∴ Jk+1 = 1/q2[x/{2k(x2 + q2)k} + {(2k – 1)/2k}Jk] → k + 1 := k, k = k – 1 Jk = 1/q2[x/{2(k – 1)(x2 + q2)k–1} + {(2k – 3)/2(k – 1)}Jk] [漸化式] iv) ∫(Lx + M)/[(x – p)2 + q2]kdx= L∫x/[(x – p)2 + q2]kdx(1)=In + M∫1/[(x – p)2 + q2]kdx(2)=Jn A.__(1) x – p = t, dx = dt, In = L∫(t + p)/(t2 + q2)kdt → reduce (iii)
(2) (iii-2)とどちらを用いてもよい = 1/q2k–1∫1/sec2k–2θdθ = 1/q2k–1∫cos2k–2θdθ [漸化式] Ex. ∫(x3/(x + 1))dx = ∫(x2 - x + 1 - 1/(x + 1))dx = x3/3 - x2/2 + x - log|x + 1|Ex. ∫(1/(x2 + 4x + 7))dx = ∫1/((x + 2)2 + 3)dx = (1/√3)·tan-1((x + 2)/√3) Th. f(x) = a0 + a1x + a2x2 + … + amxm = Σi=0maixi (1, 2, …, m: integer)
f(x) = 0の1つの実根 a → f(x) = (x – a)r·F(x) (F(a) ≠ 0)なる∃r
∵ f(p + qi) = u(p, q) + iv(p, q) = 0 → u(p, q) = 0, v(p, q) = 0 = [(x – p)2 + q2]kΦ(x) 以上の事から[(x – p)2 + q2]s, (p – a)r, amの形で表わせる // |
実根の場合の積分 f(x) = a0 + a1x + … + amxm = (x – a)r·F(x), F(x) ≠ 0. g(x) = b0 + b1x + … + bmxm
A1 := g(x) – A1F(a) = 0, g(x) – A1F(x) = (x – a)·g1(x) = A1/(x – a)r + A2/(x – a)r–1 + … + Ar/(x – a) + g1(x)/F(x) 無理関数の積分 integration of irrational function (虚根の積分)(1) I = ∫R(x, n√(ax + b))dx
n√(ax + b) := t → ax + b = tn, x = (tn – b)/a, dx = (n/a)·tn–1dt
n√{(ax + b)/(cx + e)} ≡ t, l√(ax + b) = tとして(1)'に還元reduceしp, qのL.C.M.をとるとn/p ≡ ∃p, n/q ≡ ∃q (2) I = ∫R(x, √(ax2 + bx + c)dx
A) a = 0 → reduce to (1) これをIに代入するとIは有理関数の積分となる
C) a < 0 → ax2 + bx + c < 0 (√(ax2 + bx + c)は虚数) not exist
ii) D = 0 → x ≠ -b/2a, ax2 + bx + c < 0 not exist → √(ax2 + bx + c) = √a(x – α)(x – β) := t(x – α)
t2 = a(x – α)/(x – β), ∴ I = ∫R((αt2 – aβ)/(t2 – a), t)(t2 – α)/{2a(β – α)t}dt → reduce (1) (3) I = ∫xm(axn + b)q/pdx (a ≠ 0, b ≠ 0. a, b, p, q: integer)
(axn + b)1/p := t, axn + b = tp = (p/an)∫{(tp – b)/a}(m+1)/n–1tq+p–1dt p + q – 1 integer ∴ (m + 1)/n: integer → integrable Ex. I = ∫x13(1 + x7)3/5dxA. (m + 1)/n = (13 + 1)/1 = 14: integer, x7 = t, x = t1/7, dx = 1/7t–6/7dt I = ∫t13/7·(1 + t)3/5·(1/7t–6/7)dt = 1/7∫t·(1 + t)3/5dt
= 1/7∫(t + 1)8/5dt – 1/7∫(t + 1)3/5dt ∫sinm–1x(sinx·cosnx)dx,
f = sinm–1x, Im, n = sinm–1x{–1/(n + 1)cosn+1x} –∫(m – 1)sinm–2xcosx{–1/(n + 1)cosn+1x}dx = –1/(n + 1)[sinm–1xcosn+1x – (m – 1)∫sinm–2xcosn+2xdx] → cosn+2x = cosnx(1 – sin2x) = 1/(n + 1){–sinm–1xcosn+1x + (m – 1) ∫(sinm–2xcosnx – sinmxcosnx)dx} = 1/(n + 1){–sinm–1xcosn+1x + (m – 1)(Im–2, n – Im, n)} Im, n + (m – 1)/(n + 1)Im, n = 1/(n + 1){–sinm–1xcosn+1x + (m – 1)Im–2, n} ∴ Im, n = 1/(m + n){–sinm–1xcosn+1x + (m – 1)Im–2, n}
以下の簡約公式は同じ |
|
Th. Heine-Borelの被覆定理 f(x) [a, b] continuous, ε1 = ∃ε/2 > 0 (fixed), [a, b] ∋ ∀x1, x2, 0 < |x – x'| < δ'x, |f(x) – f(x')| < ε1, 1/2δ'x = δx ⇒ (x1 – δx1, x1 + δx1)∪(x2 – δx2, x2 + δx2)∪ …∪(xn –δxn, xn + δxn) ⊃ [a, b] → 近傍δxiの和は[a, b]を被覆する Pr. (背理法) [a, b] ∉ (x1 – δx1, x1 + δx1)∪(x2 – δx2, x2 + δx2)∪ …∪(xn –δxn, xn + δxn)を仮定し矛盾を説明 I1 := [a, b] ∉ [a, (a + b)/2], [(a + b)/2, b],I1を覆わない部分がある方をI2 = [a1, b1] nが十分に大きい(n → ∞) In = [an–1, bn–1], |In| = (b – a)/2n–1, a ≤ a1 ≤ a2 ≤ … ≤ < b, b ≥ b1 ≥ b2 ≥ … > a ∴ limn→∞an = limn→∞bn = c ∈ [a, b]∴ In = [an–1, bn–1] ⊂ (c – δc, c + δc) … 仮定と矛盾 // Def. 一様連続 uniformly continuous ∀ε > 0, ∃δ > 0, [a, b] ∋ ∀x1, x2, |x1 < x2| ⇒ |f(x1) – f(x2)| < ε ≡ 一様連続 Pr. Heine-Borel定理においてminΣi=1nδ = δ, |x – x'| < δ → |f(x) – f(x')| < ε
x ∈ (xi – δxi, xi + δxi), |x – xi| < δxi, |x – x'| < δ ≤ δi Pr. (背理法) f(x) = 1/xがI = (0, ∞)で一様連続と仮定 ε = 1, ∃δ = δ(1) > 0 x, y ∈ I, |x - y| < δ ⇒ |1/x - 1/y| < 1 n ∈ N, x := 1/n, y = 1/n + δ/2, |x - y| = δ/2 < δ |1/x - 1/y| = |n - 2n/(2 + δn)| = δn2/(2 + δn) < 1 ⇔ limn→∞(δn2/(2 + δn)) = ∞ (矛盾) // Th. f(x), g(x)はI上で一様連続 ⇒ λ, μ ∈ ℜ, λf(x) + μg(x)もI上で一様連続Pr._ Case. λ = μ = 0: trivial Case (λ, μ) ≠ (0, 0): ∀ε > 0, ε' = ε/(λ + μ) > 0, ∃δ1(ε'), ∃δ2(ε') > 0
x, y ∈ I, |x - y| < δ1(ε') ⇒ |f(x) - f(y)| < ε' δ(ε) := min{δ1(ε'), δ2(ε')}, |x - y| < δ(ε), ∀x, ∀y ∈ I |λf(x) + μg(x) - (λf(y) + μg(y))| ≤ |λ||f(x) - f(y)| + |μ||g(x) - g(y)| < (|λ| + |μ|)ε' = ε // Th. 最大・最小値の定理 f(x) [a, b] continuous⇒ maxf(x) = M, minf(x) = m, m ≤ f(x) ≤ M Pr.___┌──┬──┬──┬──┬──┬──┬──┐ Δ分割
a[x0__x1 ………………… xn-2 xn-1_xn], b[xi, xi+1] = Σi=0n–1f(xi)(xi+1 – xi) = Σi=0n–1f(xi)δi
_________δi 1) Δ'分割: Δ分割に新しい分点を付け加える miδi = miδi1 + miδi2 ≤ mi1δi1 + mi2δi2 (Mi ≥ mi) ≤ Miδi1 + Miδi2 ≤ Mi1δi1 + Mi2δi2 = Miδi ∴ miδi ≤ Miδi 2) 任意の2つの分割Δ、Δ'を考えこれらの分点を分点とする分割Δ''を考える(1)からSΔ'' ≤ SΔ', sΔ ≤ sΔ'' → sΔ ≤ sΔ'' ≤ SΔ'' ≤ SΔ' 3) 有限個の分点を持つあらゆる分割を考える→ SΔ, sΔ supsΔ = s, infSΔ = S, sΔ ≤ SΔ' → sΔ ≤ S → s ≤ S // 3)で特にsΔ ≤ sΔ'' ≤ SΔ'' ≤ SΔ, s = S⇒ ∫abf(x)dx, f(x) [a, b] (定)積分可能 integrable (a: 下端, b: 上端) Th. f(x) [a, b] continuous ⇒ 一様連続cf. f(x) = 1/x (0 < x ≤ 1) continuousだが一様連続でない事もある Pr. (背理法) f(x)はI = [a, b]上で一様連続ではないと仮定し解くAx. I = (a, b], f(x) 連続, 右極限 limf(x)収束 ⇒ f(x) 一様連続 Ax. I = [a, ∞), f(x) 連続, 極限 limf(x)収束 ⇒ f(x) 一様連続 Th. f(x) 単調 (monotone) on I ⇒ f(x) integrable Th. f(x) continuous on I = [a, b] ⇒ f(x) integrable (SΔ = sΔを証明) (cf. [a, b] 不連続 → ルベック積分) Pr. Δを分割し各部分区間もみなδよりも小さくなるようにするとsΔ ≤ supsΔ = s, S = infSΔ ≤ SΔ → S – s ≤ SΔ – sΔ = limn→∞(SΔ – sΔ) = (b – a)·ε // Th. f(x), g(x) continuous on I = [a, b], f(x) ≥ g(x) (a ≤ x ≤ b),f(ξ) > g(ξ), ξ ∈ I exist ⇒ ∫abf(x)dx > ∫abg(x)dx Pr. h(x) := f(x) - g(x) → h(x) continuous on Iδ > 0 exist, C (constant) > 0 exist → |x - ξ| < δ ⇒ h(x) > C
∫abh(x)dx ≥ ∫ξ-δξ+δh(x)dx ≥
∫ξ-δξ+δCdx ≥ 2Cδ > 0 1/(b -a)∫abf(x)dx = f(ξ) Pr. Max = f(x1), min = f(x2) exist → m ≤ f(x) ≤ M (a ≤ x ≤ b)
∫abmdx < ∫abf(x)dx < ∫abMdx ∴ m < 1/(b -a)∫abf(x)dx < M Th. (商) f(x), integrable on I, f(x) ≠ 0, 1/f(x) bounded ⇒ 1/f(x) integrable |
定積分の求め方1) 区分求積(分)法 quadrature by parts: あらゆる分割の極限を整頓limSΔ計算 ⇒ 直接∫abf(x)dx求める 2) 不定積分との関連Th. 区分求積法: f(x), [a, b] 積分可能 ⇒ ∫abf(x)dx = lim((b - a)/n)Σk=1nf(a + (b - a)/n·k) = lim((b - a)/n)Σk=0n-1f(a + (b - a)/n·k) ⇒ a = 0, b = 1 → ∫01f(x)dx = lim(1/n)Σk=1nf[k:n] = lim(1/n)Σk=0n-1f[k:n]Th. 定積分の性質 (f(x), g(x) [a, b] continuous) 1) (線形性) ∫abλf(x)dx = λ∫abf(x)dx (λ: 定数) 1') ∫ab{λf(x) + μg(x)}dx = λ∫abf(x)dx + μ∫abg(x)dx 2) a, b, cの大小がどうであっても∫abf(x)dx = ∫acf(x)dx + ∫cbf(x)dx 3) (単調性) f(x) ≥ 0, a < b ⇒
∫abf(x)dx ≥ 0, 更にf(x) ≥ g(x) → ∫abf(x)dx ≥ ∫abg(x)dx
S(f;Δ,{ξk}) = Σk=1nf(ξk)(xk - xk-1) ≤ Σk=1ng(ξk)(xk - xk-1) = S(g;Δ,{ξk}) Pr. –|f(x)| ≤ f(x) ≤ |f(x)|, a < b → –∫ab|f(x)|dx ≤ ∫abf(x)dx ≤ ∫ab|f(x)|dx // 5) 積分の第一平均値の定理 ∫abf(x)dx = (b – a)f(c), a < c < b Pr. [a, b], maxf(x) = G, minf(x) = g → g(b – a) ≤ ∫abf(x)dx ≤ G(b – a) ∴ g ≤ ∫abf(x)dx/(b – a) = f(c) ≤ G, a < c < b (中間値の定理) // Th. 微積分学の基本定理 f(x) [a, b] continuous, F(x) = ∫axf(x)dx, a < x < b
→ dF(x)/dx = f(x) 閉区間であれば必ず原始関数存在
(一様連続なものがintegrableであることの証明) → G(ai) – G(ai–1) = G'(xi–1)(ai – ai–1) = f(xi–1)(ai – ai–1) ∴ G(b) – G(a) = Σi=0n–1f(xi–1)(ai – ai–1), δ(Δ) → 0 → Σi=0n–1f(xi–1)(ai – ai–1) = ∫abf(x)dx // 置換積分 integration by substitution
f(x) [a, b] continuous, x = g(u) [a, b] (強意の)単調増加(減少), = [f(x)g(x)]ab – ∫abf(x)g'(x)dx, f(x) = x ⇒ [xg(x)]ab – ∫abxg'(x)dx Th1. ∫abf(x)dx = ∫baf(a + b – x)dx = [F(a + b – x)]ba = F(b) – F(a)Th2. ∫0af(x)dx = ∫0a/2(f(x) + f(a – x))dx Ex. ∫0πsinnxdx = ∫0π/2(sinnx +sinn(π – x))dx = 2∫0π/2sinnxdx Th3. ∫-aaf(x)dx = ∫0a(f(x) – f(–x))dxEx. ∫-π/2π/2cosnxdx = ∫0π/2(cosnx – cosn(–x))dx = 2∫0π/2cosnxdx Th4. ∫abf(cx)dx = 1/c∫cacbf(x)dxTh5. f(a – x) = f(x) ⇒ ∫0af(x)dx = 2∫0a/2f(x)dx, f(a – x) = –f(x) ⇒ ∫0af(x)dx = 0 Th6. f(x) 偶関数 even f. f(-x) = f(x) ⇒ ∫-aaf(x)dx = 2∫0af(x)dx,__f(x) 奇関数 odd f. f(-x) = –f(x) ⇒ ∫-aaf(x)dx = 0 Pr. Case. f(x) continuous
∫-aaf(x)dx = ∫0af(x)dx + ∫-a0f(x)dx ∫0af(t)dt even f., -∫0af(t)dt odd f. ∴ when f(x) is odd f., ∫-aaf(x)dx = ∫0af(x)dx + ∫-a0f(x)dx = ∫0af(x)dx + ∫0af(x)dx = 2∫0af(x)dx ∴ when f(x) is even f., ∫-aaf(x)dx = ∫0af(x)dx + ∫-a0f(x)dx = ∫0af(x)dx - ∫0af(x)dx = 0 // Ex. Schwarzの不等式 {∫abf(x)g(x)dx}2 ≤ ∫abf(x)2dx·∫abg(x)2dxPr. f(x) = 0 for ∀x, or a = b → 両辺とも0。よって成立
f(x) ≠ 0なるxが存在と仮定 → ∫abf(x)2dx > 0, |
|
f(x) [a, b] continuous, (a, b) discontinuous
Def. b: 特異点 singular point (不連続点 discontinuous point) Def. 可積分 ∫abf(x)dx = lim∫ab-εf(x)dx 1) 独立について f(x) [a, b] continuous → integrable → ∫abf(x)dx = exist 2) f(x) [a, b] continuous → |f(x)| continuous → integrable. i.e., ∫ab|f(x)|dx = exist 3) f(x) [a, b) continuous, x = bでdiscontinuous (定義する必要なし)
→ lim∫ab-εf(x)dx 有限確定値として存在 := ∫abf(x)dx → lim∫a-εbf(x)dx 有限確定値として存在 := ∫abf(x)dx f(x) [a, b] ∋ c continuous → lim∫ac-εf(x)dx + lim∫c+εbf(x)dx = ∫abf(x)dx 4) 無限積分 infinite integral: 積分範囲が∞を含む積分
f(x) [a, +∞) continuous → ∫a∞f(x)dx = lim∫abf(x)dx, (但し逆は真 Ex. ∫|f(x)|dx exist ⇒ ∫f(x)dx exist) Ax. α ∈ ℜ, constant ⇒
(1) ∫1∞(1/xα)dx 収束 N.S.C. ⇒ α > 1 α ≠ 1 → ∫1∞(1/xα)dx = lim∫1t(1/xα)dx = lim[(x1-α/(1 - α)]1t = lim((t1-α - 1)/(1 - α)) ∴ {-1/(1 - α) (1 - α < 0), ∞ (1 - α > 0)} ⇒ α > 1の時に収束 ______∫01(1/xα)dx = lim∫t1(1/xα)dx = lim[(x1-α/(1 - α)]t1 = lim((1 - t1-α)/(1 - α)) ∴ {∞ (1 - α < 0), 1/(1 - α) (1 - α > 0)} ⇒ α < 1の時に収束 // Th. 特異積分の絶対収束 (比較判定法)f(x), g(x), (a, b], integrable, |f(x)| ≤ g(x) (a < x ≤ b) ⇒
∫abg(x) convergence ⇒ ∫abf(x) convergence limG(t) convergence, ∀ε > 0, ∃δ > 0 a < t1 < a + δ, a < t2 < a + δ ⇒ |G(t1) - G(t2)| < ε
∃t1, ∃t2 ∈ (a, a + δ), t1 ≤ t2 → = G(t1) - G(t2) < ε
t2 ≤ t1も同様 ⇒ a < t1 < a + δ, a < t2 < a + δ ⇒ |F(t1) - F(t2)| < ε ⇒ ∫cbf(x)dx exist___Ex. ∫abf(x)dx = ∞ → ∫cbf(x)dx = ∞ 6) 可積分の十分条件Th. 1. f(x) [c, b] continuous (b singular point), 0 < ∃α < 1, lim(b – x)αf(x) exist ⇒ ∫cbf(x)dx integrable |
Pr. lim∫abf(x)dx integrable in U(b) = (b – ε, b)を示す
|f(x)| < ∃M/(b – x)α, M constant
= M[-1/(1 – α)·(b – x)1–α]ab–ε = M/(1 – α){(b – a)1–α –ε1–α} ε → 0 → |f(x)| > 0 → 積分区間増大 → 単調増加 → lim∫cb+εf(x)dx exist, (5) → ∫cbf(x)dx integrable Th. 2. f(x) [a, ∞) continuous, ∃α < 1, limxαf(x) exist⇒ ∫a∞f(x)dx integrable (1の拡張) Pr. 十分大きいxに対しxα|f(x)| < ∃M = constant, |f(x)| < ∃M/xα∫ax|f(x)|dx < M∫ax1/xαdx = M[1/(1 –α)x1–α]ax = M/(α – 1)·(a1–α – x1–α), α > 1
→ 上に有界, x → +∞ → 単調増加 → +∞ / [a, ∞), x > b, f(x) ≥ M/x → ∫a∞f(x)dx → ∞ [ ガンマ分布 ] Def. オイラーのガンマ関数 Euler's Γ-function, Γ(s)= ∫0∞e-xxs–1dx (s > 0) Ax. Γ関数 ⇒ 収束Pr. (積分区間を分けて考える) i) 0 < s < 1, x = 0はf(x) = e-xxs-1の特異点 → x1-sf(x) = e-x < 1 (0 < x < ∞) ⇒ 収束
ii) x → ∞, e-xxs+1 → 0 ⇒ x2f(x) = e-xxs+1は(1, ∞)で有界 ⇒ 収束 = ∫01xp–1(1 – x)q–1dx (p, q > 0) (p, q ≥ 1 → ordinary) Ax. (p > 0 or q > 0) ⇒ 収束(存在), それ以外のp, qで発散Pr. B(p ,q) = J1=(0, 1/2] + J2=[1/2, 1)
J1 = ∫01/2xp-1(1 - x)q-1dx, J2 = ∫1/21xp-1(1 - x)q-1dx 1 - q < 1 ⇒ ∫01/2xp-1dx = ∫01/2(1/(x1-p)dx ⇒ J1は収束 [1/2, 1) ⇒ xp-1は1と(1/2)p-1 ⇒ 有界 1 - q < 1 ⇒ ∫1/21(1 - x)q-1dx ⇒ J2は収束 // Ax. B(p, q) = 2∫0π/2sin2p-1θcos2q-1θdθ (p > 0, q > 0)Pr. x := sin2θ Ex. ∫0π/2sin5θcos3θdθ = 1/2·B(3, 2) = 1/2·(Γ(3)Γ(2))/Γ(5) = 1/2·(2!1!)/4! = 1/24 Euler functionsの特性Th. Γ(s + 1) = sΓ(s) Pr. Γ(s + 1) = ∫0∞e-xxsdx = [e-xxs]0∞ + s∫0∞e-xxs-1dx = s∫0∞e-xxs-1dx = sΓ(s) // Th. Γ(n) = (n - 1)! or Γ(n + 1) = n! (n: 正整数)Pr. Γ(n) = (n – 1)Γ(n – 1) = (n – 1)(n – 2) … Γ(1) ここでΓ(1) = 1 ∴ Γ(n) = (n – 1)! // Th. (Γ関数-β関数関係) B(p, q) = (Γ(p)Γ(q))/Γ(p + q) (p, q 正整数)Pr. 累次積分からニ重積分への変換と極座標を用いて証明 Γ(p)Γ(q) = 4∫0∞e-x2x2p-1e-x2dx∫0∞e-y2y2q-1dy = ∫0∞2e-r2r2(p+q)-1dr∫0π/22cos2p-1θsin2q-1θdθ = Γ(p + q)B(p, q) // Th. Γ(1/2) = 2∫0∞e-x2dx = √πPr. B(1/2, 1/2) = (Γ(1/2))2/Γ(1), B(1/2, 1/2) = 2∫0π/2dθ = π
ここでΓ(1) = 1 ⇒ (Γ(1/2))2 = π ∴ Γ(1/2) = 2∫0∞e-y2dy = 2∫0∞e-x2dx // |
面積 (area), STh. (極方程式の面積) 曲線 C, r = f(θ) continuous, (α ≤ θ ≤ β)
C, θ = α, θ = βで囲まれる部分の面積 S ⇒
r = f(θ), θk-1, θkが囲む扇形で近似した面積 1/2·f(θk)2(θk - θk-1) ⇒ 1/2∫αβf(θ)2dθ // 長さ (length), lDef. 曲線の長さ: 曲線 C (端点 A, B), 分点 P
→ P0 = A, P1, P2, … Pn-1, Pn = B Ck ≈ Pk-1Pk → Σk=1nPk-1Pk = P0P1 + P1P2 + … + Pn-1Pn maxPk-1Pk → 0 ⇒ Pk-1Pk = L (converge) ≡ 求長可能 ⇒ L ≡ 長さ |
Q. a > 0, C, x = a(t - sint), y = a(1 - cost) (0 ≥ t ≥ 2π
(1) Cとx-axisが囲む部分の面積(S)、(2) Cの長さ(L)を求めよ A. C ⊂ サイクロイド cycloid
(1) S = ∫02πaydx = ∫02π(a(1 - cost)·a(1 - cost))dt = 3πa2 体積・側面積 (volume and lateral area), V and SlTh. [a, b], f(x) ≥ 0 continuous → y(x), x = a, y = bが囲む図形x軸で回る回転体の体積 ⇒ V = π∫ab{f(x)}2dx Th. [a, b], f(x) ≥ 0 C1-class → y(x), x = a, y = bが囲む図形x軸で回る回転体の側面積 ⇒ S = 2π∫abf(x)√(1 + {f'(x)}2)dx Eq. ウォリスの公式 Wallis's formulalim{(1/√n)·(2n)!!/(2n - 1)!!} = lim{(1/√n)·(22n(n!)2/(2n)!} = π Eq. スターリングの公式 Stirling's formula lim(Γ(s + 1)/(√(2π)·s(s+1)/2e-s) = 1 Th. B(p, q) = B(q, p) = B(p + 1, q) + B(p, q + 1) = (p + q)/p·B(p + 1, q)Pr. y = 1 - x (変数変換) B(p, q) = ∫01xp-1(1 - x)q-1dx = -∫10(1 - y)p-1yq-1dy = ∫01(1 - y)p-1yq-1dy = ∫01xq-1(1 - x)p-1dx = B(q, p) // |
[多くのTh.は既述Th.からの拡張]
|
Th. 収束N.C.: Σan 収束 ⇒ liman = 0 Ex. Σn=1∞(2n3/(n3 + 1)), lim(2/(1 + 1/n3)) = 2 (≠ 0) ∴ 発散 ⇔ 逆は真とは限らない: 逆 liman = 0 ⇒ Σan 収束 Ex. Σn=1∞an = Σn=1∞(1/(√n + √(n + 1)))
liman = lim(1/(√n + √(n + 1))) = 0 (しかし以下の通り発散) (√(n + 1) - √n)/((n + 1) - n) = √(n + 1) - √n = √(n + 1) - √n
Sn = Σk=1∞(√(k + 1) - √k) = √(n + 1) - 1 ⇒ |an+1 + an+2 + … + am| < ε [Σan → liman = 0] Pr. trivial (Cauchyの収束定理)Def. 正項級数 (positive term series, PTS): Σan, an ≥ 0 for ∀n Def. 絶対値級数 (absolute series) Σ|an| Def. 交項級数/交代級数 (alternating series)Σan 項が交互に正負 Ex. a1 – a2 + a3 – … (an > 0) Th. (ライプニッツの定理) {an}, an > 0 単調減少数列, liman = 0⇒ 交項級数 Σn=1∞(-1)n-1an 収束 Pr. Sn := Σk=1nak, a2k - a2k+1 ≥ 0 →S2n = a1 - a2 + a3 - a4 + a5 - … - a2n-2 + a2n-1 - a2n
= a1 - (a2 - a3) - (a4 - a5) - … - (a2n-2 - a2n-1) - a2n ≤ a1 → S2n+2 = S2n + a2n+1 - a2n+2 ≥ S2n → {S2n} 単調増加 → S := limS2n
→ limS2n+1 = → lim(S2n + a2n+1) = S + 0 = S Case 交項級数 a1 > a2 > … > an > … > 0, liman = 0 Th. 正項級数の比較判定法: [1, ∞) f(x) > 0 continuous, 単調増加 ⇒ Σn=1∞f(n), ∫1∞f(x)dx 同時に収束・発散 Def. 一般調和級数 ≡ Σn=1∞(1/nα) (α > 0)Σn=1∞an 正項級数 ⇒ Th. コーシー・アダマール判定法 Cauchy–Hadamard test: limn√an = r ⇒
i) 0 ≤ r < 1 → Σn=1∞an 収束,__ii) 1 < r ≤ ∞ → Σn=1∞an 発散
i) 0 ≤ r < 1 → Σn=1∞an 収束,__ii) 1 < r ≤ ∞ → Σn=1∞an 発散 lim{(n + 1)n+1/(n + 1)!·n!/nn} = lim(1 + 1/n)n = e (< 1) 収束 Th. ラーベ判定法 Raabe's test: limn(an+1/an - 1) = r ⇒i) -∞ ≤ r < -1 → Σn=1∞an 収束, __ii) -1 < r → Σn=1∞an 発散 Ex. Σn=1∞(1/n2): an := 1/n2 → n(an+1/an - 1) = n(n2/(n2 + 2n + 1) - 1)= (-2n2 - n)/(n2 + 2n + 1) = -2 (< -1) ∴ 収束 Th. Cauchyの凝集判定法 a1 ≥ a2 ≥ … ≥ an ≥ … ≥ 0⇒ Σn=1∞an, Σk=0∞2ka2k 同時に収束・発散 Pr. sn = a1 + a2 + … + an, tk = a1 + 2a2 + … + 2ka2k, 2k ≤ n < 2k+1 →sn ≥ a1 + a2 + (a3 + a4) + … + (a2k–1+1 + … + a2k) ≥ 1/2·a1 + a2 + 2a4 + … + 2k–1a2k = 1/2·tk sn ≤ a1 + (a2 + a3) + … + (a2k + … + a2k–1) ≤ 1/2·a1 + a2 + 2a4 + … + 2k–1a2k = tk
1/2·tk ≤ sn ≤ tk (2k ≤ n < 2k+1) Th. Σ|an| = s ⇒ Σan 絶対収束級数 → 収束 (Σan 収束, Σ|an| 発散 → Σan 条件収束級数) Pr. ∃ε > 0, 十分大きいm, n,|an+1 + an+2 + … + am| < |an+1| + |an+2| + … + |am| < ε // Ex. Σ(sinn/n2): |sinn/n2| ≤ 1/n2, Σ(1/n2) 収束∴ Σ|sinn/n2| 収束 (比較判定法) ∴ Σ(sinn/n2) 絶対収束 Th. 絶対収束級数は項の順序を変えても和は変わらない, Σan = ΣbnPr. 絶対収束級数 s := a1 + a2 + … + an + …,
sの項の順序を変えた級数 t := b1 + b2 + … + bn + … tr = b1 + b2 + … + br (r ≥ p ≥ q) → |sp – tq| ≤ |b1| + |b2| + … + |br| ∃ε > 0, N > q → |bq+1| + |bq+2| + … + |br| < ε ∴ |sp – tq| < ε // |
Th. [Riemann] 条件収束級数 Σan, ∃C (Real)
→ 項の順序を変えてできた級数が和Cを持つようにできる Pr. 正の項 p1, p2, …, 負の項 q1, q2, …,Σn=1∞pn & Σn=1∞(–qn) → ∞ (発散) m1: p1 + p2 + … + pm1–1 ≤ C < p1 + p2 + … + pm1 ≡ P1 n1: P1 – (q1 + q2 + … qn1–1) ≥ C > P1 – (q1 + q2 + … qn1–1 + qn1) ≡ Q1 m2: Q1 + pm1+1 + … + pm2–1 ≤ C < Q1 + pm1+1 + … + pm2–1 + pm2 ≡ P2 n2: P2 – (qn1+1 + … + qn2–1) ≥ C > P2 – (pn1+1 + … + pn2–1 + pn2) ≡ Q2 以下同様にm1, m2, …およびn1, n2, …の2組の数列を得る an → 0, pn → 0, qn → 0 ∴ {Pn}, {Qn} converge
∴ p1 + p2 + … + pm1 [級数の加法は普通の加法と同様に扱える] Pr. tn (Σ|aibj|の第n項の部分和)
≤ Σi=1p|ai|·Σj=1q|bj| 収束 (p, q: tnのai, bj中最大) → 正項級数 Σ|aibj|は収束
Σaibjの第n2部分和は(a1 + a2 + … + an)(b1 + b2 + … + bn)と並べ替えられ(a1b1 + a2b1 + a1b2 + a2b2 + … + anbn)とすると Σn=0∞an, Σn=0∞bn, cn = Σk=0nakbn-k ⇒ Σn=0∞cn Th. Σn=0∞an, Σn=0∞bn 絶対収束 ⇒ Σn=0∞cn 絶対収束(Σn=0∞an)(Σn=0∞an) = Σn=0∞(Σk=0∞akbn-k) 関数列 sequence of functionsDef. {fn}, f, ∃x ∈ I fixed, limf(x) 収束, f(x) = limfn(x) (x ∈ I) ⇒f ≡ {fn}の極限関数, {fn}はfに各点収束, I ≡ 収束域 Ex. I = [0, 1], fn(x) = xn → f(x) = limxn = 0 (0 ≤ x < 1), or 1 (x = 1)
⇒ lim{limfn(x)} ≠ lim{limfn(x)} Def. (一様収束) {fn}, f, ε > 0, N(ε) exist, ∃x ∈ I, ∃n ≥ N(ε), |fn(x) - f(x)| < ε ⇒ {fn}はfに一様収束 ≡ limsup|fn(x) - f(x)| = 0 Th. {fn} continuous on I → fに一様収束 ⇒ f continuous on IPr. ∃ε > 0, ∃N(ε/3) at ε/3 > 0, x ∈ I, n ≥ ∃N(ε/3) ⇒ |fn(x) - f(x)| < ε/3 Nε := N(ε/3) → |fNε(x) - f(x)| < ε/3 → fNε continuous on x = a → δ1(ε/3) > 0 exist → |x - a| < δ1(ε/3) ⇒ |fNε(x) - fNε(a)| < ε/3 δ(ε) := δ1(ε/3), |x - a| < δ(ε), ∃x ∈ I → |f(x) - f(a)| ≤ |f(x) - fNε(x)| + |fNε(x) - fNε(a)| + |fNε(a) - f(a)| < ε/3 + ε/3 + ε/3 = ε ∴ f continuous on x = a → ∃a ∈ I ∴ f continuous function on I // Th. 極限(一様収束) ⇔ 定積分: I = [a, b], {fn} fに一様収束 ⇒lim∫abfn(x)dx = ∫abf(x)dx Th. {fn} on I, C1-class → fに各点収束, {f'n} → gに一様収束 ⇒f on I, C1-class, f' = g ⇒ d/dx(limfn(x)) = limf'n(x) Def. 広義一様収束 ≡ {fn}はfにI上で一様収束しない, J ⊂ I, J上で一様収束Def1. {fn}, Sn(x) := Σk=1nfk(x), {sn} 各点収束, I 収束域 ⇒ 関数項級数 ≡ Σk=1nfn(x) := limSn(x) (x ∈ I) Def2. Tn(x) := Σk=1nfk(x) → {Tn} 各点収束 ⇒ Σk=1∞は絶対収束Def3. {fn}, 部分和 Sn(x) = Σk=1nfk(x) → {Sn} I上で一様収束 ⇒ Σn=1∞fn ≡ 一様収束 on I Th. ワイエルシュトラウスのM判定法 Weierstrass M-test{fn} → |fn(x)| ≤ Mn (x ∈ I), Σn=1∞Mn 収束, {Mn} exist ⇒ Σn=1∞fn I上で絶対収束かつ一様収束 Pr. Σn=1∞|fn(x)| 収束 (比較判定法) ∴ Σn=1∞fn 絶対収束|Σn=1∞fn(x) - Σn=1mfn(x)| = |Σn=m+1∞fn(x)| ≤ Σn=m+1∞|fn(x)| ≤ Σn=m+1∞Mn Σn=1∞Mn 収束 → sup|Σn=1∞fn(x) - Σn=1mfn(x)| ≤ Σn=m+1∞Mn → 0 (m → ∞) ∴ Σn=1∞fn 一様収束 // Def. 優級数 ≡ Σn=1∞Mn→ ワイエルシュトラウスのM判定法 ≡ 優級数判定法 |
|
Def. 整級数 Σn=0∞anxn = a0 + a1x + a2x2 + … + anxn + …
(ai = 1 → |x| < 1, 収束値 = 1/(1 – x)) [収束 → 値はxの関数] Th. 収束半径(r): Σanxn 整級数,
x = x0 (≠ 0)で収束, |∀x| < |r| ⇒ 絶対収束
→ Σ|anxn| 収束 → Σanxn, |x| = x0 絶対収束 ⇒ 収束半径 = r (r = ∞でも成立) Pr. r ≠ 0, ∞, lim|an+1xn+1/anxn| = lim|an+1/an||x| = |x|/r
∴ |x|/r < 1 → 収束, |x|/r > 1 → 発散 Pr. |∃x0 + h| < ρ < r, Σn=0∞anρn 絶対収束
∴ Σn=N+1∞|anρn| < εなるNを決めることができる ≤ |Σn=0Nan{(x0 + h}n – x0n| + 2ε
Σn=0Nan: xに関するN次多項式 → x = x0 continuous Th. Σn=0∞an 収束 ⇒ Σn=0∞anxn 一様収束 [0, 1] ⇒ Abelの連続性定理 (Abel's continuity theorem) Th. 項別積分定理 term-by-term integration theoremf(x) = Σn=0∞anxn, r > 0, |u| > r ⇒ ∫0uf(x)dx = ∫0uΣ(anxn)dx = Σ∫0uanxndx = Σn=0∞(an/(n + 1))un+1 |
Pr. f(x) = Σn=0∞anxn = Σn=0Nanxn + Σn=N+1∞anxn = Σn=0Nanxn + RN(x)
∫0uf(x)dx = ∫0u(Σn=0Nanxn)dx + ∫0uRN(x)dx Σn=N+1∞|anxn| ≤ Σn=N+1∞|anxnun| ≤ Σn=N+1∞|anxn|ρn
→ 収束 → Σn=N+1∞|anxn| < ε
εはNが大きくなればいかほどでも小さくできる lim{∫0uf(x)dx – Σn=0Nan/(n + 1)·un+1} = lim∫0uRN(x)dx = 0 → ∫0uf(x)dx = Σn=0∞(an/(n + 1))un+1 |x1| > r, if Σn=0∞an/(n + 1)·x1n+1 → 収束 → |an/(n + 1)·x1n+1| < ∃M (n = 1, 2, …)
|x| < |x1| ≤ M·(n + 1)/|x1|·|x/x1|n |x/x1| < 1 ∴ Σ(n + 1)/|x/x1|n → 収束 ⇔ r < |x| < |x1|, rがΣanxnの収束半径であることと矛盾
∴ Σan/(n + 1)xn+1はr < |x|なるxに対して発散 f(x) = Σn=0∞anxn, r (> 0), |x| < r → f'(x) = Σn=0∞nanxn-1 Pr. g(x) := Σn=0∞nanxn–1, 項別積分定理より∫0ug(x)dx = f(u) – a0 → 両辺をuについて微分: g(u) = f'(u), u = x // 拡張 f(k)(x) = Σn=0∞n(n – 1) … (n – k + 1)anxn-k, |x| < rTh. |f(n)(x)| < M for ∀n → f(x) = Σn=0∞(f(n)(0)/n!)xn (Mはxに依存) Pr. |(f(n)(ξ)/n!)·xn| < M·|xn|/n!, 整級数 Σn=0∞(xn/n!)の収束半径 = ∞ ∴ lim(xn/n!) = 0 ∴ lim(f(n)(ξ)/n!)·xn = 0 // Th._sinx = x – x3/3! + … + (-1)n–1{x2n–1/(2n – 1)!} + …,cosx = x2/2! + … + (-1){x2n/(2n!)} (-∞ < x < ∞) Pr. f(x) = sinx, f(n)(x) = sin(x + nπ/2), f(0) = sin(nπ/2)
∴ f(n)(0) = 1, 0, -1, 0, 1, 0, -1, … (n = 1, 2, 3, …) |
|
周期性をもつ関数の(無限の)和により表したもの → フーリエ解析: フーリエ級数を用いた解析 Ex. フーリエ変換 画像処理、データ圧縮、CT、MRI等の基礎技術として発展 Ax. (三角関数の直交性) m, n ∈ N ⇒
∫-ππsinmxcosnxdx = 0 … (1)
= π (m = n)
∴ (1) trivial |
i) m = n → ∫-ππsin2mxdx = ∫0π(1 - cos2mx)dx = [x - sin2mx/2m]0π = π
_ ∫-ππcos2mxdx = ∫0π(1 + cos2mx)dx = [x + sin2mx/2m]0π = π ii) m ≠ n → ∫-ππsinmxsinnxdx= [sin(m - n)x/(m - n) - sin(m + n)x/(m + n)]0π = 0 _ ∫-ππcosmxcosnxdx = [sin(m + n)x/(m + n) + sin(m - n)x/(m - n)]0π = 0 // |
Def. 領域 domain: (a1, a2), (b1, b2) ∈ A, [0, 1],
φ(t), ψ(t) continuous ⇒ Def. 閉領域: 境界を全て含む領域 Ex. x2 + y2 ≥ 0 Def. 極限値 Pn(xn, yn), 点列{Pn}, {Pn} ⇒ A(a, b) ⇔ ∀ε, ∃n0 < 0, limf(x, y) = c Pr. √{(a – xn)2 + (b – yn)2} < ε → |a – xn| < ε and |b – yn| < ε
逆に|a – xn| < ε, |b – yn| < ε → √{(a – xn)2 + (b – yn)2} < ε < √2·ε < 2ε Th1. 部分集合K (≠ ∅)が閉集合 (N.S.C.) ⇒ xn ∈ K, limxn = a → a ∈ K Th2. 部分集合K (≠ ∅)が閉集合 (N.S.C.) ⇒ Kc 開集合 |
Def. 類似極限 repeated limit: lim{limf(x, y)}, lim{limf(x, y)} Def. 偏微分Aのδ近傍内全ての点Pについて進路に無関係
(= A点からP点に近づく方法に無関係) lim{f(a + h, b) – f(a, b)}/h = fx(a, b) = ∂f/∂x → f(x, y)の(a, b)におけるxに関する偏微(分)係数 lim{f(a, b + h) – f(a, b)}/h = fy(a, b) = ∂f/∂y → f(x, y)の(a, b)におけるyに関する偏微(分)係数 Ex. f(x, y) = x/(x + y)のfx, fy: fx (fy)を求める間はy(x)を定数と考えるfx = y/(x + y)2, fy = -1/(x + y)2 Def. fx, fy exist ⇒ 偏微分可能Def. 方向微分 lim{f(a + rcosθ, b + rsinθ) – f(a, b)}/r = df/drθ (0 ≤ θ < π)
θなる方向についての偏微分係数 in (a, b) → |
|
Def. C1-class: f(x, y) on D 偏微分可能, fx(x, y), fy(x, y) continuous
⇒ f(x, y)はDでC1-class 微分間の関係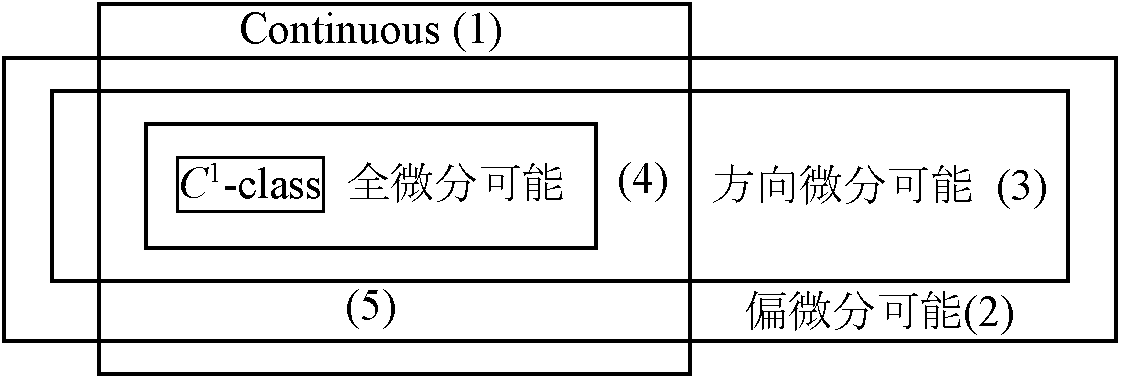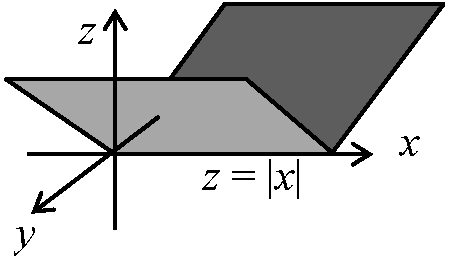 
(1) 連続で偏微分可能ではない 凡例 z = |x|(2) 方向微分可能 ⇒ 偏微分可能
明らかにθ = 0, θ = π/2のときそれぞれの方向微分値が偏微分となる ∵ y = mxに沿って(0, 0)に近づく limf(x, mx) = lim{2mx2/(1 + m2)} = 2m/(1 + m2) ≠ 0 (m ≠ 0のとき)不連続 in (0, 0) 
(3) 方向微分可能、不連続凡例 f(x, y) = 2xy/(x2 + y2) for (x, y) ≠ (0, 0), or _________= 0 for (x, y) = (0, 0) in (0, 0) Pr._lim(f(h, 0) – f(0, 0))/h = lim(0 – 0)/h = 0
0 = fx(0, 0), 0 = fy(0, 0) ∴ fx(0, 0), fy(0, 0) → parted diff. = lim2sinθcosθ/r = limsin2θ/r θ = 0, π/2のとき方向微分可能ではない → limf(x, y) = 0, f(0, 0) = 0 Def. 全微分可能 totally differentialf(x, y): D ∋ (a, b), (a + h, b + k),
f(a + h, b + k) - f(a, b) = A(a, b)h + B(a, b)k + ε(h, k)·√(h2 + k2), limε(h, k) = 0 ⇒ f(x, y) is totally differential in (a, b) Th. [1-3] f(x, y), (a, b) totally diff. ⇒[1] (a, b) continuous, [2] fx, fy exist, [3] f(x, y) (a, b) 方向微分可能 Pr._[1] trivial [2] k := 0, (f(a + h, b) – f(a, b))/h = A(a, b) ± ε(h, 0)
h → 0, fx(a, b) = A(a, b), k = 0, fy(a, b) = B(a, b) [3] h = rcosθ, k = rsinθ, f(a + rcosθ, b + rsinθ)/r = fx(a, b)cosθ + fy(a, b)sinθ ± ε(rcosθ, rsinθ) h → 0 → ε → 0, df/drθ=fx(a, b)cosθ + fy(a, b)sinθ Ex. 全微分可能でないもの f(x, y) = √|xy| in (0, 0)Pr._lim(f(0 + h, 0) - f(0,0))/h = lim(0 - 0)/h = 0
∴ (0, 0)でxについてfx(0, 0) = 0となり偏微分可能。一方、 ε(x, mx) = √(m/(1 + m2)) = √(1/2) (m = 1) よって全微分可能ではない Th. fx, fy exist, fx, fy continuous (= C1-class) ⇒ f(x, y)は全微分可能Pr._f(a + h, b + k) – f(a, b)
= f(a + h, b + k) – f(a, b + k) + f(a, b + k) – f(a, b) = fx(a, b)h + fy(a, b)k + {(ε1h + ε2k)√(h2 + k2)}/√(h2 + k2) (ε1h + ε2k)/√(h2 + k2) = ε(h, k), |ε1h/√(h2 + k2)| < |ε1|·|h|/√(h2 + k2) < |ε1| |(ε1h + ε2k)/√(h2 + k2)| < |ε1h/√(h2 + k2)| + |ε2k/√(h2 + k2)| < |ε1| + |ε2| → 0 (h, k) → (0, 0) Ex. z = f(x, y) = x2 + y2, A(1, 2, f(1, 2))における接平面の方程式
C1-class - totally diff., fx(x, y) = 2x, fy(x, y) = 2y 高次導関数 (high-order derivatives)lim(fx(a + h, b) – fx(a, b))/k = fxx(a, b),lim(fx(a, b + k) – fx(a, b))/k = fxy(a, b)などfxx, fxy, fyx, fyyを考える 更に、高次偏導関数を考える (一般にfxy ≠ fyx) Ex. f(x, y) = [xy(x2 – y2)]/(x2 + y2) in (x, y) ≠ (0, 0), = 0 in (x, y) = (0, 0) Def. Δf(x, y) = fxx(x, y) + fyy(x, y) ⇒ f(x, y)のラプラシアン (Laplacian) Def. 調和関数: 定義域でΔf(x, y) = 0を満たす or fxx + fyy = 0となる関数 Q. f = log√(x2 + y2) = 1/2·log(x2 + y2) のfxx + fyy A. fx = 1/2·2x/(x2 + y2) = x/(x2 + y2) fy = y/(x2 + y2)
fxx = (x2 + y2 + y2)/(x2 + y2)2 = (y2 - x2)/(x2 + y2)2 [1] f(x, y): C2-class__[2]の拡張 ∵ [1] fxx, fxy, fyx, fyy: exist, continuous [2] Youngの定理 fxy, fyx exist, continuous [3] fx, fy exist, totally diff. 偏微分可能 → fxx, fxy, fyx, fyy 存在 (連続の仮定なし) [4] Schwarzの定理 fx, fy, fxy exist, fxy continuousPr._ [2] Δ = f(a + h), b + k) - f(a + h, b) - f(a, b + k) + f(a, b)
φ(x) ≡put f(x, b + k) - f(x, b) = h[fx(a + θ1h, b + k) - fx(a + θ1h, b)] = hkfxy(a + θ1h, b + θ2k)
limΔ/hk = limfxy(a + θ1h, b + θ2k) = fxy(a, b) fxy: 連続 = hkfyx(a + θ4h, b + θ3k) = fyx(a, b) fyx continuous Pr._[3] h := k → Δ = h[fx(a + θ1h, b + k) - fx(a + θ1h, b)] fx: to (a + h, b + k)fx(a + θ1h, b + h) – fx(a, b) = fxx(a, b)θ1h + fxy(a, b)h + ε(a1h, h)√{(θ1h)2 + h2} … (1) fx(a + θ1h, b) – fx(a, b) = fxx(a, b)θ1h + fxy(a, b)·0 + ε(a1h, 0)√{(θ1h)2 + 02} … (2)
(1) – (2): Δ = h2[fxy(a, b) ± ε(θ1h, h)√(θ12 + 1) ∓ ε(θ1h, 0)|θ1|]
→ lim(Δ/hk) = 1/h·[fy(a + h, b) – fy(a, b)] ∂nf/∂xn, ∂nf/∂xn-1∂y, ∂nf/∂xn-2∂y2, …, ∂nf/∂x∂yn-1, ∂nf/∂yn の何れかと一致 高次偏導関数 (high-order partial derivative)(1) z = f(x, y), x = x(t), y = y(t) ⇒ z = f(x(t), y(t)) cp. Taylorの定理Pr._dz/dt = ∂f/∂x·dx/dt + ∂f/∂y·dy/dt d2z/dt2 = (fxx·dx/dt + fxy·dy/dt)dx/dt + fx·d2x/dt2 + (fyx·dx/dt + fyy·dy/dt)dy/dt + fy·d2y/dt2 = fxx(dx/dt)2 + 2fxy(dx/dt·dy/dt) + fyy(dy/dt)2 + fx(d2x/dt2/) + fy(d2y/dt2) (2) z = f(x, y), y = y(x) → z = f(x, y(x))Pr._dz/dx = ∂f/∂x·dx/dx + ∂f/∂y·dy/dx = fx + fy·(dy/dy) d2z/dx2 = fxx·dx/dx + fxy·dy/dx + (fyx·dx/dx + fyy·dy/dx)dy/dx + fy·d2y/dx2 = fxx + 2fxy·dy/dx + fyy(dy/dx)2 + fy·d2y/dx2 (3) z = f(x, y), x = x(t), y = y(t) → dz/dt = fx·dx/dt = fy·dy/dtd2z/dt2 = fxx(dx/dt)2 + 2fxy·dx/dt·dy/dt + fyy(dy/dt)2 
+ fx·d2x/dt2 + fy·d2y/dt2
{z = f(x, y), x = a + ht, y = b + kt}
Cn-classでD ∋ (a, b), (a + h, b + k)に対して
+ 1/2!·(h·∂/∂x + k·∂/∂y)2·f(a, b) + … (a, b) := (0, 0), (h, k) := (x, y) → Maclaurinの展開 Pr. x := a + ht, y := b + kt,
f(a + ht, b + kt) ≡put φ(t): Maclaurin条件を満足する + (φn–1(0)/(n – 1)!)/tn-1 + (tn/n!)φ(θt) φ(n)(t) =(h·∂/∂x + k·∂/∂y)n·f(a + ht, b + kt) ここでt := 1 |
Th. (漸近展開) f(x, y) Cn-class in nbh (a, b), (∃x, ∃y) ⇒
f(x, y) = Σl=0nΣj=0l(lCj/l!)·(∂lf/∂xj∂yl-j)(a, b)(x - a)j(y - b)l-j + ο(rn) (r = √((x - a)2 + (y - b)2) → 0) Ex. n = 2, (0, 0) →f(x, y) = f(0, 0) + fx(0, 0) + fy(0, 0) + 1/2{fxx(0, 0)x2 + 2fxy(0, 0)xy + fyy(0, 0)}y2} + ο(r2) (r = √((x - a)2 + (y - b)2) → 0) Th. α: ∀Real, t ≠ 0, f(tx, ty, tz) = tαf(x, y, z) 三次⇒ f(x, y, z) α次の斉次(同次)関数 homogenous function Ex. fx(x, y) ≡ fy(x, y) ≡ 0 → f(x, y) constantPr. f(x, y) = f(0, 0) + xfx(θx, θy) + yfy(θx, θy) = f(0, 0) = constant Th. Eulerの定理: (0, 0, 0)を含まない領域 f(x, y, z) α次のhomog. fn ⇔ x·∂f/∂x + y·∂f/∂y + z·∂f/∂z = αf(x, y, z) x → tx, y → ty, z → tz → xfx + yfy + zfz = αf(x, y, z) Pr. N.C. f(tx, ty, tz) = tαf(x, y, z): tでdiff.,
fx(tx, ty, tz)x + fy(tx, ty, tz)y + fz(tx, ty, tz)z = αtα-1f(x, y, z) 合成関数の偏微分 (partial differentiation of composite function)偏導関数の応用 (application of partial derivative)Def. δ > 0 十分小さいδ, √(h2 + k2) < δ, ∀h, ∀k
f(a + h, b + k) < f(a, b) at U(a, b) → 極大 ⇒ 極大値 ≡ f(a, b) Def. f(x, y) ≤(≥) f(a, b) ⇒ f(x, y) ≡ 広義の極大(小) Th. 極値のN.C. fx, fy continuous, f(x, y) 極大or 極小 in (a, b) ⇒ fx(a, b) = 0, fy(a, b) = 0 Pr. x = a 極値 ∴ fx(x, b) = 0 at x = a ∴ fx(a, b) = 0, fy(a, b)も同様Th. fx(a, b) = fy(a, b) = 0 ⇒ 滞留点(臨界点) ≡ (a, b) ⇔ 鞍点 ≠ 極小/極大 Th. 極値のS.C. fx(a, b) = fy(a, b) = 0, fxx, fxy, fyy continuous, D ≡ h2fxx(a, b)A + 2hkfxy(a, b)B + k2fyy(a, b)C i) AC – B2 < 0,AD = A2h2 + 2ABhk + ACk2 = (Ah + Bk)2[> 0] + (AC – B2)[> 0]k2[> 0] ∴ AD > 0
→ A > 0, D > 0, f(a, b) 極小
Ah + Bk ≠ 0, k = 0 A. z = a – x – y, xyz = xy(a – x – y), f(x, y) := xy(a – x – y),
fx = y(a – 2x – y) = 0, fy = x(a – x – 2y) = 0 ⇒ y = f(x) 一価関数 exist in nbh at x = a, b = f(a), F(x, f(x)) = 0, dy/dx = -Fx/Fy Ex. x2 + 2xy + 2y2 – 1 = 0, dy/dx
→ f(x, y) = x2 + 2xy + 2y2 – 1, fx = 2x + 2y, fy = 2x + 4y A. xで微分 → 6x2 + 12xy + 6x2y' - 4y - 4xy' + 6yy' = 0
∴ 2(3x2 - 2x + 3y)y'= -6x2 - 12xy + 4y 特異点と曲面f(x, y) = 0, fx, fy continuous in (a, b) ⇒Def. 通常点 (ordinary point) fx(a, b) ≠ 0
→ (dy/dx)x=a = -(fx(a, b)/fy(a, b)), fy(a, b) ≠ 0 Case. (0, 0)が特異点 f(0, 0) = 0, fx(0, 0) = 0, fy(0, 0) = 0
Maclaurin展開 + 1/3!(x·∂/∂y + y·∂/∂y)3f(0, 0) + … [類推] f(a, b) = ax2 + 2bxy + cy2 + px3 + 3qx2y + 3rxy2 + sy3 + … (a = 1/2gxx(0, 0), b = 1/2gxy(0, 0), c = 1/2gyy(0, 0) …)
媒介変数表示 x = lt, y = mt φ(x, y) diff. in nbh (a, b), C1-class, φ(0, 0) = 0, (a, b) ≠ φ(x, y)の特異点 φ(x, y) = 0, f(x, y) (a, b)で極値 totally diff. ⇒ λ exist, fx(a, b) + λφx(a, b) = 0, fy(a, b) + λφy(a, b) = 0 Pr. φx(a, b) ≠ 0 or φy(a, b) ≠ 0 (∵ (a, b) ≠ φ(x, y) = 0の特異点)Case. φx(a, b) ≠ 0: φ(x, y) = 0 , y = η(x) C1-class in nhb a, b = η(a) exist
g(x) = f(x, η(x)) → x = aで極値 → g'(a) = 0 = fx(x, η(x)) - fy(x, η(x))·{φx(x, η(x))/φy(x, η(x))}
b = η(a) → g'(a) = fx(a, b) - fy(a, b)/φy(a, b)·φx(a, b) = 0 fx(a, b) + λφx(a, b) = 0, fy(a, b) + λφy(a, b) = 0 // Def. ラグランジュの未定乗数 ≡ λDef'. 特異点 (singular point) φ(x) C1-class, φ(x) = 0,
φ(a) = φx1(a) = φx2(a) = … = φxn(a) = 0 ⇒
a ≠ φ(x)の特異点, f(x) aで極値, totally diff. (φ(x) = 0) ⇒ ∇f(x1, x2, … xn) = (fx1(x1, x2, … xn), fx2(x1, x2, … xn), … fxn(x1, x2, … xn)) ⇒ f(x1, x2, … xn)の勾配 [∇f(x)またはgradf(x)と表記] Def''. 特異点(複数): φ1(x), φ2(x), … φm(x) C1-class, a = (a1, a2, … an)
φ1(a) = φ2(a) … φm(a) = 0,
∇φ1(a), ∇φ2(a), …, ∇φm(a) (1次従属)
C1-class in nbh a = (a1, a1, …, an), φ1(a) = φ2(a) = … = φn(a) = 0 ∂f/∂xj·(a) = Σi=1m{λ(·∂φi/∂xj·(a)} = 0 (j = 1, 2, …, n) Ex. x2 + y2 = 2, f(x, y) = xyの最大値と最小値Ex. 半径rの球に内接する直方体の体積の最大値 2重点 al2 + 2blm + cm2 = 0, D = b2 – ac
漸近線: 無限分枝に沿い原点から無限に遠ざかる、この点から一定直線gまでの距離PH → 限りなく0となる曲線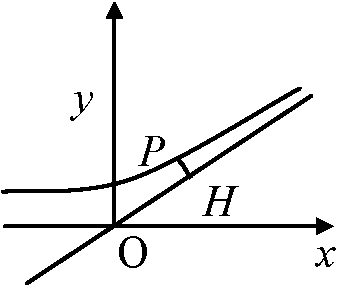 
g:y = mx + c → y軸に平行でない漸近線PH = |y – mx – c|/√(1 + m2) Pが曲線上を原点から無限に遠ざかる → ____lim|y – mx – c|/√(1 + m2) = 0, ____lim(y – mx – c) = 0
∴ limy/x = m → mが求まった
∴ c = lim(y – mx) → cが求まった 
A._1 – 3ay/x2 + (y/x)3 = 0, m = limy/x
→ lim(1 – 3a/x·m + m3) = 0 ∴ m = –1 → m = 3√2 → y = 3√4·a (極大), m = 0 → y = 0 (極小) Ex. 柱面の一般方程式: F(y – mx, z – nx) → 接平面は全て一定直線に平行 Pr._α = y – mx, β = z – nx, (x, y, z)における接平面
→ (-mFα – nFβ)(X – x) + Fα(Y – y) + Fβ(Z – z) = 0 |
二重積分(2変数関数の積分)Def. f(x) [a, b], Δ: a = x0 < x < … < xn-1 < xn = b, [xi–1, xi] ∋ ξi,
xi – xi-1 = ξi, limΣi=0nf(ξi)δi = I exist → Mi max, sΔ = Σmiδi → mi min, S(infSΔ) = s(supsΔ) Th. f(x): [a, b] continuous ⇒ 一様連続 ⇒ integrablePr. Δ分割, 細区間δiにおける振動量(Mi – mi = vi)
SΔ – sΔ = Σiviδi, limΣiviδi = lim(SΔ – sΔ) = S – s
⇒ ∫k∫f(x, y)dxdy = ∫ab∫cdf(x, y)dydx = ∫cd∫abf(x, y)dxdy Pr. f(x, y) continuous → 一様連続 ωijを十分小さくとると(ωij < εにとれる) Mij – mij = vij (ωijにおける振動量)
Σi,jvijωij < Σi,jεωij = ε(b – a)(d – c) → ∀εであるからlimΣvijωij = 0 Pr. 平均値の定理よりmij(yj – yj–1)
≤ ∫yi-1yjf(ξi, y)dy ≤ Mij(yj – yj–1), Σjmij(yj – yj–1) ≤ ΣijMij(yj – yj–1)(xi – xi–1)·SΔ
supsΔ·s ≤ ∫ab∫cdf(x, y)dydx ≤ S·infSΔ → S = s = ∫∫kf(x, y)dxdy yをfixedすると同様に得られる // Th. f(x, y) continuous
→ F(x) = ∫cdf(x, y)dy continuous, f(x, y) continuous → 一様連続 F(x) = limF(x + Δx, y) 空間問題 (space)一般有界閉領域 D = (a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x))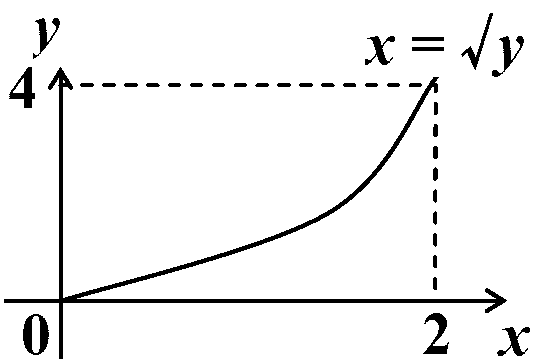
ωijが完全にDに含まれているとき Mij = mij = 1 = ∫cdf(x)[∫abf(x, y)dx]dy 累次積分
置換積分 x = u(x, y), y = v(x, y) → 全て点は不変 invariant
∴ ∂(x, y)/∂(u, v)·∂(u, v)/∂(ξ, τ) = ∂(x, y)/∂(ξ, τ) → S - s = SΔ – sΔ = 臨界領域の面積 K Def. 面積確定: δ → 0 → KΔ≡ 0 臨界領域が幾らでも小さい面積中に含められる Ex. Dの境界が滑らかな曲線 smooth curve あるいはそれらの有限の接合x = φ(t), y = Ψ(t), φ'(t), Ψ'(t): continuous (C1-class), φ'(t)2 + φ'(t)2 ≠ 0
→ 面積確定
K: a ≤ x ≤ b, c ≤ y ≤ d f(x, y) → S = ∫∫Kf(x, y)dxdy 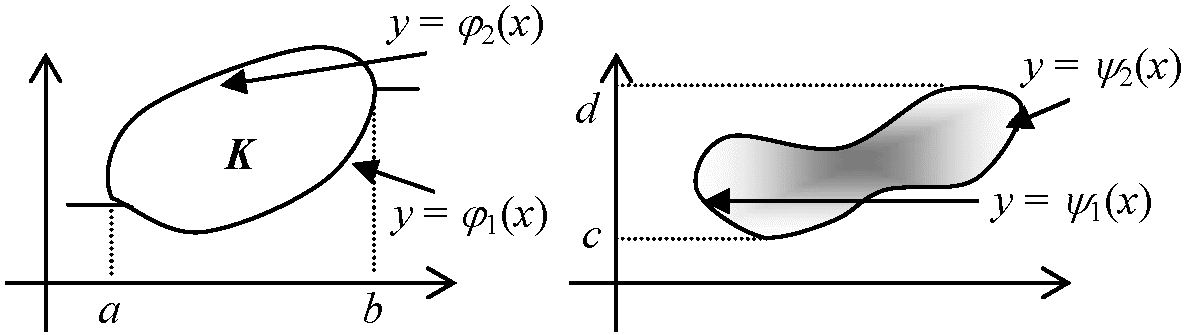 S = ∫ab(φ2(x) – φ1(x))dx________V = ∫cd(ψ2(x) – ψ1(x))dx |
Ex 1.________________________Ex 2.
Ex. ∫0c{(1 – x/a)·c – (1 – b/x)·c}dy Ex. 2次元 two-dimension における一次変換 linear transform
x = au + bv, y = cu + dv (a, b, c, d: constant) if J ≠ 0 → xy平面全体とuv平面全体とは1:1
Cf. 直線は直線、平行線は平行線に移る
前式に代入 S'' = ad - bc = J → Jに変換される Ex. 円柱座標 z = f(r, q) (r, θ, z)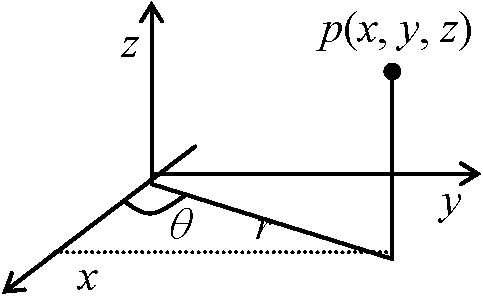
τ = acosθ, 0 ≤ θ ≤ π/2 J = ∂(x, y, z)/∂(r, θ, z) = r Ex. 極座標: 自由変数と従属変数との両方を変換する方法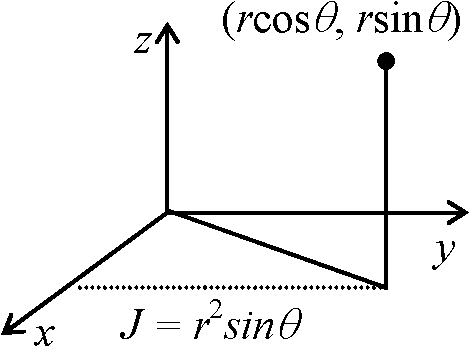
f(x, y) = f(rcosθ, rsinθ), f(rcosθ, rsinθ)Δσij (r, θ) ∈ (Δσij) Pr. f(x, y), ∂f/∂x, ∂f/∂y continuous z – zij = (x – ξi)fx(ξi, ηj) + (y – ηj)fy(ξi, ηj) 接平面をとったもの
この接平面とxy平面のなす角をrij (0 ≤ rij ≤ π/2) → Δσij = √(1 + fx(ξi, ηj)2 + fy(ξi, ηj)2)·ΔxiΔyj ∴ ΣΔσij = Σj=1nΣi=1m√{1 + fx(ξi, ηj)2 + fy(ξi, ηj)2}·ΔxiΔyj (1) surface z = f(x, y): S = ∫∫(D)√(1 + (∂z/∂r)2 + (∂z/∂θ)2)rdrdθ(2) 曲面 円柱座標: z = f(x, y), x = rcosθ, y = rsinθ 変数変換
zr = fxfr + fyfr = fxcosθ + fycosθ, 1/r·zθ = fx(-sinθ) + fy(cosθ) S = ∫∫D'√(1 + (∂z/∂r)2 + (1/r2)·(∂z/∂θ)2)rdrdθ, D': 極座標表示 (3) 曲面 x = f(x, y), y = x(u, v), z = y(u, v)
[zu = zxxu + zyyu, zv = zxxv + zyyv, zx = fx] → 第2基本量 Ex. x2 + y2 + z2 = a2の表(曲)面積 =
z = √(a2 – x2 – y2), = 8∫0π/2[–√(a2 – r2)]0adθ = 8a∫0π/2adθ = 4πa2 Ex. 楕円 x2/a2 + y2/b2 = 1 (0 < b < a)をx軸の回りに回転したときの表面積
y2 = b2/a2·(a2 – x2), 2y·dx/dy = –2(b2/a2)x
= 2πbe/a[1/2·x√{(a/e)2 – x2} + (a2/ae2)sin–1(ex/a)]–aa If a = b → S = 4πa2 多重積分/n重積分 (multiple integration)W = f(x, y, z), D (a ≤ x ≤ b, c ≤ y ≤ d, e ≤ z ≤ f)
Σk=1nΣj=1mΣi=1l(ξi, ηj, ςk)Δijk((ξ, η, ς) ∈ ΔDijk) → 0 ⇑ 円柱座標 x = rsinθcosθ, y = rsinθsinθ, z = rcosθ Ex. 球 x2 + y2 + z2 = a2 の表(曲)面積と体積A. S = 4a2π, V = 4/3·πa3 |
|
独立変数、従属変数、従属変数の微分係数を含む式 さまざまな自然現象や社会現象を記述 Ex. 落下運動の方程式 d2x/dt2 = -g, x: 物体の高さ, g: 重力加速度 Ex. 振子の運動方程式l·d2θ/dt2 = -gsinθ, l: 紐の長さ, θ: 下向き垂直方向からの角度 Ex. 惑星の運動方程式Ex. ロジスティック式(個体群成長) Ex. Lotka-Volterra式 (捕食者-被捕食者モデル) Def. ラプラス変換 Laplace transform, F(s): f(t) [0, ∞] integrable, F(s) = ∫0∞f(t)e-stdt converge on s ∈ ℜ ⇒ L[f(t)](s) = F(s) Def. 逆ラプラス変換, L-1: L[f(t)](s) = F(s) ⇒ L-1[F(s)](t) = f(t)Th. ラプラス変換可能十分条件
[0, ∞], f(t) continuous, α, M > 0 → |f(t)| ≤ Meαt (t ≥ 0) ⇒
∫0∞Me-(s-α)tdt = lim[-M/(s - α)·e-(s-α)t]t=0t=R ⇒ L[af(t) + bg(t)](s) = aL[f(t)](s) + bL[g(t)](s) |
Th. 導関数: f(t) [0, ∞) C1-class, α, M > 0 → |f(t)| ≤ Meαt (t ≥ 0)
⇒ L[f'(t)](s) = sL[f(t)](s) - f(0) スツルムリウビル方程式(Sturm-Liouville equation)の特別例Ax. (ルジャンドル多項式 Legendre polynomial), N →
Pn(x) := 1/2nn!·dn/dxn(x2 - 1)n ⇒
Ln(x) := ex·dn/dxn(xne-x) ⇒
Hn(x) := (-1)nex2·dn/dxne-x2 ⇒ |
|
Def.(常)微分方程式 F(x, y, y', y'' … y(n)) = 0
独立変数x、未知関数y及びその導関数y', y'' …, y(n)を含む方程式 Def. 解 = 常微分方程式を満足する関数y(x) 一般解 Ex. dy/dx = y, d2y/dx2 + y = 0 → dy/dx = y = Cex, y = Asinx + Bcosx (A, B, C: 任意定数, 積分定数) 初期条件 x = x0, y = y0 特別解(特殊解): 一般解の積分定数に特別な値を得て得られる解 基本型
|
Def. 変数分離形: F(x, y, dy/dx) = 0, dy/dx = f(x, y) = P(x)Q(y)
If Q(y) ≠ 0, 1/Q(y)·dy/dx = P(x) → ∴ x2 – y2 = A (A: 任意定数) → 一般解 Def. 同次(斉次)微分方程式 dy/dx = f(y/x)
⇒ dy/dx = f(x, y)の右辺がx, yの0次同次関数 A. dy/dx = (1 + y/x)/(1 - y/x), y := xu → u + x·du/dx = (1 + u)/(1 - u)
x·du/dx = (1 + u)/(1 - u) - u = (1 + u2)/(1 - u) |
|
Def. 線型微分方程式: y'とyについての一次式
p(x), q(x), dy/dx = p(x)y = q(x) y := u(x)v(x), dy/dx = du/dx·v + u·dv/dx, du/dx·v + u(dv/dx + pv) = qv(x): dv/dx + pv = 0, du/dx·v = q → v = Ae-∫pdx du/dx = q/v = q/A·e∫pdx → u = 1/A·∫qe∫pdxdx + B
y = uv = Ae–∫pdx(1/A∫qe∫pdxdx + B) = e–∫pdx(∫qe∫pdxdx + C) Ex. dy/dx + p(x)y = q(x)yn, n ≠ 0, 1: Bernoulliの方程式
y1 – n := v X(x, y), Y(x, y) → ∂X/∂y = ∂Y/∂x → 完全微分形 Ex. 3x2 + 6xy2 + (6x2y + 4y2)·dy/dx = 0
∫x0x(3x2 + 6xy2)dx + ∫y0y(6x02y + 4y2)dy = C クレローの常微分方程式 Clairaut's equationDef. y = x·dy/dx + f(dy/dxdy/dx := p → y = px + f(p) 両辺をxで微分
p = x·dp/dx + p + f'(p)·dp/dx ii) x = pf'(p) → y = f(p) - pf'(p)
x = -f'(p), and y = f(p) - pf'(p) → p := C ダランベールの常微分方程式 d'Alembert's equationDef. y = xf(y') + g(y')n階線形微分方程式Def. pn(x)·dny/dxn + pn–1(x)·dn–1y/dxn–1 + … + p1(x)·dy/dx + p0(x)y = f(x)p0(x) … pn(x) 関数 Def. 線形同次微分方程式: f(x) = 0 ⇒ Def. 同次形(斉次形): f(x) ≡ 0Def. 線形非同次微分方程式: f(x) ≠ 0 Def. n階線形微分方程式: 線形微分方程式に含まれる導関数の最高次数がn Ex. x3y''' + x2y'' + xy' + y = 0 → 3階線形微分方程式 Th. 一次独立な2つの解は基本解を形成するPr. y1(x), y2(x) 一次独立な2つの解 W(x): ロンスキー(Wronski or Wronskian)行列式を用いる |
Q. y'' + y = secxを解く A. y := eλx, λ2 + 1 = 0, λ = ±i ∴ e±ix, cosx, sinx 基本解 y = c1(x)cosx + c2(x)sinx, y' = -c1(x)sinx + c2(x)cosx, c1'(x)cosx + c2'(x)sinx = 0
y'' = -c1'(x)sinx + c2'(x)cosx – c1(x)cosx – c2(x)sinx 原式に戻す 連立線形微分方程式 system of linear differential equationn個の未知関数をもつ微分方程式の系X' = AX + F
X = Def. 微分方程式 F = 0 → 同次方程式 homogeneous equation 2つのn次正方行列 A, B, B = P-1AP
→ Aは正則行列Pによって変換された
→ Aの固有多項式 → Def. 固有値(特性値): Aの根
Y = AX + B, 2Y = 2AX + 2Bは等式 → Y = 2Y → 固有値 = 2  = 
X := Y (つまり平行) x + y = 0 → A: 固有値, (1,-1): 固有ベクトル Def. 相似な行列: B ≡ P-1AP (A: n次の正方行列, P: n次の正則行列)Th. 固有多項式: 相似な2つの行列は同じ固有多項式を持つ 逆は正しくない φA(λ) = φP-1AP(λ) Pr. φP-1AP(λ) = det(P-1AP - λI) = det(P-1AP - λP-1IP)
= det(P-1AP - P-1λIP) = det(P-1(A - λI)P) = |P-1||AP - λI||P| Pr. trivial (固有多項式が等しい) Def. 正値定符号と負値定符号: q
> 0 (正) - 正値定符号 positive definite |
変数変換法 |
|
Def. 虚数: x2 + 1 = 0 → x2 = –1 → x = √-1 ≡ i (i, 虚数単位)
i2 = -1, i3 = i × i2 = -i, i4 = 1, … Def. 複素数(z): z = x + iy (i2 = -1) → x: 実数部 real part, ℜ. y: 虚数部 imaginary part, ℑ
整数部: Re(z) or ℜz = x, 虚数部: Im(z) or ℑz = y |
Def. トレース trace: zz* = x2 + y2 (実数) Def. z – z* = 2iy (純虚数) Def. 絶対値absolute value: |z| ≡ √zz* = √(x2 + y2) Def. 複素数の四則演算: z1 = x1 + y1i, z2 = x2 + y2i →
加減則 (シュプール spur): z1 ± z2 = (x1 ± x2) + (y1 ± y2)i Re(z1z2) ≠ Re(z1)Re(z2) 除法即 (ノルム norm): z1/z2 = (x1x2 + y1y2)/(x22 + y22) + (–x1y2 + y1x2)/(x22 + y22)i Th. z1 = z2 ⇔ x1 = x2, y1 = y2→ 複素数全体は加減乗除演算に閉じた集合 |
= 0 → 
- 平行線は平行線に移る
, A = 
, F = 
→ AP = PΛ
,
→ ガウス平面: 複素数を表わすため用いる座標平面