(2019年1月10日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 成長
|
そもそも … 「成長」「生長」どっち?
成長: 生物の体が大きくなること
栄養 nutrient (肥料 fertilizer, 土 soil) 成長 growth: 光合成で物質貯蔵する植物にとり光合成能力と関与環境要因の研究は古くから数多くなされる
時間に伴うサイズの変化で表現 |
[ 成長率 | 相対成長則 | 成長曲線 ]
成長率 (growth rate)成長 growth ≡ ΔG/Δt, ΔG → 細胞・個体・個体群・群集等一定期間の間に生物tが成長した量 (立木では単位はm/yrが多い) 優勢木: 成長良く、林冠crown上層(林冠層 overstory)を構成する ↔ 下層 understory 劣勢木: 林分平均的成長に比べ樹勢弱く成長遅れたもの → 樹勢衰える → 枯死 絶対成長速度 absolute growth rate, AGR |
相対成長則 (law of allometry)ある部分の成長速度(dp/dt) ∝ 全体(別部分)成長速度(dw/dt)
1/p·dp/dt = h·1/w·dw/dt (両辺積分) 拡張相対成長則生物成長上限 = 上限(pmax)仮定を含めた相対成長則 Ex. 直径(w)-樹高(h)1/p = 1/(H·wh) + 1/pmax__(H, h, pmax: 推定対象変数)
pmax: (潜在的)最大樹高 (w → ∞) → (p = pmax) |
H/D比 = 苗高/根本径 → 健苗の程度、特に地上部のつり合いをみる。70以上 = 枯損の危険 → 60以下に育苗 T/R率 = 地上部重量/地下部重量 → 根系発達程度(地上部と地下部のつり合い) → 値が小さいほど良苗 徒長: 苗陽光不足や窒素肥料過多、根切り不足等により枝葉が伸長し過ぎ、根とのつり合いがとれない苗木 |
[微生物の成長曲線]
成長曲線が備えるべき条件(Shinozaki 1953)
成長曲線N ≡ 成長パラメータ(Ex. 個体数)t ≡ 時間 dN/dt ≡ 個体数増加速度(= 個体群成長) 0) 指数成長exponential growth基本仮説: 資源 = ∞ (≠ 現実) - 生物が獲得する資源量は生物サイズに比例
N = f(t) → dN/dt ∝ N(t), N(t) = 現在のサイズ(= 仮定: 環境圧ゼロ) 1) ロジスティック成長 logistic growth生活空間または資源: 有限 → R0, r: variable with density (単位面積あたりの個体数)実際の個体数は等比級数的に増加し次第に、高密度で増殖が減少停止 = ロジスティック曲線 a) ミチェーリッヒ式 Mitscherlich equationb) 単純ロジスティック式指数成長からロジスティック式の導出 R0 = 1, r = 0 :→ N = K環境収容量 carrying capacity of environment (飽和密度saturation density) ≡ K 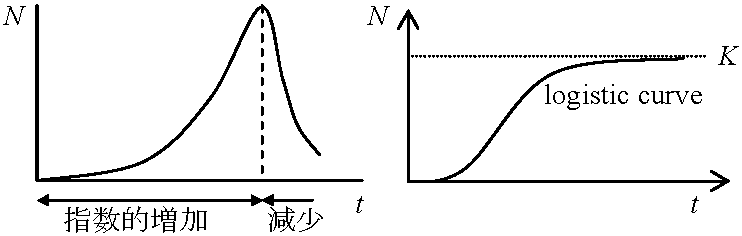 密度 = 0 → R0 = 最大 maximum 密度 = K → R0 = 1, r = 0 N = K(1 + Ke-λt) [単純ロジスティック式] ⇔ 1/N·dN/dt = λ(1 - N/K) N → K ⇒ dx/dt → 0 c) Verhust-Pearlのロジスティック式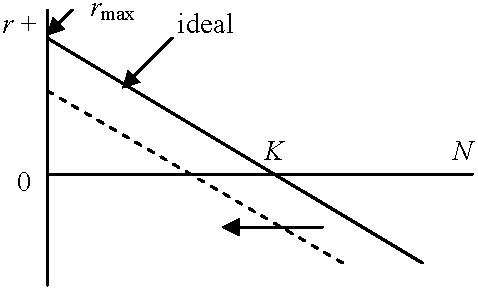 dN/dt = (r - hN)N
dN/dt = (r - hN)N
h: Vershust-Pearl係数 r = b - dbN = b0 - xN dN = d0 + yn
bN: 密度Nの時の出生率 r = bN - dN = 0 → 平衡状態 b0 - xN = d0 + yN b0 - d0 = r = (x + y)N r = (x + y)K x + y = r/K dN/dt = (bN - dN)N = {(b0 - xN) - (d0 + yN)}N = {(b0 - d0) - (x + y)N}N … (1)
b0 - d0 → r = r - hN
(1)式変形: dN/dt = (r - r/K)N = rN{(K - N)/K} 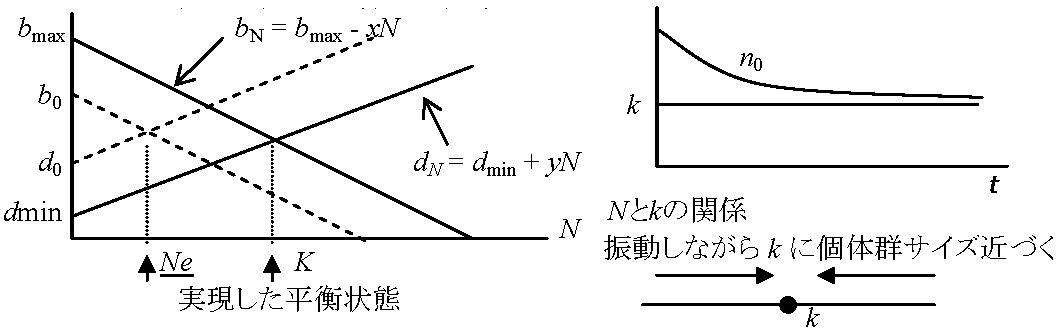 Logistic式仮定
|
Nの上限 = K K = r/h dN/dt = K(1 + ea-rt) Pr.: 個体群が単位時間当たり一定数Aだけ増えると仮定
→ dN/dt = A (Aはある時刻tでその個体群中での出生数と死亡数の差)
増加率rは常に一定 – 齢構成が安定 = 各々の齢での出生率と死亡率が一定 昆虫などの様に世代間が不連続の場合: 世代あたりの純増殖率R0とおいて Nt = N0R0tから求める 世代が連続のときは dN/dt = rn (r: constant) … (1) Nt = N0ert er = λとする (λ: 有限増加率あるいは期間増加率 finite rate of increase) 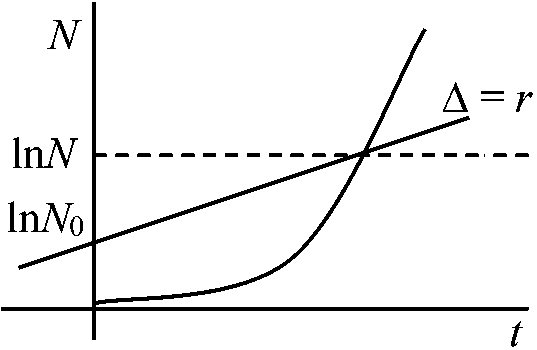
(1)式の積分型 d) ベルタランフィvon Bertalanffy成長式水産学・林学でよく用いるdx/dt = ax2/3 - bx
1つの解釈(右辺): e) ゴンペルツ成長曲線式 Gompertz curvedx/dt = axlog(B/x)(Richards 1959) リチャード関数 Richards equationy = {x∞1-m - (x∞1-m - x01-m)e-K(1-m)t)}(1/1-m)
m = 0 ⇒ von Bertalanffy式 f) ギルピン-アヤラ Gilpin and Ayala (1973)の個体群増殖式dx/dt = rx(1 – (x/K)a)/ag) スミス(Smith 1963)の増殖速度に比例した抵抗を加えた式dx/dt = rx(1 – x/K – bdx/dt)個体群成長率 population growth rate, λ推定法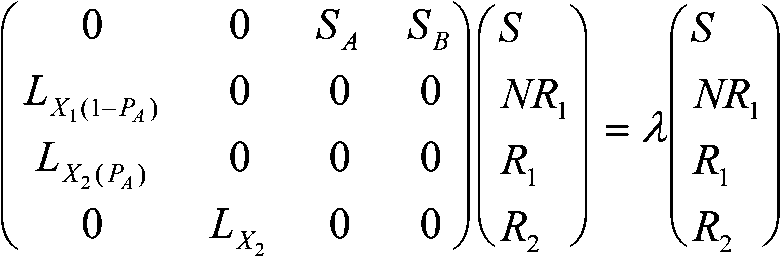
SB: 1年目に付けた平均種子数 (May 1976) カオス caosne+1 = [1 + r(1 - ne/k]nene+1 - ne = r(1 - ne/k)
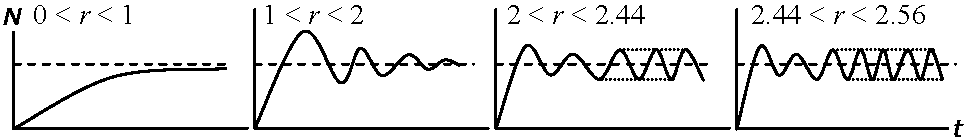
周期2の振動__________周期4 |
[ 樹幹解析 ]
呼吸と光合成呼吸 = 維持呼吸 + 構成呼吸維持呼吸 maintenance respiration: 生命活動維持に使われる呼吸 構成呼吸 construction respireation (= 成長呼吸 growth respiration) 成長過程で組織・器官を構成するのに使われる呼吸 通常は、この両方が同時に進行する1970 McCree: シロツメクサ (C3植物) → 呼吸速度(R)-総光合成速度(P)関係 R = γP + μW (CO2 g/m2/day)
γ: 成長呼吸係数 (0.25/day) ⇒ γP: 構成呼吸量 1978 Kimura: キクイモ → γ = 0.18, μ = 0.07/day 1978 Yokoi (横井): アズキ幼植物(成長は主に使用内貯蔵物質による)
温度 (°C) 20 25 30 Def. 生産力 (生産性, productivity) 単位時間・単位面積当りの生産量 (yield/area/time): 農林学では1年が普通
生態系保全には独立栄養層確保が、肥沃な地域の形成及び保護のため必要 → 生産効率(エネルギー効率)を高める手法開発が具体的課題 Def. 生産量 production: 生産力から時間がなくなる
収量(収穫量) yield: 収穫した分量 回転速度 turnover rate (回転率 turnover ratio) = Pn/B 質量比仮説 mass ratio hypothesis群集内で高現存量種が生態系特性に影響 ↔ 例外多 Def. 総生産量 gross production, Pg = 植物の(光合成による)有機物生産量= Pn + R (呼吸量 respiration, R: 呼吸により失う有機物量) Def. 純生産量 net production, Pn = Pg – R= ΔB + (L + G)
ΔB = B2 - B1: 成長量(種子生産量含む) = 期間1-2での変化 Def. 一次生産量(植物生産量) primary productivity or porduction ≡ Pn = 基礎生産 key production Def. 二次生産量(消費者生産量) = 摂食量 - (呼吸量 + 排泄量)
同化有機物の一部はエネルギー源とし呼吸にまわされCO2や尿素・尿酸等の老廃物として排出される 同化量 = 摂食量 – 不消化排出量 一段高次の栄養段階にある動物の捕食や、病気・事故による死亡で失われる個体も多く、ある栄養段階の消費者の成長量は次のようになる 成長量 = 生産量 – (被食量 + 死亡量) ⇒ エネルギー効率 (Ef) =
[その栄養段階の総生産量 (En)]/[前段階の生産量 (En – 1)] 物質生産 (dry) matter production
独立栄養生物(無機栄養生物) autotroph: 無機物 → 有機物 Ex. 光合成
層 相対 光強度 CO2吸収 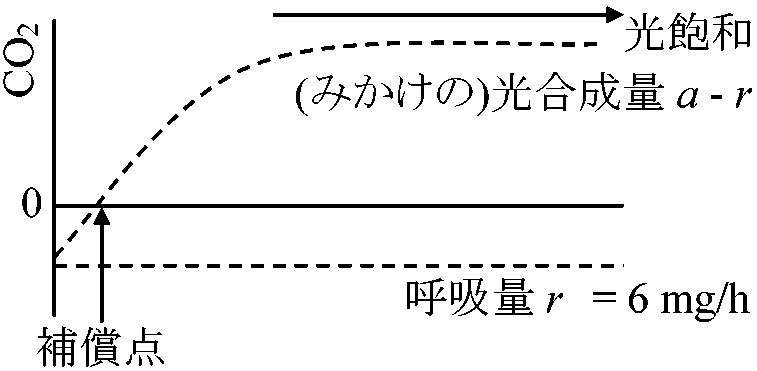
葉100 cm2あたりCO2吸収量 = 8 + 3.2 + 0.6 – 0.6 – 1.0 = 10.2 mg/h 1日では昼間の見かけの光合成量から夜間の呼吸量を引く 10.2 (mg) × 14 (h) – 6 (mg) × 10 (h) = 82.8 mg
1 m2あたり(5層全部で) 82.8 × 102 = 8280 mg = 8.28 g = [F(a – r) – c·R]/F
F: 葉の総面積
a – r: 見かけの光合成量 葉の重なりの密度を調べるのを目的とする。一般の樹木で3-7 |
吸光係数, k: I = I0e-k(n – 1) (≡ ランバート・ベーア式)
I: n番目の層の受ける光の強さ Ex. 葉十分小さく、水平でランダムに分布、透過率ゼロ → k = 1
_____ イネ型____多くの植物__広葉で水平型 S字状カーブ → 成長速度: 山形カーブ
同化(光合成) = 昼間 / 異化(呼吸) = 昼夜両方
光合成量 > 呼吸量 昼____________CO2吸収 (Monsi & Saeki 1953) 門司・佐伯モデル光量鉛直変化 vs 個葉光合成曲線 ⇒ 群集生産速度仮定: 外光(I0)に対する群集内任意高での水平照度(I')の相対値(I'/I0)と群集最上部からその高さまでの葉面積指数(F)間に f(F) = I'/I0 なる関係存在 Fの高さでの光の減衰率: lim(f(F) - f(F + ΔF)/(F - ΔF) = -I0f'(F)
透過光: 葉の光透過率 ≡ m ⇒ ∴ I/I0 = f'(F)/(1 - m) f(F) ≈ I'/I0 = e-kF (実験値) ≡ ランバート・ベーア則
上式は水平葉を過程: 水平面に対してα°で傾く葉 → ∫cos2α1e[(-2F/π){cosα·sin-1(√((1 - u)/u)·cotα) + sinα√(u/(1 - u)·(-cot2α))}]du u = sin2θ, θ = 光入射角
⇒ 自然界ではほぼ成立 (α ≠ 0 → ランバート・ベーア則不成立) p(F) = (bKI0e-kf)/{(1 - m) + kaI0e-kF} 群集光合成数学モデル(門司・佐伯の式): 葉群全体の光合成速度, PP = ∫0Fp(F)dF = (b/ka)·ln[{(1 - m) + KaI0}/{(1 - m) + KaI0e-kF}] … (2) I0: 日変動大(I0(t)で表せれば解決)。あるいは、(1)用い日積算値(I)と日光合成量(p)で計算 ⇒ (2)は総光合成量(総生産量)となる Ps = P - rF
Ps = 日剰余生産速度
⇒ p = rとなるIまでのF - (r/k)·ln[{kI0(b - ar)}/{r(1 - m)] I0十分, k↓ ⇒ Fo↑, Psmax↑ (Fo ≈ Fmax or Fo < Fmax) コジイ・イチイガシ林: a = A/(I'/I0) + B, b = C/(I'/I0) + D ⇒ P = (kCFI0)/{(1 - m) + kAI0} + {D/Bk - CI0/{(1 - m} + kAI0}·
ln[{(1 - m) + kAI0 + KBI0}/{(1 - m) + kAI0 + kBI0·e-kF}] (Boysen Jensen 1923, 門司・佐伯 1950) 物質生産過程物質生産と再生産過程を基盤に、発芽・成長・開花・結実等の時期変化を調べ植物群落の動的性格を示す一年生植物の生産過程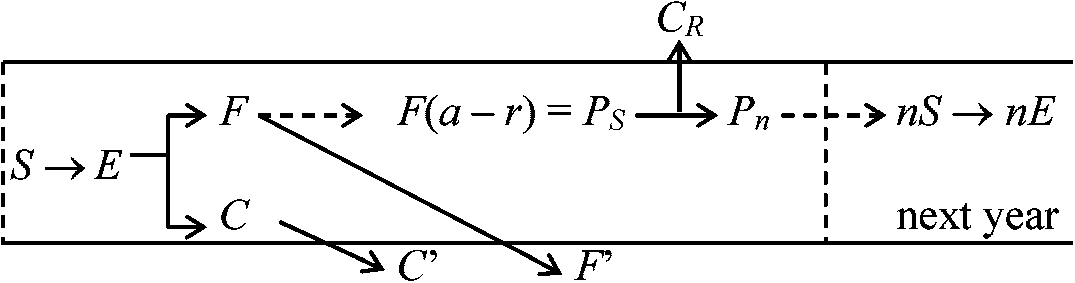
F: 光合成系 C: 非光合成系 多年生植物の生産過程
G: 次年度に残った光合成系の部分 生態系の平衡Def. 生態系内で生体量・種数・個体数が平衡に達した状態一般に、生態系内NPPは増加から減少に転じ、やがてほぼ0 極相状態 → GPP上限 ⇒ GPP ≈ R (平衡状態)
⇒ 純生産量 = 0: 生体量、個体数はもちろん、共存種数さえ増加困難
生態系生産量、呼吸量 → 季節、天候等で変化 P/R > 1 生産的 → 発達 ⇔ P/R < 1 消費的 → 衰退 Ex. P/R > 1 農地(R ≈ 0.5) (g/m2/day)Ex. P/R ≈ 1 沙漠(P, R = 0.2)-海岸(0.5)-湖(1)-沼(6)-草原(10)-森林(50) Ex. P/R < 1 汚水(R = 20) 群集遷移: 初期 = P/R > 1 → 減少 → 極相 ≈ 1 |