(2023年6月16日更新) [ 日本語 | English ]
|
┌───────────────┐
a) 当面の仮説 b) 一般的前提 統計的有意性 vs 生物学的有意性: 統計的有意 = 偶然を越えた差存在 → 生物学的意義があるとは限らない 統計的有意性と生物学的有意性に極端な差ないようなデータ採取必要 統計的仮説 statistical hypothesisと検定手順 test procedure帰無仮説 null hypothesis, H (H0)母集団分布に関する命題 = 差なし(有れば無に帰する仮説) 対立仮説 alternative hypothesis, K (H1)H棄却時に本当に正しいと考えられる仮説 Def. 検出力 (検定力) power (of test): 対立仮説正 →
対立仮説の検定での採択確率, α (Ex. 0.01, 0.05) ⇔
Ex. 両側検定は片側検定より検出力低 検出力関数 power function
仮説 hypothesis
確率化検定関数, P(x) → (0, 1) ↔ 非確率化検定関数 D: 棄却域 critical region ↔ 採択域 acceptance region:T(x1, x2, … xn) ∈ D ≡ reject H → 検定有意 significant α: 有意水準(危険率) significance level (p値 p values):
検定をする → 1つの棄却域Dを定める H正しいが棄却するための誤り (確率αで起りうる) 第二種の誤り(過誤) Type II error (β error, error of the second kind)
H正しくないが棄却しないための誤り 検定する = 1つの棄却域Dを設ける → P{T(X1, X2, … Xn) ≤ D}= α i) 片側検定one-tailed (-sided) test
|
iii)
i) 
ii)
iii) f(x): 仮説Hを正しいと考えた時 → g(x): 真の分布 / 斜線部が第2種の誤りをおかす確率の範囲 外部仮説(事前仮説) = データと独立な仮説↔ 内部仮説(事後仮説) = 標本特性(平均・分散等)から導かれそうな分布仮説 Def. 最強力検定 most powerful test (MP):
H = f(x1, x2, … xn) ↔ K = g(x1, x2, … xn)
D = {(x1, x2, … xn); g(x1, x2, … xn)/f(x1, x2, … xn) ≥ k}
→ ∫D*f(x1, x2)dx1dx2 ≤ α = ∫Df(x1, x2)dx1dx2 → ∫D0*f(x1, x2)dx1dx2 = ∫D0f(x1, x2)dx1dx2
D0*: f(x1, x2) ≥ 1/k·g(x1, x2), ≤ 1/k·∫D0g(x1, x2)dx1dx2 ∴ ∫D*g(x1, x2)dx1dx2 ≤ ∫Dg(x1, x2)dx1dx2: D*がDを越えることはありえない → 最強力検定となる 応用: (x1, x2, … xn)~N(μ, σ02), μ 未知, σ02既知, H: μ = μ0 ↔ K: μ > μ0f(x1, x2, … xn; μ1)/f(x1, x2, … xn; μ0) = Exp[(μ1 – μ0)/s02·Σxi + n·(μ02 – μ12)/2σ02] D = [m ≥ μ0 + zασ0/√n], (1/√2π)·∫zα∞e–x2/2dx = α Ex. α = 0.05, zα = 1.645 → Dはμ1に全く依存せず決まる → μ1 > μ0に関し一様に最強力な検定となる Def. 一様最強力検定 uniformly MP test, UMP
= MPがただ1つに定まる。漸近的にMPと同 (Savage 1956) |
= 母数検定 + 適合度検定
A) 母数検定(母数の検定) parameter test母集団型既知 → H: 母数θがある値をとる → H; θ = θ0I. 1試料 → N(μ, σ2), X1, X2, … Xn~N(μ, σ2)1. 母平均μの検定: μが知りたい → σ2はさしあたり興味なし= 局外母数(撹乱母数) nuisance parameter a) 母分散σ2既知 → 正規分布H: μ = μ0 ↔ 1) K: μ > μ0 (右)片側検定, or 2) K: μ ≠ μ0 両側検定
m, N(μ, σ2) ∋ √n·(m – μ)]/σ (≡ T)~N(0,1) → Dはt = √n·(m – μ0)/σから求まる Ex. 製品 = 不純物 ≤ 4% → 合格工場で200個抜き出し不純物平均値4.2 ± 4.2% (SD)。工場製品は合格? A: H: μ = 4, K: μ > 4
→ t = [√200 × (4.2 – 4)]/1.5 = 1.885 (検定統計量 test statistic) ≤ D0.05 H: μ = μ0 ↔ 1) K: μ > μ0 右片側検定, or 2) K: μ ≠ μ0 両側検定 t値 (t value), t = {√(n – 1)·(m – μ)}/S~t(n – 1) Ex. n = 10 → t(df = 9) → P{T > 1.833} = 0.05, P{T > 2.26} = 0.01D = [1.833, ∞], D = [-∞, -2.26]∪[2.26, ∞] Ex. 薬品を10人の患者に投与 → 平均睡眠時間延長 = 1.24 ± 1.45 (SD)薬は睡眠時間増加効果あるか A. t(10 – 1) = [√(10 – 1)·(1.24 – μ)]/1.45 = 2.57 ∈ DH: μ = 0, K: μ > 0 → reject H = 睡眠時間は増加した 2. 母分散σ2の検定 (μ, 母平均) → σ2-dist (χ2検定): T = T(X1, X2, …, Xn)a) μ既知, N(μ, σ02) → χ02 = Σi=1n(Xi – μ)2/σ02~χ2(n) b) μ未知, N(u, σ02), u = 不偏分散
→ χ02 = Σi=1n(Xi – m)2/σ02 = (n – 1)u/σ02~χ2(n – 1) 1) K: σ2 > σ02 片側検定, or 2) K: σ2 ≠ σ02 両側検定 p = P(χ2 ≥ χ02): p > 0.5 → P = 2 × (1 - p), p < 0.5 → P = 2 × p EX. ある製造ラインで製品10個の重量測定
→ 標本不偏分散4.5。正常では(母)分散2.1。現製造ラインは正常か
χ2(10 – 1) → 標本数: n, 対象属性を持つもの(陽性数)の数r → 標本比率: p = r/n，母比率: π, 母比率の特定値π0 H: π = π0, K: π ≠ π0 → 有意水準αで両側(片側)検定 a) 正規分布: 標本数十分 min[n × π0, n × (1 - π0]] ≥ 5→ z0 = |π – π0|/√{π0(1 – π0)/n}~N(1, 0) b) F分布 (= 2項検定 binomial test)
p ≥ π0 → v1 = 2(n – r + 1), v2 = 2r, F0 = v2(1 – π0)/(v1π0)~F(v1, v2) A.v1 = 2(20 – 2 + 1) = 38，v2 = 2·2 = 4
→ F0 = 4·(1 – 0.03)/(38·0.03) ≈ 3.4035 II. 2試料 → (X1, X2, …, Xn), (Y1, Y2, …, Yn),Xi~N(μ1, σ12), Yi~N(μ2, σ22) 0. 差の標準誤差 standard error of difference, SED (SEd)SED = √{(SD12/n1) + (SD22/n2)} 1. 等分散性の検定 test of homogeneity (homoscedasticity) of variance= 等分散性分析 homogeneity analysis
等分散性: 時間か群間で分散一定 ↔ 不等分散性 heterogeneity → F0 (F値 F values) = σ12/σ22~F(n1 – 1, n2 – 1) 分散一様性検定ルビーン検定 Levene test (ANOVA) ブラウン-フォーサイス検定 (Brown-Forsythe) ハートレイの検定 Hartley's test: Fmax static 回帰の有意性の検定test of regression2. 平均値の差の検定, H: μA = μB → 正規分布(の応用) A. 対応あり → 対比較法 pair-wise comparison
= 対比較(法) (method of) paired comparison
(対応のある2標本でのANOVAと同意になる) Ex. 新薬は従来薬と比べ効果があるか 従来薬特性値: μ = 100, σ = 5, 新薬特性値 (n = 25): μ = 101.5, σ = 4.9 A. H: μ = 100 → H支持 = 新薬は従来薬と効果差なしvs K: μ > 100 → H棄却 = 新薬は改良された b. ウェルチ検定 Welch test: 不等分散t(φ)~|t0 = ~|(E(X) – E(Y)|/√(SX/nX + SY/nY), φ = (SX/nX + SY/nY)2/[(SX/nX)2/(nX - 1)+(SY/nY)2/(nY - 1)] b'. アスピン・ウエルチt検定 Aspin-Welch's t testc. コクランコックスt検定 Chochran-Cox's t test (Cochran's t-test, Cochran's test) d. サイダックt検定 Sidak's t test: 等分散[σ12 = σ22 (値未知で良い)]H: μ1 = μ2 → μ1 – μ2 = 0, K: μ1 ≠ μ2 Ex. 分散未知の場合に平均の差に関し片側検定の棄却域を求めよA. T統計量 T statistics, T
= [(mx – my)/√(1/m + 1/n)]/√[(m12s + ns22)/(m + n – 2)]
s12 = 1/mΣi=1m(Xi – mx)2, s22 = 1/n{Σi=1n(Yi – my)2} A. P{|T| > 2.1} = 0.05, ms12 + ns22 = Σi=1m(Xi – mx)2 + Σi=1n(Yi – my)2 Ex. A{75, 79, 76, 73, 77}, B{74, 70, 75, 76, 71} A. mA = 76, sA2 = 3, mB = 73, sB2 = 28/6
Test: μA = μB, or μA ≠ μB, = 2.1453 ∈ D
df = 6 + 5 - 2 = 9, α = 0.05 → p = 2.262 > 0.05 B) 適合度(性)検定 test of goodness of fitH0: 一特定分布を母集団がとる ⇒ F = F0 → 分布全体に対する検定
その特定分布への当てはまりの良さgoodness of fitを見る 小サンプルだと仮定は否定できない - あらゆる分布が支持される クラメール・フォンミーゼスの適合度検定 Cramer-von Mises test of fit→ nonparametric 適合度指数 goodness of fit index→ 調整済適合度指数 adjusted goodness-of-fit index ゼロデータ問題: 0が余りにも多いと分布型定まらない
平滑化テスト smooth test 1) 分布型適合度検定: χ2検定 (Pearson's) χ2 test (statistic)(X~N(μ, σ2)): 従来の検定Def. 実測度数(観測値 observation or observed value, Obs): ある分布基準(質的)の下でk個のカテゴリーcategoryに分類
カテゴリー: C1, C2, …, Ck → 計 |
Def. 理論度数(期待値 expectation or expected value, Exp)
m1, m2, …, mk → n 母集団確率変数: H; P(X ∈ Ci) = p(p1 + … + pk = λ) → 理論度数 mi = n·pi
χ2 ≡ Σi=1k(fi – mi)2/mi (≠ 確率変数), n ≈ 十分大 → ti値の仮説には全く試料が用いられない: H; p = pi• → mi = n × pi b) パラメータのsヶの母数を標本から推定
→ その推定値により母集団分布仮定されpiを決定 (< 5で使わない) (Cochran 1954, Poole 1974) Ex. 表. メンデルの実験 Mendel's experiment丸・黄 角・黄 丸・緑 角・緑 計 観察値(実測値, Obs) 315 101 108 32 556 遺伝子群 C1(AB) C2(Ab) C3(aB) C4(ab) 理論値(期待値, Exp) 9: 3: 3: 1
H1: p1 = 9/16, p2 = 3/16, p3 = 3/16, p4 = 1/16 m3 = 556 × 3/16 ≈ 104, m4 = 556 × 1/16 ≈ 35 χ2 = (315 – 313)2/313 + (101 – 104)2/104 + (108 – 104)2/104 + (32 – 35)2/35 = 0.510
df = 4 – 1 = 3, χ20.05(3) = 7.815, P{χ2 ≥ 7.815} = 0.05, D = [7.815, ∞] 2) 独立性検定 independence test (≡ χ2検定)(ランダムサンプルで)2変数が母集団で無関係かを調べる分割表(連関表, 4分表, 2 × 2分割表) contingency table (two-by-two frequency table) = 正確(確率)検定(厳密検定, 直接法) (Fisher's) exact test = フィッシャー・イェーツの検定Fisher-Yates test フィッシャーの分類関数の係数 Fisher's classification function coefficients Ex. 性別の運転免許保有率。( )期待値。n = 13
あり なし 計 分類基準 A ○ × 全桝目 all cells: Σ(Obs – Exp)2/Exp = χ02~χ2(df = (行数 – 1) × (列数 – 1) = 1) マクネマー検定 McNemar test: 分割表を従属標本から得た場合のχ2検定
→ 比率検定, χ2 = (b – c)2/(b + c) a/(a + b) = c/(c + d), or a/(a + c) = b/(b + d) → 分類基準A, Bは独立: ad = bc → 独立性の条件 C = (ad – bc)/(ad + bc) → C = 0 独立, C =±1 完全に関連 (-1 ≤ C ≤ 1) Ex. C = (4 × 6 – 2 × 1)/(4 × 6 + 2 × 1) = 0.846 グッドマン・クラスカルのタウτ (Goodman and Kruskal's tau) → χ2検定: χ2 = [(a + b + c + d)/(ad – bc)2]/[(a + b)(c + d)(a + c)(b + d)]χ02 = 3.745 < χ20.05(1) = 3.84 → accept H → 男女免許保有率に有意差は認められない 実際: 全期待値 < 5 → χ2検定不適 → マン・ホイットニーのU検定 一致係数: バイナリ－データ → {(0, 0) + (1, 1)}/総数a. ケンドールの一致係数 Kendall's coefficient of concordance, W
W = χ2/(k·(n – 1)), k: 評価者数, n: 対象数 → グッドマン・クラスカルのλ, Goodman and Kruskal's lambda c. コーエンの一致係数 Cohen's measure of agreement, κ
→ [拡張] 重み付け一致係数weited κ 3) (対数)尤度比検定 (log-)likelihood ratio test, LRT, G-test標本数に応じ有意水準変える頻度 fA, fB, 観測比率 p, q, 期待頻度 f1^, f2^, 期待比率 p^, q^
→ f1 + f2 = f1^ + f2^, p + q = p^ + q^ = 1 H: nCf1p^f1q^f2 = nCf1pf1qf2 → 尤度比 likelihood ratio (L) L = (nCf1p^f1q^f2)/(nCf1p^f1q^f2) = (p/p^)f1·(q/q^)f2 = (f1/f1^)f1·(f2/f2^)f2~χ2α(k – 1), k十分大 対数尤度比 log-likelihood ratio, G
G = 2logL =2(f1ln(f1/f1^) + f2ln(f2/f2^)) Williams修正: k小時の調整, Gadj Gadj = G/(1 + (k2 – 1)/(6n(k – 1))), k: 水準数, n: 標本数 Ex. 表. メンデル実験 →
f1/f1^ = 315/313, f2/f2^ = 101/104, f3/f3^ = 108/104, f4/f4^ = 32/35 → G = 0.5168 < χ20.05(4 – 1): accept H Ex. 表. 性別運転免許保有率
L = 2.214 – 1.230 – 0.993 + 1.999 = 1.990,
粗オッズ: 調整オッズadjusted oddsと混同を避ける時の呼称
処理 - +
= 粗オッズ比 crude odds ratio = {a/(a + c)}/{b/(b + d)} Def. 処理時リスク推定値, π1 = b/(b + d)↔ 非処理時リスク推定値, π2 = a/(a + c) Def. リスク差 (過剰危険 excess risk), RD処理による事象増減を絶対的変化の大きさで表した値 RD = π1 – π2 絶対影響差 absolute risk (reduction), risk difference, ARR ARR = |a/(a + c) – b/(b + d)| 効果発現必要数 number needed to treat, NNT NNT = 1/ARR: 1事象防止に必要な(治療者)数 Def. (4分)点相関係数 (four-fold) point correlation coefficient, φ= phi coefficient, φ = (ad – bc)√(ghij) Mantel-Haenszel (M-H)法複数4分表 → 表併合し検定(一般的方法) → 比率(オッズ比等) = 効果指標 M-H推定: 比率の点(共通オッズ比、共通リスク比等)推定値と信頼区間を求める 交絡因子で層別したクロス表から統合したオッズ比を求める方法 M-H検定: Mantel-Haenszel-χ2値から有意確率を求める 効果指標: 危険 risk → リスク関数 risk function
相対リスク(危険度) relative risk (リスク比 risk ratio), RR → リスク管理 risk management 4) 無相関検定: 標本で得た相関係数大(みかけ相関 spurious correlation)
→ 母集団に必ずしもあてはまらない |
|
分布 = 位置(中央値)とバラツキにより与えられる 位置のずれを検定(ずれの検定 slippage test): H0 = 2つの母集団分布のばらつきが(余り)違わない バラツキの違いを検定: H0 = 2つの母集団分布の位置は(ほぼ)同じ → 散らばりの程度(分布形)比較 2試料無作為化検定法H0 → m1 = m2独立 ↔ 対応 観察値は間隔変数以上、正規分布・等分散の仮定必要ない 1) 独立2試料無作為化検定法2試料の平均値の比較 2) 対応2試料無作為化検定法仮定: 2試料間で個々の観察値に対応ある = 試料間のnは等しい I. 分布位置のずれに敏感な検定順位和法 alternatively a distribution-free test 1. 中央値(メディアン)検定median test2. ムードの(メディアン)検定Mood's W-test (Mood's test of variance)→ 順序尺度以上2母集団のある特性の分布のバラツキの大きさの違い 3. モーゼスの検定Moses test= 尺度差の順位検定H: 実験変数が何人かの被験者に一方向に影響し、残りの被験者には反対方向に影響する 極値の反応を対照controlの反応と比較(外れ値検出にも用いる) この辺整理 A. 独立2群a. 正規スコア検定 normal score test= ファン・デル・ベルデン検定 Van der Waerden's test順序尺度以上 n > 20 H: xa = xb (x: 母代表値) → 位置の差の検定 データに正規性仮定可能 → Wilcoxon検定より検定効率高 小さい方からi番目の標本の正規分布%点, zi
zi = Φ{i/(n + 1)} → S = Σi∈azi b. ウィルコクソン順位和検定 Wilcoxon rank sum test= マンホイットニーU-検定 Mann-Whitney U-test順序(順位)尺度以上 - 順位合計から計算される独立2標本t検定(符号検定の仮定より厳しい)差異(Ex. 同個人の異なる順位付)の大きさに意味 → 符号検定より敏感 → t検定よりType I error増加 H: Ma = Mb (標本母集団中央値) → Wilcoxon static, W
W = Σi=1n1+n2iui 小 → H棄却 c. ワルド・ウォルフォビッツ連検定(ラン検定) Wald-Wolfowitz runs testn = 十分大(小なら補正か使わない)H: 2組の独立標本は同一母集団から得た → K: 2グループは何らかの関わりのある点で異なる 何らかの点(Ex. 中心的傾向、変動性、歪度)で2母集団異なればH棄却 = 広範な種類の対立仮説検定 |
↔ 多くの検定: 2グループ間1特性値の差を扱う d. コロモゴロフ-スミルノフ検定Kolmogorov-Smirnov test, K-S test簡便・強力 = 2標本分布の分散・尖度に敏感Sn1(x), Sn2(x): 実験1, 2からの相対累積度数 D = max|Sn1(x) - Sn2(x)
両側検定: 2標本が同母集団から抽出されたか否か Ex. N ≥ 35, P = 0.05 → Dα = 1.36·√(n1 + n2)/(n1·n2)
片側検定: 標本1が標本2より大きいか否か 小標本で有効(標本サイズある程度大(n > 40) → 標本サイズ不一致でも可)
H: Da = Db (D: 標本の母集団分布) → K-S static e. テューキー簡易検定Tukey’s pocket test (Tukey’s quick test)= non-parametric t-testf. 3角検定triangular test独立2順序尺度変数間系列分析 sequential analysis → triangular sequential samplingB. 対応2群a. 符号検定 sing test (= 2項検定 binomial test)順序 → 必要唯一仮定: 連続分布 (continuous distribtion)→ 分布性質形状仮定不用 H: xA = xB, or xA - xB = 0 → 大きい割合も小さい割合も1/2 n組中r組以上が+になる確率, P P = Σi=rnnCi(1/2)n, one-sided (P = 2Σi=rnnCi(1/2)n, two-sided)
≈ z = {(r ± 0.5) - n/2}/{(√n)/2} z値計算 (z値有意確率 observed significance level of the test計算) b. ウィルコクソン符号順位検定 Wilcoxon signed rank test= matched pair test順序尺度以上 H: xAr = xBr: 対応標本の差をとる → 差の絶対値に順位(0は除く) → 正負それぞれで順位和を合計し、小さい方を検定統計量Tとする
P = P(|z| ≥ z0) II. 分布の散らばりの差に敏感な検定1. アンサリ-ブラッドレイ検定Ansari-radley dispersion test, A-B test仮定: 2つの母集団分布位置は等しい H: sA2 = sB2 → A-B統計量, A
A = Σi=1Niui + Σi=N+12N(2N - i +1)ui = W + Σi=N+12N(2N - i +1)ui 2. カイパーKuiper検定2母集団分布f(x), g(x)の位置は等しい(K-S testの変形)H: 2標本の分布の形は同じ → カイパー統計量, K K = max1 ≤ l ≤ n1+n2Σi=1lSi - min1 ≤ m ≤ n1+n2Σi=1mSi = K1 - K2 3. サベジ検定Savege test仮定: 2母集団分布の散らばりの程度は(大体)等しい - 既知H: f(x) = g(x) → → サベジ統計量, HK HK = {W - E(W)}2/V(W) + {A - E(A)}/V(A) ~ χ2(df = 2) → 仮説支持 |
実験計画法 design of experiments, experimental designDef. 要因: 従属変数に影響しそうな複数独立変数 → 少数要因に絞り他はできる限り統制し少数要因効果検討因子 element: 比較したい特性(n因子実験) 実験計画事前決定事項
三原則完全無作為化法completely randomized design = 1, 2の条件を満たすもの
ブロッキングblocking = 層別抽出法 Ex. 適格基準・除外基準設定、交互作用解析、サブ群解析 設定条件: 対照群 control group
分散分析 (ANOVA)平均値間の有意差検定に分散比較をするのが名前の由来s.s.: 1変量分散分析 (2群 = 2標本t検定と同) s.l.: One-way ANOVA + ANCOVA + MANOVA + general multivariate analysis of variance (GMANOVA) Def. 水準, k: 因子段階を複数に明示したもの Def. サンプルデザイン sampling design
仮定: 測定値xij = 因子主効果 + 誤差効果 xij = μi + eij (i = 1, 2, …, k. j = 1, 2, …, n) = μ 一般平均(母集団平均) + αi 水準効果 + eij 誤差 error
μ = (1/k)·Σi=1kμi, mx = μ + me, me = 1/kΣi=1kei = 1/(kn)Σi=1kΣj=1neij xij = mx + (mxi – mx) + (xij – mxi) ∴ xij – mx = (mxi – mx) + (xij – mxi), Σ(xij – mxi) = 0 Def. 偏差平方和 sum of squared deviation, S S = ΣiΣj(xij – mx)2 = ΣiΣj(mxi – mx)2 + 2ΣiΣj(mxi – mx)(xij – mxi) + Σij(xij – mxi)2 __= nΣi(mxi – mx)2 + ΣiΣj(xij – mxi)2Def. 全体(偏差)平方和, ST ≡ ΣiΣj(xij – mx)2 Def. 処理平方和, SA ≡ nΣi(mxi – mx)2 Def. 誤差平方和, SE ≡ ΣiΣj(xij – mxi)2 Th. 平方和 sum of square の加法定理 (平方和分割 decomposition of sum of squares): ST = SA + SE Th. 平方和自由度の加法定理: fT = kn – 1 = k – 1 + kn = fA + fE 残差平方和自由度, fE
= (偏差総個数) – (偏差間に成り立つ制約条件数)
処理平方和自由度, fA = (因子水準数) – 1
処理平方和期待値 E(SA), 残差平方和期待値 E(SE), 水準間分散期待値 E(VA), 誤差分散期待値 E (VE) = n[Σiαi2 + 2ΣiαiE(mei - me) + E{Σi(mei – me)2}] eij ∈ N(0, σ2), mei ∈ N(0, σ2/n), me ∈ N(0, σ2/kn) Def. 不偏分散 unbiased variance, E(x)(平均平方 mean square, 分散と呼ぶこともある) E(x) = 偏差平方和/自由度
E(mei) = E(Σi(mei – me)2/(k – 1)) = σ2/n
E(mei – me) = me – me = 0
E(SA) = n(k – 1)σA2 + (k – 1)σ2 = (k – 1)(nsA2 + σ2) E(Σi(eij – mei)2/(n – 1)) = E(eijの不偏分散)
E(SE) = E(SE/(k(n – 1)) = σ2
VA = VB → αi = 0, i = 1, 2, …, k → Def. 分散比 variance ratio, F = VA/VE F = (SA/(σ2fA))/(SE/(σ2fE)) = (SA/fA)/(SE/fE) = VA/VE~F(fA, fE)
→ 1) eij: 正規性ある、2) VA, VEは独立 要因 平方和S DF 分散V 分散比F 分散の期待値 因子A SA fA=k-1 VA F=VA/VE σ2+nσA2 誤差E SE fE=k(n-1) VE F(fA/fE)と比較 全体T ST=SA+SE fT=fA+fE Ex. A1, A2, A3, A4の睡眠薬の効果比較 12人を3人ずつ4組に分け、薬を与え睡眠時間を計る ⇒ 一般平均 = バラツカナイ部分 = 総平均 = 15, k = 4, n = 3薬効果 xij = 総平均 + 薬効果によるバラツキ(aj) + 誤差によるバラツキ(eij)
反復 A1 A2 A3 A4 全体 a1 a2 a3 a4 e1 e2 e3 e4
全体(偏差)平方和 = 32 + 22 + (-2)2 + … + (-3)2 = 90 |
乱塊法 (層別無作為配置法) randomized block design (method)ブロック・ランダム化法 block randomization= 交互作用なし二元配置分散分析データ構造模型: xij = μ (一般平均) + ai (処理効果 treatment effect) + bj (ブロック効果) + eij (誤差) 測定値: xij= mx[一般平均] + (xi(A) – x)[処理効果] + (xj(B) - x)[ブロック効果] + (xij – xi(A) – xj(B) + x)[誤差] 因子 factor A: mxi(A) = Ti(A)/r → 第i水準(平均)推定値 Ti(A) = Σj=1rxijブロック block B: mxj(B) = Tj(B)/k → 第j水準(平均)推定値 Ti(A) = Σj=1kxij 全体: mx = T/(kr) → 一般平均μ推定値 T = Σi=1kΣj=1rxij = Σi=1kTi(A) = Σj=1rTj(B) ここで Σi(mxi(A) – mx) = 0, Σj(mxj(B) – mx) = 0,Σj(xij – mxi(A) – mxj(B) + mx) = 0 平方和 ΣiΣj(xij – mx)2
= ΣiΣj{(mxi(A) – mx)2 + (mxj(B) – mx)2 + (xij – mxi(A) – mxj(B) + mx)}2 + ΣiΣj(xij – mxi(A) – mxj(B) + mx)2 Th. 平方和の加法定理: ST = SA + SB + SE全体の平方和: ST = ΣiΣj(xij – mx)2 df = fT = kr – 1 処理平方和: SA = ΣiΣj(mxi(A) – mx)2 = rΣi(mxi(A) – mx)2 df = fA = k – 1 ブロック平方和: SB = ΣiΣj(mxj(B) – mx)2 = kΣj(mxj(B) – mx)2 df = fB = r – 1 残差平方和: SE = ST – SA – SB df = fE = (k – 1)(r – 1) Th. 自由度も加法定理成立:fT = kr – 1 = (k – 1) + (r – 1) + (k – 1)(r – 1) = fA + fB + fE 不偏分散の期待値
E(SA) = (k – 1)(σ2 + rσA2),
E(SB) = (r – 1)(σ2 + kσB2)
(Σi=1kαi = 0, Σj=1rβj = 0, eij ∈ N(0, σ2), ブロック配置 法block design全体は、それぞれ因子Aの第i水準aiとブロック因子Bの第j水準bjの平均
HA: 処理間に差ない → αi = 0, i = 1, 2, …, k → σA2 = 0 要因 平方和 S df 不偏分散 V 分散比 F 分散の期待値 処理 A SA fA = k - 1 VA VA/VE σ2 + nσA2 ブロック B SB fB = k(n - 1) VB VB/VE σ2 + nσB2 残差 E SE fE = (k - 1)(r - 1) VE σ2 全体 T ST = SA + SB + SE fT = fA + fB + fE 要因実験(計画) factor analysis要因効果を評価できる実験計画交絡 confound: 処理反応を歪める、見かけ上の関連を生じさせる第3の因子(撹乱因子 nuisance factor)
処理 treatment → 反応 response → 交絡 = 年齢 - 年功序列社会因子: 血圧・給料は年齢と共に上昇 交絡除去方法: 実験段階 = 完全無作為化法、解析段階 = 調整解析 adjusted analysis交互作用 interactionある因子が他の因子と互いに相乗的(相殺的)に効果を及ぼすこと
→ 判断は第2種の過誤を避けるため、経験的には水準20%程度で行う(理論未確立) n2要因実験2因子A, Bの要因(= n2)効果を調べる実験計画22要因実験主効果 main effect: 交互作用を取り去った効果要因効果: 主効果 + 交互作用 表. 繰返し(交互作用)のない要因実験
要因: E(S), df, E(V)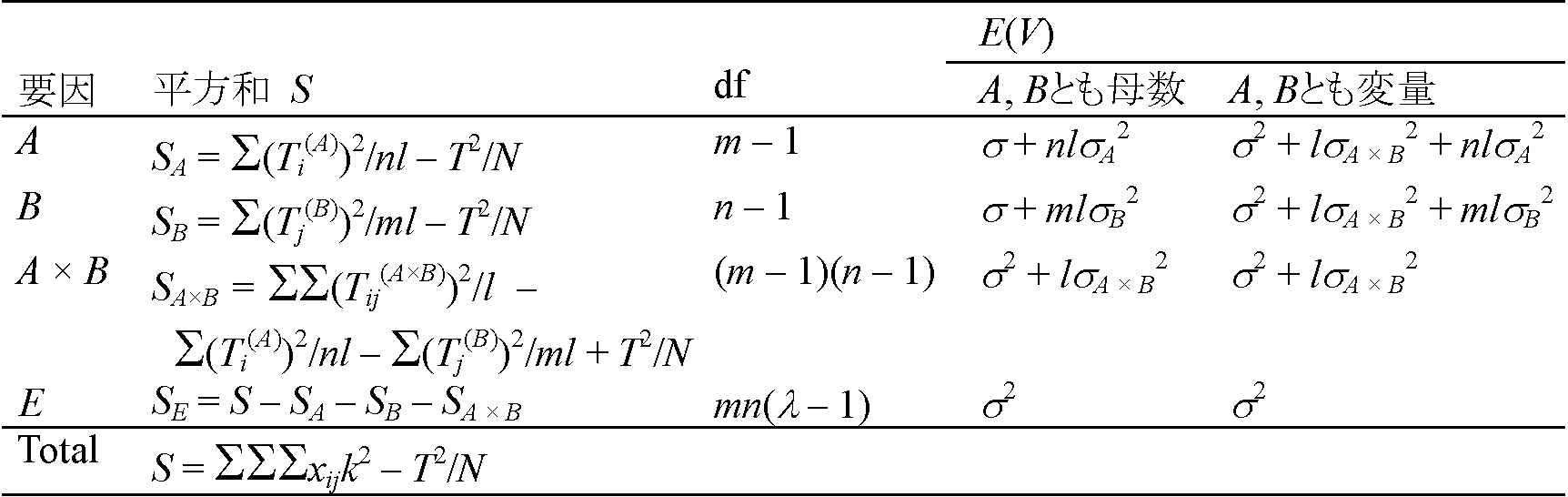 
a) B1 B2 B3 方格実験回数を減らす方法 – 因子水準は全て同じa) ラテン方格(方陣) Latin square: 3水準3因子実験: 9回の実験 → 2元配置では33回実験必要 b) グレコ･ラテン方格(方陣) (オイラー方格): 4水準4因子実験: 16回の実験 → 2元配置では44回実験必要 c) 直交表(直交配列表) table of orthogonal arrays: 方格拡張→ 直交配列を一覧表に整理したもの ラテン方格 → グレコ・ラテン方格
→ k水準の因子ではk - 1個の因子までを二元配置に組み込めk = ps → 実験計画法で利用される直交配列(配置)とよばれる配置のもと 多因子要因実験(多要因実験) factorial experiment多元配置 factorial design枝分れ(配置)分散分析, 巣篭もり型分散分析 nested (designs) ANOVA |
|
分布によらない検定 distribution-free test パラメトリック検定: 仮定 = 分布(多くは正規分布) + 等分散性 ノンパラメトリック検定: 母集団分布に関わらず適用できる検定手法群の総称 → 分布型仮定ないが等分散仮定 順位相関 rank correlation同順位(タイ)tie (tied rank)の調整(Siegel & Castellan 1988)スピアマンの順位相関 Spearman's rank correlation (r or rs)Spearman's rank correlation coefficient, r = 1 – 6/(n3 – n)Σi=1n(xi – yi)2
n個の対応データを順位付け並べた順位対から計算される相関係数 r = (sx + sy + sxy)/(2sxsy) = [2(n2 – 1)/12 – sxy2]/[2(n2 – 1)/12] = 1 – (6xy2)/(n2 – 1)
sxy2 = 1/n·Σi=1n{(xi – mx) – (yi – my)}, mx = my sxy2 = 1/nΣi=1n{(xi – yi) – (mx – my)}2 = 1/nΣi=1n{(xi – mx) – (y – my)}2 sxy = sx2 – 2sxy + sy2, (m(x – y) = 1/nΣi=1n(xi – yi) = mx – my)
= 1/nΣi=1n(xi – mx)2 + 1/nΣi=1n(yi – my)2 – 2/n(xi – mx)(yi – my)
測定値 1, 2, 3, …, n, mx = (n + 1)/2 (∵ 1/nΣi=1n{(n + 1)/2 – i}2 = 1/nΣi=1nxi2 – mx2)
= 1/6·(n + 1)(2n + 1) - (n + 1)2/4 Ex. {x: 1, 2, … n}, {y: n, n – 1, … 1} → r = -1 r = 1 – 6/{n(n2 – 1)}·Σi=1n(xi – yi)2 2. ケンドールの順位相関 Kendall's rank correlation, τKendall's rank correlation coeffcient, τxiに順位 → yiをxiの順に並べる
→ 各iでyi < yj (j > i)となる個数をPi, yi > yjとなる個数をQi 2'. ソマーズの関連指数 Somers's index of association, dSomers's d → τに関連した非対称指数 |
3. グッドマン・クラスカルのγ Goodman and Kruskal's γ4. サイルの検定 Theil's slope coefficient testimcomplete method5. フィッシャー・イェーツ・テリー・ヘフディングの検定 FYTH test= Fisher-Yates-Terry-Hoeffding test2標本順位尺度 6. コーナーテスト(片すみ検定) corner testオルムステッド・テューキー検定 Olmstead-Tukey's test: Olmstead-Tukey corner test of association 差 differenceI. 分布位置のずれに敏感な検定順位和法 alternatively a distribution-free test1. 中央値(メディアン)検定 median test前提 → f(x), g(x)分布形は等しい(サンプルサイズ大 → 検定効率低)
各変数に基づく観測値順位付け(順序尺度)と、変数間差順位付け尺度(順序距離尺度) (Coombs 1950) x(1) ≤ … ≤ x(r) ≤ x(r+1) ≤ x(r+2) ≤ … ≤ x(2r), (x(r) + x(r+1))/2 = xme n = odd →
x(1) ≤ … ≤ x(r) ≤ x(r+1) ≤ x(r+2) ≤ … ≤ x(2r+1), x(r+1) = xme
2標本集団 f(x) = (x1, x2, … xn1), g(x) = (y1, y2, …, yn2)
Si, ui = 1, z(i) ∈ {x1, x2, …, xn1}. Si = –1, or 2. ムードの(メディアン)検定 Mood's W-test3. モーゼスの検定 Moses test今後の課題
|
等分散性成り立たないか標本数が異なる時に頑健
A. 変数間対応関係あり1. コクランのQ検定 Cochran's Q test条件: 名義尺度変数 → 処理間の比率の差を検定(拡張マクネマー検定)2. フリードマン分散分析Friedman's ANOVA ()= フリードマン検定 Friedman's test分布の平均の違いを検出 ↔ 分布形は見ない B. 変数間対応関係なし(独立)1. χ²検定 (χ²-test)名義尺度 |
2. クルスカル-ウォリス検定 (Kruskal-Wallis (ANOVA by rank) test)= K-W ANOVA, H-test, or non-parametric ANOVAH: Amed/dist = Bmed/dist - 解釈: 順位以外はparametric ANOVAと同 3. ヨンキー・タプストラ検定 Jonckheere-Terpstra test群間に順位があればK-W検定より有力H: m1 ≤ m2 ≤ … ≤ mn → 群標本平均に順位 4. (拡張)メディアン検定 median test分割表からの計算で組み立て (K-W ANOVA簡易版)
H: 全標本は同じ中央値を持つ母集団 - 各標本全ケースの50%が共通中央値の上(下)に入る |
|
1実験で多数(2以上)比較を行なうとき、実験全体で第1種の過誤を有意水準以下に制御する統計手法の総称 → 多群間比較に2群間比較方を繰返し用いることはできない
2群比較___処理群___多重比較 [ABCD群: 同じ母集団に属す]
→ A-B, -C, -D全て有意となる可能性高 = 過誤を3回犯す 全て有意差が出ない確率 = (1 - 0.05)3 ⇔ 逆に有意差が出る確率は1 - (1 - 0.05)3 = 0.142 多重性問題対処法1. 検定数減らす: 主要評価項目設定サブ群解析: 層別効果推定、交互作用解析に重点。サブ群毎検定結果は参考程度とすべき 2. 検定優先順位をつける → 上位検定で有意さなければ下位検定不用3. 分散分析(有意水準制御) → 多重比較法使用
包括帰無仮説 overall null hypothesis: A = B = C 対毎の検出力 per-pair power Type I familywise error rate (TI FEW): 各ファミリーの有意水準 → 正しい帰無仮説のうち少なくとも1 つが誤って棄却される確率 保守的 conservative: TI FWEが有意水準よりも小さい ↔ TI FWE > 有意水準 → 検定は多重比較法として不適切 [重要] H{AB, BC, CA}, H{AB, AC} → 多重比較法決定 = 部分帰無仮説族決定 Ex. 経時測定データ: 経時型分散分析 "群 × 時点" 交互作用有意 → 時点ごと群間比較 多重比較に見られる3つの過誤
スチューデント化された範囲統計量 studentized range statistic, q多重比較でよく使用 → スチューデント化された範囲 studentized range外れ値検出に使われる (Cp. t検定 → t分布) スチューデント化 studentization: z = (x - μ)/σ
z: (Student化した)標準化得点 多重比較法多数存在 → 理論未確立 → 明らかに誤った方法以外はどれが正しいとは言えないのが現状A) パラメトリック法 (1)正規性・等分散性・(独立性)仮定満たすa. Tukey family全群間同時比較(Tukey 1953) a1. Tukey's test= honestly significant difference test, HSD, Tukeyのa法, Tuekyのq検定)条件: 群間標本数同じ → 各群母分散同じ。検出力高(= 有意差出易い) H0(i, j): μi = μj → F = {H(1, 2), H(1, 3), …, H(1, n), H(2, 3), …, H(n – 1, n)} 水準数 = n, 反復数 = k群内平均 = 算術平均 誤差分散の自由度 f = 各群の(反復数 – 1)の総和,
fR(A) = Σi=1n(ki – 1) = Σi=1nki – n Si = Σj=1kixij2 – (Σj=1kixij)2/ki 誤差の平方和, SR(A) = Σi=1nSi誤差分散, MS = SR(A)/fR(A) → ANOVA実行してれば計算済み 誤差分散の平方根, s = √(MS) 標準誤差, Sxavg = √(MS/k) = s/√k Q-value = Q(n, f,; α). α, 棄却率 D-value, Dα = Q(n, f,; α) × Sxavg → |μc – μr| > D → reject H0
群 (データ): 合計, 平均, 二乗和 SR(A) = (7555 – 2292/7) + (7447 – 2272/7) + (5198 – 1902/7) + (3912 – 1642/7) = 259.71
平均 A B C s = 3.29 → Sxavg = 3.29/√7 = 1.24 Q(4, 24; 0.05) = 3.9013, Q(4, 24; 0.01) = 4.9068 → D0.05 = 1.24 × 3.9013 = 4.837, D0.01 = 1.24 × 4.9068 = 7.084 a2. Tukey-Kramer test (修正HSD test)群間データ数不一致可(標本数に開きがある時使用)。検出力高Tukey's testで群内平均を調和平均で求めることで、異なる標本数に対応したもの a3. Tukeyのb法= wholly siginificant difference test, WSD testa4. Tukey-Welsh testa5. Spjotvoll-Stoline検定群間データ数不一致用に補正されたテューキーのHSD検定 (Spjotvoll & Stoline 1973)b. Dunnett's test逐次棄却型検定法対照群-実験群 experimental group (多群)間対比較 [群間データ数不一致可] → 順位検定 H0: mc = mr1, mc = mr2, …, mc = mri, …, mc = mrp,k = 1 (control) + p (references) fR(A) = Σi=1k(ni – 1) = Σi=1kni - kSi = Σj=1nixij2 – (Σj=1nxij)2/ni SR(A) = Σi=1kSi MS = SR(A)/fR(A) t1i = (x1avg – xiavg)/√{MS × (1/n1 + 1/ni)} |
Case a) 実験群数同じ ρ = n2/(n2 + n1) Case b) 実験群数異なる
i) λi1 = ni/(ni + n1), i = 2, 3, …, p
群Ai (Mi): 総和、二乗和、平均 SR(A) = 724 – 842/10 + 715 – 752/8 + 980 – 882/8 + 1139 – 952/8
= 53.15 t12 = (8.4 – 9.375)/√{1.771 × (1/10 + 1/8)} = -1.545, t13 = -4.119, t14 = -5.505 ρ = 8/(8 + 10) = 0.44 →d(4, 30, 0.44; 0.05) = 2.485, d(4, 30, 0.44; 0.01) = 3.161 t13, t14 → reject H0b1. ウィリアムズ検定 Williams testDunnett's testに似るが順位想定できる群間に単調性(順位)想定(用量相関) = 片側検定 → 検定結果に群間順序が反映される Ex. 温度: 高 > 中 > 低 → 3群順位づけ(経時的測定データに適応困難) c. ホッホベルグのGT2 (Hochberg's GT2d. ペリ検定 Peritz検定e. シェッフェ検定Scheffe's test全群間比較(多群間中特定群間比較不可) (Scheffe 1953)線型対比 linear contrast 厳しく有意差を求める = Dunnett testと比較し過度に保守的 (Winer 1971) f. ガブリエルの1対比較検定 Gabriel's pairwise comparison testg. ホテリングのT2, Hotelling's T2B) パラメトリック法(2)正規分布に従うが等分散性仮定できないa. ガイムズ・パウエル検定 Games-Howell pairwise comparison test= G-H test (Games & Howell 1976)→ Tukey's testの拡張 Welch統計量 b. ダネットのC (Dunnett's C)ダネットのT3 (Dunnett's T3): Cよりも標本数が少ないときに向く標本サイズが異なる群間比較には不向き c. タムハーン Tamhane法Welth統計量を使う (Tamhane 1977, 1979)タムハーンのT2 (Tamhane's T2) C) ノンパラメトリック検定母集団正規性・等分散仮定しない (パラに対するノンパラは全てある!)小標本(n < 10) → ノンパラ多重比較すべきでない a. スチール順位和検定 Steel's test順位検定 = nonparametic Dunnett's testU-testとほぼ同様な検出力 b. スチール・ドゥワス法 Steel-Dwass test= nonparametric Tukey's test順位を用いた多重比較 (overall null hypothesis test)
H0: M1 = M2 = … = Mi = … = Mn c. ノンパラメトリック Tukey-Kramer検定= Turkey-Kramer's HSD testd. シャーリー・ウイリアムズ検定 Shirley-Williams test= nonparametric Williams teste. Brown-Forsythe testBF test (Brown and Forsythe 1974)Scheffe test修正 → Scheffe tesより不等分散性に頑健 対比較ではGames-Howell法やTamhane法の方が高検出力 → 状況により使い分け必要 f. ヨンキーの傾向検定 Jonckheere test用量相関性(トレンド)の検定 (Joncckheere 1954)3群以上の場合の順位による検定 g. ボンフェローニ検定 Bonferroni test= ボンフェローニ多重比較 Bonferroni's multiple comparison比較回数倍だけ危険率を厳しくする(Wallenstein et al. 1980) Ex. α, n回比較 → α/n%点を用いる (ボーンフェローニ修正 Bonferroni correction) 標準誤差は比較2群データから計算するのでなくn群全体から計算した(プールした)標準誤差≥ 5群で用いない(検出力極端に落ちる) Sequential Bonferroni: 高検出力, α ≤ α/(1 + k – i), i: i番目の比較 → Type II error増える Bonferroni法: ボンフェローニ不等式Bonferroni's inequalityに基づくステップワイズ多重比較論文作成時: 方法のタイプと何群中で何回比較がなされたかを明示 Dunnett型/Scheffe型比較でき多群中特定組合せ比較も可能D) ステップダウン法(下降手順) stepdown method↔ ステップアップ法(上昇手順) stepup methodアルゴリズム: 1帰無仮説を検定 → 結果を元に終了を含む次ステップを選択 → 仮説の階層性hierarchy – ファミリーfamily Ryan-Einot-Gabriel-Welsch's F (R-E-G-W F)Ryan-Einot-Gabriel-Welsch's Q (R-E-G-W Q) Dunnettの逐次棄却型検定法 Closed testing procedure 多重比較不適切方法全てTI FEWを有意水準以下に抑えられないのが理由制限付最小有意差検定 (= Fisher's PLSD or LSD, protected least significant differendce method)
最小有意差 least-significant difference (LSD): 4群以上の差の比較には適用できない(= 3群のみ) Type I error増加を相関行列元に最小限プロテクション → t検定と原理同 = 多重比較使用不適 Newman-Keuls test (Student-Newman-Keuls test, S-N-K test)各処理水準平均値を大きさ順に並べターキー法を逐次的に行う ダンカン(多範囲)検定 Duncan's (multiple range) test→ 改変: Waller-Duncan's t-test: やはり不適切 逐次的全群間対比較 = t検定と似た性質 → 全体有意水準が名義水準を越えるため使用しない |
[ 序列化 ]
多変量: 変量数 ≥ 3 → 多次元変量間関係を分析
分析目標全個体を通し(母集団)変数間の平均的関係を示す= 各変数のある意味での重要性等評価 = 平均的変数間関係と共に、個体間差(個体群間差)を表わす 多次元データ統計分析法共通部分: 全統計分析で検討すべき数量化理論 quantification method質的変数カテゴリに数量与えた多次元的解析(日本特有) (林 1993)質的(定性的)データ(= 名義尺度 + 序数尺度)の数量的取り扱い理論 質的データ → 数量把握時に独自の問題 → 解決のため各種分析法提案 数量化法異質性因子 heterogeneity factor外的基準 outside variable (external criterion = 予測(説明, 従属)変数 predictor variable (慣例でこう呼ぶ)
外的基準ない → データ分類を目指す Ex. III, IV類 数量化I類 quantification method I連続変数から従属変数予測 = ダミー変数dummy variableによる重)回帰分析y = a1x1 + a2x2 + … + anxn + ε
x1 … xn: 説明変数(アイテムitem） 数量化II類カテゴリーデータを説明変数とし群判別 = ダミー変数を用いた判別分析数量化III類= 双対尺度法 dual scaling, 対応分析カテゴリーデータに基づきケースと変数をまとめる = ダミー変数による主成分分析 → 使用変数が間隔尺度以上 = 主成分分析 数量化IV類類似度行列から対象二次元配置求める - 任意基準による類似度行列使用(類似度行列は非対称行列可)。類似方法に主座標分析プロフィールデータを分析対象とした他数量化と異なり、アイテムiとjの親近性からアイテム間関連分析を行う - 非多次元尺度構成法に対応する分析と考えてよい |
表6.2 多変量解析の分類。* 判別分析 = 名義尺度が説明変数、計量尺度である多変数が目的変数(基準変数)とする方が妥当だが従来の分類に従う
手法名 基準変数 説明変数 潜在変数 尺度 名義 計量 名義 計量 名義 計量 重回帰分析 - 1 - 多数 - - 共分散分析 - 1 多数 多数 - - 分散分析 - 1 多数 - - - 数量化I類 - 1 多数 - - - 多変量回帰分析 - 多数 - 多数 - - 正準相関分析 - 多数 - 多数 - - (線形)判別分析 1(2分類)* - - 多数 - - 重判別分析 1(多分類)* - - 多数 - - ロジスティック 1(2分類) - - 多数 - - 回帰分析 多項ロジスティ 1 (多分類) - - 多数 - - ック回帰分析 数量化II類 多数 - 1(多分類) - - - 主成分分析 - - - 多数 - - 数量化III類 - - 多数 - - - 因子分析 - 多数 - - - 多数 クラスタ-分析 - 多数 - - 多数 - 数量化IV類 多数 - - - 多数 - 潜在構造分析 多数 - - - 多数 - 多変量分散分析 multivariate analysis of variance, MANOVA群間比較実験計画Ex. 複数従属変数(各教科成績)が複数教科書の違いに影響を受けるか 誤差分散/共分散行列: 効果による分散/共分散行列 – 比 → 多変量F値(Wilks's λ)従属変数間に関係あれば、分析上考慮必要で分散比の代わりに分散共分散比を用いる 2従属変数が同測定値 → 情報加わらないが、相関関係あっても異なる2測定値なら新情報を得られる Ex. 全体有意差 (Ex. 教科書効果)検出 → 数学、物理、双方同時に関係する効果確認 主効果・交互作用効果に対する多変量検定で有意差得た後、各単一変数に対し分散分析(F検定)利用し各変数に対する効果を確かめるやり方が一般的共分散比 covariance ratio ステップダウンstepdown MANOVA (ロイ・バークマンステップダウンF検定 Roy-Bargman stepdown F test) |
|
複数従属変数回帰分析と分散分析を1以上の因子変数か共変量を使い実行 因子変数: Ex. 従属変数平均値が各群内で同じかを検定するためケース群を定義する独立変数 共変量 coariate: 実験計画では連続型因子を指しSEを小さくし実験感受性を高めるため使用
→ 因子変数から母集団を群分割
因子同士交互作用と因子毎効果の両方を検定 + 共変量効果や共変量と因子の交互作用
フィライのトレース Pillai's trace: 多変量有意差検定の1種 = 0: 群平均に差ある ↔ = 1: 群平均に差ない(全平均が同一なら1) ホテリングHotelling's (ローレイ・ホテリング Lawley-Hotelling)トレース trace 固有値合計に基づく有意差についての多変量検定
Roy最大根Roy's largest root |
平方和 sum of squares の型タイプI, type I (階層的分割法): モデル中で先行する項に対してだけ調整タイプII, type II: タイプIII, type III: 一般的。計画中にある効果の平方和を、その計画を含まないその他の効果、またはそうした効果に対して直交的な効果を対象に調整した平方和を計算 タイプIV, type IV 平方和積和(SSCP)行列モデル効果による平方和と誤差平方和1変量分析 → スカラー形式 → 多変量分析 → 行列形式 残差平方和積和行列(残差SSCP行列)
a) 残差SSCP行列を残差のDFで割った残差分散共分散行列
2種類の比率の押出と量が2種類違う添加物を試し、押出率と添加物の量それぞれ3属性測定 |
[ 多次元尺度構成法 ]
因子モデル factor model固定(因子)モデル fixed model (母数モデル parametric model), FM: I型グループ間差 → 処理効果による = 固定因子 → 固定因子用いる 反復測定repeated measuresによる分散分析(rm-ANOVA) 比較群間は「等分散か無相関」という分散分析前提条件崩れる → Type I error → [補正] Ex. Greenhouse-Geisser correction: DFにε係数(< 1)をかけ自由度小さくする 変量(因子)モデル randam (effect) model, RM: II型 → 変量因子用いる = nested ANOVA混合(因子)モデル mixed model = FM + RM → 時に優れる
時間的/空間的自己相関存在
→ 経時データ ⊂ 反復測定データ 非有意 → ANOVA分割法 有意 → εによる修正ANOVA 高度に有意 → MANOVA 経時測定データ分析多重比較を含む0. 避けるべきもの: 非球面誤差 → 古典的方法不可 1. 古典的方法
反復測定ANOVAとMANOVA 因子分析合成変数に関し全個体平均推定量から各個体標本値分散最大化→ その種の合成変数個数最小限に押さえ標本データ全体の持つ情報を表現 → 採択少数合成変数で標本データ全体を説明時の"誤差"が最小となる。誤差は多変量間の平均的関係を推定し誤差本来の意味を持つがズレが全個体平均からの個体標本値の偏差量であることも意味がある 目標: PCAに似るがm次元標本データを低次元(mより小)新座標軸系で表現 モデル仮定: "因子factor"という表面に出た少数変数の線形結合で説明可
因子負荷量 factor lading: 因子と項目の相関係数 複数の変数の分散を共通に説明する潜在的変数 Def. 特殊性 specificity: 個々の観測変数そのものだけに起因する分散特殊因子(独自因子) specific factor: 各変数固有の分散 = 誤差項 ↔ 共通因子 Def. 独自性 uniqueness = 特殊因子分散 + 誤差分散直交解: 共通因子と特殊因子は直交 = 相関0
特殊因子はそれぞれ直交 手順1. 因子数決定(= モデル決定)
主因子法(主因子分析) principal factor analysis, PFA: 因子中から因子負荷量が最も高くなる因子決定手法
|
3. 因子軸回転と因子の意味の解釈
因子軸回転基準必要 → 回転法の違い = 回転基準の違い
斜交回転 oblique rotation
エカマックス回転 equamax rotation アンダーソン・ルビン法 Anderson-Rubin's method: 因子得点推定法 標本妥当性= 等分散性 → 偏相関係数を見るバートレット検定 Bartlett’s test (バートレットの球面性検定 Bartlett's test of sphericity) 群間の分散の均一性検定 [実はt検定, ANOVAは分散均一性仮定 → 本来は事前にBartlett's test必要]
複数群が共通因子有する → 他変数の線形効果除去時に変数同士の偏相関係数↓ 正規分布からの逸脱に敏感 → 正規分布に従わない標本では分散均一性より非正規性を検出する傾向 正規分布に従わない(と想定される)場合 → 感度低いルベーン検定Levene test好ましい
H0: σi2 = σj2 (i ≠ j) → H1: いずれかの母分散異なる コクランのC (Cochran's C): 有意 = 不等分散性あり → ANOVA等不適 モークリーの球面性検定Mauchly's test of sphericity: 反復測定球面性ないときのdf調整法, ε
ホイン・フェルトのε, Huynh-Feldt epsilon
因子分析の標本妥当性測度 = 観測相関係数/偏相関係数 → 基準値1に近いほうが変数あてはまりよい
正規性仮定に非依存 (SPSS採用) |
(共分散分析とは全く別!!!)
|
因子分析 + 重回帰分析 潜在変数間関係調べる検証的方法 ≈ (潜在変数)構造方程式モデル (SEM/LV)
回帰分析: 仮説存在可だが、観測変数を分析対象 ≠ 共分散構造分析 リズレルLISREL vs エイモスAmos 多重指標(型)モデル multiple indicator multiple cause model = ミミックモデル MIMIC model パス分析(解析) path analysis複数の重回帰分析を組合わせる → 間接効果推定
順序反応 ordered response →
X → [ r ] → Y 間接効果 indrect effect ↔ 直接効果 direct effect
X → [ r ] → Y 構造方程式モデル (SEM)= 共分散構造分析 (Bock & Bargmann 1966)重回帰分析、因子分析、パス解析等の機能を併せ持つ統合手法(つまり無謀) 潜在変数 latent variable: 直接観測できない変数 観測変数 observed variable との間の因果関係から推定
開発初期: 連続型で構造方程式は線形 ⇒ 拡張 R (lavaan package): 構造方程式モデル |
因果分析 causal analysisEx. グラフィカルモデリング graphical modeling
因果係数 causal coefficient システムダイナミクス ☛ system dynamics, SDフィードバック有するシステムでの変化を推定
フィードバック: X → Y (因果関係) → X → … ⊃ オペレーションズリサーチ (OR)、意思決定論、情報理論等 潜在特性モデル (項目反応モデル item response model)潜在変数 latent variable: 概念的・仮説的変数で直接測定不可能Ex. 個性、意識、嗜好 ↔ 顕在(観測)変数 = 潜在変量latent variate (因子): 潜在的に影響を与えることになる要素
tetrachoric correlation (= binary ratings) |
|
新たな観測データが属するクラスを判別
Ex. トマトは果物か野菜か
Ex. 教師データ = モデル内: 従属変数(基準変数 criterion variable)予測に利用される変数参照時 教師つき学習 supervised learning: 教師データを用いた判別
↔ 教師なし学習 = モデル外: モデルに含まれない = 利用されない変数参照時 2値判別1) 線形判別関数(式) linear discriminant function (equation)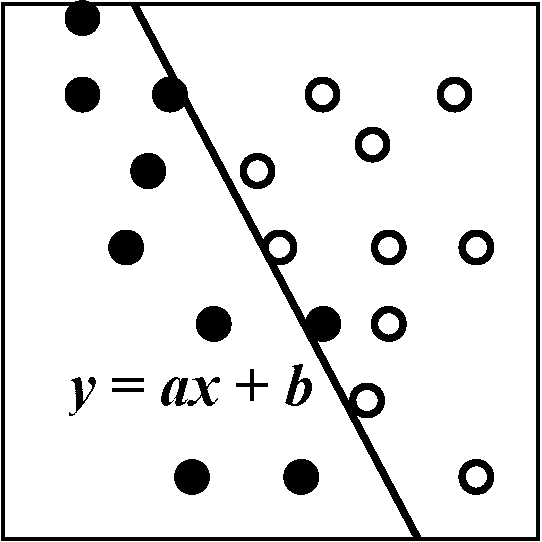
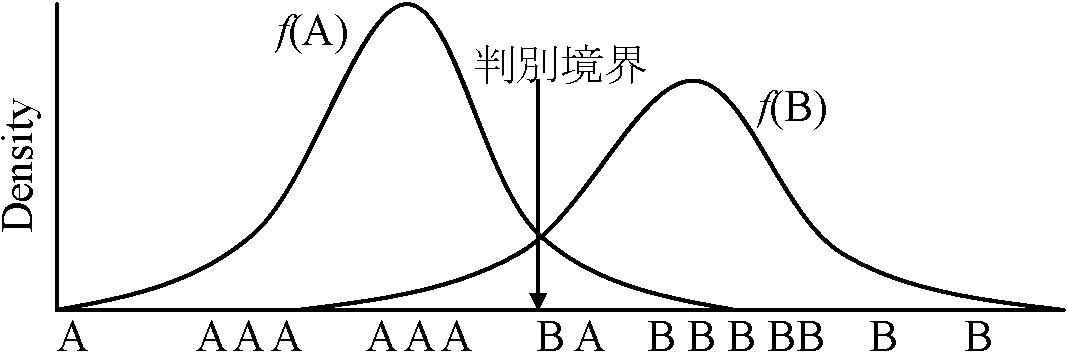 → 判別境界: y = ax + b 判別基準a) 各属性の平均の中間点 → 各分布の分散は同じ(非現実的)b) マハラノビス距離, D2 = (x – μ)2/σ2 i) σ12 = σ22 → D22 – D12 = (x – μ2)2/σ2 - (x – μ1)2/σ2
= {2(μ1 – μ2)/σ2}·(x – {μ1 + μ2}/2)
= (1/σ1σ2){σ22(x – μ2)2 – σ12(x – μ1)2} |
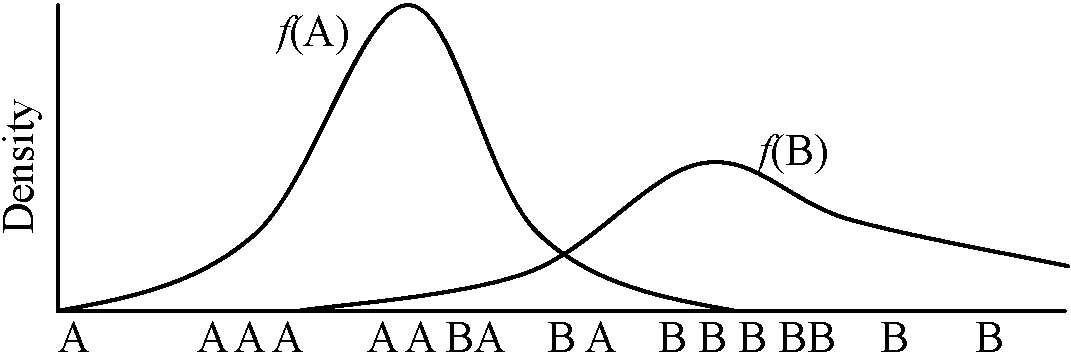
 → n次に拡張: マハラノビス距離をn次に拡張 多値判別 (通常の判別分析)∃x ∈ Ci (class i) → P(Ci = i|x),Bayesの定理からP(Ci = i|x) = P(x = Ci|i)·P(Ci = i)/P(x) fi(x) → P(Ci = i|x) = fi(x)·P(Ci = i)/Σj=1kfj(x)P(Ci = j) → クラスが決まる応用: 手書き文字認識、癌診断 多重応答順列法 (multi-response permutation procedure, MRPP)DFA変法 = DFAの多くの仮定を排除したもの (Williams 1983)正準判別分析 (canonical discriminant analysis, CDA)
= 重判別分析 (multiple discriminant analysis), 正準分析$ (canonical analysis) ステップワイズ判別分析 (stepwise discriminant analysis)1) 前進法(= ステップワイズ判別分析)ステップ毎に判別モデル構築 → 全変数を調べグループ判別に最も有効な変数探す。その変数はモデルに取り込まれ、次のステップに進む2) 後進法backward全変数 → 判別に最も役に立たない変数削除 → [反復] → "重要な"判別有効変数を残す偶然の誇張: よくある解釈間違いで統計的有意水準を額面通りに受け取ること 変数追加削除判断時に考慮中の各変数の貢献の有意性計算 → モデル内に含まれる変数中で判別を最もよく行うもの選択 → ステップワイズ手順は偶然を利用 → ステップワイズ手順の有意水準は第1種の過誤確率(α) (H0 = グループ間差なし)を誤って棄却する確率ではない ボックスのM検定 Box's M test: 3群以上での等分散性の検定 |
|
重回帰分析を序列化 (ordination) に拡張 Def. 正準変量 canonical variable: 合成して得られる変量 (Ex. x1, x2) → 正準変量解釈難しい
Ex 1. 原料特性値s個、製品特性値t個
Ex. sample W Z 目的Ex. 変量(≥ 3) x1, x2組とx3, x4組の間の関係が知りたいZ: x1, x2を合成して得る正準変量 → Z = l1·x1 + l2·x2 W: x3, x4を合成して得る正準変量 → Z = m1·x3 + m2·x4 l, mは正準変量の係数 2群分割された多変数群間で、複数観測値を得た時、群内主成分分析と群間回帰分析を同時に行う→ ZとWの相関係数(正準相関係数)を最大にするl, m求める → 重回帰分析・判別分析一般形 (拡張形)
正準変量Wが1変量 ≡ 重回帰分析 標準化: Z = sW = 1, mZ = mW = 0 → 分散(sZZ, sWW)、共分散(sZW)求める |
sZZ = 1/n·Σi=1n(l1·x1i + l2·x2i)2 = 1, (Van den Wollenberg 1977) 冗長性分析 redundancy analysis, RDA正準相関分析に関連変量群Aの合成正準変量 → 変量群Bの予測(説明)度を示す = 非対称法(従属関係) PCAはRDAの特別な場合 冗長性指数 redundancy propportion累積冗長性指数 cumulative redundancy propotion Def. 冗長性 redundancy, Rleft, Rright ある事象に対応する別事象が複数存在する確率 = 正準変量により共有される分散の比 → 正準相関を2乗し求めた分散の割合とこの割合とをかける Rleft = [Σ(loadingsleft2)/p]*Rc2 ⇔ Rright = [Σ(loadingsright2)/q]*Rc2
p: 1番目(左)集合中の変数数,
標本サイズ大 → R = 0.30の正準相関は統計的に有意 正準因子分析 (canonical factor analysis)正準変量分析 (canonical variate(s) analysis), CVA |
Tの標本分布を考えT = T(X1, X2, … Xn)をある区間Dに落ちる確率を一定値αに設定 (一般に0.01 or 0.05)
棄却域 D = [t, ∞]
棄却域 D = [-∞, t1]∪[t2, ∞]
D = [t1, t2] 有り得ない
