(2026年1月30日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 序列化
[主成分分析, 正準対応分析 (CCA), クラスター分析 , 植物社会学, 統計学, 環境保全学特論]
序列化 (ordination)群集データ解析技術は複雑 (Kent & Coker 1992) → 自然界では植物群集データ自身が多変量
= 生データ raw data matrix 群分析(cluster analysis)と序列化(座標づけ/順序づけ ordination)群集多変量解析 群集の空間・時間上の位置を求めるため用いる手法の総称 → 手法により大きく2つの流れデータ還元 data reduction
データ収集から解析にかけて多くの場面でコンピュータを使用するが、原理を知らずにコンピュータに依存することは危険であり、基本的原理と各手法の長所と短所は少なくとも理解しておかねば、解析とは名ばかりの数遊びとなりかねない (植生)環境傾度分析(environmental gradient analysis)の基本手法群集がある環境傾度に対して示す空間パターンを分析する方法 → |
L地点で群集サンプルをとり、地点j (=1, 2, ..., L)における種iの優占度をnijとする。L地点全部でS種出現すると、それぞれの地点はS次元座標系中の点として位置づけられるが、このL個の点をP(< S)次元座標系中のちらばりとして近似的に表せれば、L地点のもつ情報はS次元より少ないP次元に要約される。P次元に要約したために情報ロスが生じるが、群集データは一般に分析の対象として不適当な部分を含んでいる。具体的には、この不適当な部分とは観察される個々の種個体群優占度の偶然誤差に由来する群集組成変動であって、この変動は分析しようとする群集構造にとっては邪魔(ノイズ noise)である。ノイズ消去し本質的(即ち分析対象となる)情報のみを描出できれば、情報ロスはむしろ望ましい。要約されたP個の変量は具体的な個々の種を示すものではなく描象的特性値である R分析とQ分析R-analysis and Q-analysisQ分析とR分析の結果(因子負荷量)は一致しないことが多い Q分析の問題(Pielou 1984)
|
固有値 eigenvalue と固有ベクトル eigenvectorA := n次正方行列, P := n次正則行列 ⇒Def. 対角化: P−1AP = 対角行列 Def. 変換: B = P-1AP ⇒ Def. 相似: AとBは互いに相似 Def. 固有値(特性値)・固有ベクトル: x ≠ 0, α ⊂ ℜ
α: Aの固有値 Def. 固有多項式: |xEn - A| Def. 固有方程式: |xEn - A| = 0 Th. 相似な行列は同じ固有方程式(固有値)を持つ Pr. B = P-1AP ⇒ |B - λE| = |P-1AP - λP-1EP| = |P-1(A - λE)P| = |P-1||A - λE||P| = |A - λE| // Def. 直交行列: tP = P−1 ⇒ PTh. A (≠ O) = n次対称行列 ⇒
(1) 重複度まで入れn個の固有値もち, 少なくとも1つは0ではない Th. 以下の(1), (2)は同値 (1) Aは対角化可能 ⇔ (2) Aはn個の線形独立な固有ベクトルを持つ 主軸問題: 対称行列を適当な直交行列によって対角行列に変換すること Th. 固有値が全て実数である行列Aは、適当な直交行列Lによって、その固有値を対角要素に持つ三角行列に変換できる Th. 実対称行列Aの固有値は全て実数であるTh. 実対称行列Aの相異なる固有値λi, λjに属する固有ベクトルpi, pjは互に直交する Q. の固有値と固有ベクトル の固有値と固有ベクトルA.__|xEn - A| =  = x3 - x2 - 5x - 3 = (x + 1)2(x - 3) = x3 - x2 - 5x - 3 = (x + 1)2(x - 3)
Aの固有値: -1, 3 |
アイゲン解析 eigen-analysis固有ベクトル及び固有値を求める過程1901: Pearson Kが原理考案 - コンピュータ発展まで普及しない
┏> x x y z x 1 0.643 0.403 y 0.643 1 0.320 z 0.403 0.320 1
f = a1x + b1y + c1z,
大きさ制限 – f, g, hが無限に発散することを防ぐため sfg = (a1a2sx2 + b1b2sy2 + c1c2sz2) + (a1b2 + b1a2)sxy + (b1c2 +c1b2)syz + (c1a2 + a1c2)szx
(sgh, shfについても同様)
sf2 = a12sx2 + b12sy2 + c12sz2 + 2a1b1sxy + 2b1c1syz + 2c1a1szx ∴__(sx2 – λ)a1 + sxyb1 + szxc1 = 0
sxya1 + (sy2 – λ)b1 + syzc1 = 0
= λ(a12 + b12 + c12) = λ
∴ sf2 = λ → λmax = λ1 = sf2 (以下同様) → 単位固有ベクトル – とり方は幾つかある(PCAの型) |
1環境傾度に沿い群集サンプルをとる時に、その傾度に関しもっとも離れた2地点を座標づけのための主軸(1軸)の両端におき、残りの地点をこの間に配列する。具体的環境傾度不明のときでも類似性のもっとも低い2地点を両端におき序列化可能。2次元以上の座標づけも可能だが、結果は3軸程度までしか解釈できない
手順1. 類似度マトリックス作成
Sample__A___Z___K 3. 他のサンプルの主軸上の得点を以下のように算出する:
AZ = l = 1.0 - 0.2, KA = d1 = 0.4, KZ = d2 = 0.6 |
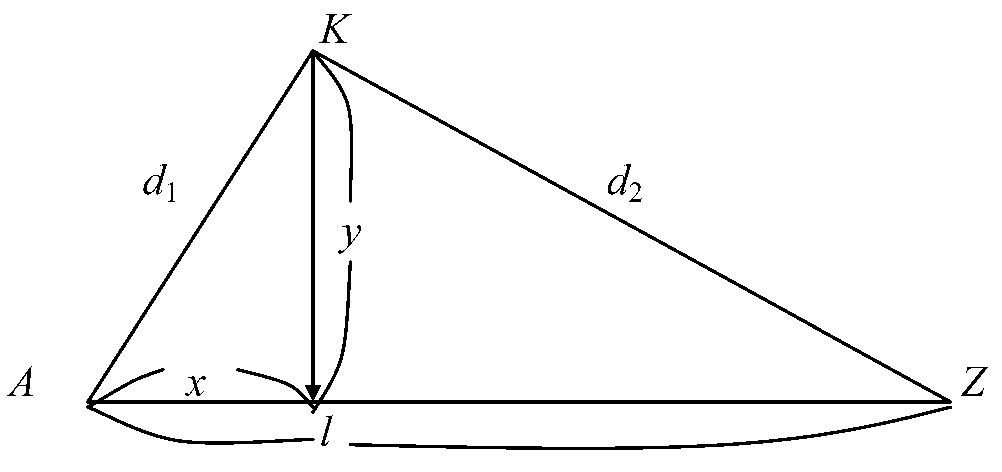 yは地点Kと主軸AZとの距離 → 主軸AZで表される要因以外の効果を反映すると考えられる 寄与率 contribution (rate): 寄与率y大 (lの50%以上) → 更に軸を増やし同様の序列化行うべき |
|
= 反復平均法 (RA) ≈ 数量化III類 ≈ 質的データによるPCA |
反復平均法(reciprocal averaging, RA= 対応分析 (correspondence analysis, CA) (Hill 1973)
統計学で言う「最適尺度法 optimal scaling」のこと |
傾向化除去対応分析 detrended correspondence analysis, DCARA: アーク効果 → DCAにより除去RAの1軸をセグメントsegment分割し、各セグメントが含むyjの平均値を引き第2軸が平均値0を中心とし分布するようセットし直す。これによって形成された2軸をもとに3軸以降を再計算 |
|
相関ある変数を統合した特性値 ≈ 合成得点 = 重みづき合計点
固有ベクトル: 各主成分係数(重み) - 主成分軸解釈する手掛り - 元々の変量
固有値: データ全体のうち、その軸が全体を説明する値
寄与率 contribution (rate): 固有値を%表示 → 累積寄与率cumulative c.r. (cumulative percent) 因子負荷量 factor loading正規化後の固有ベクトル各成分に固有値eigenvalueの平方根をかけたもの 目標: 座標変換(線形変換)からm変数標本データ情報が最も端的に表現される順序にm個の新座標軸を定める= 多変量を少数成分componentに要約
各個体差分離のため分散最大化合成変数(Ex. 多変量線型和)作成
最小自乗法により最適直線を求める方法 → 前提 = 量的データ → L = Σi=1mr2(z, xi) xi: 基準化されたデータ (n データ数)
xi = (xi – mx)/SX,
a for max(L) =
zij = ai1xij + ai2x2j + … + ainxnj |
Def. 主成分得点 principal component score (スコアeigenvector): 第i主成分のj番目(j期目)の値zij
cp = lp/(λ1 + … + λp) → 第p主成分寄与率contribution rate: zによりどの程度xを説明できるかを表す より多くのPCA軸を使うとより小さな比率の変異率(寄与率)しか得られない 修正PCA (modified PCA, MPCA)= 拡張PCAY: n個の個体とp個の変数をもつデータ行列。量的データ(質的データ → 数量化し使用) Y = (Y1, Y2) → (部分行列Y1 = Yをq個変数をもつn × q) + (Y2 = 残りp – q個変数をもつn × (p – q)) (1 < q < p) Y = (Y1, Y2) の分散共分散行列, S =MPCA: Y1によるr個の線形結合 Z = Y1Aが元のp個の変数を最もよく代表するA = (a1, …, ar)を推定(1 < r < q) → 2規準 (Tanaka & Mori 1997)
規準 1: 線形結合zを用いyの予測効率を最大にする MPCA規準利用変数選択: q個変数をもつ変数組み合わせ中、寄与率PかRV係数を最大にするqを見つける 冗長性分析 (redundancy analysis, RDA) |
≈ 因子分析に(非)類似度を導入した拡張版折半法(奇偶法) split-half method(ガットマン折半)信頼性係数(Guttman split-half) reliability coefficient,αxijxk = 2rxijxk/(1 + rxijxk) スピアマン・ブラウン公式 Spearman-Brown formula
r: 相関係数 α = n/(n – 1)·{1 – (Σi=1nsxi2)/sxt2} si2: 各変数の分散, sxt2: 全体の分散 MDS仮定: 1変数(類似度)が複数因子複合体を表現
→ 類似性が対象を表わす点で表現される = 適合度最適となる配置を評価しその最小値を見つけるアルゴリズム Def. (生)ストレス(不適合度) stress (Kruskal's stress), π = Σ[dij – f(δij)]2= 観測距離行列の再現性を評価
dij: 次元を与えた時の再生距離(MDS指定次元数で再現された距離)
= オブジェクト間距離順位再生 ストレス値↓ ⇒ 観測距離行列に再現された距離行列の適合度↑ シェパードダイアグラム: 観測距離に対しある特定次元数を指定し再現された距離をプロットした散布図
X軸 = 元類似性 ↔ Y軸 = 再生された距離 → 負の傾き
再生距離がこの階段関数上に完全に乗る = 距離(類似性)が解(次元)で完全再現 次元数決定因子分析・主成分分析にも適用可一般に、距離行列再現に使用次元↑ ⇒ 適合度↑ (= ストレス↓)
Ex. 変数数 = 次元数 ⇒ 観測された距離行列を完全再現
Ex. 3都市A, B, Cと3都市D, E, Fが次のような距離関係 → 3都市(オブジェクト)の配置 b. カイザー規準 c. スクリーテスト scree test: ストレス-次元数プロット → 使用次元数決定
Cattell 1966: 因子分析因子数決定問題で提唱 → Kruskal & Wish(1978): MDSへ応用 |
配置(布置)の解釈: 解釈次元数決定のための第2基準は最終的布置の明快さ
結果次元が簡単に解釈可能(OK) ↔ プロット点が"曖昧な雲"を形成し直接的次元解釈できない 1) 計量多次元尺度法 metric MDS (MMDS)類似度が比尺度や間隔尺度から得る場合 ≈ PCoA2) 非計量多次元尺度法 non-metric MDS (NMDS)類似度は順序尺度から得る → MMDSよりロブスト
初期布置指定後(Ex. PCA)、生ストレス得た後に逸脱係数(Guttman 1968)最小化に、反復計算を最急降下法 steepest descent method(Schiffman et al. 1981)等で行う
再現された距離と入力データの単調回帰変換の差を最小化が目的
最急降下法で得た値は順位の並べ替えを通じ計算される(Guttman 1986)。各繰り返し後、標準化ストレス(S) (sストレスs-stress (Young's s stress))最小化のために単調回帰変換(Kruskal 1964)で繰り返し計算を実行する 3) 非対称多次元尺度構成法非対称 = 対称行列ではないものEx、A君-B君: A → B (親友と思う) ⇔ B → A (友達と思う) → 2人の(心理学的)距離)非対称 仮定: 非対称類似度行列で、類似度が各対称相互の距離を反映 → 各対象を特定空間中の点で位置づけ 主座標分析, PCO or PCoA (principal coordinates analysis)適訳なし (Gower 1966)= 古典的多次元尺度構成法 classical multidimensional scaling (CMDS) PCA = 正規分布仮定 → 0項多く含むデータに不適 – 比較的均質homogenousなdataではないから
アーチ残る(Gauch 1982) 定式化: (N, M)行列の2対象間の距離行列 E = e(i, j)の各要素に対し aij = eij – mei – meij - met … (1) と変換。mei, meij, metは個々のEのi行、j行、全体平均(2重中心化 double centering)。(1)より aii + ajj – 2aij = eii + eij – 2eij … (2) → 座標を与えるのに、距離行列 E = (eij)、A = (aij)のどちらの固有ベクトルからでも対象間距離は等しい
Ex. A: 行和は0 → A·1 = 0·1 = 0 サポートベクターマシン, support vector machine (SVM)2値判別問題を解くための学習機(判別関数) (Vapnik et al. 1990s')高汎用性 → バイオインフォマティクス
Ex. マイクロアレイデータ判別, タンパク質相互作用解析 |
|
仮説 → 検証: 調査環境因子選択 = 全環境要因測定は不可能 収斂 convergence → データ解析(モデル)におけるズレ
10% variance → due to site |
Ex. 有珠山調査計画 (修論, Tsuyuzaki 2019)
┌──────────────────────────┐
測│ =植物成長= =環境要因= │
定│┏━━━━━━━━━━━┓ │
項│┃ 調査区 ┃ 光(強度) │
目│┃ 被度 ┃ 土壌成熟 │
│┃ 個体数(実生・成体) ┃ (灼熱減量・pH・NPK等) │
│┃ 定着様式 ┃ 土壌移動(測量・侵食ピン) │
│┗━━━━━━━━━━━┛ │
└───↓───────────↓──────────┘
成長 対応関係 変化 ┐追跡
実生定着 ←─→ │
根系発達 ┘
|
|
種データ変異パターン検出に考案されアーチ効果を強力に除く。CCAはordination (RAでもDCAでも可)によって得られたサイト・スコアを目的変数、同じサイトの環境データを説明変数とする重回帰式を作り、得た式によりサイト・スコアを修正する。 必要データ: 調査区の(群集データ = 各種の優占度) + (環境変数) |
Ex. 個体数と被度を組み合わせた解析 (Tsuyuzaki & del Moral 1994) |
|
分類: 手法多種多様 → 互いに密接な関係(原理的に同じで、条件により同一手法となるものもある) 説明変数(独立変数) = 内的基準 目的変数(従属変数) = 外的基準(基準変数criterion variable) 潜在変数 latent variable: 直接観測可能でなく、様々なデータ変動パターンを通し間接的に推測される変数
課題: 潜在変数想定法に任意性あるため数学的に未確立な部分多 →
外的基準あり → 予測・判別問題 + 概括評価規準分析 特殊例: 重回帰、分散・共分散分析、多変量回帰分析、(重)判別分析、PCA, 数量化I-III類 クラスター分析 (群分析, 群集分類, 群形成)異質なものが混ざり合う対象(変数)を、それらの間の何らかの意味で定義された類似度(similarity)を手がかりに似たものを集め、幾つかの均質な集落(クラスターcluster or group)に分類する方法の総称全変数グループ分類 → グループ数/所属クラスター群は未定でデータから探索的判断を繰返し定める 分類法式の一般的性質分類関数 classification function (Lance & Williams 1967)
A. 階層クラスター分析 (hiearchical cluster analysis)= 階層的手法(ヒエラルキー手法) hierarchical method1. 集約方式 agglomerative strategy類似したプロット(= 距離の小さなもの)を順につないで同じクラスターにまとめ デンドログラムを作るa. 単純連結法 single-linkage method マトリックス中で最高類似度の組選び、段々と数値低めグループを拡大する 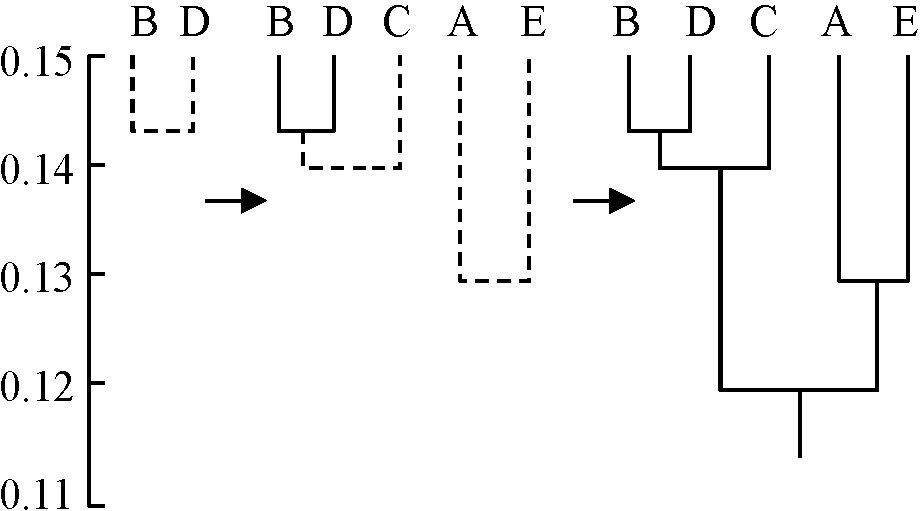
0.144 BD
0.136 BCD (BC)
0.135 BCD (CD)
0.130 BCD, AE (AE)
0.119 ABCDE (CE)
特徴・利点: 簡単 ↔ 不備: グループ構成群中、単一群集の数値に群別が左右される(単調 chaining)可能性 - 不備を補う色々な平均連結法が提案されるb. Mountford平均連結法 Mountford average-linkage method 平均連結法の1種 行列中最も高い類似度群を選び、ついで残りの群集と最初形成された群との間の類似度指数を改めて計算し新行列を作成。次に新しく作成された行列より最も高い数値の群を選び、その群を中心に類似度指数を再計算し、更に新行列を形成する作業を続けデンドログラムdendrogramを完成させる 新しく計算し直されるA, B 2群集間の類似度を計算する式は1/(mn)Σi=1mΣj=1nI(AiBj)で与えられる A群集はA1, A2, …, Ai、B群集はB1, B2, …, Bjよりなり、mおよびnはiおよびjの個数である Ex. Max = B-D: 0.144
BDとA, C, Eの間の類似度指数を再計算
A BD C
BD 0.067
C 0.113 0.136
E 0.130 0.093 0.119
Max = BD-C: 0.136 = (0.074 + 0.113 + 0.059)/3 = 0.082 I(BCD:E) = {I(BE) + I(BC) + I(DE)}/3 = (0.117 + 0.119 + 0.069)/3 = 0.102
A BCD
BCD 0.082
E 0.130 0.102
|
Max = A-E: 0.130 = 0.092 → デンドログラム完成
類似性の最も遠いプロットから繋ぐ方法で、長所は最近隣法と同じ。拡散した樹形図になりやすい欠点 d. 非計量的距離 non-metric distancee. 群平均法 group average method (= 重心法 centroid method)
i) UPGMA (unweighted pair-group method using arithmetic average)
クラスター重心は次元で定義される多次元空間内の平均点 → 各クラスターに対する重力中心 dhk2 = αidhi2 + αjdhj2 + βdij2により群間類似性求まる 欠点: 負の枝negative-branchが出ることがある(Sneath & Sokal 1973) f. 中央値法 median method (= 加重重心法weighted centroid method)クラスターの代表点を元の2つの代表点の中点にとる方法 g. ウォード法 Ward method: 結合で失われる情報量最小群から連結
(実用的に優れた方法? – 工学でよく利用)
変数 ユークリッド平方距離
標本 x y → 1 2 3 4 5 → 1 2 3 45
1 5 3 1 - - - - - 1 - - - -
2 4 4 2 2 - - - - 2 2 - - -
3 2 4 3 10 4 - - - 3 10 4 - -
4 1 1 4 20 18 10 - - 45 18.3 15.3 7.3 -
5 1 2 5 17 13 5 1 -
Str = np/(np + nq)·Spr + nq(np + nq)·Sqr – npnq/(np + nq)2·Spq 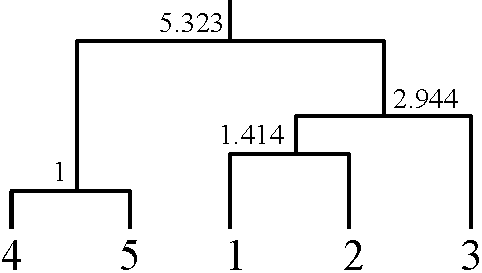
平方距離 距離
1番目[45] 1 1
2番目[12] 2 1.414
3番目[123] 8.667 2.994
4番目[12345] 28.333 5.323
2. 分割方式 divisive method規準に照らして全データを次々と小群に分割していく方法☛ 双方向指標種分析 (TWINSPAN) (Hill 1979) 生物種出現パターンをもとにサンプルと種を同時に二分割していく分類法
指標種 indicator species を見つけ群を特徴づける
あまり見ませんが ... (Carleton et al. 1996) 実測環境データを利用したTWINSPAN拡張版Canonical correspondence analysis (CCA) 利用(TWINSPAN = CA利用) 結果 = [種 × サンプル]表 → 類似分布パターンの種・サンプルが群とし階層的表示 座標付けした時の固有値小さければ分割価値なしと判断 (経験的には上位グループ区分はなじむが元々群集が2又分枝しないとダメ) B. 非階層クラスター分析 (non-hiearchical cluster analysis)= 非階層的手法 nonhierarchical method= 網状分類 reticulate classification 予め分けるクラスター数を初期値として決定 = 対象サンプリング 対象と初期値(代表値)との距離測り対象を適当なクラスターに配置 一度配置し終えた幾つか(か全て)の対象を他クラスターに移す等により「よりよい分割」(クラスター内ばらつきはより小、クラスター間ばらつきはより大)を目指す = 再配分 reallocation → 最もよい組合わせ作る |
[ 植物社会学命名規約 | 特定植物群落調査表 ( 北海道 )]
|
仮定: 群落association間に不連続部分存在 (Brawn-Blanquet 1964) ⇔ 群集は常に連続的変化 → 調査区は隔線設置 → 方法論に問題多
社会単位はどのように形成され、分類すべきか 二つの流派(学派)1. 北欧学派 (⊃ ウプサラ学派)優占種によって群落を区分群落名: 樹林優占種-林床優占種 Ex. トドマツ-オシダ群落(舘脇 操) 優占種明瞭な北方型森林植生で多用 → 林学分野で利用 2. チューリッヒ・モンペリエ学派(ZM学派)= ブラウン・ブランケ法(1964), エーレンベルク法(1963)植物社会学というと、こちらを指すことが多い 種類組成で群落分類 = 森林含む全群落対象 - 広く利用(緑の国勢調査) Br-Bl方法論
植生調査1. 定量的測定a. 個体数、数度(群度)、密度個体数 number of individuals: 調査区内の各種(群)の個体数
単位面積辺りでは個体群密度 population density (密度 density)となる 個体数をとれば個体密度、種数をとれば種類密度となる 数度 (群度 sociability): 大型多年生草本等で個体数測定困難時
肉眼観察で階級分けし方形区内各種の個体数多少を表示 被度 cover: 調査区内の各植物被覆面積 = 植物体外縁を結ぶ投影面積
≠ 厳密な幾何学的地上被覆(投影)面積 |
1: ≤ 1/10 2: 1/10-1/4 3: 1/4-1/2 4: 1/2-3/4 5: 3/4-1 基底被度 basal coverイネ・スゲ等のように束状で生育する植物は、束状をなす部分の基部断面積で表示することがある基底面積 basal area基底面積/胸高直径断面積 = 基底(0 m)あるいは胸高(1.3 m)における断面積。直径と短径あるいは周長を計り(楕)円近似により求めることが多いCf. 被度に関連した指標: 現存量 standing crop(= 生体重 biomass) c. 周期性: 活力度と同じ様な意味で、調査時点での各種の発達状態を記録 周期性表示法例 (記号にこだわらず各自の工夫で調べるべき)
Ass = 栄養成長 b = 蕾 fl = 開花 fol = 花なく葉のみ
調査区全体(か選択区)にある種が出現した度数(個体数とは無関係) 植物群集 = 多種が一定面積内に連関し生活する構造体 → 各種利用生活空間に上限 → 群集は幾つかの平面で仕切られる層の積重ね → 階層
Ex. II (階層名), いわゆる北大式 1 高木層 B1
高木層: 地上より10 m以上 3 草本層 K
高茎草本層 K1: 地上より0.5-1 m 5. 地中層: 地下部 [通常用いる優占度] 優占度 dominance個体数と被度とを組み合わせ、両者を総合的表示 (s.s.)→ 被度数値を平均の計算にそのまま利用できない不便さ 優占度 (Brawn-Blanquet 1964 / Penfound & Howard 1940)
r = 極めて稀に、最低被度で出現する |
|
(※ 序列化で言う「不適合度」はstress) 適合度 fidelityZM学派植物社会学中心概念特定種がどの程度その群集に結びつくか、即ち環境条件を反映するかを度数的に表現。高適合度種ほど群集分類での重要性高い。優占種のみでの群集分類よりはより客観的なものになる。しかし、群集決定の際、最も利用されるのは適合度3の種であり、適合度の有効性は疑問視される 5(適合度) = Treu(専在)の関係 (exclusives) Table β: 環境-群集関係に絶対的なもの存在 4 = Fest(定住)の関係 (selectives) Table γ: 環境と群集とに強い関係 3 = Hold(偏好/選択)の関係 (preferents) Table η: 幾つかの植物群が幾つかの特定群集中において有利に生活 2 = Vag(不定/中立)の関係 (companions) Table ε: 目立った適合性示さない 1 = Fremd(外来/異質)の関係 (accidental): 偶然あるいは過去に存在した植物群落の遺存種 表. 種の適合度決定基準 (Becking 1957): 種の植生単位に対する特異的選択性を反映 → 地理的分布適合度 I II III IV V 問題とする植物群落単位中の値 (%) 0-5 5-50 50-75 75-90 90-100 フロラ的にもっとも近縁な群落単位中の値 (%) 95-100 50-95 25-70 10-25 0-10 I = accidental. II = companies. 1) 標徴種 character species適合度3-5の種が使われるV 独占種 exclusive species, absolute character species: 殆ど完全にある群落単位に限定される種 - 遺存的・孤立的 Ex. 蛇紋岩地植生。石灰岩土壌植生 IV 選択種 selective species, regional character species: 特別な群落単位に偏向を示すが、他群落単位にも出現する種で、しかもこの場合には疎か時には稀に出現する。一般的。気候的に制限された地域
Ex. 日本における選択種
Ex. 山岳・谷・平野・湿地当の各部的な部分で特徴的 + 立地条件 standing condition
→ 乾燥-湿潤、高温-低温等 2) 随伴種 accompanying species, companionsII 不定種: ある定まった群落単位に偏向示さない = 表徴種とならない(Cosmopolitanの多く)3) 偶然種 accidental speciesI 偶然種(偶生種): その群落単位に偶然か遺存的に存在
より好適な生息地をその群落以外に持つ
= 随伴種 (+ 偶然種) ⇒ 適合度低 ≠ 標徴種 |
表. 群集の上位および下位単位の区分
群集: 共通の標徴種をもち一様な相観を持つ群落単位
単位
群団: いくつかの群集を共通の特徴によりまとめたもの 群系 formation: 主に相観により分類した植生単位 = 相観分類 Ex. 常緑針葉樹林・落葉広葉樹林・高茎イネ科草原・マングローブ高木林等の単位が群系に相当する 植生図: 植物群落の分布状態を表わす地図
Ex. 現存植生図、原(元)植生復元図、潜在自然植生図 適合度を生じる要因
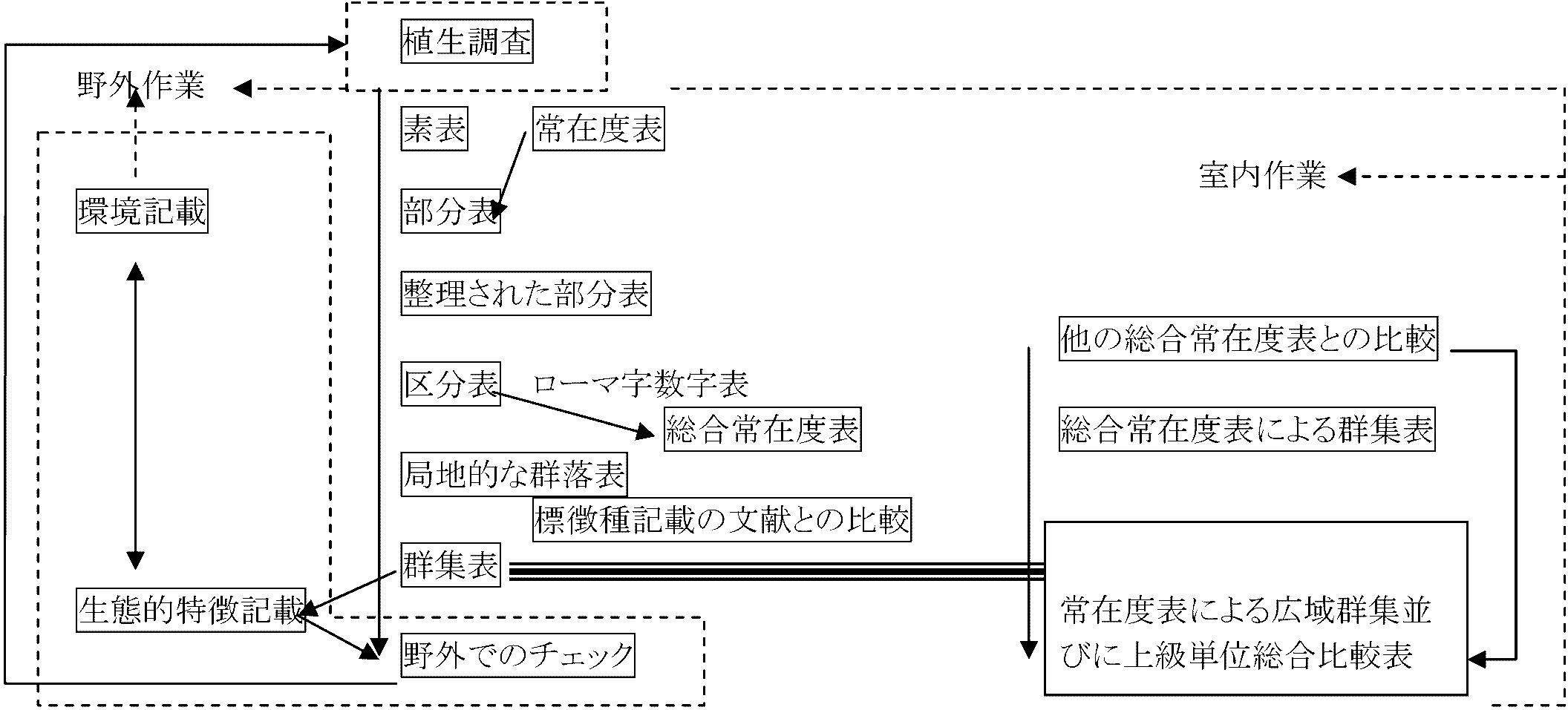 植生調査から植生単位(群集)決定までの系統的なフローチャート → 30%少数配列順位システム(佐々木ら 1973): 群落特性により変える。植物社会学の練習にはよいが、こだわると小手先だけの操作に終わり本質を見失う。広く植生を観て全体を理解し区分に取り組むべき。自分で調べた植物群落調査資料は自分で構成表を作り、自分で考察することが大切で、人に任すと誤りを犯しがち 区分表作成手順群落調査から群落単位を求めるには、植物群落構成表操作により区分表を作り、区分されたもので各単位(大群・小群)等のグルーピングを行う
|