(2021年10月18日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 多様性
種の豊富さ species richnessある群集あるいは調査区内の種数(≈ 種密度 species density = 単位面積あたりの種数)種数の相対的豊富さ
熱帯 → 種数多 → 多様性高 多様性 diversity (Shmida & Wilson 1985)ある群集がどれほど多くの種から構成されているか種数 richness 均等性 evenness or equitability 空間分布 spatial distribution この3要因のうち1つ以上を含むパラメータ 群集多様性のレベル
|
多様性 diversity自然保護へ応用: 群集安定性-相互関係の安定性 → 気候的極相 (climatic climax community)安定群落 = 資源量も安定 → 資源保全上好ましい群集
捕食安定 - 種多様性維持 実際の群集は不安定かつ中期(intermediate stage)が一般的: 雑木林・二次林・草地・湿地・河畔林等 → 中規模撹乱理論 (intermediate theory): 遷移途中相が最も多様性高い(保護必要)。極相を疎かでよいという意味ではない → 島の生物地理学 (island biogeography): 保護区域の考え方 仕組み
|
= 生息地内多様性 (within-habitat diversity or habitat diversity): 生息地 (habitat) における多様性
多様度指数推定法得られたデータの性質を考慮1. 群集小さく、全サンプル識別が可能で個体数カウント可能 1集団における多様性指数なのでαおよびγ多様性の指標となる → 各多様性式がそのまま適用できる 2. 群集大/ランダムサンプル (Basharin 1959): 期待値を求める必要E(H^') = H' – (Q – 1)/2N = –Σi=1npilnpi – (Q – 1)/2N
Q: 全群集の総種数推定値 → E(J^') = E(H^')/lnQ = (H' – (Q – 1)/2N)/lnQ 3. ランダムサンプルではない各調査区内サンプルの順次累積により計算されたH'が調査区増加につれ頭打ち時のH'を採用 Type 0種数 number of index = species richnessType 1種数と総個体数のみに基づく多様性指数Gleason, Margalef, Menhinickなど Type 2: 異質性指数 heterogeneity idnex(a) 均等度 (evenness): 群集における各種の個体数のバラツキを考慮
種-優占度曲線 (species-dominance curve) 仮定: サンプル = ランダムサンプリング + サイズ無限 + サンプル漏れない Ex. 1: トランプ: A 2 3 4 5 6 7 8 9 10 J Q K
任意に1枚とり、それがどれであるかを知るまでに必要な情報量 = 可能性の数W p: 任意の1枚を引いた時に正解である確率 Ex. 2 くじ:______1等__2__3__スカ
_確率 (pi):__p1__p2__p3__p4 H = –Σi=1s(ni/N)·ln(ni/N) (Shannon-Weaver 1949, Good 1953, Pielou 1966) I = 1/N·ln(N!/n1!n2! … ns!) (ブリローウイン式 Brillouin's equation)(Brillouin 1951) [Ni = piN, Nは十分大 → N! ≈ (2π)1/2·NN+1/2·e–N, スターリング近似式] |
I = ln(N!) – Σiln(piN)!
= –NΣipilnpi – (S – 1)/2·lnN – 1/2Σilnpi – (S – 1)/2·ln2π H' = limN→∞(I/N) ≈ –Σipilnpi ≡ Shannon's equation [pi = ni/N]H (or Dn) = I/N, J (or Dm) = I/(NlnS) (S = total number of species) (Margaleff 1957, 1958) Hurlbert (Hurlbert 1971)
均等度指数
→ 多様性, Dm = (N – U)/(N - √N) → ユークリッド距離に関連 Renyiの一般化された情報エントロピー式 generalized entropy N[a] = [(p1ω1 + p2ω2 + … + psωs)/(ω1 + ω2 + … + ωs)]1/(1 – a) = 1/(1 – a)·log[Σkpka/ωkpk]
1/N[2] (arithmetic mean) = log(1/ΣΠ2) SHE解析, SHE analysis (Hayek & Buzas 1997)
分布型考慮不要 + サンプル漏れ認める + ランダムサンプリングの仮定不要 → ジャックナイフを行なうため複数サンプルの抽出必要 Pielouの均等度指数(Pielou 1969), J' → ジャックナイフに似るp1 = p2 = … = pS = 1/S →
H'max = -Σ(1/S·ln(1/S)) = lnS → S↑ → H'max↑ 真の多様性 true diversity闇の多様性 dark diversity偽の多様性 pseudo-diversity 分類学的区分指数 taxonomical distinctness index多様性(5属から計5種5個体) < 多様性(5科から計5種5個体) ⇒種間距離(ωij)に荷重 同種 = 0 (当然), 異種同属 = 1, 異属同科 = 2, 異科同目 = 3, … Average taxonomic distinctness for presence/absence data, Δ+= Σi=1SΣj=1Sωij/{S(S - 1)/2},__i ≥ j, 1 ≤ Δ+ ≤ L - 1 (L, 分類群階級数) Taxonomic distinctness for abundance data, Δ*= Σi=1SΣj=1Sωij·ni·nj/ Σi=1SΣj=1Sni·nj,__i ≥ j, 1 ≤ Δ* ≤ L - 1 系統多様性 phylogenetic diversity, PD系統樹(phylogenetic tree)に基づく多様性
Ex. 葉緑体rbcL遺伝子塩基配列に基づく分子系統樹 |
空間異質性理論と競争・捕食仮説多様性-安定性仮説 diversity-stability hypothesis時間理論と生産力仮説 time theory and productivity hypothesis 1) 時間説 (time theory)多様性の時間的変化(植生遷移系列における多様性の変化)植物群集は遷移が進むと種数増す → 時間と共に多様性増加
Connell & Orias: 環境安定性 → 群集複雑化 100 0 0 0 0 100 0 0 70 30 0 0 0 100 0.4242 0.2653 50 50 0 0 0 100 0.5051 0.3010 80 15 5 0 0 100 0.3384 0.2662 34 33 33 0 0 100 0.6733 0.4771 50 20 15 10 5 100 0.6718 0.4736 20 20 20 20 20 100 0.8081 0.6989
一般に多様性は種数とともに増加。均等に分布するほど大きい 遷移初期における多様性決定要因に関する仮説植物供給源による制限 restriction from plant source植物供給源の量・質に群集の個体数・種数は大きく支配される 遷移初期: 供給起源により多様性が決定されやすい(Tsuyuzaki 1991) ↓ 定着様式による多様性の変化 Scramble competition = Niche先取り説(生存資源に関する競争)Contest competition = Random niche boundary説(この場合は、種-優占度曲線が折れ棒型になる) → ニッチ重複モデル (overlapping niche model): 間接的な競争である 2) 空間異質説 (theory of spatial heterogeneity)空間的に異質なところでは多様性が高い (β-diversity)多様性 diversity 群種を構成する要素のバライエティ → ある群集の競争状態を反映するもの(non-equilibrium theory的立場) 複雑性 complexity diversity ⊂ complexity 空間の相互作用 多様性 + 要素間の関係(競争等) 密度変動型: stability, predictability → constancy 安定性 stability: 定義複数 1. 撹乱に対し系が平衡にとどまる能力 2. 元の平衡への復元能力 3. 安定性は
恒常性 複雑性-安定性ドグマ群集安定性尺度 (Nicholson 1954, MacArthur 1955): 食物網を通って高次の消費者へ流れるエネルギー経路の選択の数 → エネルギーが食物網のあるリンクに停滞することが多い |
___________○
q1 = (1/3)(2/3) = 2/9, q2 = 1/9, q3 = 1/6, q4 = 1/6, q5 = 1/3 → このフロー(or path)がどの位あるのかはcomplexity = stability 経験的事実 (Elton 1958): 群集を人為的に多様化 → 我々にとって望ましい
高次 安定性 多様性
→ 一栄養段階内での種間競争がその栄養段階安定化の機構とし働く 3) 競争説 (競争仮説, competition hypothesis)競争は共存に通じる競争の激しい所ほど多様性高い ↔ 最も競争に強い種が存在すると種間競争小さくないり、その種が優占し種数は減るため、種間競争の激しい状態の方が種数は多い 種間競争を検出するための手順
4) 捕食仮説 (predation hypothesis)捕食者の存在が、捕食者がいなければ最も優占する種を減少させることにより、食べられる側の種間競争を軽減させ種数を増大させる(Paine 1966)5) 生産力仮説 (productivity hypothesis)生産量↑ → 多様性↑ (Tilman 1982)種内競争の効果の方が種間競争の効果よりも強い時に安定共存生じる 生物多様性の緯度勾配 = 一般に、生物の種数は熱帯地域で多く、高緯度地方にいくにほど少ない
アメリカ大陸熱帯雨林木本種数: しばしば300種/0.1 ha ↔ カナダ・アルゼンチン森林: しばしば20種以下 用語adaptability: 適応性innovation: 革新性 rebustness: 頑強性 responsiveness: 応答性・感応性 redundance: 冗長性・余剰性 radpidity: 迅速性 |
熱帯雨林、珊瑚礁における種多様性平衡に近い状態で維持 (Diamond 1978) – diffuse competition → niche 種間競争: もともと効率のよい競争者となれるハビタット – 資源優占 自然撹乱頻度、環境変化速度はperturbationからの回復速度よりも遅い – non-equilibrium あまり効率的でなく適応もうまくできない種の競争排除は、確固たる予測性ある過程ではない。何か他の力が平衡への回復過程を後戻りさせたり、偏らせたり、遅らせたりしている → 平衡理論を群集生態学に適用することの有効性疑問視 仮説: 植物および固着性動物において
群集は平衡状態に達することはなく高い多様性は連続的に変化した結果 非平衡仮説1) 中規模撹乱仮説 intermediate disturbance hypothesis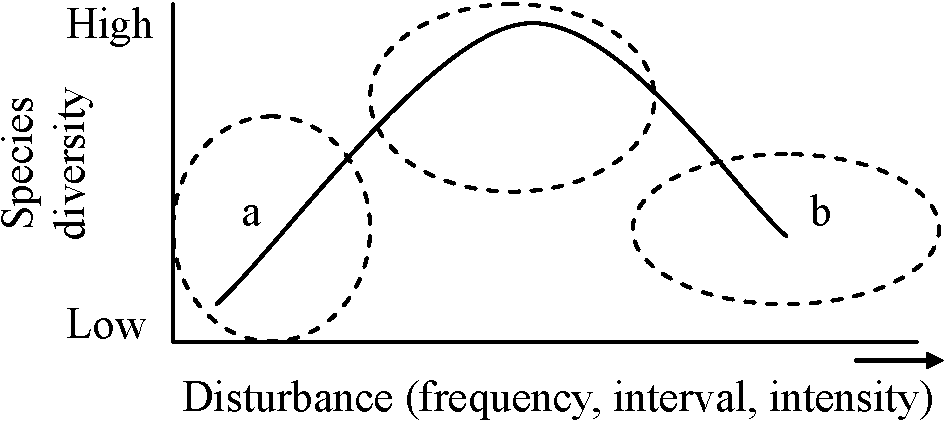
colonizing-mixed-climaxの3ステージに分け多様性調査 1956 Jones: ナイジェリアの森林を調査
→ 高い多様性は森林遷移のnon-equilibrium intermediate stageで見られた |
2) 等機会仮説α-多様性は実在する種数と個体群密度の関数であると仮定するならば、全種は空いた空間へ移住。侵入者に対する抵抗、物理的撹乱、天敵の変化に対する生存能力は等しい 種は様々な能力において異なり、その違いが環境傾度に沿った種の予測性のある分布パターンとなる → 熱帯雨林には合わない (Hutchinson 1957, 他) 3) 段階的変化仮説 gradual change hypothesis種はそれぞれ異なる時期に競争的に優勢になる種間競争で勝つ能力が環境変化により他種の能力以下になる以前に他者を消滅させるだけの時間はない → 多種共存 平衡仮説1) ニッチ多様性仮説 niche diversification hypothesis光・水・栄養における量的変異の傾度土壌型 撹乱によって作り出されるハビタット → 熱帯: 100種以上の種が平衡状態で共存できるのか → 実際に森林では平衡状態に近づくと単一樹種が優占する熱帯雨林ではniche diversificationは共存に対してあまり寄与していない 2) 循環ネットワーク仮説 circular network hypothesisA < B < C < A → 循環遷移 cyclic succession (Watt 1947)3) 死亡率補償仮説 conpensatory mortality hypothesis死亡率が頻度依存であれば競争排除は無限 (predation-avoidance hypothesis)補償による死亡は、ある場合に起こるがmixed tropical rain forestの高多様性維持に重要とは思えない 相対的な重要性は異なるが6つの仮説はいずれも高い多様性を維持するのに貢献している撹乱 + gradual climatic change → local assemblageの変化 → 劣勢競争者消滅回避 → 多様性 → 平衡仮説、非平衡仮説は相互に排他的なものではない
ある程度のα-diversityは平衡状態でも存在する |
|
β多様性 (および系統的多様性) → β多様性の減少 = 均質化 群集比較 interspecific association and similarity between communities = 群集間種間類似度測定(β多様性) → ニッチを反映した多様性、あるいは個体群・群集間多様性 → 群間類似度等により評価 群集類似度(群間類似度) community similarity二元データ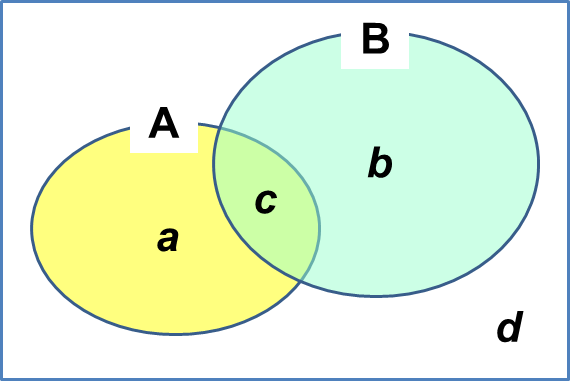 Stand A + / B + → c (= Σi=1nmin(xi, yi): 定量的データ
Stand A + / B + → c (= Σi=1nmin(xi, yi): 定量的データStand A + / B - → a Stand A - / B + → b Stand A - / B - → d 二重ゼロ対偶 (double zero match): dは両方になく、これの解釈で類似度の性質は異なる
Ex. 類似度行列 similarity matrix 群集間類似度選択: 各類似度の一般的性質考慮し選択決定 計量的 (metric)以下の4つの計量空間基準(metric space axiom)を満足する量d(A, B)は計量的である
半計量的 (semimetric)基準1-3を満たすが4を満たさないものEx. 計量的 - ユークリッド距離, 半計量的 - キャンベラ測度 距離 (distance)ユークリッド距離 Euclidean distance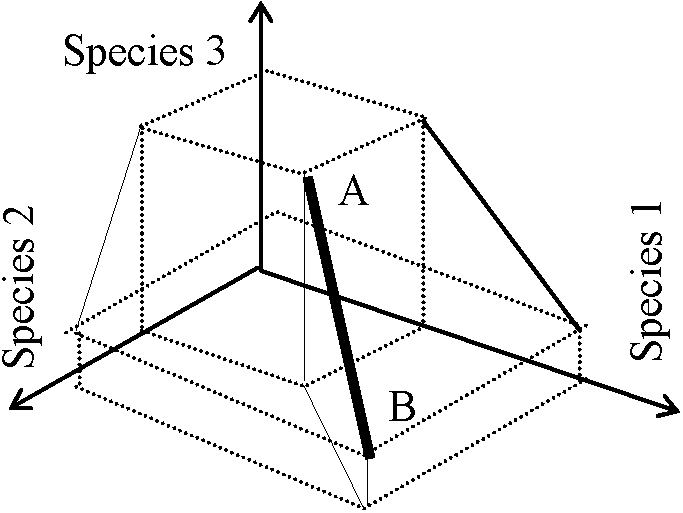 サンプル A, Bにおける種iの優占度をniA, niB (Σi|niA – niB|)1/x ≡ オーダーxのミンコフスキー測度 Minkowski metric = パワー距離 (power metric) x = 1: マンハッタン測度 Manhattan metric (or city-block metric)x = 2: ユークリッド距離 Euclidean distance 3種からなるサンプルAとBの間のユークリッド距離AB → 重みつきユークリッド距離: (Σiwi|niA – niB|)1/2, wi: 重みEx. wi = 1/sii, sii: 変量iの分散 単純マッチング類似度 simple-matching similarity measure
ダイスの類似度 Dice similarity measure i番目のデータの推定値に及ぼす影響 – 感度分析に利用
チュビシェフの距離 Chebyshev distance
ユークリッド距離を分散で正規化したもの 非計量的 (non-metric)森下のCλ指数: 重複度 degree of overlapによる指数 (Morisita 1959)Cλ = 2Σi=1Sn1in2i/{(λ1 + λ2)/N1N2} (0 ≤ Cλ ≤ 1),
λ1 = [Σi=1S{n1i(n1i - 1)}]/{N1/(N1 - 1)} 添字1, 2は地域ではなく種の番号、iが方形区(地域)の番号となる 変数: 個体数の他に各種の重量や被度、Brawn-Blanquetの被度階級等を入れてもよい 利点 = niche overlap式にも用いる (Horn 1966)
|
情報量による指数 (Horn 1966) XおよびY群集におけるShannon-Wiener平均情報量は、それぞれ
H(x) = Σi((xi/X)log(xi/X)), Σixi = X H(X + Y) = Σi(xi + yi)/(X + Y)·log[(xi + yi)/(X + Y)] … (1) ここで(1)式の両群間情報量和の最大値Hmax(X + Y)はHmax = Σi=1(xi/(X + Y)log((X + Y)/xi) + yi/(X + Y)log((X + Y)/yi) である。一方、Hmin(X + Y)は、X = Yのときであるから(1)式よりHmin(X + Y) = Σixi/(X + X)·log{(X + X)/xi} + Σiyi/(Y + Y)·log{(Y + Y)/yi} = Σixi/X·log(X/xi) = H(X) = Σiyi/Y·log(Y/yi) = H(Y) … (2) となるが一般にX ≠ Yであるので最小値はXとYの大きさによって比例配分してHmin(X + Y) = Σixi/(X + Y)·H(X) + Σiyi/(X + Y)·H(Y) … (3) と表現し、また観測地をHobsとすればHobs = H(X + Y) … (4) でHobsは常にHmax(X + Y)とHmin(X + Y)の間をとる →重複度Roは次のように定義できる Ro = (Hmax(X + Y) – Hobs)/(Hmax(X + Y) – Hmin(X + Y)) … (5) 式(5)に(2), (3), (4)を代入しの分母・分子に(X + Y)を乗ずるとRoの分子は
-Σxilog(xi/(X + Y)) - Σyilog(yi/(X + Y)) + Σ(xi + yi)log((xi + yi)/(X + Y)) + log(X + Y){Σixi + Σiyi - Σi(xi + yi)} = Σi(xi + yi)log(xi + yi) – Σixilogxi – Σiyilogyi 分母は-Σixilog(xi/(X + Y)) - Σiyilog(yi/(X + Y)) + XΣi(xi/X)log(xi/X) + YΣi(yi/Y)log(yi/Y)
= Σixilog(X + Y) + Σiyilog(X + Y) - ΣixilogX - ΣiyilogY ((X + Y)log(X + Y) - XlogX - YlogY) 構造的規則性による指数a. Resemblance equation (Prestonのz指数、類似式) (Preston 1962)(a/S)1/z + (b/S)1/z = 1, (0 < z ≤ 1)
S: 2地域(群集)をまとめた総種数、a, b: 2地域個々の種数 導入 [前提] 種数-面積関係: S = kAα → S1, S2の種数面積関係: S1 = kA1α, S2 = kA2αと表せる
if S1+2 = k(A1 + A2)α → 両地域は生態的に均一な地域と考えられる
E = (α1 + α2 – α1+2)/α1+2, 0 < E < 1 Williams modelにおいて総個体数がAおよびBである2サンプルが同一群集から得られたものであれば a = αln(1 + A/α), b = αln(1 + B/α)
が期待される。aおよびbは2つのサンプルにおけるそれぞれの総種数。cを2つのサンプル間の共通種数とすると、種数(a + b - c)における個体数(A + B)のサンプルとの間には
a + b - c = αln{1 + (A + B)/α} の関係を得る。同様に ea/α = 1 + A/α, eb/α = 1 + B/α また ea/α + eb/α = 1 + {1 + (A + B)/α} = 1 + e(a + b - c)/α を得る。ここでI = 1/αと定義すると eaI + ebI = 1 + e(a + b - c)I となる。ここで求めるIがMountfordの類似度指数 非類似度 (dissimilarity) ⇔ 類似度 (similarity)QS (類似度) = 2a/(b + c + 2a) ⇒QSd = 1 - QS (非類似度) = 1 - 2a/(b + c + 2a) = (b + c - 2a)/(b + c) 図示計量群集間類似度 → 類似度行列表示 [多群比較は視覚的に困難]類似度行列: 数値記入法と線影表示する場合を見る ⇒群分析表示 = 全体像把握容易 |
[ 景観生態学 ]
|
生態系または景観単位あたりの多様性 (s.s.) (比較的広範な)対象地域の種多様性 (s.l.) |
α, β, γ多様性間の関係(relationships between α, β and γ diversities)
Community 1: A B C D E F
Community 2: D E F
Community 3: A B E F G
α1 = 6, α2 = 3, α3 = 5 (Veech et al. 2002) αavg + β = γβ = 7 - (6 + 3 + 5)/3 ≈ 2.33 (Baselga 2010) αavg × β = γ ⇐ β = γ/αavgβ = 7/{(6 + 3 + 5)/3} = 1.5 |
|
生態系内で異種の共存・相互作用を知るための概念
Ex. 種多様性、分布、競争、共生 |
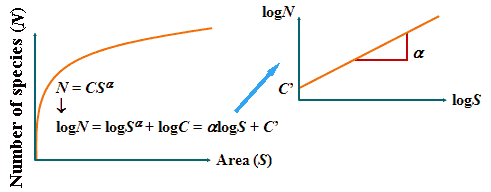 |
種数-(島)面積関係 species-area curveN = CSα → logN = logC + αlogS
N: ある分類群の種数
同面積なら種数は 大陸 > 島 (Darlington 1957, Preston 1960) |
等比級数則 (geometric progression or series)= ニッチ先取説 (law of Motomura's geometric series)1943 内田: Simple competition model
M個の部分からなるある範囲 (area with M compartments)
|ACD
|BD
|ADF
|ACDE
|CE
|BCD |
|A|B|A|A|C|B|
A: n → B: n(1 - n/M) → C: n[1 - n/M - n/M(1 - n/M)] = n(1 - n/M)2 → D: n(1 - n/M)3 …
logMi = logM1 + log(1 - k)i-1 勾配 -a, 切片bの一次式となる(∵ M1 and k = constant) logN = -axn + b (i - 1 = xi) 一次変数なので最小二乗法によりoptimal model決められる → a 群集複雑性 community complexity大 - 順位第1位の種が多く単純な群集 ↔ 小 - 複雑な群集 前提:1) 各構成種の出現確率等しい = 繁殖機会等しい 2) 種間に優劣差ある = 資源(光・栄養塩等)に対する種間競争ある → scramble competition ⇒ 条件満たすには生活型が類似していること 群集全体では成立しくく生活型を層化すると見られる (MacNaughton 1968) 厳しい環境下の少種数群落でよく成立 (Reiner et al. 1971) → resource competition (= scramble competition) この式は発散する - 理論上の難点 |
調和級数則 (law of Corbet's harmonic series)1943 Corbet 1943Sn = C/nm (n = 1, 2, 3 ...)
Sn: n個体よりなる種数
両辺の対数をとると m: 群集複雑性 (a parameter of community complexity)
勾配 -mの一次式: geometric seriesは式的にはharmonic seriesと同等 折れ棒モデル (broken-stick model)= ランダム・ニッチ境界説 (random niche boundary hypothesis)ニッチ空間が直線に例えられると直線上のランダムな点がその直線を分け各線分の長さが各種の占めるニッチに相当する。各線分の長さ、即ち各種の占めるニッチの大きさ(優占度)Ajは Aj = A/S·Σi=1j1/(S - i + 1)
A: 積算優占度 cumulative dominance
前提: 競争(contest competition)の存在 対数級数則 (Fisher's logarithmic series)1943 WilliamsS1(1 + x/2 + x2/3 + …) = S
S = αloge(1 + N/α) α: SとNで決まる常数 → α-diversity index 対数正規則競争 + 多様な要因 → 多種生存に関与する時に成立する傾向(Whittaker & Woodwell 1969)
SR = S0·exp(-(aR)2) (a: constant) |