(2023年10月18日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 数学 > 統計学
歴史と分野Cardano Hieronimo 1501-1576: 「Deludo aleoe」賭けの有利、不利に触れる → 職業賭博師Ggalileo 1564-1642: サイコロ問題 Pascal Blaise 1623-1662: 友人de Mere Chevalierから賭博に関する問 Poisson 1781-1840: 賭けに関する問題が確率論の起こり 仏古典確率論(17c後) statisque
Quetelet Adolphe (ケトレー) 1796-1874, ベルギー: 「人間について」 社会物理学, 「神の秩序」, 天文学 確率論を数学的方法とし広める 独国状学派(19c後) Statistik = 実質社会学説: 統計学の使命(共産圏) = 社会と固有法則を発見(Quetlet批判)英政治算術学(19c後) statistics → 科学方法論(英米流数理統計学19c末): 集団的現象をデータから数理解析 数理統計学 mathematical statistics = 記述統計学 + 推測統計学 (データ解釈) 現実の対象に対し1つの確率モデルを設定し、それに基づきデータ分析をする方法を与える 生物統計学 biostatistics (英農業試験場): 生物学問題を解決する統計学的手法 (Sokal & Rohlf 1995)
生データ(素データ) raw data= 集計や編集などを施していない、最初に記録された状態のままのデータ生ログ: 時系列で得た生データ → 記録対象の現象が確かに起きたことを示す唯一の証拠 (倫理)有用性 = 状況証拠 → 論文に用いなくても追跡参照できるよう保管 Ex. 水位データ(cm): 42.3(フロート深) - 18.6(地上パイプ長)は生データ23.7と記録したら、それは生データではない。42.3 - 18.6と記録 統計分析分析目的に応じたモデル関数に未知係数や誤差項含む特定関数形使用→ 誤差や合成変数が規定される: 誤差2乗和最小化か合成変数分散最大化させ未知係数決定 分析に応じ未知係数に適当な制約条件(Ex. 2乗和 = 1)も課せられる 最小化問題: 平均的変量間関係推定重視 → 殆どの統計分析に問題存在 → 最小2乗法で解決最大化問題: 多変量データmultivariate data全体像を簡潔に特徴付け表現 ↔ 個々の個体の区別を重視 → 多変量統計分析は最小化・最大化という2最適化問題を内包
|
ややこしいのはあちこちに出てるし、ここは基礎の基礎のメモ [ 統計的検定 ] 確率の哲学的基礎に関する問題確率の解釈場 field for interpretation全体(規則性・法則性): 必然 assignable cause → 統計[橋渡し] → 部分(偶然性)
蓋然性 probability (普通"確率"と訳す): 確率的大小stochastically larger or smaller 統計生態学 statistical ecology過度の抽象化を避け、具体的問題への協同的取組みとカウンセリングを重視数理モデル mathematical model数式で表現されるモデル決定論的モデル deterministic model: 初期値によりそれ以降が予測可能 = 方程式によって与えられる Ex. 微分方程式、差分方程式 確率モデル(非決定論的モデル): 初期値が同一でも結果が一つとは限らないEx. 格子モデル 試行 trial, T: 実験・観測・調査等の事象発生操作 事象 event, E: 対象とする現象で発生する事柄(試行の結果のある集合) – 確率が定義されている集合
根元事象 elementary event: 唯1つの標本点からなり分解できない事象 組み合わせと順列 (combination and permutation)Def. 順列: 与えられた複数個のものから幾つかをとり1列に並べたものn個の異なるものの中から任意にr個とった時の順列 nPr = n!/(n – r)! [Case. r = n → nPn = n!/(n – n)! = n] Eq. 漸化式: nPr = n-1Pr + r·n-1Pr-1Def. 重複順列: n個の異なるものから繰り返しを許しr個とり1列に並べたもの, nr (積の法則) Ex. 1, 2, 3, 4の4個の数字を用い3桁の自然数を作る → 43 = 64通り Case. 同じものがある場合の順列
n個のものがc個の組に分けられ、同じ組に属するもの同士は区別できないが、異なる組に属するものは区別できるとき、これらn個を全てとりできる順列の数 → n!/(n1!n2! … nc!) n個の異なるものから任意にr個とった時の組み合わせの数 重複組み合わせ: n個のものから繰り返しを許しr個とる時の組み合わせ
nHr = n+r-1Cr = {n(n+1) … (n+r-1)}/r! (A = 4, WWW, WWR, WRR, RRR) 複数組み合わせ: n個の異なるものをn1個, n2個, …, nc個の組に分ける
n!/(n1!n2! … nc!) |
|
1. 数字の扱い = 標識merkmal: 統計必要事項 = 抽出法。平均mean・偏差 2. 集団(群)group現象観察: 観測対象 - 量的/質的標識 観察の5W (5w for observations): Was 対象(変量・属性), Wer 誰, Wann 時点, Wa 場所, Wie 方法 統計リテラシーよい論文!: 手法誤用 - 信頼性失。誤解釈危険 - 手法選択と正確な記載
問題解は標本種類とサンプル数に依存 [統計分析 = 補助手段 → 問題の本質は考察判断しかない] 記述統計学 descriptive statistics試料の記述・簡略化: 各種現象に表れる集団特徴を標本sample観察結果から数量的に把握記録値 record value: 記録・度数分布frequency distribution → Data x1, x2, …, xn整理(観察結果・資料の整理)
個票データ(個体値) individual data → 標識で階級分類 classification・集計 aggregation → 度数分布表作成 → 集団特徴記述用具設定 → 集団法則・関係提示 度数分布表 frequency distribution tableグラフ化 → ヒストグラム histogram
階級 class: 1, 2, …, k f1/n, f2/n, …, fk/n
累積度数 umulative frequency: f1, f1 + f2, …, f1 + f2 + … + fk f1/n, (f1 + f2)/n, …, (f1 + f2 + … + fk)/n 階級数決定参考式(実際は、外れ値等を考慮し最終決定) ⇒スタージェスの公式Sturges' formula: k = 1 + log2n = 1 + (log10n)/(log102)
k: 階級数, n: 観測値個数 尺度水準と属性 scales and attributes複合データcompound data: リスト、ベクトル
二元データと(定)量的データ (Orloci 1968)定量的データ: 多面的情報包含 → 情報量多
多面的情報包含 → 情報量多
二元データ変換: x > 0 → 1, x = 0 → x = 0 順序統計量→ x1 ≤ x2 ≤ x3 ≤ .... ≤ xn)の特性値1. 代表値 representative= measure of central tendency or average, xrxr: 分布の特徴を表す1つの値 [average 平均の意味 → 統計学 mean] 位置母数 location parameter: 典型値を定める度数分布の位置を示す母数 parameter 代表的位置母数: 3M = 平均 mean, 中央値 median, 最頻値 mode → 中心傾向 central tendency b. モード(最頻値) mode: 多(双)峰型分布形では代表値に不適c. 中央値(メディアン) median: 母集団分布左右非対称時に適切
= x(2n + 1)/2 [n = 奇数] 擬中央値 quasi(-)median → グラフ理論 d. 平均 mean or average |
2. 散布度(バラツキ) dispersion (measure)= 散らばり scatter (バラツキ variability)度合・程度a) 範囲(幅、分布範囲) range, R = MaxXi - MinXi = xn - x1 ⇒ 異常値 Ex. 株価変動幅 b) 分位数 (分位点, 分位値, quantile)Def. ヒンジ(四分位数) hinge or quartile: Q/4分位数
4分位数 quartile__________累積度数 3項平均 trimean (Tukey's trimean): {Q1 + (Q2 × 2) + Q3}/4 → 異常値影響軽減 四分位偏差 quartile deviation (半四分位範囲 semi-interquartile range), Q= 1/2·(Q3 - Q1) 絶対偏差 absolute deviation, ad = Σi=1n(xi - xr): 代表値xrの周りの散らばり⇔ 相対偏差 relative deviation: 変動係数 × 100 (%) c) 平均偏差 mean deviation, d = 1/n·Σi = 1n|D|
偏差 deviation, D = xi – m ∴ Σi=1n(xi – m) = 0, xi: 素(粗)点 = Σi≠j|xi – xj|/(n(n – 1)/2) Def. (ジニ)集中係数 Gini's coefficient of concentration, G = Dm/(2m) = 相対平均差 d) 分散 variance, s2 = 1/nΣi=1nD2標準偏差 standard deviation (偏差 deviation, sd), s = √(1/nΣi=1nD2) Th. Σ(xi – m)2 < Σ{xi – (m + c)}2, c ≠ 0 → 分散(標準偏差)用いる根拠Pr. Σ{xi – (m + c)}2 = Σ{(xi – m) – c}2 = Σ{(xi – m)2 – 2(xi – m)c + c2} = Σ(xi – m)2 – 2cΣ(xi – m) + Σc2 = Σ(xi – m)2 + nc2 > Σ(xi – m)2 // (フィッシャー) z変換 (Fisher's) z transformation標準得点standard score , zi = D/s~N(0, 1) [標準化] 偏差値 deviation score: 偏差値得点(Tスコア T-score), Ti Ti = 50 + D/s × 10 → m = 50、SD = 10に変換 標準誤差 standard error of mean, SEM (root mean square error), se se = s/√n = ΣD2/[n(n – 1)] → × 母集団標準偏差。O 試料平均値標準偏差推定値
一般化分散 generalized variance
___意味____________標本数nの影響__分布仮定 標準誤差率 standard error of percentage (%) = cv × 100
cv = s/|m|, or s/|m| × 100 (%) → データ間ばらつき具合比較 = 2 dataのsが同じでもmの違いにより分散が異なる点を修正 3. 特性値 characteristic value分布型 distribution type を示す量 Ex. モーメント(積率) momentDef. 平均値(原点)の回りのr次モーメント the r-th moment of mean μr ≡ 1/nΣi=1n(xi –m)r (μr = mr → 標本モーメント) r = 1, μ1 = 0r = 2, μ2 = s2 (=分散)
集中度 → 1/nΣi=1n(xi – m)2fi ≤ 1/nΣi=1k(xi – ∀α)2
dy/dα = 1/nΣi=1n2(-xi + α)
歪度(非対象度, 歪み) skewness α3 = μ3/s3 = 1/nΣi=1n((xi – m)/s)3 尖度(尖り) kurtosis α4 = μ4/s4 = 1/nΣi=1n((xi – m)/s)4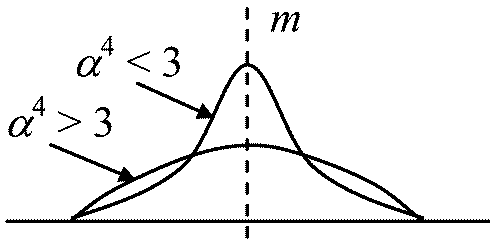 
α4 < 3 尖度強(比較的尖る) |
記録 registration ⇒ データ整理: ノート、写真(スケッチ) + 情報収集
グラフ化ヒストグラム (柱状グラフ, histograms)量の比較を柱状表示(本来、柱互いに密着)ステレオグラム stereogram = 3次元
箱髭図 box-and-whisker plots: 1次元データ要約・比較。最大(小), 第1, 2(中央値), 3四分位, 外れ値等を、「箱」と「髭」で示せる = ヒストグラムの特徴を簡易に示せる 棒グラフ bar graph (chart)量の大きさ、内訳比率の一次元的表示帯グラフ stacked bar chart (compnent bar charts)円グラフ pie chart量の内訳比率を円扇形表示三角グラフ triangular chart3成分比等を表示 Ex. 土性区分 粘土・砂・礫比折線グラフ line chart量の系列変化を表す - 時系列データでは正統的グラフ各種描画法「人」形(集合)で人口、「樽」数で酒産量を表す等、視覚的理解しやすい反面イメージに流れ、不正確で操作される危険も。マスコミ多用(学問的には避ける)ロ−レンツ曲線 Lorenz curve: 分配の不平等度(ジニ係数gini coefficient)を示す下に凸型になるグラフ 散布図行列: 各変数間散布図を更に変数ごとに組み合わせ行列状に配置。多変量データを表すのに便利 高低図 (ハイロウグラフ) high-low charts (graph): 標高等の高低の断面図 レーダー・チャート (正多角形グラフ) radar chart: 360°/n (n: 変数数)と放射状radarに線分出し、それを座標軸表示 |
チャーノフの顔法 Chernoff's face method (顔グラフface graph): 人の顔の表現力利用。顔諸部位に様々なパターンで変数を割当てる。良から悪まで何らかの評価表示時に便利。(応用: 星座や身体を用いる等)
フェイス分析 face analysis: 多変量情報を顔等で表現し視覚化 パレート図 pareto charts (paleto diagram): 統計データを数値の大きい順に並べた棒グラフと、その累積値折線グラフとを合わせた図エスピー表 S-P chart オイラー図 Euler diagram: 一筆書き 解像度 resolution観察幅と誤差に依存 → 詳しく調べれば、従来(左端)と異なる関係が見えてくる 品質管理管理図 control chart: 品質管理に製造工程で部品寸法測定し作成した図nシグマ法 n-σ method: n = 3, 6 …: 管理図作成に利用 μ ± nσの区間推定が意味をもつ場合
計数装置(カウンター) counter: 数を数える装置の総称 |
(単純)算術平均 (相加平均) arithmetic mean, m or x-幾何平均 geometric mean, xg調和平均 harmonic mean, mh= n/Σi=1n(1/xi): 観察値から得た逆数の算術平均の逆数
分子より分母の影響が重要な時使用 複数集団サイズ平均には調和平均が機会的浮動効果検討に適切 算術平均 ≥ 幾何平均 ≥ 調和平均⇒ 一般化平均 generalized mean, m(t) = {(1/n)·Σi=1nxit}1/t limm(t) = xg (m(1) = m. m(-1) = xh) 加重(算術)平均 (重み付き平均) weighted (arithmetic) m, mw= Σi=1nxiwi/Σi=1nwi (w: 加重, ウエイト, 重み)
個々のデータの重要度(重み) weight, wiが異なる → wを反映 累乗平均 power mean, f(p) = 1/nΣi=1nxip もない訳ではない Def. 2乗平均平方根 root mean square, RMS ≡ √(1/nΣi=1nxi2)単位が元の統計値・確率変数と同じになる 指数平均 exponential mean: 指数平滑法によって得られた平均時系列データから将来値を予測 Ex. CD-Rの寿命 調整済平均 adjusted mean: 欠損データ、標本集団測定の時間的なずれ等を調整した平均 |
トリム平均(隣接/刈込/調整平均) trimmed mean: 異常値除去。順位以上
両端p割を除く平均値(p = 1/4 → 中央平均 mid(-)mean) 分散 (variance), s2Def. s2 = 1/nΣi=1n(xi – m)2 = 1/nΣi=1nxi2 – m2Pr. (変数変換transformed fits) s2 = 1/nΣi=1nxi2 – 2(1/n)mΣi=1nxi + 1/nΣi=1nm2 = 1/nΣi=1nxi2 – 2m2 + m2 // r組の試料を合併した時の平均と分散
組: 1, 2, …, r Pr. s2 = 1/nΣi=1rΣj=1n(xij – m)2 = 1/nΣi=1rΣj=1n{(xij – xi) + (mi – m)}2 Th. s2 = sw2 + sB2
sw2: (級)内分散 within variance [試料内分散] |
Def. 統計的現象(確率的現象): 1) 非決定論的, 2) 集団的規則性1) 非決定論的 non-deterministicA → B1, B2, …, Br, …, Bn の何れか - 不確実2) 集団的規則性個体的にはランダム → 集団レベルで規則性標本点 sample point, ωi → 標本空間 sample space, Ω = {ωi} = 全事象 universal event = 全体集合 universe 集合族 set, A: ある集合 → 集合関数: 集合に実数を対応させた関数 → 確率関数 probability function Ex. 確率 P(A) → 確率過程 stochastic process: 設定された確率事象系での時間的変化 Def. 確率 probability
Def. 同時確率 (結合確率 joint probability) ある2つの事象が同時に起こる確率, P(x, y) Ex. 甲乙2人が1個の硬貨を投げ始めに表を出した方が勝ち。甲が先に硬貨を投げ交互に1度ずつ投げる
甲の勝つ確率: 1, 3, …, 2n + 1回目に表が出る
P(A) = P(A1)∪P(A2)∪(A3) … = P(A1) + P(A2) + P(A3) + … Ex. 事象AとBが同時に起こらない → AとBは互いに排反 → A∩B = ∅ P(∪i=1∞Ai) = Σi=1nP(Ai) 有限加法性P(∪i=1∞Ai) = Σi=1∞P(Ai) 完全加法性 → [公理系導入] Def. 完全加法族(σ-集合体, σ-algebra) = A → 1) W ∈ A 2) E ∈ A → EC ∈ A (EC = Ω - E = Ω∪EC) |
3) Ei ∈ A → ∪Ei ∈ A (∪∞)
EC: 余事象 Th. A σ-algebra →1) ∅ ∈ A (∅ = ΩC) 2) Ei ∈ A → ∩Ei ∈ A (∩Ei = ∩i(Ei)C)
∩ 積 product: 積事象 ≡ 共に起こる事象 (交わりintersection) F: 事象, P[•]: 確率測度 Ω ⊂ ∃A, σ-algebraであるiのAに属する任意の事象Eに対し1つのP(E)が対応し次の3条件を満たす
確率の3公理 1. 余事象の法則 P(EC) = 1 – P(E) Pr. Ω = E∪EC, EとECは排反 → P(Ω) = P(E∪EC) = P(E) + P(EC) = 1 ∴ P(EC) = 1 – P(E) // 2. P(∅) = 0Pr. Th.1 → EC := ΩC = ∅ 3. 加法定理: P(E∪F) = P(E) + P(F) – P(E∩F) Def. 完全加法則: P(E∩F) = ∅ Pr. E = (E∩F)∪(E∩FC) … 1, F = (F∩E)∪(F∩EC) … 2
Th. 1におけるE∩FとE∩FC, 2におけるF∩EとF∩ECは互いに排反 Pr. B = (B∩A)∪(B∩AC), P(B) = P(B∩A) + P(B∩AC) ≥ P(B∩A) = P(A) 5. P(E) ≤ 1 Pr. 4)においてB := Ω Ex. 雨が降る確率70% → 雨が降らない確率30% Q. トランプ52枚から1枚選ぶ → スペード(P(A))か絵札(P(B))である確率 A. P(A) = 13/52, P(B) = 12/52 P(A∩B) = 3/52 → P(A∪B) = 13/52 + 12/52 – 3/52 = 11/26 |
|
Def. 条件Bが起こった条件の元でのAの起こる条件付確率
P(B) ≠ 0 → P(A|B) = P(A∩B)/P(B) 相対度数的確率: n回試考 → n回中、事象Bがnb回生起→ このnb回中事象AがnA∩B回生起 多重試行: 連続した試行全体の試行nA∩B/nB = (nA∩B/n)/(nB/n), n → ∞ → 多重試行: P(A∩B)/P(B) = P(A/B) Q. P(A|B) = P(A∩B)/P(B)
[全て条件付確率を一般確率に置き換え証明可能] →
2) 1)と同様P(∅|B) = P(∅∪B)/P(B) = 0 (∅∪B = ∅) ∴ P(Ω|B) = 1 = P(A∩B)/P(B) + P(C∩B)/P(B) = P(A|B) + P(C|B) 独立性 independenceTh. (互いに)独立 independence, ⫫: P(A|B) = P(A) > 0 ⇔ A⫫B独立性の判定 P(A∩B) = P(A)·P(B) → A⫫B
Def. AとBは独立事象independent ↔ 従属事象 Th. 乗法定理(公式): P(A1∩A2∩ … ∩An-1∩An) = P(A1) × P(A1|A2) × P(A3|A1∩A2) × … × P(An|A1∩A2∩ … ∩An-1) Pr. P(A∩B) = P(A|B)P(B), A = An, B = A1∩A2∩ … ∩An-1(左式) = P(An∩A1∩A2∩ … ∩An-1) = P(A1∩A2∩ … ∩An-1) × P(An) = (右式) Def. 因果律: 先に起こった事象が後に起こった事象に影響することTh. 全確率の定理 total probability theorem Ω = A1∪A2∪ … ∪An, Ai∩Aj = ∅ (i ≠ j, 排反), ∃B → P(B) = P(A1)·P(B|A) + … + P(An)·P(B|An) Pr._B = (A1∩B)∪(A2∩B)∪ … ∪(An∩B)P(B) = P(A1∩B) + P(A2∩B) + … + P(An∩B) = P(A1)P(B|A1) + P(A2)P(B|A2) + … + P(An)P(B|An)
P(Ai|B) = P(Ai∩B)/P(B) Th. ベイズの定理 Bayes theorem全確率の定理と同じ条件下 → P(Ai|B) = P(Ai)P(B|Ai)/Σi=1nP(Ai)P(B|Ai)ベイズの規則 Bayes' ruleベイズの定理による確率判断の修正規則 → 定理の持つ意味 = 原因推定A1, A2, … An (事象Sの)原因事象: P(Ai) = 原因Aiの事前確率 prior probability (先見確率) → 事象発生前予測
理論確率 → 事前分布 prior distribution Th'. 事後確率 ∝ 事前確率 × 尤度 likelihood function |
Q. ある製品を作る機械3台 A B C 製品全体rodから任意抽出した製品について、1)不良品である確率、2)それが不良品であることを知った時A製造のものである確率を求めよ A. 1) P(E) = P(A)·P(E|A) + P(B)·P(E|B) + P(C)·P(E|C)
P(A) = 0.2, P(B) = 0.3, P(C) = 0.5 Ex. AA × aa交配で雑種第2代(F2)で表現型[A]を持つ1個体にaaを交配させ5個体F3が出来た。全表現型が[A]であった。交配させられた雑種F2がAAである確率を求めよ A. 1 – 2 × (1/2)5 = 30/32 Ex. "ポリアの壷": b個黒球とr個赤球の入った壷。無作為に1個球を取り出し、取り出された色と同色の球をc個つけ加え壷に入れる。1) かき混ぜ、また1個球を取り出し赤の確率。2) 同様な操作をし3回目に赤の確率 A. 1) B: 黒球が出る事象, B- = R: 赤玉が出る事象 → P(R) = P(B, R) + P(Bc, R) = P(B)P(R|B) + P(R)P(R|R) = {b/(b + r)}{b/(b + r + c)} + {r/(b + r)}{(r + c)/(b + r + c)} = r/(b + r) __2) 同様にP(R) = P(B, B, R) + P(B, R, R) + P(R, B, R) + P(R, R, R)= r/(b + r) 確率行列(統計行列) stochastic matrix= 推移行列 transition matrix: 条件付確率行列のこと状態遷移確率行列(P): 状態i → jの遷移確率 → P(i, j)
Ex. 天気の推移 同時確率行列: 相対度数の行列(クロス表を総度数で割ったもの) ランダムウォーク random walk極微のランダム・ウォーク = ブラウン運動1) (2次元)ブラウン運動 Brownian motion (movement)
顕微鏡下で水面上での花粉粒子の軌跡 = 無秩序 Ex. 水槽中に落とした1滴のインクの拡散 → r = a√t, r: インク滴半径 ブラウン運動過程 Brownian motion process: 確率過程でこの運動表現 逆正弦法則 arcsine law 2) ランダムウォーク: ランダムな±1のみの累積和 = もともと「ギザギザ」
⇚ ⇚ ⇛ ⇛
ブラウン運動もその性質 → 至る所微分不可能 nowhere differentiable a) (繋がり)途切れず b) ギザギザで c) 原因に於てランダムに動く
この3要素満たす現象多 Ex. 株価・為替相場・動物行動軌跡・分子運動 角度統計学 (circular statistics)≈ 方向統計学、円周統計学: 角度データを対象とする統計学Def. 角度データ: 円周上にプロットできるデータ Ex. 風向、樹冠の向き 周期データ(24時間, 季節)に拡張可能 |
|
Def. 確率変数 X (random variable X, rvX): ある試行特性を表わす変量 → Def. (s.s.) X = X(ω), ω ∈ Ω 1) 離散型 discrete rv: Σ___──┼┼┼─┼──┼───> 2) 連続型 continuous rv: ∫_ ───▇▇▇▇▇▇▇────> Def. X = aj, j = 1, 2, … → 確率分布, P(X = aj) 各確率の分布状況を示したもの Def. (確率)分布関数 (probability) distribution functionF(x): 離散型 ∃X → F(X) ⇒ F(x) = P(X ≤ x): Xの分布関数 [discrete: Σxk ≤ kP(X = xk), continuous: ∫-∞xf(x)dx] 1) discrete rvX: x = x1, x2, …, P(X = xk) = Pk, Pk ≥ 0 → ΣkPk = 1(Ex. 2項分布) 2) continuous rvX: 現実には完全なcontinuous rvは不可能Ex. 1枚のコインを投げ表の出る確率を1/2 → 5回投げ表の出る確率をx。分布関数とグラフを書く A. 確率分布, P(xi), X, F(x)
x = 3, 5C3(1/2)5, 2 ≤ x < 3, 16/32
x = 0, 5C0(1/2)5, x < 0, 0 Ex. 生命保険: x歳で加入、n年契約、死亡保険金C円
年利率i ⇒ Def. 現価率 v = 1/(1 + i) B (保険料) = E(Z) = CΣj=1nvjP(j - 1 ≤ X < j) Xの分布が分かればBが求まる → 保険料 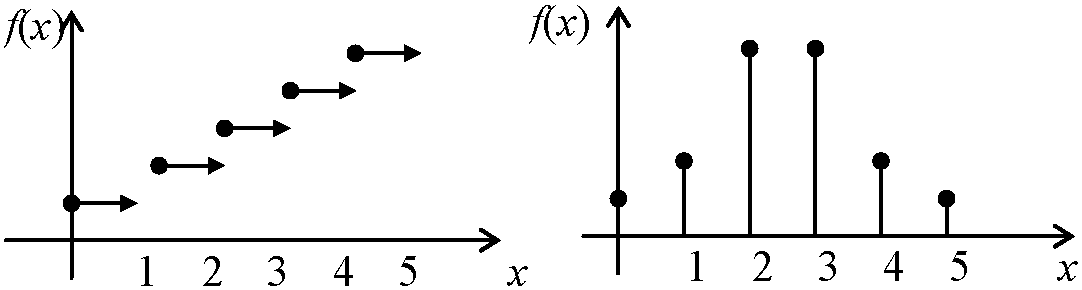 Def. (確率)密度関数 (probability) density function (pdf), f(x): 連続型 グラフ: 決して沈降線をとらない ∃I = [a, b], P(X ∈ I) = P{a ≤ x ≤ b} = ∫abf(x)dx, f(x) ≥ 0 → ∫-∞∞f(x)dx = 1
i) x < 0 → F(x) = ∫-∞xf(x)dx = 0 ii) 0 ≤ x < 1 → F(x) = ∫-∞xf(x)dx = ∫-∞0f(x)dx + ∫0xf(x)dx = 0 + ∫0xf(x)dx = x2 iii) 1 ≤ x → F(x) = ∫-∞xf(x)dx = ∫-∞0f(x)dx + ∫01f(x)dx + ∫1xf(x)dx = 1
分布関数 F(x)・確率密度関数 f(x)の性質1) F(x) = P(X ≤ x), 0 ≤ f(x) ≤ 12) x1 < x2 → F(x1) ≤ F(x2) 単調増加関数 3) P(x1 < x < x2) = F(x1) - F(x2) → F(∞) = limF(x) = 1, limF(x) = 0 rvX分布 := F(x), (F(x)既知) → rvY = G(x)の分布 → 標本分布sample distributionを求める Y = aX + b (a > 0)の分布 ⇒ Yの分布 := G(x)
G(y) = P(Y ≥ y) = P(aX + b ≥ y) = P(X ≥ (y – b)/a) = F((y – b)/a) 確率モデル (具体的確率分布)Def. x1, x2, …, xn → 成功率Pのベルヌーイ試行列 Bernoulli trial≡ 1回毎の事象生起確率pが一定であるとき実験を繰り返し行うこと 以下の3条件満足1) 二元データ binary (0/1データ) ≡ 各回の試行でA, A-の一方のみ生起 2) x1, x2, …, xn: 独立 ≡ 各試行は他の試行に影響を及ぼさない 3) P(Xi = 1) = p: 生起(成功)する
⇔ P(Xi = 0) = q = 1 - p: 生起しない(失敗する)
分布形: J/L/U字形分布 J-/L-/U-shaped distribution 確率分布族1. 離散型確率分布 discrete distributiona. x = 0, 1, 2, …, n2項分布 binomial distributionベルヌーイ試行列におけるn回の試行での確率分布 Bi(∃n, p) (p: 母数) → P(X = k) = nCkpkqn-k k = 0, 1, 2, …, n. p + q = 1, p > 0, nCk: 2項係数 確率分布の確認 Σk=1nnCkpkqn–k = (p + q)n = 1[(p + q)n = Σk=1nnCkpkqn–k: binomial law]
= E[X(k)] = E[X(X – 1)Λ(X – k + 1)] A. 抽出集団中に含まれる罹患者数を確率変数 x f(p) = P(x ≥ 30) ~ Bi(n, p) = Bi(500, 0.05) ベルヌーイ分布 Bernoulli distribution = B(1, p)2項分布で n = 1 多項分布 polynomial (multinomial) distribution, M(n; p1, p2, …, pm) 3通り以上結果 (2項分布拡張一般化) P(X1 = k1, X2 = k2, …, km)
= (n!/k1!k2! … km!)·p1k1p2k2 … pmkm (n = k1 + k2 + … + km), Ex. 3項分布trinomial distribution 超幾何分布 hypergeometric distribution M, N中から非復元抽出でn個取り出す時の確率分布 P(X = k) = nCk·MCn–k/M+NCn n, k, N/(M + N) = p, constant, M + N → ∞ → nCkpkqn-k 2項分布 負の超幾何分布 negative hypergeometric distribution 別名: ベータ2項分布 beta binomial dist., ポリア(-エッゲンバーガ)分布 Polya(-Eggenberger) dist. 階乗分布 factorial distribution スターリングの公式 Stirling's formula ln(n!) = nln(n) – n + 1/2·logn + 1/2·logπ + O(1/n), O(1/n): 定数 スターリング近似: ln(n!) = nln(n) – n b. x = 0, 1, 2, …, ∞ポアソン分布 Poisson distribution, P0(λ) (λ: 母数)P(X = k) = e–k·λk/k! (k = 0, 1, 2, …) ポアソン分布は2項分布の特殊例: 2項分布で期待値 = 分散 → E(X) = Var(X) = λ 上限がない(設定できない)カウントデータ Ex. 種数・個体数ある事象の生起する確率が十分に小さい場合の確率現象に適合 Ex. 株価暴落, ポーカーでロイヤルストレートフラッシュの出る頻度 確率分布の確認 Σk=1∞e-k(λk/k!) = e-kΣk=1∞λk/k! = e–kek = 1(∵ ex = 1 + x + x2/2! + x3/3! + … = xk/k!) 2項分布からポアソン分布導出: np = λ = constant, n → ∞P(X = k) = nCkpkqn–k = {n(n – 1) … (n – k + 1)}/k!·(λ/n)k·(1 – n/λ)n–k = λk/k!·(1 – 1/n)(1 – 2/n) … (1 – (k – 1)/n)·(1 – λ/n)n·(1 – n/λ)–k
-λ/n = x, n → ∞, x → 0, lim(1 + x)1/x = e
低確率で変化する独立試行列の和の分布 ~ ポアソン分布に収束 A. Y = XA + XB ~ P(λ = λA + λB)
P(Y = k) = 1/k!·λk·e-λ, k = 0, 1, 2, … = 1 - e-λ(1 + λ + 1/2·λ2 + 1/6·λ3 + 1/24·λ4) λ := 3 ⇒ 1 - 0.815 = 0.185 [かなり危険] 負の2項分布(パスカル分布) negative bionomial distribution, Bn(λ)2項分布の拡張: 0多、分散大なカウントデータ Def. 複数存在
Case. r = 1 → 幾何分布 幾何分布 geometric distributionベルヌーイ試行列で初めて事象A(success)が生起するに要する試行回数X
NB(1, 1 – 1/p), P(X = k) = pqk-1 (k = 1, 2, ,3 … , p + q = 1, p > 0) → 初項p, 公比qの無限等比級数と考える
別名多 c. x = 1, 2, …, ∞対数(級数)分布 logarithmic (series) distributionf(x; p) = xn/{x·ln(1 – p)}, 0 < p < 1 μ = -p/{(1 – p)·ln(1 – p)}, σ = -(p + ln(1 – p))/{(1 – p)·ln(1 – p)}2 2. 連続型確率分布 continuous distributionpdf f(x)を定めることが目標a. x = (0, 1)一様分布 uniform distribution (短形分布 rectangular distribution), U(a, b)
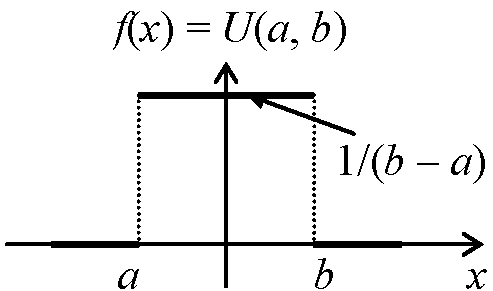
U(a, b) (a, b: 母数) = ∫ab1/(b – a)dx = 1/(b – a)[x]ab = 1 P0(λ)~Bi(n, p) → x~U(-0.5, 0.5) |
Ex. U(0, 5): F(3 ≤ X ≤ 5) = ∫35(1/5)dx = 1/5·[x]35 = 0.4
= β-distribution of first kind, B(a, b) B(a, b) = ∫01ta–1(1 – t)b–1dt
E(x) = a/(a + b) 一般化ベータ分布Bg(x; a, b, c, p, q)
= {|a|xap-1(1 - (1 - c)(x/b)a)q-1}/{bapB(p, q)(1 + c(x/b)a}p+q → B(1/2, 1/2)に等しい Ex. 酔歩モデル、ゲームでの「つき」 b. x = (-∞, ∞)正規分布 normal distribution= ガウス分布Gauss(ian) distribution, 誤差分布error distribution 値の散布度は確率変動のみ → 平均と標準偏差によって記述 N(μ, σ2): μ = ∫–∞∞xf(x)dx, σ2 = ∫–∞∞(x – μ)2f(x)dx
→ f(x) = 1/{√(2π)·σ}·e–(x – μ)2/2σ2 連続的パラメトリック変量(パラメトリック連続変量) continuos, parametric variables 確率分布の確認∫–∞∞f(x)dx = 1/{√(2π)·σ}∫–∞∞e-(x – μ)2/2σ2 [(x – μ)/σ ≡ t, dx = σdt]
= 1/√{(2π)·σ}∫–∞∞e–t2/2σdt [x → ∞ → t → ∞, x → –∞ → t → –∞] → x = μ: Max, x = μ – σ: 偏曲点
σ = constant (μを動かす) → Max変化。恐らく曲線形は変わらない ≡ N(0, 1), f(x) = (1/√2π)·e–x2/2 (s = ± 0), I(x) = ∫0x(1/√2π)e–x2/2dx x = 1.96 → I(x) = 0.95 = 95%, x = 2.58 → I(x) = 0.99 = 99%両側確率: ある分布で、ある値の絶対値より大きい値をとる確率 Ex. N(0, 1), P(|Z| ≥ 1.96) = 0.05 上側(下側)確率: ある分布で、ある値より大きい(小さい)値をとる確率Ex. N(0, 1), P(Z ≥1.96) = 0.025 %点 (パーセンタイル percentile)ある分布関数で上側(下側、両側)確率がQ%となる値 Th. X~N(μ, σ2) → T = (x – μ)/σ~N(0, 1) [~: Xという確率分布は~以下に従う]Pr. Tの分布関数: Φ(t) = P(T < t) = P(X < μ + σt) = 1/√(2π)·σ∫–∞μ+σte–(x–μ)2/2σ2dx = 1/√(2π)∫–∞te–t2dt →set (x – μ)/σ = t ∴ pdf of t is Φ(t) = (1/√2π)e–t2/2 → N(0, 1)のpdf→ 全ての正規分布は標準正規分布に帰着出来る // → 正規分布での標準偏差の意味:
P(μ ± σ) = 0.68__
P(μ ± 2σ) = 0.95__
P(μ ± 3σ) = 0.99 A.__X~N(75, 100), P(X < 60) = P((X - 75)/10) < (60 - 75)/10)) = P(T < -1.5) = P(T > 1.5) = 0.5 - 0.4332 = 0.0668
Ex. 5段階評価法評点 P(μ- 1.5σ < X < μ - 0.5σ) = P(-1.5 < T < -0.5) = 0.4332 - 0.1915 = 0.2417 ロジスティック分布 logistic distributionf(x) = 1/ξ·exp((x – μ)/ξ)/(1 + exp((x – μ)/ξ))2, -∞ < μ < ∞, 0 < ξ < ∞ グンベル分布 Gumbel distribution (二重指数分布) f(x) = 1/ξ·exp(-(x – η)/ξ) – exp(-(x – η)/ξ)), -∞ < ξ < ∞, 0 < ∞ (スチューデントの)t分布 Student's t distribution 平均に関係 t = (m – μ)/√(u/n)~t(n – 1) pdf f(t) = [Γ((n + 1)/2)/{√(nπ)·Γ(n/2)}]·(1 + t2/n)–(n + 1)/2 for ∀t → t(n): t-分布(df = n) E(t) = 0, V(t) = n/(n – 2),
b) n → ∞, t分布はN(0, 1)に近づく u~N(0,1), χ2~χ2(n), u ⊥ χ2 → t = u/√(χ2/n)~t(n),
b) X1, X2, …, Xn~N(μ, σ2), X(= m)~N(μ, σ2/n) = {(m – μ)√(n – 1)}/S~t(n - 1) (Gosset 1908, Fisher 1926) コーシー分布 Cauchy distribution
= t(df = 1), f(x) = (1/π)·(1/(1 + x2)), -∞ < x < +∞ = ラプラス分布 Laplace dist. f(x) = 1/2ξ·exp(1/ξ·|x|), ξ > 0 c. x = (0, ∞)ガンマ分布 gamma distribution (自由度nのχ2分布) f(x, k, θ) = 1/(Γ(k)θk)·xk–1e–x/θ (x ≥ 0), = 0 (x < 0) → pdf ≡ Γ(k, θ)
k: 形状母数 shape parameter (> 0) b) V(X) = kθ2 = k/λ2 Γ分布特殊型: 指数分布､χ2分布､アーラン分布 指数分布 exponential distribution: Γ(λ) or Exp(λ): Γ分布でa = 1
f(x) 指数分布
→ f(x) = λ·e-λx (x ≥ 0), = 0 (x < 0) ∫-∞∞f(x)dx = ∫0∞λ·e–λxdx = λ[e–λx/(–λ)]0∞ = λ{-0/λ – (-1/λ)} = 1 χ2分布 chi-squared distribution: Γ分布でa = n/2 (n = 1, 2, …), b = 2食い違いの測度 ⇒ 分散に関係 Ex. 赤玉白玉が十分に多く、同数入る箱から20個選択 - 赤12個、白8個 期待値: 赤玉・白玉各10個 → 実現値と期待値食い違う = χ2分布 pdf fn(χ2) = 1/{2n/2·Γ(n/2)}(χ2)n/2–1·e–χ2/2 (χ ≥ 0), = 0 (others)→ χ2(n), ∫0∞fn(χ2)dχ2 = 1 a) E(χ2) = n, V(χ2) = 2n, X~χ2(n) → E(X) = n, V(X) = 2nb) χ12~χ2(n1), χ12~χ2(n2) → χ12 + χ12~χ2(n1 + n2), χ12 ⊥ χ22 拡張: ウィシャート分布 Wishart distribution – 多変量解析で使用 アーラン分布 Erlang distribution: Γ分布でaが整数χ2分布統計量 chi-squared statistics a) X~N(0, 1) → X2~χ2(1), X1, X2, …, Xn~N(0,1) → X2 ≡ X1 + X2 + … + Xn~χ2(n) b) X1, X2, …, Xn~N(μ, σ2) → (Xi – μ)/σ~N(0, 1)→ {(Xi – μ)/σ}2~χ2(1) → Σi=1n{(Xi – μ)/σ}2~χ2(n) c) X1, X2, …, Xn~N(μ, σ2) → m = 1/nΣi=1nXi, S2 = 1/nΣi=1n(Xi – m)2→ nS2/σ2 = 1/σ2Σi=1n(Xi – m)~χ2(n – 1) ワイブル分布 Weibull distribution (1939 Weibull)時間に対する劣化現象や寿命を統計的に記述 最弱リンクモデル Ex. 鎖を引く → 最も弱い輪が破壊 = 鎖全体破壊 f(x) = m/η(x/η)m-1·exp{-(x/η)m}
m: ワイブル係数 (形状パラメータ) → m = 1ならば指数分布 → 逆数ワイブル分布(フレシェ分布) / 負のワイブル分布 一般化極値分布 generalized extreme value distribution 代表的3型の極値分布をまとめた確率分布 累積分布関数 F(x; μ, θ, γ) = exp{-[1 + γ·((x – μ)/θ)]-1/γ} 1 + γ·((x – μ)/θ > 0 Ex. 年最大風速の分布
Type 1 グンベル型 Gumbel: γ = 1/n, μ = 0, θ = 1 i) F分布 F distribution (フィッシャー分布) (Fisher 1924) Fs(k1, k2) = B2(k1/2, k2/2; k2/k1) ⇒ 2標本問題 2標本: X1 … Xn1~N(μ1, σ2) (n1), Y1 … Yn2~N(μ2, σ2) (n2)
(mx – my)~N(μ1 – μ2, σ2/n1 + σ2/n2)~N(0, 1) √[1/(n1 + n2 – 2){(n1 – 1)s12/σ2 + (n2 – 1)s22/σ2}] = √{n1n2(n1 + n2 – 2)/(n1 + n2)}·{(mx – my) – (μ1 – μ2)}/ √{(n1 – 1)s12 + (n2 – 1)s22}~t(n1 + n2 – 2) ii) パレート分布: B2(α, β; ξ), x = (1, ∞)正規分布の変形(負値をとらない) i) 対数正規分布 logarithmic normal distribution μ < s2 → 片側にデータが歪んだデータ ii) 逆正規分布 (逆ガウス分布, inverse Gaussian distribution)= ワルド分布 Wald distribution
正(非負)に歪むデータ 混合分布 mixed distribution離散分布と連続分布が組み合わさった分布pdf f1(x), f2(x), …, fk(x) → 離散確率分布 p1, p2, …, pk p(x) = Σi=1kpifi(x) ≡ (有限)混合分布 (pdf)
教師付き学習 supervised learning: 各学習パターン所属クラス既知 |
|
Ex 1. pdff(x) = 1 – |X| (|X| ≤ 1), = 0 (others)
E(x) = ∫-11xf(x)dx = ∫-10x(1 - x)dx + ∫01x(1 + x)dx = 0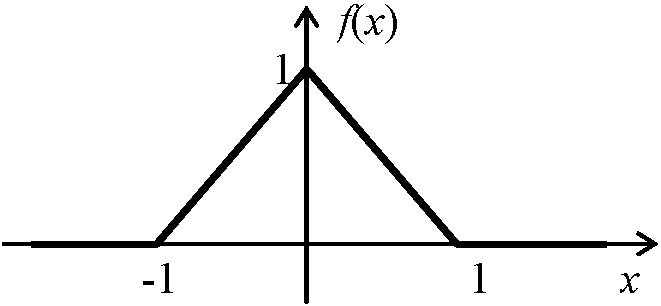 
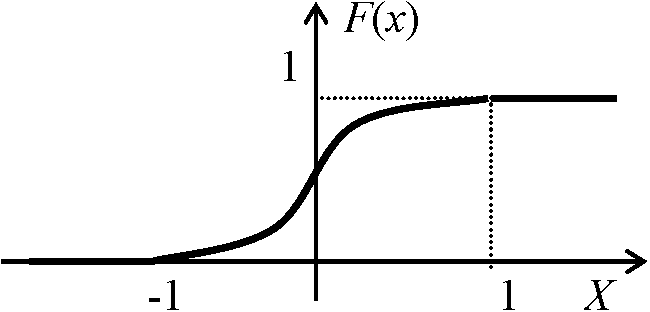 _________密度関数______________________分布関数 Ex 2. X1, X2, … Xn 成功率PのBernoulli試行列 Sn = X1 + X2 + … + Xn (成功回数を表わすrv) → E(Sn), V(Sn)を求める A. Bernoulli試行列は独立性がある
E(Sn) = E(X1 + X2 + … + Xn) = E(X1) + E(X2) + … + E(Xn) = np
∵ E(Xi) = 0·(1 – p) + 1·p = p, E(Xi2) = 02·(1 – p) + 12·p = p V(Xi) = E(Xi2) – E2(Xi) = p – p2 = p(1 – p) = pq Summary: Sn型: 分布名 Sn (定義域), 確率, 平均 E(X) ± 分散 V(X)離散型 discrete2項分布 Bi(n, p)____(0, n) P(X = k) = 0, np ± npqPoisson分布 Po(X) (0, ∞), P(X = k) = 0, λ ± λ 幾何分布_________(0, ∞), P(X = k) = 0, 1/p ± q/p2 連続型 continuous一様分布 T(a, b)__(0, 1),_f(x), (a + b)/2 ± 1/12(b – a)2指数分布 Γ(1, λ)__(0, ∞),_f(x), 1/λ ± 1/λ2 正規分布 N(μ, σ2) (-∞, ∞), f(x), μ ± σ2 Ex. 幾何分布 P(X = k) = pqk-1 (k = 1, 2, …)の平均・分散
Σk=0∞xk = 1 + x + x2 + … + = 1/(1 – x) (|x| < 1), |
Def. 確率母関数 probability generating function: P(X = x) = pi → G(T) ≡ E(TX) = Σi=1npiTi
G'(1) = p1 + 2p2T + … + npnTn–1 = E(X), → 逆モーメント inverse moment Def. キュムラント(累積率) cumulant (= 半不変値semi-invariant), κr
N(μ, σ2) → κr = 0 (r ≥ 3) → μ, σのみで正規分布は表現可 和の分布XΠY, h(x, y), Z = X + Y → f(z) = P(Z < z) = P(X + Y < z)Case. 一様分布: pdfX = f(x), pdfY = g(Y)
→ f(x) = f(y) = 1/(b – a) (a < x < b, or a < y < b), or = 0 (others)
= (z – 2a)/(b – a)2 (2a < x ≤ a + b),
f(x) = 1 – |x| (|x| ≤ 1), = 0 (|x| > 1) → f(t) ≠ g(t) = ∫0τf(t – τ)g(τ)dτ 非心分布 noncentral distribution非心母数 noncentral parameter → 検出力問題と関連
非心ガンマ分布noncentral γ distribution: x = (0, ∞) |
|
Th. 0. チェビシェフの不等式 Chebyshev's inequality: あらゆる分布で成立 平均(m)から標準偏差(s)のλ倍(λ > 0)以上ずれた値の変動 variability (変異 variation)は総度数nの1/λ2以下 Q. 400人に100点満点試験 → m ± s = 45 ± 20 ⇒ 5点以上85点以下人数 A. λ = 2 ⇒ P{|X - m| ≤ 2s} > 1 - 1/22 = 3/4 ∴ 400 x 3/4 = 300 (人)__// Q. 次々に100人に面接: 面接時間/人 = X(分), m = 1, s2 = 0.64 → 既知
1) 各人面接時間は互いに独立な確率変数とし面接終了までの時間Sの平均値と分散を求めよ
E(S) = E(X1 + X2 + … + X100) = 100 = V(X1) + V(X2) + … + V(X100) = ΣV(Xi) = 100 × 0.64 = 64 ∴ s = √V(S) = √64 = 8 __2) k = 3 ⇒ P{(|S - 100|) ≥ 3 × 8 = 24} ≤ 1/32∴ S ≥ 124 or 76 ≥ Sになる確率は1/9以下 Def. {Xn} = X1, X2, … Xn, ∃θ, limn→∞{|Xn – θ|} = 0 (θ = constant > 0) →
{Xn}はθに確率収束 convergence in probability, Xn {Xn}はθに概収束, Xn → θ a.e. (= "殆んど至る所の{Xn}はθに収束") Th. 概収束 converge almost surely → 確率収束 (逆は必ずしも成立しない)弱収束 weak convergence Th. チェビシェフの定理 Chebyshev's theoremTh. (ベルヌーイの)大数の法則 law of large numbers, S Th. コルモゴロフの定理(大数の強法則): {Xn}独立, Σk=1∞V(Xk)/k2 < +∞
→ 1/n·Σk=1nXkはΣk=1nE(Xk)に概収束
→ limn→∞p{(X1 + X2 + … + Xn)/n – p ≥ ε} = 0 → Z = (X + Y)~N(μ1 + μ2, σ12 + σ22) 拡張: X1 + X2 + … + Xn independent, Xi~ N(μi, σi2)→ Σi=1nCiXi~N(Σi=1nCiμi, Σi=1nCiσi2) C: 定数 Pr. 特定関数(和の分布関数)を用いる: X~N(μ1, σ12), Y~N(μ2, σ22) →(X + Y)~N(μ1 + μ2, σ12 + σ22) = (-3X + 4Y)~N(-3μ1 + 4μ2, 9σ12 + 16σ22) Th. Xの分布, X1 + X2 + … + Xn: independence, Xi~N(μ, σ2) 同一分布 →m = 1/n·(X1 + X2 + … + Xn)~N(μ, σ2/n)
Pr. 正規分布の再生性 → μi ≡ μ, σi2 ≡ σ, C ≡ 1/n |
Th. 中心極限定理 (CLT) (1-3式の内1つ利用出来ればよい) X1 + X2 + … + Xn: independence, 全て同一分布に従う(分布は何でもよいか未知), E(Xi) = μ, V(Xi) = σ2 → 1) Xavg = 1/n·Σi=1nXi ≈ N(μ, σ2/n) 2) Xavg(σ/n) = {√n·(Xavg – μ)}/σ ≡ T ≈ N(0, 1) 3) limn→∞p(a < T < b) = 1/√(2π)·∫abe-t2/2dt Pr. (1) ↔ Sn ≈ N(nμ, nσ2), (2) (Sn – nμ)/(√n·σ) ≈ N(0, 1) Ex. mの分布: m = 1/n·(X1 + X2 + … + Xn), ___Snの総和の分布: Sn = X1 + X2 + … + Xn [利用] 漸近正規性 asymptotically normal: 標本抽出を無作為に十分多抽出 → 標本平均値は抽出母体の母集団分布がどうでも、その確率分布はN(0, 1)で近似可能 → 確率近似(法) stochastic approximation Th. ラプラスLaplraceの極限定理 (2項分布の正規近似): Sn ~ Bi(n, p) → (Sn – np)/√(npq) ~ N(0, 1) Pr. CLT → {Sn – E(Sn)}/√V(Sn) = (Sn – np)/√(npq)~N(0, 1), n十分大Def. 不連続補正: 離散型分布を連続分布近似 ↔ 連続修正(連続補正) continuity correction P(np + a√npq) ≈ I(b + 1/2√(npq)) + I(a – 1/2√(npq)) ⇒ 誤差は上式より小Ex. 1. 面接の例でP(S > 120)を求めよ (CLTを使う) A. Xi, Sの分布未知。S = X1 + X2 + … + Xn (n = 100)
E(S) = 100, V(S) = 64 = P((S – 100)/8 > 25) ≈ 0.5 - I(2.5) = 0.5 - 0.4938 Ex. 2. 75個の数値を測定して小数点以下を四捨五入する時の誤差を求めるA. (Hint) Hint: X1 + X2 + … + Xn → 互いに独立
分布U(-0.5, 0.5)に従うと仮定
Xi~U(-0.5, 0.5), S = X1 + X2 + … + X75の分布 A. Hint: nの最小数を求める A1: 正規分布近似で解く → 2項分布
E(X) = n/2, V(X) = n/4 → E(X/n) = 1/2, V(X/n) = 1/4n ≈ 1 - 2·I(0.1 × √n) ≤ 0.01
I(0.1n) ≥ 0.495 = I(2.58), 99%
P{Y – E(Y) ≥ λ√V(Y)} ≤ 1/λ2, 確率密度関数の近似表現エルミート多項式 Hermite polynomial確率密度関数による直交多項式 orthogonal polynomial (グラム-)シャリエ級数 (Gram-)Charlier series |
母集団 population, π全体集合 universe: 現実に把握できるかどうかを別とした理想の対象集団Def. 母集団 population: 一般に抽出されたある標本に対し、その源泉となる対象集団全体 ⇔ 標本集団 = 時間と場所を特定し実際にサンプリング可能な集団 Ex. ≠ 東京と大阪を1母集団とする Def. 母集団転移: 調査途中で母集団が変化 → 標本理論適用できないEx. 質問内容が最初は回答者家族(の誰でも)、途中から回答者のみ Def. 有限infinite母集団: 大きさNの母集団 {e1, e2, … en}⇔ 無限finite母集団(n → ∞): 理想化状態 rvX (or 分布F(X)): 確定集団 - Xの動きを推定→ 手掛かり= 標本(試料) sample = 任意標本random sample (X1, X2, …, Xn): 大きさNのsample, X: 母集団確率変数
Xと同じ分布をするn個のrv(X1, X2, …, Xn) 標本平均 sample mean 標本標準偏差 sample standard deviation 標本分散 sample variance 母数 parameter: 母集団分布を規定する定数 constant Ex.母平均 E(X) = μ, 母分散 V(x) = σ2, 母百分率 p 統計量(標本特性値) statistic (for inference)Def. 標本関数f(x1, x2, …, xn)を実現するrv(X1, X2, …, Xn) = F(X)→ 通常母集団のある母数推定量(標本関数)とし計算 Def. 統計量 statistic: 標本毎に変動する確率変数 → 統計量分布(標本分布)↔ 母数: 既知でも未知でも定数 Ex. 平均値統計量, m = 1/n·Σi=1nxi分散 s2 = 1/n·Σ(x – m)2, (x1, x2, …, xn) → (X1, X2, …, Xn) m = 1/nΣxi → μ = 1/nΣXi, s2 = Σ(xi – m)2→ σ2 = Σ(Xi – μ)2, [Xi equiv; 基本統計量: xiとXiを区別] 標本分布とランダムサンプリング(無作為抽出)全数調査(悉皆調査, センサス) complete survey, census: 調査対象全調査Ex. 国勢調査 = 母集団全体 → "直接"母集団特性記述 → 標本抽出に伴う誤差等考慮不要 統計法(法律): 目的 = 偽り排除、重複調査の無駄省く、秘密保護→ 指定統計 designated statistics 標本調査 sampling (survey): 調査対象集団から1部分を取り出し調査対象集団情報を得る統計調査法統計的推測 inference: 標本集団 → 母集団全体法則性を見出す手続 標本誤差 sampling error: 標本抽出に伴う誤差 - 調査で必ず生じるEx. 世論調査: 母集団 = 成人国民全員 無作為抽出標本集団調査 - 母集団特性推定 標本抽出誤差は、統計学理論で評価可 - 統計的推測精度を知る 標本(サンプル)サイズ sample size: 大 = 精度↑コスト↑有限母集団 → n ≥ N/[(ε/t)2·(N – 1)/{P(1 – P) + 1}] n: 標本数, N: 母集団数, ε: 推定値絶対誤差, t, P: 母比率 Ex. 母比率50%, 推定信頼度95%, ε ≤ 10% ⇒n ≥ N/[(0.1/1.96)2·(N – 1)/{0.5(1 – 0.5) + 1}] 標本抽出法 sampling層 stratum(–ta): 母集団構成員特性に基づく等質集団Ex. 男女別、職業別 → 層化(層別化) stratification |
1. 復元抽出 sampling with replacement: 重複を許し抽出 2. 非復元抽出 sampling without replacement: 重複を許さず抽出 a. 無限母集団から抽出 = 復元・非復元抽出区別必要なし b. 大きさNの有限母集団から非復元抽出 X1, X2, …, Xn: 独立independentではない → 復元抽出不可 標本抽出(調査)法 sampling survey technique母集団から良い標本を抽出する方法無作為抽出(ランダムサンプリング) random sampling
→ 完全無作為化 completely randomizedは可能か ⇔ 実施容易であり、反復調査を行う場合等や予備調査に用いる 割当抽出 quota sampling: 無作為抽出と有意抽出の折衷的なもの Ex. 年齢構成は母集団と同じだが他は有意抽出 - 結局は有意抽出 無作為化 randomization → 無作為標本
抽出段階の主観排除のため実施(客観性) 1. 単純無作為抽出 simple random sampling「でたらめ」か「公平な籤びきlot原理」で抽出対象決定 → 大母集団で困難2. 層別(層化)抽出 (確率比例層化抽出) stratification sampling層化した各層中から無作為抽出 - 層化により精度が下がることはない
a. 比例割当法: 層の大きさに比例proportionalして各層にサンプル割当 Ex. 全体 → X村、Y町 → Z小学校、A小学校 →○君、×さん 3. 集落抽出(多段抽出) cluster sampling実際的手続きを配慮し最終的調査単位をまとめて抽出集落分割 ≈ 母集団縮図 → ランダムに集落選び抽出集落要素を全て標本 Ex. 小学生100人調査 4. 確率比例抽出 probability proportionate sampling各標本集団の標本数に応じサンプル数を決める方法 ⇔ 等確率抽出5. 系統抽出(等間隔抽出) systematic interval母集団Nに、ある順序で1-Nの番号をつけ、n標本をとるのに最初のk単位中から無作為に1個とり、その後k個おきにとる (抽出間隔 sampling interval)乱数 random numberDef. 乱数: 無規則性(無相関性)数列 → i番目に出るaiは、それ以前のaj (j < i)と無関係に定まるDef. 乱数列 radnom sequence: 数字が無作為randomに並んだもの 1. 一様乱数等確率性: limn→∞(ni/n) = 1/10Ex. 0, 1, 2, 3, … 9 (10数)をrandomに並べる a. 乱数表 randomized table (table of random numbers)0-9の整数が等確率で独立に作られた表 b. 乱数サイ dice: 正20面体各面に0-9の整数が2度示してあるサイコロc. 均一乱数発生器 uniform random number generator (PC不在の時代) d. 擬似乱数 pseudo random number: 計算機中に一定規則で発生
→ 統計シミュレーション statistical simulation Ex. x0 = 1, x1 = 15 × x0, x2 = (x1 × 15) mod (106 + 1) i = 1 … 4使用しない 線形合同法(混合型合同法): Xn+1 = (a·Xn + c) mod m (n = 0, 1, 2 …) mに対し適切なa, cを選ぶと周期(最大の)mで乱数的性質を持つ数列が得られる 2. (擬似)正規乱数正規確率性: limn→∞P{X}~N(0, 1) → 一様乱数から生成可能Ex. 2つサイを振った和の分布 |
|
推定・検定に必要な特殊確率分布 標本分布論 → 確率 P{X1 … Xn ≤ x}を計算 Ex. X~N(μ, σ2/n), xi~N(μ, σ2) Def. 自由度 degree of freedom, df: 母数推定に用いられた独立項の数
≡ (全データ点) – (データから推定された母数の数) 反復と擬似反復 replication and pseudoreplication反復 = n (number of samples)擬似反復 ≥ n → 実験単位の過ちにより実際の反復数よりも多い
原因: 正規性 normality確率プロット(法) probability plotting (method)分位数プロット – あらゆる確率分布適合度を視覚的に判断
y軸: 観測値 → 順序統計量(xi ≤ xj, i < j)
理論値(x) = N(0, 1)の%点
→ 正規normal Q-Qプロット/P-Pプロット 確率紙 probability paper (死語かも)グラフ上で(x, y)をプロットし直線性見ることで分布適合性を判断幾何的手続きで、母数評価可能 正規確率紙 normal probability paper: 横軸に変数x、縦軸に正規分布関数yを目盛るグラフ用紙他にワイブル確率紙等がある ★ 古典的解析 査読のために 正規性検定 normality test正規性仮定した検定 → 正規性確認必要H: f(x), N(μ, σ²)~f(x) データ数多 = n (or k)大 → 棄却域狭くなる → nを妥当な線に置く問題 = 標本数問題 Kolomogorov-Smirnov testコロモゴロフ-スミルノフ1標本検定 Kolmogorov-Smirnov one-sample test理論分布からの予測頻度と比較 N(μ, σ²), μ = m, σ² = s² → m, s²を標本集団から求める H: 母集団分布N(μ, s²) → 母数μ, σ²のm, s²を推定値としてよい
C1, C2, …, Ck → Total
H: 標本は特定分布(理論的に仮定された)母集団から抽出
当人いわく、正規性検定として最も優れる シャピロ-ウィルク統計量, W シャピロ-フランシア検定 Shapiro-Francia testギアリの検定 Geary's test: 自己相関に関連 ギアリ統計量Geary, G クラメール・フォンミーゼス検定 Cramer-von Mises test多変量の正規性検定オムニバス検定 (omnibus test, global test or overall test): 3群以上標本数 sample number標本数問題 → 標本数決定基準
α: 検定有意水準 Ex. 1%, 5%
正規分布 α/2%点 (両側 → 2で割る), zβ: 正規分布β%点 Ex. z0.025 = 1.96, z0.20 = 0.84 定量限界 (不検出): 定量下限 limit of detrmination→ 分析で目的の定量(検定)可能最小量(値) = 通常SDのx倍 (浜田 1999) 外れ値(異常値) outlier他因子から極端に離れた(Ex. Max, Min)要素平均値に影響大 → 中央値・最頻値は殆んど(全く)影響なし 1. 異常値検出異常値ない分布 → 平均値 ≈ メディアン, 歪度(N.d. = 0)・尖度(N.d. = 3)
a) 異常値棄却検定(外れ値検定) Ex. スミルノフ-グラブス検定 2. 異常値処置データを安易に棄却しない → 外れ値生じた真の原因を突き止めるのが先決a) 測定ミス → 再測定 b) 現実(生物学)的異常: 異常値存在明記(箱ヒゲ図) → 統計処理から除く c) 現実値範囲内 – 観測値非正規分布の可能性 → ノンパラメトリック |
正規分布から外れた標本検出法外れ値検出 = 異常値棄却検定 rejection test (of outliers)
1. 観測値が本来非正規分布なら無意味 ロスナー検定 Rosner's test: n > 25, two-sided。R static Ri+1 = |x(i) – m(i)|/s(i) スミルノフ・グラブスの(棄却)検定 Smirnov-Grubbs' test (Grubbs' test)
H: ∀xi ∈ πA~N(m, s) ⇔ K: Maxxi or Minxi ∈ πB sは不偏分散(標本分散) Ti < t → accept H = 最大(小)値は外れ値といえない ↔ Ti ≥ t → reject H = 最大(小)値は外れ値 Ex. 133, 134, 134, 134, 135, 135, 139, 140, 140, 140,___141, 142, 142, 144, 144, 147, 147, 149, 150, 164
μ = 140,σ = 8, 正規母集団 → 20 標本抽出: 測定値中164を検定 → reject H = 164 = outlier 複数個: 1回に1外れ値検出 → 最大値を検定→ 外れ値ならそれを除きn - 1個データで同様に検定(反復) トンプソンの棄却検定 Thompson's testギッブスの棄却検定 Gibbs' test 増山の棄却限界 Masuyama's rejection limits (棄却限界 critical value) 拡張(正規分布以外)分布に適合していないものを検出する (Ex. half-normal plot)標準化(基準化) standardization
正規分布仮定できない(正規分布でも) → ノンパラメトリック検定 データ変換(再表現) data transformation変量間で重み異なる Ex. 非正規分布 → 重み付け必要Ex. 群集調査データ: 超優占種 → これに大きくデータ解析結果が依存する場合実施すべき ボックス-コックス変換 Box-Cox transformation (Krebs 1999)
x' = (xλ – 1)/λ (λ ≠ 0), or x' = log(x) (λ = 0)
x' = √(x + a), a = 0.5 良 (Bartlett 1936) λ = -1: 分数変換 reciprocal transformation
x' = 1/(x + a), a = 0 or 1が多い → λ選択: 対数尤度関数, L = –(v/2)·logesT2 + (λ – 1)(v/n)Σ(logex) → Max(L) [v: df = n – 1, sT2 = σ(x')] 得たλをそのまま採用せず、意味の明らかな近傍の値を採用すべき (片)対数変換(semi-)logarithmic transformation
x' = ln(x + a), 通常 a = 0, 1 → 0値がある, x > 0 → 比率データの両極を引き伸ばす 指数変換 exponential transformation
x' = aex
= inverse sine, sin-1 or angular p: 比率 proportion → 値が0-1間で変動時のみ可能 フーリエ変換 Fourier and inverse Fourier transformation
→ backtransform – フーリエ変換の一種? 還元 reduction: 処理treatmentで変数減少 Ex. シャノン-ヴィーナ多様性指数: 種数・均等度を1値で表現 対数変換 logarithmic transformation1) 片対数変換 semi-logarithmic transformationa) 従属変数: y = aebx ⇒ logy = loga + bx → Y = A + bx (線形式 x-logy平面で直線) b = dY/dx = dlogy/dx = (dy/y)/dx → 時系列ならYの変化率となる b) 独立変数Law. Weber-Fechnerの法則: 同量の反応増加を起こすには刺激は同じ比率で増加させねばならない 2) 両対数変換 (≡ アロメトリー allometry): y = axb今後の課題1. 仮説生成型 Ex. データマイニング data mining↔ 仮説検証型: 多くの統計解析 2. 探索的データ解析 exploratory data analysis, EDA↔ 確認的データ解析 データ構造を探索的に探り出す = モデル構築以前の解析初期期に情報把握
|
|
母集団推定 population estimates: X ≡ 母集団分布
F(x, θ): θ, 母集団未知数 → 標本(x1, x2, … xn)から推定 Def. 標本特性量: 母集団特性量: 母集団分布の何らかの特性を示す量
母平均 μ = E(X)___母分散 σ = V(X) 無限母集団 μ σ2/n (n – 1)n·σ2 V(σ2) 有限母集団 μ (N – n)/(N – 1)·σ2/n N/(N – 1)·(n – 1)/n·σ2 V(s2)* *: 複雑で実用性ない Pr._1) E(m) = E{1/n·(X1, X2, … Xn)}2) S2 = 1/nΣXi2 – m2 = 1/nΣXi2 – {1/nΣXi}2 = 1/nΣXi2 – 1/n2{ΣXi}2
= 1/nΣXi2 – 1/n2{Σxi2 – Σ1≤i≤j≤nXiXj}
Cf. (a1 + a2 + … + an) = Σai2 + 2Σ1≤i<j≤nE(ai)E(aj)
= (n – 1)/n·ΣE(Xi2) – 2/n2·[{n(n – 1)}/2]{E(X)}2 → Fn(x): 経験分布関数(標本分布関数) emprical distribution function Pr. "大数の法則"よりtrivialTh. グリベンコ-カンテリの定理: Fn(x)はF(x)に一様に概収束する ≡ limn→∞P(|Fn(x) – F(x)| > ∃ε) = 0 Th. 大数の弱法則: mn → μ確率収束: サンプル数↑ → 真の平均
X1, X2, …~f(μ, σ2), X1 ⫫ X2 ⫫ …, ∀ε > 0
P(|Yn - μ| ≥ ε) ≤ σ2/(nε2) [チェビシェフの不等式] 良い推定の4条件1) 一致性 consistencyDef. 一致推定量 consistent estimator
n十分大, limn→∞P(|θn^(X1, X2, … Xn) – θ| ≥ δ) = 0 ∃θ > 0 → P(|θn^ – θ| > δ) ≤ P(|θn^ – E(θn^|θ)| > (δ > |E(θn^|θ) – θ|)) ≤ V(θn^|θ)/(δ - |E(θn^|θ)| – θ)2 → 0 // 2) 効率(有効性, 最小分散性) efficiency2推定量: E(S) = θ , E(T) = θ → 2推定量S, Tは共に不偏Def. 効率: e(S; T) = V(S)/V(T) < 1 → SはTより効率がよい → Def. 絶対効率: e(θ^) = Vθ/V(θ^|θ) 平均値の有効性 = データ分布重心 → 最小分散 → 母平均推定値として最も誤差小
利点: 統計学の中心根拠: 最尤性・不偏性に関係する推定理論の根幹 3) 十分性Def. 十分統計量: あるパラメータに関する全情報を含む統計量Ex. θ^ = θ^(X1, X2, …, Xn) → Def. 最適推定量: (1-3)を共に満たす推定量(Fisher)→ 最尤法により求められる 4) 不偏性(不偏推定量) unbias= 偏りがないDef. 不偏推定量(不偏統計量) unbiased statistics (unbiased estimator)
未知母数θ ⇒ 統計量T = T(X1, X2, …, Xn)が存在しE(T) = θの時のθに対するT → θ^ ≡ 不偏推定量 Def. V(∀θ*|∀θ) = Vθ ≤ V(θ^|θ), exist → θ^* ≡ 一様最小分散不偏推定量 σ2未知, 2標本(X1, X2, …, Xm) (Y1, Y2, …, Yn) → E{(Σi=1m(Xi – mx) + Σj=1n(Yj – my))/(m + n – 2)} = σ2 Th. N(μ, σ2), E(X) = μ
→ (標本)平均値推定量(X)は母平均μに対する不偏統計量 → 点推定 = n/(n – 1)·1/nΣ(Xi – m)2 = 1/(n – 1)Σ(Xi – m)2 E(s2) = (n – 1)/n·s2はσ2に対する不偏統計量ではないが、E(u2)は、母分散σに対する不偏統計量 Def. 最良不偏推定量(最小分散不偏推定量) best unbiased estimator:
最もバラツキ小
→ 有効推定量 efficient estaimator ≡ θ^(X)
∂l/∂θ ≡ スコア統計量 score statistic 最尤法 maximum likelihood method, ML点推定の具体的方法Def. 尤度関数 likelihood function: L(θ) = f(x1, x2, …, xn; θ) → θ: 最尤推定量 maximum likelihood estimator, m.l.e. pdf f(x) = f(x1; θ), f(x2; θ) … (xn; θ)のMax(L(θ))となるθ(固定値)求める Def. 対数尤度関数 log-likelihood function, l = logL(θ) = Σi=1nlogf(xi; θ) 尤度関数は積 → 和の形(扱い楽) 最大対数尤度 maximum log-likelihood → 尤度方程式(最尤方程式): ∂logL(θ)/∂θ = Σi=1n∂logf(xi; θ)/∂θ = 0 N(μ, σ2), θ(μ/σ2)より解θ求める → 偏微分 Ex. 成功 s = 6, 失敗 f = 4
→ 成功確率Pの尤度: l = (p)s·(1 – p)f = p6·(1 – p)4 十分統計量 sufficient statisticTh. 分解定理(ハルモス-サベッジの判定条件)
統計量 θ^ = θ^(X1, X2, …, Xn)が十分統計量
pdf f(t) = L(μ, σ2) = 1/{(2π)n/2·σ2}·e(–1/2σ2)Σi=1n(xi – μ)2 Pr. θ^ = θ^(X1, X2, …, Xn)は十分統計量, ハルモス-サベッジ判定条件 (X1, X2, …, Xn) 同時確率密度関数 → f(x1, x2, …, xn; θ) = g(θ^, θ)h(x1, x2, …, xn) θ^* = θ^*(x1, x2, …, xn) → g(θ^, θ)最大, f最大 → θ^*: 最尤推定量 // Th. n十分大 → θ^*~N(μ, σ2), or √(n/τ2(θ))·(θn^* – θ)≈ N(0, 1), τ2(θ) = E{[∂logf(X; θ)/∂θ]2} Pr. S(xi; θ) = ∂logf(xi; θ)/∂θ, μ = 0, σ2 = τ2(q)CLT → 1/n·Σ(xi; θ) ≈ N(0, τ2(θ)/n), n十分大 → (θn^* – θ) ≈ ΣS(xi; θ) // Def. 最小十分統計量 minimal sufficient statistic完備性 completeness (v. 完備であるcomplete) |
推定方式パラメトリック推定 parametric estimation: 適当な統計量を選び標本値と標本分布法則からθを推定
信頼度(限界) conficence limit (危険率, 有意水準fiducal limit) 1. 点推定 point estimationθ = θ0 → ある1つの値がどの位の確率で当てはまるか
推定量 estimator (統計量), T = (X1, X2, …, Xn) → V, U. p (母比率) → m/n (比率), ρ (母相関係数) → r, rk, rs M-推定量 M-estimator: 位置中心推定のための標本平均値と中央値に頑健な最大尤度推定量極値は、中央に近い値よりも少ない重み付け – データ: スソの長い対称分布、極値を持つ → M-推定量は平均値や中央値よりも良い推定値 (a-d: 標本適用重み付け法異なる)
2. 区間推定 interval estimation[T1, T2], P(T1 ≤ θ ≤ T2) = 1 – α
≡ 信頼区間(係数) confidence interval (coefficient)
1) 信頼区間を得ようとするパラメータだけを含む = 他パラメータ含まない → 2') 推定するパラメータだけに関係した分布
Q. σ未知, n = 9, m = 1/n·Σxi = 23, s = 9.55 ∴ (m – s/√n, m + s/√n) ≈ (23 – 3.18, 23 + 3.18) Q. 溶液pHを5回測定し7.92, 7.90, 7.94, 7.91, 7.93の結果を得た。真のpHに対する99%信頼限界を求めよA. σ未知, m = 7.92, s = 0.0158 ∴ (7.887, 7.952) 今後の課題乱数試験 (確率化検定) randomization test現象生起に偶然chance cuase的変動伴う → 確率的現象シミュレーション → 乱数使用コンピュータ指向型統計的推測方法: 解析的導出を大量反復計算 → 推定量標準誤差やバイアス(偏り)推定、信頼区間構成や仮説検定を行う 未知母集団分布を経験分布から推定 → 単純 → 柔軟性に富み広範囲の問題に適用可 解析的解を得るのが困難な多くの現実問題に対し数値的解を得られる → 応用: 共分散構造分析等 変動幅評価サンプリングで得たサンプル異なれば、母集団特性に対する推定値も異なる
反復調査実験 → 結果が大きく変動 = 低精度 ↔ 結果があまり動かない = 高精度
個々の1標本を除いた時の推定量変化を評価
標本nの中から1つ除いた推定量 T(i)(X1, X2, … Xn) (i = 1, 2, …, n) Tnの標準誤差 = √(n – 1)/n·Σi=1n(T(i) – T(·))2, T(·) = 1/n·Σi=1nT(i) 2. ブートストラップ(靴紐かけ)法 bootstrap method (Efron 1979)法螺吹男爵が自分を吊るのに靴紐かけを引いた 分かりやすさと簡便さから現在はジャックナイフよりブートストラップの方を多用 標本集団(x1, x2, … xn)からm(< n)個の標本をランダムにk回抽出したk個の偽標本集団 (通常2000回程度実行) → 平均偽標本集団統計量 → 統計量の性質を調べる a. パラメトリックブートストラップ 推定された確率構造に従う乱数で標本生成 → 統計的仮説検定むき b. ノンパラメトリックブートストラップ
繰り返しを許したデータ再抽出resamplingにより標本生成
カジノ(ギャンブル)で有名なモナコの都市名由来 クロス・バリデーション(交差妥当化, 相互検証法) cross-validation, CVa. 折半法(ホールドアウト法) hold-out method = CV (s.s.)
標本をランダム2分割し一方をモデル構成(母数推定) c. ブートストラップ法 |
ベイズ推定 Bayesian estimation or inferenceθを確率変数として扱う経験的ベイズ(手)法 empirical Bayes (or Baysian) procedure (= 古典的ベイズ法) ハイパーパラメータ hyperparameter 推定法: 事前分布の主観性から推定結果信頼性に不安 → 頑強性改善(Gelman et al 1995): 事前分布を超パラメータで表現 + これに分布導入 各ステップで尤度を比較し更新値取捨(複雑なモデルでも事後分布計算可能) Ex. P(x1, x2, …, xn), p(θ) → p(θ|X1) → p(θ|X2) → … 制限付最尤法 restricted maximum likelihood estimation |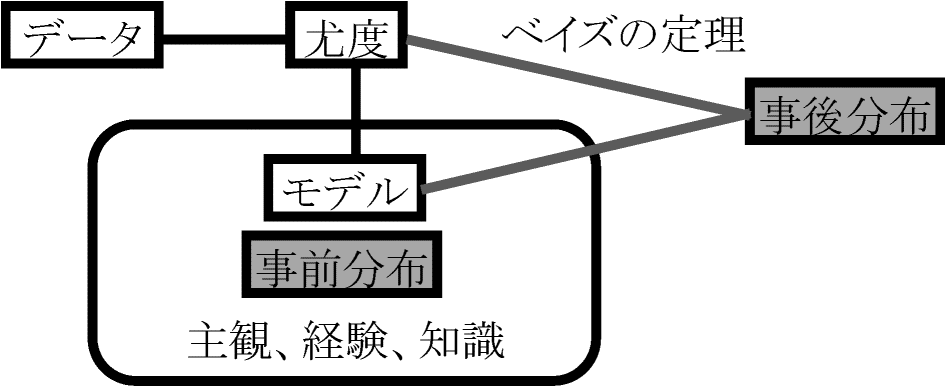
ギッブスサンプリング Gibbs sampling条件付事後分布を利用し、同時事後分布からの確率標本を発生させるマルコフ連鎖モンテカルロ法 (Markov chain Monte Carlo, MCMC)
複雑な多次元分布から乱数を発生させる方法 受信者操作特性 (receiver operating characteristic, ROC)信号処理の概念 → 観測された信号からあるものの存在を判定する際の基準となる特性臨床検査等 → EBM(要曖昧さ回避)の基礎をなすものの一つ ROC曲線AUC (area under the curve) |
|
回帰分析: 独立変数 x ≥ 1 → 1従属変数yを説明
内挿(補間) interpolation ⇔ 外挿 extrapolation
→ 外挿は注意がいる Ex. 時系列分析 一般線形モデル general linear model(SPSSのGLM, 通常GLMは一般化線形モデル)= ANOVA + 重回帰分析 + ANCOVA = 質的独立変数も扱える重回帰分析 Y = a + bX + ε
a, b: パラメータ, Y: 従属変数, X: 独立変数, ε: 誤差(正規分布) |
連結関数 link function |
|
相関 correlation: f(x, y) → y [xが知らされた時にyを推定] x: 説明変数(変量) (独立変数) explanatory variable y: 被説明変数(変量) (目的, 従属, 予測変数) dependent variable → 因果関係: 応答変数 response variable 2度数(次元)の度数分布(相関表)(x, y) = (x1, y1), (x2, y2), …, (xn, yn) (n十分大でのn個の度数分布)最小2乗直線 least square line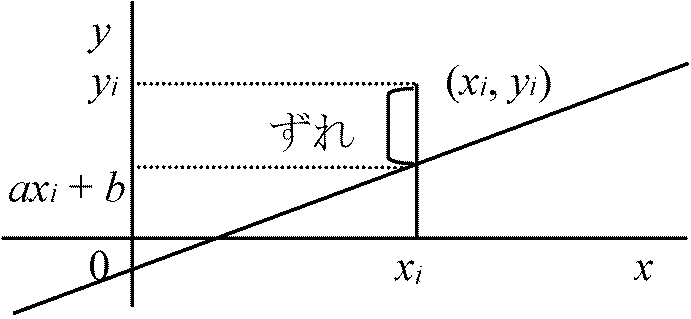 y = ax + b → 1次回帰(線型回帰、直線回帰) linear regression
= 単回帰 simple regression y = ax + bの回りのyの分散, w = 1/n·Σi=1n{yi – (a + bxi)}2 … (1) min(w)なるa, b → ∂w/∂a = 0, ∂w/∂b = 0 → 最小2乗法 method of least squares ∂w/∂b = 1/n·Σi=1n2{yi – (a + bxi)}(–1) = 0∴ 1/n·Σi=1nyi – a(1/n·Σi=1nxi) – b = 0 mx = 1/n·Σi=1nxi, my = 1/n·Σi=1nyi ∴ b = my – amx … (2) (2)を(1)に代入 w = 1/n·Σi=1n{(yi – my) – a(xi – mx)}2 ∂w/∂a = 1/n·Σi=1n2{(yi – my) – a(xi – mx)}{–(xi – mx)} = 0 → 1/n·Σi=1n(xi – mx)(yi – my) – a{1/n·Σi=1n(xi – mx)} = 0 … (3) Def. xの分散, sx2 = 1/n·Σi=1n(xi – mx) Def. yの分散, sy2 = 1/n·Σi=1n(yi – my) Def. xとyの共分散 covariance, sxy = 1/n·Σi=1n(xi – mx)(yi – my) 2変数関係の強さを表す一指標 (3)に代入 a = sxy/sx2 … (4) ⇒ a, b ≡ 回帰係数 regression coefficient(2)と(4)よりy = my + sxy/sx2(x – mx) ⇒ Def. x上のyの回帰直線 ≡ 点(mx, my)を通り傾きsxy/sx2の直線 直線の周りのy軸に平行な分散を最小化= この直線に垂直な方向の分散ではない → 同様、y上のxの回帰直線も求められるが普通は同じ直線にならない一般化最小2乗法 generalized least-squares method, GLS一般化最小2乗推定量 GLS estimator2段階最小2乗法 two-stage least-squares, TSLS 重みなし最小2乗法 unweighted least squares, ULS重み付き(付け)最小2乗法 weighted least-squares method (WLS)
→ WLS回帰 WLS regression 回帰分析 regression analysis説明変数から被説明変数予測Def. 相関係数 correlation coefficient, r ≡ ピアソンの積率相関係数 2変量散らばり度合 = 0次相関 zero-order correlations: 他全説明変数を無視した時の相関 Ex. Pearson, Spearman, Phi (φ) r = 1/nΣi=1n{(xi – mx)/sx}{(yi – my)/sy}= {1/nΣi=1n(xi – mx)(yi – my)}/(sxsy) = sxy/(sxsy) 無名数(単位無) |r| ≤ 1
r = ±1 完全相関
sxy = 1/nΣi=1n(xi – mx)(yi – my) = 1/nΣi=1nxiyi – mxmy Pr. 1/nΣi=1n(xi – mx)(yi – my) = 1/nΣi=1n(xiyi – mxyi – ximy + mxmy)
= 1/nΣi=1nxiyi – 1/nΣi=1nmxyi – 1/nΣi=1nximy + 1/nΣi=1nmxmy rxy = ruv; (xi, yi) → (ui, vi) → mu, mv → ruv (uとvの共分散) 回帰直線(線形回帰) linear regression一方の変量から他変量の平均的値を推定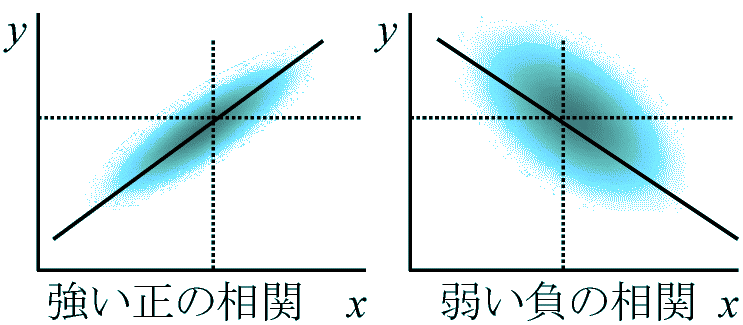
 
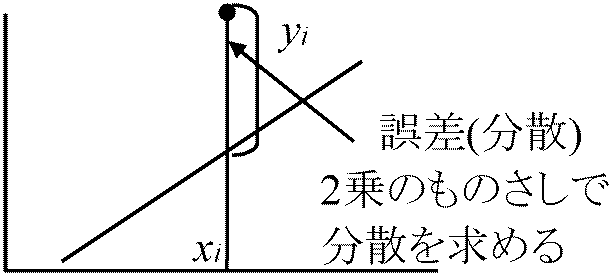分散が異なっても同じ回帰直線が表れる → 推定誤差 error of estimation→ 回帰直線の回りの分散 勾配異質性 heterogeneity in slope 散布図(相関図) correlation diagram, scatter plots (diagram)2変量xとyの関連を示す図sy = 1/nΣi=1n[yi – {y + r(sy/sx)(xi – mx}2] = 1/nΣi=1n[(yi – my) + r(sy/sx)(xi – mx)]2 = sy2(1 – r2) sy2 ≥ 0 → 1 - r2 ≥ 0 ∴ -1 ≤ r ≤ 1,|r| = 1, sy2 = 0: 全変量回帰直線上(完全相関) ⇔ r = 0, Sy2 = sy2 = 0 ∴ y = my: y-x間関係推定不可能 Σi=1n(xi – mx)(yi – my)> 0: 正 positive, < 0: 負 negative, = 0: 無相関 no correlation 線形回帰 y = a1 + b1x, y = a2 + b2xのa, b間の有意差検定a: 勾配の検定 testing slope (平行性の検定 test of homogeneity of slopes)n = 2 (two samples): 回帰係数値(平均値)とその標準誤差を用いF検定 df = n1 + n2 – 4 Fs = (b1 – b2)2/{(Σx12 + Σx22)·sxy}
sxy: 2グループの加重平均(標本数異なれば標準誤差を標準化) その各々について検定比較する必要 n ≥ 3: 回帰係数値の直接検定不可 → 共分散分析(ANCOVA) y軸(従属変数)をx軸(連続変数)と種(名義変数)の2説明変数で要因分析 x軸と種間に相互作用 = x軸に伴うy軸の増加が種ごとに異なる → 傾きbに有意な種間差 相互作用なし: 分散分析構造模型から相互作用項除き、x軸に伴うy軸増加は種間で等しい仮定の元で検定をやり直す → 種間に有意差 = 切片aが種間で異なる 傾きに有意差 → 切片検定できない ホランダーの検定 Hollander test for regression lines 回帰直線の平行性に関する推定と検定 回帰モデル regression model= 一般回帰モデル general regression model
Def.: εi: 誤差項 error term (残差 residual) → (Yi – yi) ≡ 予測誤差 error of prediction 条件: 1) εiΠεj (i ≠j)
_2) εiの期待値(平均)は0 → 推定結果信頼には誤差項に系列相関なしが前提 0) 影響力係数: hi = 1/n + (xi – mx)2/Σx2 comb.
基準化された残差, dyx/s = dyx/(syx·√(1 – hi)) D-W比 Durbin-Watson ratio, DW = Σ(et – et–1)2/Σet2 線形モデル linear modely = f(x) + ε → 理論的簡略さのため未知係数に関しよく使用される変量間平均的関係から個々標本個体の変量間関係は逸脱 → 関係不規則性を誤差項(ε)が集中代表 |
線形式: Y = a + bX [線形回帰] → Y = a + b1X1 + b2X2 [重回帰] トービット分析: 打ち切りのある回帰モデル 分位回帰 quantile regression, Q-regression
従属変数全データではなく、ある一定範囲のデータ(分位)に絞り、それと説明変数との相関を見る。従属変数分布特定する必要なく幅広く利用可 
曲線回帰分析 cursive regression analysis線形回帰に帰着できるDef. リンク関数(連結関数) link function: 式変形し線形にする関数 多項回帰: Y = a + b1X1 + b2X22 X22 := Z → Y = a + b1X1 + b2Z → 線形 指数曲線 exponential curve: Y = ea+bX
対数変換 → lnY = a + bX → 線形
(0 < ρ < 1, β < 0) Mitscherlich則: y = a + b(ρx) = a + b(e-cx) 修正指数 modification indices 非線型回帰分析 nonlinear regression analysis現象に非線形関係(推定) → 線形回帰ではいけないEx. 線形対数モデル(対数線形モデル) log-linear model Ex. 多次元分割表 multi-way (テスト要因 test factor) 非線型回帰モデル nonlinear regression model回帰関数 regression function, yi = f(α, β, γ, xi) + ei (i = 1, 2, … n)
f: regression function, α, β, γ: 母数 平滑化(スムージング) smoothing原データ系列のノイズnoiseをとり平滑化smoothingし宿約化する方法移動平均 moving average (running mean), MAk = 1/j·Σi=k-2/jk+2/jxi (k: 求める移動平均の項 j: 前後の項数) 荷重移動平均 weighted moving average: 近傍に荷重をかけた移動平均 Ex. 指数移動平均 exponential moving average 回帰(方程)式 regression equation回帰分析で観測値(x, y)の分布を近似的に表す方程式母回帰係数 population regression coefficient Ex. y = ax + bのa, b ⇔ 標本回帰係数 1) パラメトリック: スプライン回帰、Box-Cox変換等 a) 多項式回帰 polynomial regression: y = a + b1x + b2x2 + … + bnxn n = 2 → 2次多項式回帰: x2 → √x, logx, 1/x等を使うこともある b) スプライン(区分多項式)関数 spline function
連続条件を満たしつつ接続した区分多項式(補完法) 回避法: 近似区間を小区間に分け、各区間上で相対的に低い次数 lower order 多項式で近似 → 良好な次数 better order (同じ次数 same order) (3次が良く使われる) 2) 非パラメトリックa) プリンシパル曲線 principal curves ⊂ 平滑化曲線
説明変量/目的変量区別不明確 → 外的基準ないデータに対し、一般的な曲線あてはめ手法少ない
射影ステップ: 各データ点から折線上の最近隣点を探索する必要 = 局所的荷重をした平滑化 (LOWESS or LOESS) c) カーネル平滑化: 確率密度関数生成使用曲線の形状を推定 変量関係の分布Def. 同時確率(結合確率) joint probability: ある2事象同時生起確率, P(x, y)Ex. サイコロを2回投げる: 1回目の実現値をa, 2回目の実現値をb 1) 1, 2回目共に1が出る確率 → P(a∩b) = P(a)P(b) = 1/6·1/6 = 1/36 Def. 周辺確率 marginal probability: 他事象に関わりなく1事象だけに起こる確率 (= 条件なし確率)2) 1回目の目が1から6で2回目の目が1 → Σi=16(1/6)·(1/6) = 1/6 Def. 同時分布(同時確率/結合確率/結合分布) joint (probability) distribution:
X = x1, x2, …, xm, Y = y1, y2, …, yn
ΣjP(X = xi, Y = yj) = P(X – xi) = pi → Xの周辺分布 marginal distribution (周辺確率)
→ 同時確率密度関数: P(a ≤ X < b, c ≤ Y < d) = ∫ab∫cdf(x, y)dxdy f(x, y) = 1/2πσ1σ2·√(1 – ρ2)· exp[–1/2(1 – ρ2){((x – μ1)/σ1)2 – 2ρ(x – μ1)/σ1)(y – μ2)/σ2)}] Def. E(X) := μ1, E(Y) := μ2 → XとYの共分散 covariance , cov(X, Y)cov(X, Y) = E{X – E(X)}{Y – E(Y)} Cp. sxy = 1/nΣi=1n(xi – mx)(yi – my)
cov(X, Y): discrete = Σi=1n(xi – μ1)(yi – μ2) (Cf. 級内相関 intraclass correlation) Th. 共分散の性質
1) cov(X, Y) = E(XY) – E(X)E(Y) = E{XY - XE(Y) - E(X)Y + E(X)E(Y)} ___2) cov(X, Y) = E(XY) – E(X)E(Y)= E(X)E(Y) – E(X)E(Y) = 0 [期待値の性質より] 確率楕円と信頼楕円 density ellipse and confidential ellipse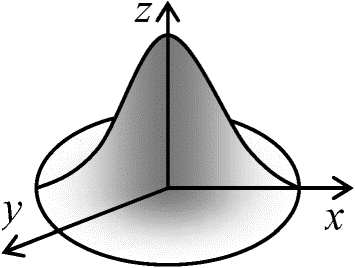
正規分布曲面 z:
z = φ(x, y) = 1/(2π√(1 – r2))· exp{–(x2 – 2rxy + y2)/(2(1 – r)2)} r: correlation coefficient between x and y → μx = μy = 0, σx = σy = 1 max(z) = φ(0, 0) = 1/(2π√(1 – r2))→ a) rによってzの最大値が決まる z = ∃c (0 < c ≤ 1/(2π√(1 – r2)))→ c = φ(0, 0)·exp{–(x2 – 2rxy + y2)/(2(1 – r2)}
x2 – 2rxy + y2 = –2(1 – r2)log{c/φ(0, 0)},
x = ξcos(π/2) – ηsin(π/2) = 1/√2·(ξ – η), ∴ ξ/(1 + r)2 + η/(1 – r)2 = 1 → 楕円の標準形 a = 1 + r, b = 1 – r → ξ/a2 + η/b2 = 1 → 扁平度, b/a = (1 – r)/(1 + r) → b) rから確率楕円扁平度定まる → a) b)より(確率)楕円確定 //Def. 信頼度αの信頼楕円(集中楕円 ellipse of concentration) x2 – 2rxy + y2 = (1 – r2)/k2 → P((x, y) ∈ D) = α ∫∫Dχ(x, y)dxdy = α, χ2 := (x2 – 2rxy + y2)/(1 – r2)→ P(x2 – 2rxy + y2 ≤ (1 – r2)/k2) = P(χ2 ≤ k2) = α ポアソン回帰 poisson regression (event count model)コックスの比例ハザードモデルと密接な関連
従属変数 = ポアソン変量 ゼロ膨張ポアソン回帰 zero inflated poisson regressionzero inflation: 0になる原因が複数存在 → ポアソン分布で算出される理論値より0多くなる→ 過(剰)分散 overdispersion の原因 1) Y = 0となる確率 → ロジスティック回帰 → P(y = 0) = p + (1 – p)·e-λ2) Y = kとなる確率 → P(y = k) = (1 – p)·e-λ·λk/k! 3) pとλをモデル化
p: ロジスティック回帰 → logit(p) = Gr, or p = 1/(1 + e-Gγ) |
|
(岡田 1980) 1) 回帰平面方程式回帰直線(2次元)を回帰平面(3次元)に拡張 f(x, y, z) = [(x, y) → z]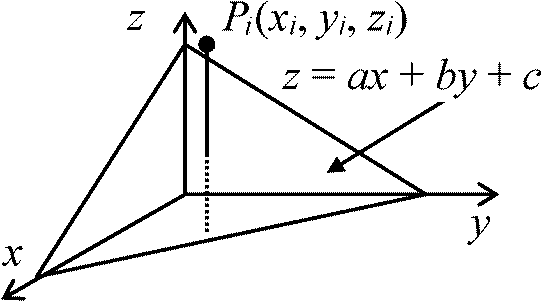 平面 z = ax + by + cの回りのzの分散, w w (= sx2·xy) = 1/n·Σi=1n{zi – (axi + byi + c)}2 … (1) Min(a, b, c)が平面方程式の解→ ∂w/∂a = 0, ∂w/∂b = 0, ∂w/∂c = 0 → a, b, c求まる ∂w/∂c = 1/nΣi=1n2{zi – (axi + byi + c)}( –1) – c = 0mx = 1/nΣi=1nxi, my= 1/nΣi=1nyi, mz = 1/nΣi=1nzi ∴ c = mz – amx - bmy … (2) (2)を(1)に代入 w = 1/n·Σi=1n{(zi – mz) – a(xi – mx) – b(yi – my)}2 ∂w/∂a = 1/nΣi=1n2{(zi – mz) – a(xi – mx) – b(yi – my)}{–(xi – mx)} ∂w/∂b = 1/nΣi=1n2{(zi – mz) – a(xi – mx) – b(yi – my)}{–(yi – my)} 分散: sx2 = 1/nΣi=1n(xi – mx)2, sy2 = 1/nΣi=1n(yi – my)2, sz2 = 1/nΣi=1n(zi – mz)2 共分散: sxy = syx = 1/nΣi=1n(xi – mx)(yi – my),
___syz = szy = 1/nΣi=1n(yi – my)(zi – mz), ∴ a =  ∴ z =  ·y + c
⇒ (x, y)の上のzの回帰平面, or z = mz + a(x – mx) + b(y – my)→ 最良1次推定関数: 同様4次元以上にも拡張可能 → > 3次元: 視覚的に理解しがたい(グラフ理論) 2) アンドリュース・プロット Andrews plot3) 重回帰 (multiple regression)y = b1x1 + b2x2 + … + bnxn + b0
y: 回帰推定値 b0: 誤差項 Def. r (重相関係数 multiple correlation coefficient)= {Σ(yi – my)(yi^ - my)}/{√Σ(yi – my)2Σ(yi^ - my)2} Def.. 寄与率 proportion (決定係数), r2
= Σ(yi^ – yavg)2/√{Σ(yi - yavg)Σ(yi^ – yavg)}2 (⇒ Σ(yi – yavg)(y^ – yavg) = Σ(yi^ – yavg)2) r2/(1 – r2)·(n – p – 1)/p
= (sr/syy)/[(syy – sr)/syy]·(n – p – 1)/p Yi: 実測値yiをx1を除くx2, …, xnからの予測値 predicted values → 予測誤差 prediction error, ui = yi – Yi X1i: 実測値x1iに対しx2, … , xnからの予測値 → 予測誤差, vi = x1i – X1i → 変量uとvの相関係数 = 「x2, …, xnの影響を除いたyとx1の偏相関係数」(記号 ry1·2…n)
→ 見かけ上の相関: 変量yとx1間に本来相関関係ないが相関得られる → 見かけ上yとx1の間に相関関係があるように見える Ex. 小学校全学年児童: 身長(y)-成績(x1)関係 → 「身長-成績間に正の相関」変量年齢(x2)を考え、この影響を除いた偏相関係数を計算すると身長-成績間相関は消える |
Def. n次偏相関: n個の制御変数のときの偏相関
Ex. 1次偏相関 first-oder partial correlation, 単回帰 r = 0次
= 1 – (SE/(n – p – 1))/(ST/(n – 1)) 残差分析: てこ(梃)比 leverage 重回帰と他解析との関係説明変数 = 名義尺度 ≡ 分散分析や数量化I類説明変数 = 名義尺度/計量尺度混在 ≡ 共分散分析 被説明変数 = 名義尺度 ≡ (線形)判別分析 多重共線性(マルチコ) multicollineality共線性 collinearity: 複数点が同一線上に存在 → 線形回帰モデルに影響説明変数多 → 残差平方和小 → 重相関係数大 / → 偏回帰係数の分散大 → 安定性少 説明変数↑ = モデル推定値と実測値の(重)相関係数↑説明変数間に(強い)相関 → 回帰係数推定値の分散大きくなり変数推定結果不安定 (多重共線性) Ex. y = a1x1 + a2x2 + a3, x2 = bx1 [x1-x2に高い相関]
→ y = a1x1 + a2(bx1) + a3 = (a1 + a2b)x1 + a3
1) 理論的基盤 → 独立変数選択 リッジ回帰ridge regression (RR)多重共線性対処にリッジ回帰定数を組入れ回帰係数安定性高めるシュリンケージ法 shrinkage method: 回帰係数安定推定が通常最小2乗法で得られない時使用
定数(λ)を相関行列対角線に加え、相関行列は全対角要素を1に再標準化(非対角要素は定数で割る) (Box & Jenkins 1976, Sokal & Rohlf 1995) 自己相関 autocorrelationDef. 自己相関: k個観測値をずらしたときの自分自身との相関 self-similarity of variates adjacent in space or timeCase. 1次元(時間) → 前向き予測/後向き予測 Def. 自己回帰 autoregression: 自己相関を持つ系列を逐次的に決定する構造 – 通常回帰に還元X(μ, σ) → 観測間隔tにおける値をX(t) (仮定: tは離散型整数値) H: 確率変数X(t)は値X(t - 1)との間に二次元正規分布構造 → 標準化 x(t) = (x(t) – μ)/σ ~ N(0, 1) → x(t) = rk·x(t - 1) + u, u = z(1 - rk2)1/2, z ~ N(0, 1), tに独立→ 一階自己回帰過程 autoregressive process 標準形 Def. 一期(一階)自己相関係数 autocorrelation coefficient, rk: -1 ≤ rk ≤ 1 観測されるX(t)について書き直す (X(t) - μ)/σ = rk[X(t - 1) - μ]/σ + u → X(t) = (1 - rk)μ + rk·X(t - 1) + σu X(t) = (1 - rk)μ + rk·X(t - 1) + U, U = zσ(1 - rk2)1/2 Y = α + βX + U の特殊ケース → Y = X(t), X = X(t - 1), α = (1 - rk)μ, β = rk, U = zσ(1 - rk2)1/2 ~ N(0, σU = σ(1 - rk2)1/2
→ rk = β, μ = α/ (1 - β), σ = σU/(1 - β2)1/2
SE(rk) = √{(1/N)(1 + 2Σri2)}, i = 1, 2 …, k – 1 (N: 系列内の観測値数) 仮定: 全自己相関 = 0 → 標準誤差(rk) = √{(1/N)(N – k)/(N + 2)} Def. ホワイトノイズ標準誤差: ボックス-リュングのQ, Box-Ljung static: ラグkが与えられたときQ統計量 Qk = n(n + 2)·Σ[ri2/(n - l)] for i = 1 to k 観測値が十分多いとき → Q統計量: χ2(df = k – p - q)p, qはそれぞれ自己回帰と移動平均パラメータ数 コクラン・オルコット法 Cochran-Orcutt method: 自己相関修正法Def. 偏自己相関係数 partial autocorrelation, Pm m次のPmはt - 1次前向き予測誤差 ∈ fm–1とt - 1次後向き予測誤差 ∈ bm+1の相関係数 Pm = Σi=mt–1∈fm–1(i)∈bm–1/√[Σi=mt–1{∈fm–1(i)}2{∈bm–1(i)}2] → 線形予測係数と違いモデル次数に非依存な量 rkと密接に関係しm次のPmはm次自己回帰モデルのm次自己回帰係数am(m)かbm(m)に一致rkやPmはRの逆行列で求まるが1次モデルから次数を大きくする再帰的アルゴリズム(Levinson-Durbinアルゴリズム)で1次からm次までの全rkとPmをO(m2)計算量で高速計算できる Ex. 音響特性: 声道断面積関数予測与える等の利点から音声信号処理利用 階層的重回帰分析 hierarchical multiple regression重回帰で変数投入順序に階層性を持たせたもの - データの階層性を扱っているわけではない |
回帰分析の応用 = 複数物質の生物活性を相対評価
量分反応 all or nothing response→ 従属変数二値応答 (2値データbinary data) Ex. 生存・死亡用量-反応曲線: 用量を横軸に反応を縦軸にとる曲線 → 単調増加曲線仮定 P(y = 1|x) = f(α + β1x1 + β2x2 + … + βnxn + u) = f(y*) yi = 1 if yi* > 0, or 0 if yi* ≤ 0 P(y* > 0) = P(β'x + u > 0) = P(u > -β'x) = 1 – f(-β'x) = f(β'x) 標準正規分布仮定 → f(y*) = φ(y*) → プロビットモデルロジスティック分布仮定 → f(y*) = exp(y*)/(1 + exp(y*)) → ロジットモデル
係数の意味 1. プロビット分析 probit analysisプロビット曲線 probit curve: 反応率が用量の対数に対し正規分布累積確率(正規分布関数)関係をもつ曲線= 対数正規モデル log-normal model: 対数正規確率紙に用量をx軸、Pbをy軸にプロット → 直線近似 プロビット変換 (probability unitの略) probit transformation: 不等分散性は除去されないp = r/n → 正規分布%点 ≡ プロビット(Pb) → 5を加え使用(負値を扱わない, 慣例的) Ex. 10匹中4匹死亡 → p = 0.4の正規分布%点 = -0.253 (+5 → 4.747) = プロビット probit 値 LD50: p (死亡率) = 0.5の時の用量 2. ロジスティック回帰モデルlogistic regression model= ロジット分析 logit analysisp(x) = 1/(1 + e-z), z = f(x) → L(p) = {1/(1 + ez)}p{1/(1 + ez)}(p – 1)
f(x) = -(ax + b) → 多変量に拡張 交互作用はb12x1x2とし組込む ロジスティック分布関数: pi
= ∫-∞log10di(e(x – μ)/τ/(τ(e(x – μ)/τ)2)dx 平均 = μ(–∞ < μ < +∞), 分散 = π2τ2/3 ロジット変換 (logistic unitの略) logit transformation: 2値データ変換に使用(正規性は決して表われない)Def. 対数オッズ(= ロジットlogit), x' = loge(p/(1 – p), p = 観察比率, [p = 0, 1変換できない] → –∞ ≤ x' ≤ +∞
交絡因子をモデルに取りこみ変数の影響調整
|
3. トービットモデル Tobit model
y* = x'β + uu~N(0, σ2) y = max(0, y*) P(y = 0) = P(x'β + u ≤ 0)
= P(u ≤ -x'β) a) 途中打ち切り回帰モデル censored regression model yi* = x'iβ + ui yi = (yi* if yi* > 0, or 0 if yi* ≤ 0) yi（被説明変数）が観測されない(0の場合)でもxi(説明変数)は観測される b) 切断回帰モデル truncated regression model
yi* = x'iβ + ui, yi = yi* (if yi* > 0) 4. Cochran-Armitage検定 Chochran-Armitage trend test= Cochran-Armitageの(傾向)検定外的基準が連続変数 → 各群の比率が外的基準と線形傾向があるかどうかを検定 量分反応 all or nothing response計数値データ → 多値応答 Ex. 反応割合proportion reacting(Walker & Buncan 1967, Truett et al. 1967) 多重ロジスティックモデル multiple logistic model外的基準変数: 0/1型データ→ 重回帰式予測値は負値や1以上の値をとり不適当 → (2)式ロジスティックモデル適用 = ロジットを独立変数線形結合式で表す ある事象発生確率, P(0 ≤ P ≤ 1) → P/(1 – P) = オッズ比。log(P/(1 – P)) = ロジット
log(P/(1 – P)) = b0 + b1X1 + b2X2 + … + bpXp = λ … (1) = 1/{1 + exp(–(b0 + b1X1 + b2X2 + … + bpXp))} … (2)
b0, b1, b2, …, bpは最尤法で求める Ex. 現在の疾病状態をリスクファクタ(喫煙、飲酒習慣等)で説明するのはリスク曝露期間一定でなく誤り b) 得たリスク予測は一定期間後のものEx. 5年間追跡調査による予測は5年以前以後の予測と無関連。3年後予測にはデータ調整し(Ex. 4年後死亡は3年後では生存)再度分析 c) 各変数が予測にどの程度寄与しているかの判断 → 標準化係数を見るd) 予測式は分析使用標本群で最適
→ 別群適用可能性不明 対数用量反応(直)線 log dose response line |
|
ある時点から事象eventが起こるまでの時間を分析 → [必要情報(変数)] 事象発生の有無(打ち切り問題) + 事象発生時間 考慮: 事象発生は観測より以前である 特定対象: 基準時間(T0) → 非可逆変化(死亡・発芽等)生起(T)必要時間 Ex. 術後再発時間(≈ 生存時間 s.s.) 評価指標(エンドポイント) end-point: 事象発生までの時間 time to event
→ 生存時間 survival time (s.l.)
Ex. tまでの累積死亡割合 → pdf. T = f(t)
打切標本 censored data生存時間は、生存時間が打切り時間より長いという情報のみ = 正確生存時間未知 Ex. 「肺癌発症」と「心疾患による死亡」 → 片方の事象が発生するともう一方は観測されない A) パラメトリックモデル→ 正規分布仮定(成り立たないこと多)生存関数 survival function, S(t) = Pr(T > t) = 1 – F(t) → tまでの生存確率 リスク集合 risk set: 時点tiでの事象未発生数と発生数を含めた全体 ハザード関数 hazard function, λ(t) = f(t)/(1 – F(t)): 瞬間(発芽・死亡)発生率
寄与危険度 attributable proportion: 罹患率(死亡率等)の差。要因暴露による対象疾病の観察集団内変化量 生存時間モデル
B) ノンパラメトリックモデル1. カプラン・マイヤーKaplan-Meier曲線, S(t)= 積極限推定量 product limit estimator 各事象発生時点での生存時間推定値 → 打切発生時点特定できる時に使用 S(t) = (1 – d1/n1) × (1 – d2/n2) × … = Πti<t(1 – di/ni), (Π product)
= (コックスの)比例ハザードモデル Cox's proportional hazards models 寿命データモデル life data model: 生存時間考慮し説明変数の生死への影響分析 ハザード比 hazard rate (Barlow 1996), hr
=(期間単位時間あたり死亡数)/(期間中間点での生存ケース数) |
3. 生命表解析 life table analysis (生命表検定life table test) 官庁統計等大規模データ使用(Greenwood): 打切時点未詳の時利用 拡張: 単位時間毎に単位期間を越え生存する確率を求め積算し生存率求める 有効観察症例, Ni = Li – wi/2 (打切が期間の真中で起こった場合)
i: 時間i – 1とi間の期間
→ 累積生存率 Si = p1 × p2 × … × pi
SiA, SiB, H: z0 = |SiA – SiB|/√{V(SiA) + V(SiB)}~N(0, 1) 生存関数検定= ノンパラメトリック [必要条件]ログランク検定 log-rank test= Cox-Mantel-Haenszel test, Peto-Peto test2本の生存曲線(f(t), g(t))を比較
H0: f(t) = g(t) 生存率曲線の差の検定 test for equality-of-survival functionM-H test: 個々の生存時間で2 × 2表作成→ 結合し全体生存カーブ有意差検討 ブレスロー-デイ検定 Breslow-Day test: n個の2 × 2分割表の解析タローン・ウェア検定 Tarone-Ware test階層データ一般化ウィルコクソン検定 generalized Wilcoxon test後期生起事象を重く評価 (Mantel 1967)打ち切り例のない場合 → Wilcoxon検定 → 拡張 固定効果fixed effectと変量効果random effectEx. 携帯における送信メール文字数は送る相手の親密度、送信者により変化「あなた」が「親しい友人」に「明日の予定を聞く」場合でも状況によりメール長は異なる → データ(送信メール長) = 複数効果 + 相互作用 + 誤差2種類の効果 = 固定効果 fixed effect + 変量効果 random effect 固定効果 fixed effect: その因子に対し有限個の水準を想定し、それらは研究で評価したい全ての水準を含むEx. 性差: 男女という有限個(2個)水準 = 固定 (固定効果真値は定数) 変量効果 random effect: その因子に対し無限個の水準(水準の母集団)想定
→ 研究で検討する水準は母集団からの標本 性差実験: 性別は全実験で男女両方採る(= 固定効果)が、被験者は(経時データでない限り)異なる(= 変量効果) Ex. 関心個々人 = 対象特定の人 → 被験者効果 = 固定効果 ≠ 変量効果⇒ 固定か変量かは解釈で決まる = 決まっているものではない 今後の課題一般的総説: 複数文献紹介し特定結論提示 – 客観性乏しく意見止まり多[バイアス = 独断偏見] 他研究者が同文献参考 ×同結論となる保証なし 系統的総説(概説) overview: [原則] 別研究者が同手続きをとれば殆ど同結論を得られる客観性の高い総説明確な目標、文献選択方針、それらの質の評価システム、結果を結合する客観的方法が必要 |
|
時系列が与えられた場合の変量について分析 = 時系列time series: 変量(= 時系列データtime series data)を時間順に並べたもので、ある変量の時間的推移 経時測定データ repeated measurement or measures 時系列表示 (Malinvaud 1970)
時間軸 time profileグラフ 1. 時系列データの時間要素に関わる特性の分析全般 (s.l.)定常過程 stationary process: 平均値 → 測定時間伸ばすと徐々に安定定常時系列 stationary series, Pr(t)
定常性 stationary → 時間により決定 – 大変動伴うものに適用不可 b) 等比級数法 geometric progression: yn = y0(1 + r)n, r = t√(y0/yt) – 1 c) 放物線: y = atb, or logy = loga + blogt → Y = A + bT: 一次式に還元 d) 修正指数曲線: y = K - abt, or log(K - y) = loga + tlogb e) ロジスティック曲線 logistic curve:
yt = K/(1 + meat), or 1/yt = 1/K + m/K·e-at
Ex. x = 年齢 vs y = 死亡率の対数 → 成人後は直線関係
m(t) = 年齢tでの死亡率,
A0 = 傾き,
Gt = 年齢, 2. スペクトル分析 spectrum or spectral analysis (s.s.)時間の遅れ(ラグ lag)の検討が必要 → 交差相関cross correlation時系列データと時間変動の特性 循環変動と固有値解析 不規則変動と時系列モデル不規則変動解析 → スペクトル解析と相関分析が応用された
スペクトル解析: 不規則変動を各周波数の合成波と考え、各周波数成分の重要度等を分析
→ y(t)とy(t – m)間相関を調べ検出 → スペクトル解析と相関分析はフーリエ変換を通じ相互に等価 変動特性解析 trend analysis
加法: X(t) = T(t) + C(t) + S(t) + I(t) ⇑ 循環変動、季節変動は一定 乗法: X(t) = T(t) × C(t) × S(t) × I(t) ⇑ トレンド推移に伴って循環変動、季節変動は変化 - 一般的 |
0) トレンド分析 trend analysis
トレンド関数 trend function: 単調傾向 monotonic trend b) αeβt: 指数トレンド → 指数平滑化法 exponetial smoothing c) K/(1 + αe-βt): ロジスティックトレンド 時系列Y(t)標本データ使用
→ Y(t)を(離散的)時刻tで回帰分析 単純モデル → y = f(t): 線形関数(非線形関数使用もある)
トレンド分析は比較的単純な分析から得られる テクニカル分析・罫線分析: 局所的最大(小)値予測に関心ある場合、極値のみを使用しトレンド分析 t: 期、(b1 … bp), (b1 … bq): パラメータ, u: ホワイトノイズ white noise →1) 自己回帰モデル auto-regressive model, AR model, AR(p)
分析対象時系列Y(t)が循環的変動する場合は、直線的トレンド分析は明らかに不適当 Yt = μ + u + b1ut–1 + b2ut–2 + … + bqut–q 3) 混合モデルa) 自己回帰移動平均モデル = autoregressive moving average, ARMA
ARMA(p, q) = autoregressive integrated moving average, ARIMA
ARIMA(p, d, q) = autoregressive conditional heteroscedasticity, ARCH d)一般化自己回帰条件付き分散モデル = generalized autoregressive conditional heteroscedasticity, GARCH 他に扱う変数を多変量に拡張したモデル vector autoregressive, VAR等 トレンド検定(傾向検定) trend test: 時間経過(暴露量増加)に伴う反応変化を検定自己共分散: プライス・ウィンステン法 Prais-Winsten method (Prais & Winsten 1954): 時系列データ自己相関修正法 コックス・スチュアート検定 Cox and Stuart's test: トレンド解析に用いる ゆらぎ fluctuationDef. ある量(Ex. エネルギー、密度)の平均値からの変動二乗平均ゆらぎ (= 分散) 分類: スペクトル密度(パワースペクトル密度 power spectral density)による
1/f0ゆらぎ(→ ホワイトノイズ): 完全にランダムで予測不能 |
変数選択法: 最良予測変数 best predictor を選ぶ方法 (オッカムの剃刀)
0) ステップワイズ法 stepwise methodF-値 (F-value) → 独立変数追加・除去基準: 各変数偏F値によるFin，Fout
→ 有意確率換算 Pin，Pout
→ 有意水準α%で棄却 → モデルに変数加える F値 < Fout値: それぞれの変数のt値を2乗した統計量 → モデルから変数削除
経験的には、どちらも2.0にするのが良い Def. 報量基準 information criterion: モデル良否の指標 1) 赤池情報量基準 AIC method (Akaike’s information criterion)モデル相対評価 → 真のモデルを当てるものではないAIC = –2·logea^ + 2p,
logea^: 最大対数尤度 D = null model → 最大逸脱度 ⇔ D = full model → 最小逸脱度 a^2↓ [モデルのデータへの当てはまりのよさ] → AIC↓p↑ [モデルの複雑さ] → AIC↑
∴ logea^とpのバランスでよりよいモデル決まる b) シーピー統計量 Cp statistic (Mallows's Cp statistic) Cp = Se/σ2 + 2(p + 1) – n: 小 → 良いモデル |
c) ベイズ情報量基準 Bayesian Information Criterion, BIC = シュワルツのベイズ情報量基準 Schwarz's Bayesian Information Criterion (1978) BIC = -2·loga^ + logn·p, n: サンプル数 BIC↓ ⇒ モデル適合度↑ (AICと同じ) AICと比較: 選択は一致性標本数多 → 真の次数に近づく + 母数少ないモデル選択傾向 2) 予測平方和 predicted sum of square, PSSPSS = Σi=1n(ei/(1 – c)): 小 → 良いモデル
c: 関数hatによって計算されるモデルの変数で回帰した時のレベレッジ 1/cは「そのサンプルの予測値推定に実質的に使用したサンプル数」とも考えらる。Ex. レベレッジ = 0.9のサンプルでは、そのサンプルの予測値はそのサンプル自身でほとんど決定されている 3) カルバック-ライブラー情報量 Kullback-Leibler information= K-L情報量, カルバック情報量真の確率分布密度p(y)と推定確率分布密度q(y)のずれ → p(y)からq(y)分布が得られる確率の逆数 I(p, q) = ∫p(y)·ln(p(y)/q(y))dy = Σi=1np(yi)ln(p(yi)/q(yi)) → I(p, q) ≥ 0, p(y) = q(y) → I(p, q) = 0 –I(p, q) ≡ 負のエントロピーEx. 勝率予想: ある球団の勝つ確率 予測A = 7割: pA = (0.7, 0.3) ↔ 予測B = 5割: pB = (0.5, 0.5) → 実際の結果 = 勝率6割: q = (0.6, 0.4)
I(q, pA) = 0.6ln(0.6/0.7) + 0.4ln(0.4/0.3) = 0.0226 = Σi=1nqilog(1/qi) = H(p0) – I(q, p0), H(p0) = logn, p0 = (1/n, …, 1/n) I(p, q) = Σi=1np(yi)ln(p(yi)/q(yi)) = Σi=1np(yi)lnp(yi) –Σi=1np(yi)lnq(yi)
第1項は定数となる → 第2項を大きくするモデルが良い 4) minimum description length, MDLデータを最も圧縮できるモデルが最良5) cross validation (別掲)6) final prediction error, FPE |
一般化線形モデル (generalized linear model, GLM)Y = a + bX → 独立変数の質問わない [ただし線形]Y ~ P(f(X)) → 指数関数族確率分布(正規分布・2項分布・ポアソン分布等)のバラツキを見る 連続型因子(変数)に拡張可 → 実験計画内に共変量とし取り込む 最尤推定によりパラメータ決定過分散 overdispersion分散変数 dispersion parameter, φ: 確率分布ごとに想定された値Ex. 正規分布 φ = σ2, 二項分布/ポアソン分布 φ = 1 |
一般化線形混合モデル (generalized linear mixed model, GLMM)GLMにおいて変量効果 random effect を考慮変量効果 → 擬似反復 pseudo-replication 避けられる Ex. 個体A = 10データ + 個体B = 5データ → 15個プールした分析は誤り(データ独立性保たれない) → 個体 = ランダム要因 → 個体差を統制した上で固定効果調べられる |
演習 (practice)N(0, 1), ∫02.45φ(t)dt = 0.492 (df = 9)の分布で∫-2.262.26φ(t)dt = 0.95。φ(t) → その分布の確率密度関数pdf1) 銅貨を100回投げる時、表の出る確率をXとする。X/100の平均値と標準偏差を求めよ。 表の出る確率 p = 1/2 裏の出る確率 q =1/2, X~B(100, 1/2)
∴ E(X) = np = 100·1/2 = 50, V(X) = nqp = 100･1/2･1/2 = 25
P(x ≥ x0) = P{t ≥ (x0 - 75)/15} = 0.2 limn→p{Yn2 ≤ n + √(2nx) = 1/√(2π)} = 1/√(2π) ∫-∞xet^2/2dt 成立を中心極限定理から示せ(E(Xi4) = 3は既知) Xi~N(0,1) → E(Xi) = 0, V(Xi) = 1, V(Xi) = E(Xi2) - E(Xi)2 ⇒ E(Yn2) = E(X12 + X22 + …+ Xn2) = E(X12) + E(X22) + … + E(Xn2) = n V(Yn2) = V(X12 + X22 + … + Xn2) = V(X12) + V(X22)+ … + V(Xn2) = 3 - 1 … (1) 中心極限定理によりYn2 ≈ N(n, 2n), or (Yn2 - n)/ √2n ≈ N(0, 1)∴ limn→∞{Y ≤ n + √(2nx)} = limn→∞{(Yn - n)/√(2nx) ≤ x} ≈ ∫-∞xφ(t)dt = 1/√(2π)∫-∞xe-t^2/2dt 4) 一様分布U(α, β)に従う確率変数Xの平均値E(X)と分散σ2(X)を求めよ From def., E(X) = ∫-∞∞xf(x)dx = ∫αβ[1/(β - α)]xdx= 1/(β - α)·∫αβxdx = (β2 - α2)/[2·(β - α)] = (β - α)/2 E(X2) = ∫-∞∞x2f(x)dx = ∫αβ[1/(β - α)]x2dx = (β3 - α3)/[3·(β - α)]= 1/3·(α2 + αβ + β2) σ2(X) = E(X2) - E(X2) = (α2 + αβ + β2)/3 - [(α + β)/2]2 = 1/12·(β - α)25) 連続的変量値を測定し整数位まで測定値が得られた時、測定値はU(-0.5, 0.5)に従う測定誤差が伴うとする。測定を50回行い合計算出時、その合計値に伴う誤差(ei)の絶対値が5を越す確率を中心極限定理から求めよ。50個の誤差を表わす確率度数は互いに独立 ei = X1, X2, …, X50, S = X1 + X2 + … + X50 → E(Xi) = 0, σ2(Xi) = 1/12 ∴ E(S) = 0, σ2(S) = 1/12·50 = 25/6 CLT → (S - E(S))/σ2(S) = (√6)/5 ≈ N(0, 1) P{S ≤ 5} = P{-5 ≤ S ≤ 5} = P{-5·(√6)/5 ≤ (√6)/5S ≤ 5·(√6)/5}
= P{√6 ≤ (√6)/5S ≤ √6} ≈ 2∫0√6 ≈ 2.45φ(t)dt
新型電気炉を設置し製造したカーバイドについてアセチレン発生量調査 σ2 = 1/10·Σi=110(xi - 16)2 = 1/10·(0 +0 +1 +4 +9 +1 +9 +4 +1 +1) = 3 H: μ = 15 → df = 10 -1 = 9 (one-sided)
D0.05 = p{|t| > 2.26} = 1 -∫-2.262.26φ(t)dt = 0.25 → Accept H (= 多いといえない) 修士課程生態環境科学専攻入試問題(1996)General statistics (一般統計学)1. 以下の検定は差と傾向のどちらの検定に用いられるかa. 分散分析. b. カイ二乗検定. c. 回帰. d. マンホイットニーのU検定 2. ある研究者が、スズメの雛が親から餌をもらう回数と体重増加の関係を調べた。その結果、雛が親から餌をもらう回数と体重増加には有意な正の相関があることを発見した(r2= +0.624, n = 122, P < 0.01)。このことからどのような結論が導けるか。3. 下図a)およびb)の結果から、(1)-(2)の考察が導かれた。これらの検定手法および考察は正しいか。また、誤っている場合には、その理由を述べよ。
a) 塩分摂取量には地域差があるため、脳卒中による死亡率にも地域差が生じる。 修士課程生態環境科学専攻入試問題(1997)一般統計学1. 次のa-eにおいて2つの特性の違いを簡潔に説明しなさい。
a. 母集団と標本集団
a. 2集団間の身長の違いを調べたい。標本抽出をくじ引きをもとに行い、おのおの10サンプルを採取し、t検定を用いて行った。 4. 検定を行う場合に第一の過誤(type I error)と第二の過誤(type II error)は、一般にどちらを避けるべきか。具体的な例をあげて説明しなさい。 修士課程生態環境科学専攻入試問題(1998, 前期)一般統計学 (Statistics)1. 5桁の宝くじを2枚買うとする。あなたならどのように宝くじを買うか(以下の番号から選んでもよい)。またその理由を述べよ。番号: 11111, 22222, 12345, 98765, 70531, 17896 |
2. 統計学における正規性の重要性を説明しなさい。具体例をあげて説明してもよい。 3. ピアソンの積率相関係数をr 、スピアマンの順位相関係数をsとしたとき、以下の3つの図に示されるデータから計算されるr, sについてa-cの問に答えよ。なお、図中の点線はX-Y間のおおまかな傾向を結んだ線にすぎないことに注意せよ。
図1________________図2_______________図3
A. 一人で商う。 さて、(a)どのような調査を行い、(b)どのような分析を行い、(c)どのような結果を得たら、屋台を開く候補地とすることができるのか答えよ。ただし、各々の場所において、通行人の中でたこ焼を買う人の割合は等しいと仮定する。 (d) この調査は、ある意味において現在の結果から未来を予測するモデルと捉えることができる。このモデルの欠点を列挙せよ。「たこ焼」屋を例に用いてもよい。 修士課程生態環境科学専攻入試問題(2000前期)一般統計学 (Statistics)問1. A-Cの説明にあたる適切な用語を記せ。
A. 母集団のN単位に、ある順序で1 – Nの番号をつける。大きさnの標本をとるのに、最初のk単位の中から無作為に1個をとり、その後はk個おきにとってゆくような標本抽出法。
(1) 統計学において代表値として平均値を用いることが多い。平均値を用いる利点を3つあげ、それぞれについて説明せよ。 問 4. ある薬品の副作用が問題になったとき、その薬品の副作用が許容水準を越えているかどうかを知りたい。この帰無仮説を設定し、第1種、第2種の誤りがどのような意味を持つか説明せよ。また、いずれの誤りの方が深刻か、その理由を述べよ。 修士課程生態環境科学専攻入試問題 (2001年前期)一般統計学 (Statistics)問1. A-Dについて、それぞれ2用語の意味の違いがわかるように説明せよ。
A. 「標準偏差」と「標準誤差」
サンプル
pH
この畑土壌で土壌が採取された時点での平均pHを求めたいが、サンプル3の7.2という値が気になる。どのように対処すべきか。 問 3. ある地域における脳卒中発生率と所得の度数分布表を作成し、この2変量間でスピアマンの順位相関係数を求めたところと有意な正の相関があることがわかった。このことから、「この地域において高所得者は脳卒中が発生しやすい」と結論づけることができるか。まず、「できる」、「できない」を明示し、次に、その理由を述べよ。問 4. 表は、あるプロ野球選手の1996年から2000年までの試合数、打率、本塁打数、打点を示している。
出場
この選手が、2001年もプレーすると仮定できたときの打点を予測したい。上記の表の情報だけをもとにモデルを可能したとすると、どのようなモデルが作成できるか。その原理(根拠)を説明せよ。また、作成されたモデルの予測精度はどのようにして確かめればよいか。解答には、モデルの計算結果を示す必要はない。 修士課程生態環境科学専攻入試問題(2002年前期)一般統計学 (Statistics)1. 設問A-Cについて、それぞれ答えよ。
A. 「データ」と「情報」の違いを説明せよ。
相関係数、最小2乗法、誤差、平均、標準偏差、予測、棄却、共分散
問1. 帰無仮説と対立仮説を示せ。 |
