(2025年7月21日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 種間相互作用
|
表. 二種個体群間の相互関係分類 (a/b = 種a, bの利益) (Pianka 1978)
競争 = -/-(+); 中立 0/0 双利共生 +/+ 片利共生 +/0 片害作用 -/0 食う-食われる(+ ベーツ擬態) +/- 異種個体間相互作用 (interspecific interaction)拮抗作用 [-/-, -/0 or -/+] antagonistic interaction (antagonism): 生活上少なくとも一方は害を受ける
= 片害作用 + 搾取作用 + 競争 (Clarke 1954) 相害作用 [-/-] 関係個体全てに不利な結果 Ex. 共倒れ 寄生 parasitism: (+ parasite, – host)宿主(ホスト) hostと寄生者(ゲスト、パラサイト) parasite間で寄生者が食物や空間を一方的に受けている場合
利害関係一方的 + 持続的搾取(寄生者は宿主と平衡な生存期間存在) Def. 宿主選択 host selection: 寄生者が宿主を選択すること • 外部寄生 ectoparasite (+, –): 宿主体外に寄生 労働寄生 labor parasite: PolyergusがFormica幼虫・蛹取上げ育て奴隷化 託卵寄生 blood parasite: ホトトギスがウグイスの巣に産卵 - 育てる • 内部寄生 endoparasite: 宿主内部に寄生 半内部寄生 semi-endoparasite: 一部のみ内部寄生 Ex. 寄生菌 表. ヒトに寄生する主な内部寄生虫
寄生虫名: 侵入経路-部位(中間宿主. ①第1中間宿主. ②第2中間宿主)
⇔ 単寄生 monoparasitism: 寄生者が1種 Ex. ズイムシアカタマゴバチ: コナマダラメイガ卵 - 単寄生 vs ニカメイガ卵 - 多寄生 Def. 虫癭(虫瘤) gall: 昆虫、ダニ等が植物に産卵し内部寄生 → 植物組織異常発育し瘤状に膨らむ構造
多器官(葉・茎・果実等)形成 + (特定昆虫-特定植物関係) → 色形状多様 半寄生 hemiparasitism: 宿主植物から水分・無機養分吸収
+ 糖等の炭素源は自らの光合成で獲得
卵寄生虫: 卵に寄生する昆虫 → 生物的防除に利用
全寄生植物 holoparasite: 光合成能なく全栄養分を宿主に依存 Ex. ラフレシア、ハマウツボ - 葉退化
半寄生植物 hemiparasite: 光合成能持ちつつ宿主から水・栄養分吸収 Ex. ヤドリギ: 葉緑体を持ち光合成行なう ≠ 宿主完全依存 Def. 共寄生 multiparasitism: 1宿主に複数寄生者が同時に寄生した状態共生 symbiosis (+, + or +, 0)地衣類共生の様に2種を分離すると独立生活困難となる段階から、共生関係が見られないで生活している方が多いヤドカリとイソギンチャクの例まである。一時的なものと、一生続くもの、生育のある時期にだけ見られるものがあるDef. 共同作用: 生物の助け合う関係 ⊃ 共生作用: 異種間の共同作用 双利共生 mutualism (+, +)双方の関係がなければ生きていけない結合共生: 個体間が常時接しているもの = ほとんどが双利共生
一方が他方の養分獲得上必要なある過程を補い、その物質交代を助け、他方はその養分や生活場所を得ている関係が多い
アリ植物-アリ(アリ共生 myrmecophilous)、虫媒花-花粉媒介昆虫
Ex. 熱帯産アリノストリデ: アリに棲家提供 + 植物はアリにより他昆虫害を回避 |
Ex. ヤドカリ-イソギンチャク: ヤドカリは体に合わせ殻を変える。抜殻となった巻貝殻中にゴカイ類が住み込み、ヤドカリ分泌物を得ると共に、殻掃除の役目をし3者共生とも見れる。イソギンチャクはヤドカリに運ばれ、ヤドカリはイソギンチャクを恐れる海産動物から身を守れる 片利共生commensalism (+, 0)一方の生活規模が大きく他方の寄生により影響を受けない例があり、寄生との区別が難しい (区別する必要はあるのか?)Ex. サメ-腹部着生コバンイタダキ、フジナマコ-直腸に住むカクレウオ、ケトプテルス(ゴカイの1種)の穴を利用し住むカニ 中立作用(不偏関係) neutral interaction or neutralism (0, 0)両種とも利益も損失も受けない関係Ex. 草食動物 = 食草十分な時に見られる種間関係 Ex. 一つの花で、ハナムグリ・ハナバチ・ミツバチ等が平衡して花粉や蜜を集める (アフリカ草原のジラフ・シマウマ・ダチョウは相互に敵発見に対する能力の増加と逃避信号となりあう(≈ 原共同作用) 捕食作用 predation (+, –)自然界構成上重要な食物連鎖の基礎をなす。他の拮抗作用と異なり、一方の生存のために他方の生存を許さない関係。一般に被食者は捕食者からの逃避活動を行う機能が、また捕食者は被食者の発見と捕食活動を行う機能が著しく発達している侵害作用Ex. 抗生作用: 抗生物質生産生物 →微生物成育停止 (≈ 一方的競争作用)
抗生物質生産が目立つのは放線菌だがカビにも多くの例: すみわけ habitat segregation複数種(品種・同種間でも)の個体群が時空間的に生活の場を分ける現象近縁種でも、棲息地のすみわけ、食物の食いわけ等で競争回避・共存 a. 環境要因に対する適合の相違による小麦の入った容器中にコクヌストモドキ属甲虫2種(a, b)を同数ずつ入れ、6つの異なる温度・湿度条件下で飼育する。a種は湿度高く温度高い条件下で、b種は湿度低く温度低い条件下で生き残る割合高い。種間競争力は環境条件に左右されることが多く、環境条件が周期的に変動すると生活要求の似た近縁種の共存も可能なことを示す b. 個体群間相互作用による
Ex. アパラチア山脈のサンショウウオ (Hairstone 1951) Ex. コロラド川大峡谷を挟んでネバダ側にハタリスCitellus eucurus、アリゾナ側にC. parrisiiがいて、環境要因の差というより地域の機械的境界が生活場所を区別する要因となる(Hall 1946) くいわけ: 同一場所でとる餌を変えることにより共存する場合Ex. ヒメウとカワウ Ex. フナとカワムツ Ex. 北海道標津川: 水生昆虫や水面落下昆虫等を食べるサケ科魚類3種 = オショロコマ、イワナ(アメマス)、ヤマメ(サクラマス) 3種が好む水温多少異なり、オショロコマは知床山系水源域、イワナは山地渓流から本流上流域、ヤマメは本流の中下流域を主な生息域とするが、しばしば共存する水域もある。共存域で3種食性を調べると、互いに異なった内容の食物を食べている 共進化 coevolution密接な生態的関係持つか、遺伝子相互交流のない2(以上)の集団(分類群)の共同進化(Ehrlich & Raven 1964)。相互に働く淘汰圧により一方が他方の進化に一部依存し進化 (s.l.)植物-動物(植食動物, 花粉媒介動物 pollinator)相互進化関係 (s.s. 一般的) |
|
捕食者 predator (= 天敵 natural enemy): 他方を攻撃し生命を奪う側の種
↔ 餌 prey: 生命を奪われる側の種 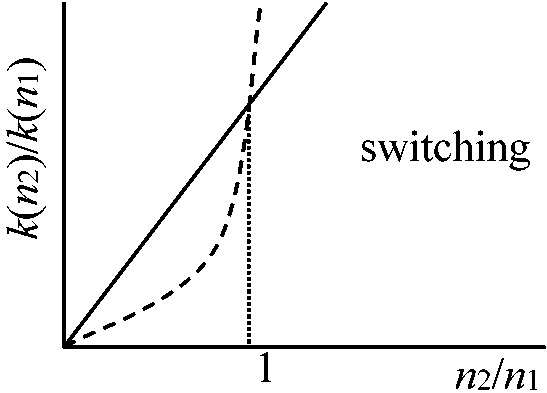
スイッチする捕食者スイッチングの要因
1. 餌個体の隠れ場所の確率
2種の餌 N1, N2 齢を考慮した捕食幼体と成体youngs (eggs) and adults: 幼体の方が捕食されやすいPopulation: young = X, adults = Y
________βY 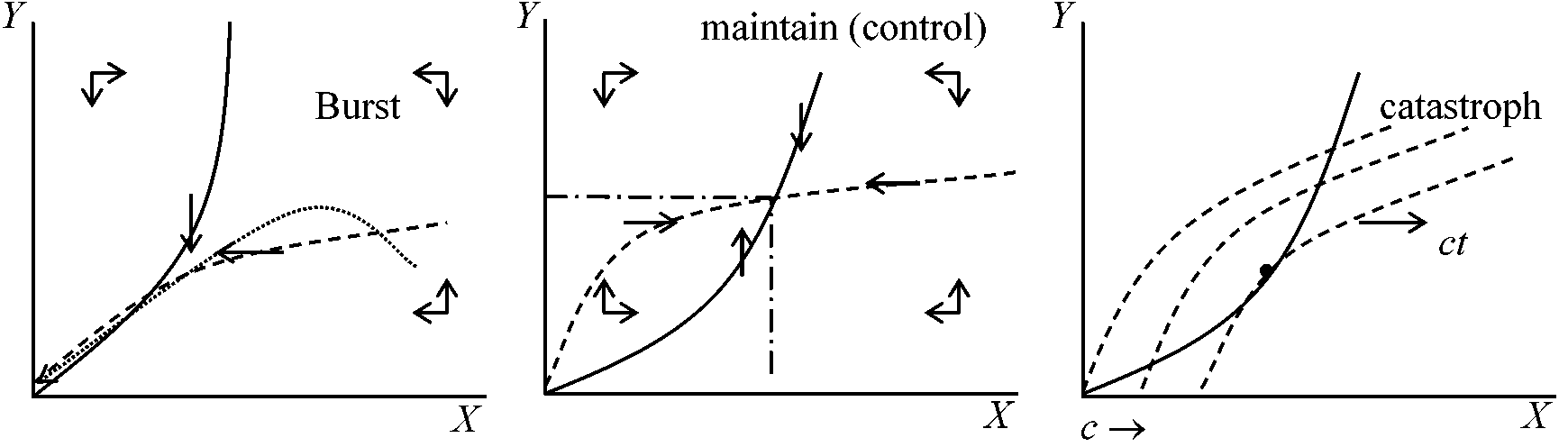
_______u(r12)
__1_____⇆_____2 u(r13) ↖↘___↗↙ u(r23) ________3
相互作用には他に共生があるが、数学モデルはあまり導入されていない(寺本1984) 食う-食われる関係 (predator-prey interactions)捕食の進化的帰結 ⇒ 共進化 = 捕食効率↑ vs 捕食回避効率↑
☛ 軍拡競争 防衛戦略 (defense strategy)一次防衛戦略(間接防衛)近くの捕食者有無に関わらず絶えず防衛 Ex. 隠遁、カムフラージュ、警告 |
Def. 擬態 mimicry: = 対象(捕食者や被捕食者)を騙すこと 隠蔽型擬態(カムフラージュ) mimesis: 隠れるための擬態
保護色(隠蔽色) protective or cryptic coloration: 背景と似た色彩 (捕食者や被捕食者両方に見られる) 警告色(標識色) warning coloration: 毒・臭・武器等有する動物 - 目立つ色彩・斑紋等 ベーツ型擬態 Batesian mimicry: 無害種が有害(不味)種に似る(含行動様式)
モデル model = 似られる方の種 ⇔ ミミック mimic = 似る方の種 近縁種間の収斂現象に限定し使用 Ex. 南米ドクチョウ群(有毒) メルテンス型擬態 Emsleyan or Mertensian mimicry
サンゴヘビ種群(南アメリカ): 18属約75種(有毒なのは1属のみ)
捕食効率を高める擬態 – 捕食者からの防御機構ではない 表. ブラジル産サンゴヘビにおけるモデルと擬態者の割合(Wickler 1968) 捕獲数 モデル仮定(捕獲個体中モデル比率) 型 猛毒種 弱毒種 猛毒性 Micrurus 214 17% モデル 17% メルテンス型擬態者 弱毒性 Erythrolamprus 906 83% 擬態者 74% モデル(ミューラー型擬態者) 無毒性 Lampropeltis 107 ┛ 9% ベーツ型擬態者 s.l. 以下のような特性も擬態に含める
化学擬態 Ex. ナゲナワグモ – 餌種(ガ)フェロモン擬似物質出し獲物誘因 二次防衛戦略(直接防衛)Ex. 隠れ家への退却、逃走、威嚇、擬死、攻撃のはぐらかし、反撃集団防衛: 集団生活生物は、その集団生活そのものが防衛目的に適うこと多 同盟防衛: 2種以上の生物が防衛関係を作る。利益は一方の種のみでもよい 植物生息地の石や土壌に色・形を似せ捕食から逃れるEx. Avonia (Portulacaceae): A. papyracea - 色や模様が石英岩に似る Ex. Lithops (Aizoaceae): 生息地の石に似る Ex. Pulmonaria officinalis (Boraginaceae) 葉の白い斑模様が鳥の糞に似る (Farmer 2014) |
|
(☛ 自然淘汰) 競争 competition
種内競争 intraspecific (intrapopulational-specific) competition資源利用均一化資源や生息場所の拡大・多様化。K-淘汰された種 種間競争 interspecific competition資源利用特定化資源や生息場所を制限。生態的分化ecological diversification (niche分割) → 個体群存続に関し正反対の影響 Solomon (1949)
機能的反応 functional response
効率良い捕食は個体群維持には賢い捕食ではない(分別ある捕食が重要) → 餌再生産を最大にする捕食 競争(的)排除則 competitive exclusion principle = ガウゼの定理 Gause's axiom, law or theorem ≡ 同じ生態的地位(ニッチ)を持つ2種は共存できない
☛ Exp. ガウゼ(Gause)の実験 種内競争と種間競争の均衡Ex. Palamecium caudatum vs P. aurelia (Gause 1934), センモウチュウ類, ショウジョウバエ, コクヌスト等, 害虫天敵と害虫の個体数の変動関係(高橋・瀬川 1983) 
_____: 害虫侵入とその後の個体数変動. _ _ _: 天敵侵入とその後の個体数変動 A, B, C: 侵入の時間間隔がA-B-Cと長くなる。D: 天敵の侵入数が多いとき。E: 安定した群集への害虫の侵入(害虫がその群集に応じる)。F: 天敵不在で薬剤防除を行う → 防除(Mutsaers 1989, 1991) 植物競争(相互作用)モデルd2Wi/dt = (d2Wi/dt)max(1 – Σjn(dWj/dt)/A)
(d2Wi/dt)max: 単一植物個体の成長率の可能性のある最大変化(つまり競争のない状態) d2W/dt2 = (1/Ru·dRu/dt)·dW/dt + Ru2W(1 – n/A·dW/dt)
Ru: その生活を通じて(d - 1)競争を除外して成長しているときの同齢植物の相対成長率 2種系数理モデル種間競争動態 intra-specific competitive dynamicsロトカ・ボルテラ式 Lotoka & Volterra(捕食方程式): 古典だが重要な式dN1/dt = r1N1(1 – (N1 + αN2)/k1) 餌種の増加率: logistic成長から餌-捕食者接触の度合いを引いたもの dN2/dt = r2N2(1 – (N2 + βN1)/k2)
N1: 餌動物の密度 N2: 捕食者動物の密度 Def. 力学系dynamics,dynamical system: 2つの微分方程式を連立 ⇒ 変形 dN1/dt = (r1 – λ1N1 – μ2N2)N1 dN2/dt = (r2 – μ1N1 – λ2N2)N2
λ1, 2: intra-specific
μ1, 2: inter-sepcific
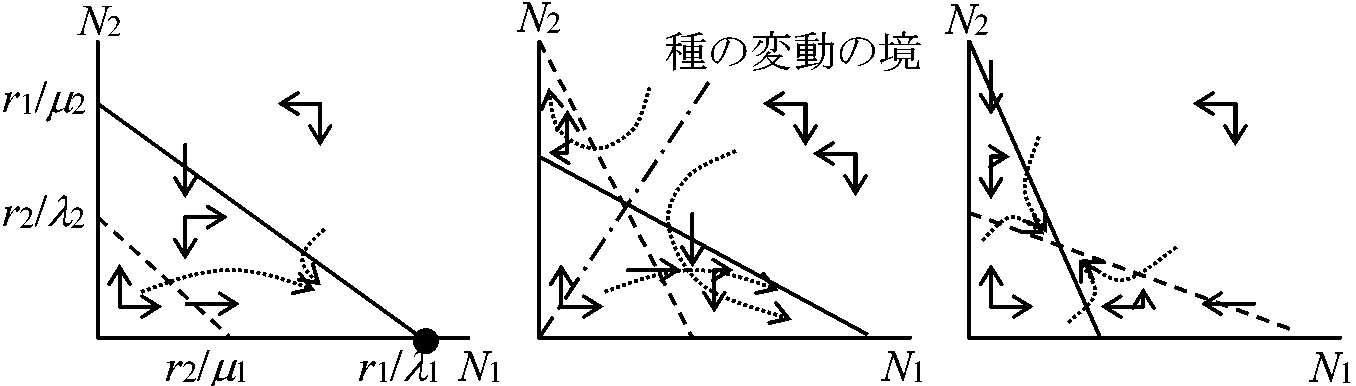
共存条件: r1 = r2 → λ1 > μ1, λ2 > μ2 ⇒ 種内競争 > 種間競争 (この意味付けはできていない) L-V式: 連続繁殖仮定(= 微分可能) ⇒ 昆虫等では世代が不連続 ⇒ 差分方程式の方がよい x0(g + 1) = R{x0(g) - x0(g)(1 - e-ay)} = Rx0(g)e-ay 有効面積 ≡ 1 - e-ay → 捕食率(または捕食寄生率) y0(g + 1) = Rx0(g) - Rx0(g + 1)
R: 世代間増加率
If y = 0 → x0(g + 1) = Rx0(g) a ≡ 寄主発見面積 area of discovery |
ホリングモデル Holling model (Holling 1959)
n = axts
n: 捕食した餌数 t = ts + hn
t: 全捕食時間 n = (axt)/(1 + ahx) ⇒ ホリングモデル 捕食数上限, n∞: x := ∞ (1/x → 0) → n [修正(拡張)式] 餌密度 x = constant → x ≠ constant LV改変モデル (Simazu et al. 1972)
LV: 餌種の密度効果がない → 組込む = 機能反応 functional response + 数的反応 numerical response エスケープ仮説 escape hypothesisEx. 周期ゼミ(≈ 17年ゼミ): 合州国北部17年、南部13年(ズレない)
17: Magicicada septendecim ↔ M. tredecim: 13 素数であることが重要か - 複数種の天敵発生の同調を回避
環境収容力の比 (k2/k1) 種が共存できる類似限界2種間競争の強さはそれらが利用する資源がどれだけ重なっているかによって大きく左右される。共通資源を利用することによって競争が生じている場合には似たものを利用する種ほど共存が難しくなる。2種の資源利用の違いをZで表わし、競争係数μ1とμ2とがzの減少関数α(z)だとする捕食圧のあるもとでの共存 coexistence under predation pressure●Predator Y⇓ ○ Sp. 1 ⇔ ○ Sp.2___k(N1) = kN1 dN1/dt = [(r1 – P) – λ1N1 – μ2N2]N1 dN2/dt = (r2 – μ1N1 – λ2N2)N2
Case 1. λ1 = λ2 = 1, μ1 = μ2 = 1/2, r1 = 3, r2 = 1 捕食者-被捕食者系 prey-predator system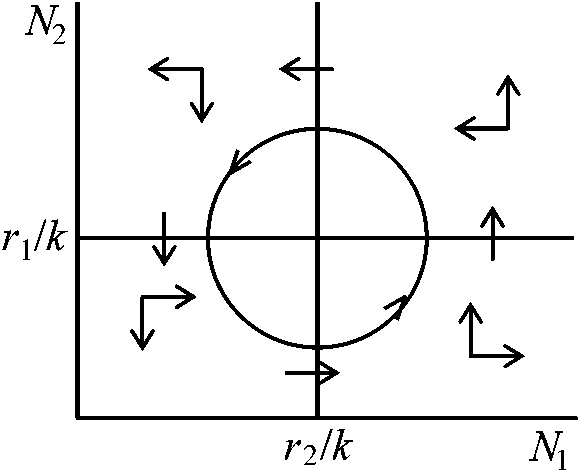 2種のprey
2種のpreydN1/dt = r1N1 – k(N1)·N2 dN2/dt = -r2N2 + k'(N1)·N2 k(N1) = kN1: Lotka-Volterra dN1/dt = (r1 – kN2)N1dN2/dt = (-r2 + k'N1)N2
⇔ limit cycle: 変動が回復しやすい(Goodwin 1951, 1967) – この系の存在が個体群維持上必要となるはず 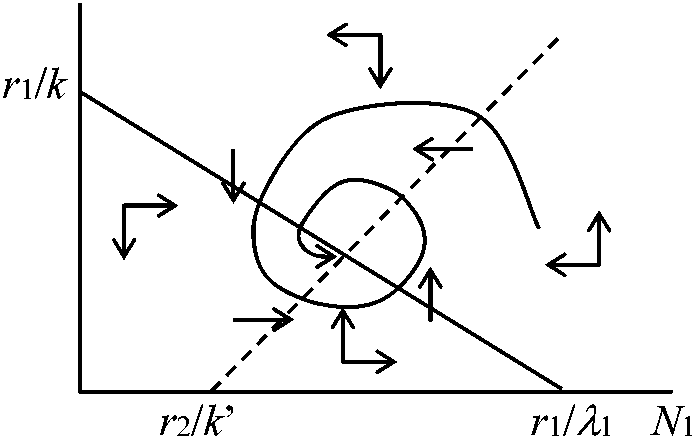 種内競争dN1/dt = (r1 – λ1N1 – kN2)N1dN2/dt = (-r1 + k'N1 – λ2N2)N2 N1 = 0 → r1 – λ1N1 – kN2 = 0 N2 = 0 → -r2 + k'N1 – λ2N2 = 0 種内競争 ⇒ 安定化 共存k(N1) = kN1/(1 + N1)dN1/dt = [r1 – λ1N1 – kN2/(1 + N1)]N1 dN2/dt = [-r2 + k'N1/(1 + N1) – λ2N2]N2 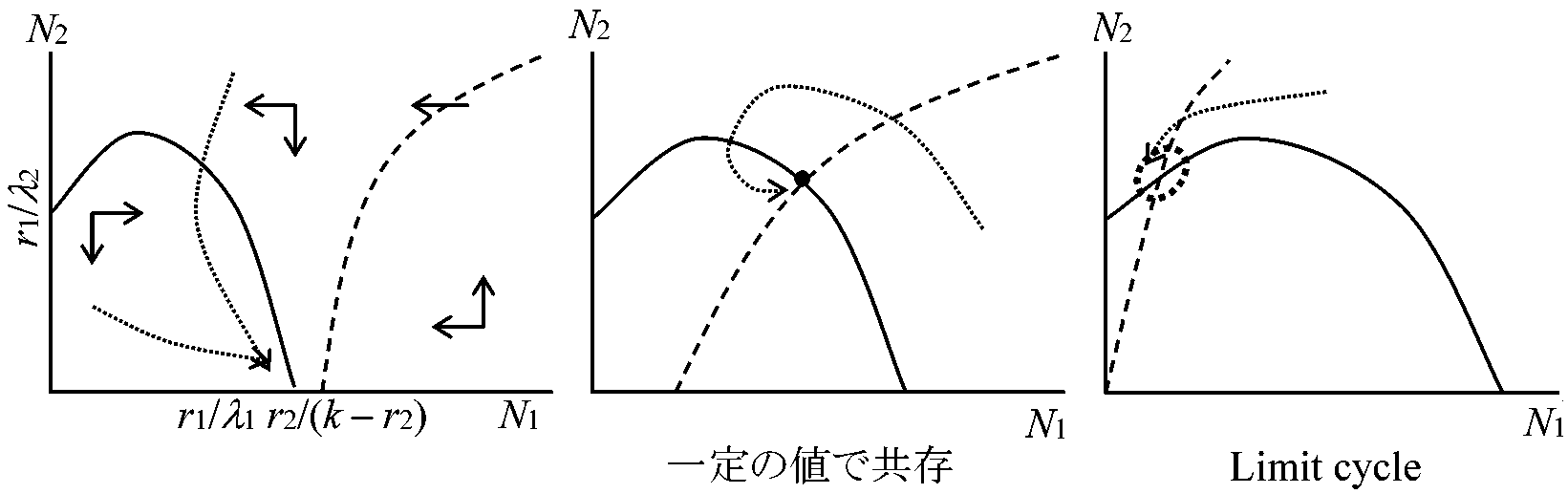 アイソクライン法変数xの増減から平衡状態とその安定性を求めることをせず、変数が2つあるので数直線の代わりにxとyを記した数平面を考えた解法。xの増加速度dx/dtの2つの領域をわける直線は:
競争実験と地理的分布陸上植物は個体サイズが大きく変動するが、xやyとして個体数ではなくバイオマスを用いることがある標高や緯度・降水量・土壌成分などが、場所によって連続的に変化する勾配(もしくはクライン)を考える。即ち、2種の動態はそれぞれの地点で競争方程式(2.1)に従い、2種の環境収容力Kとの比率、競争係数aとbなどが場所ごとに変化する。観察される種の組成はそれぞれ平衡状態にある。第1種が生息している地点から第2種がだけが生息している地点に移り変わるときに、中間地点での力学系が図のようになるならば、2種は共存を経て移り変わる 3種系1) Two-prey + One predator
___N3_______predator Volterra: k1N1, k2N2, …, k1(N1, N2), k2(N1, N2) Switching: k1(N1, N2) = k1N1/(N1 + N2)·N1, k2(N1, N2) = k2N2/(N1 + N2)·N2 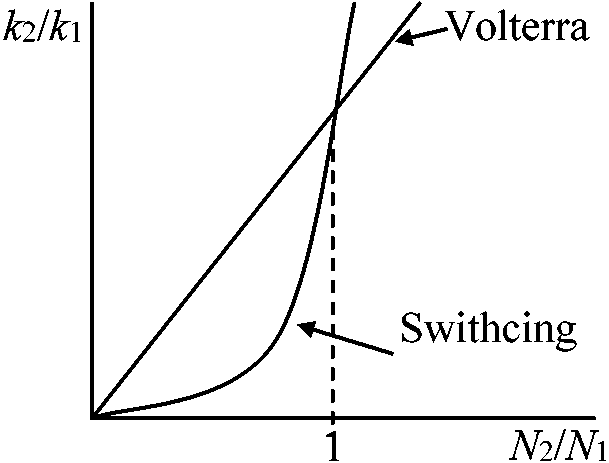 k2(N1, N2)/k1(N1, N2) = k2/k1·N2/N1
k2(N1, N2)/k1(N1, N2) = k2/k1·N2/N1k2(N1, N2)/k1(N1, N2) = k2/k1·(N2/N1)2 dN1/dt = (r1 – k1N1N3/(N1 + N2))N1 dN2/dt = (r2 – k2N2N3/(N1 + N2))N2 dN3/dt = (–r3 – (k'1N12 + k'2N22)/(N1 + N2))N3 Volterraの場合: N1とN3(or N2とN3)で周期解 Switchingの場合: 3種共存の実現 – 種間の競争のみを入れたときswitchingによって3種共存が可能になる |