(2018年1月20日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 物理学
|
法則の立場から 19世紀末以降に物理学変革期 (それ以前 = 古典物理 vs 以降 = 近代物理) 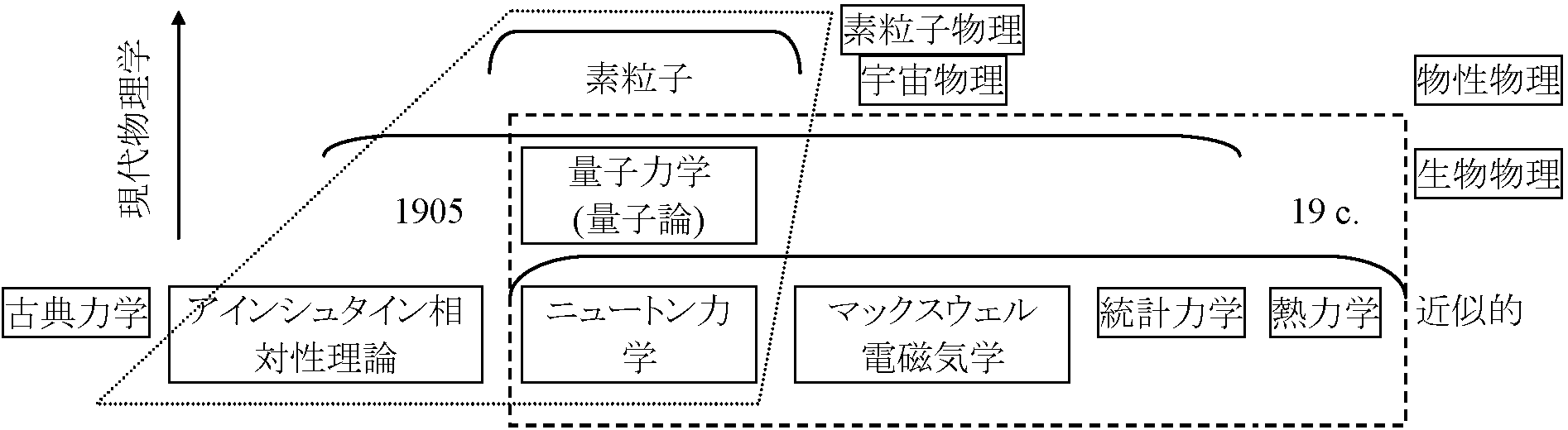
[ 宇宙 ] - 宇宙物理学 (惑星科学) [自然科学概論] 物質観 (原子論 atomic theory)物理の2つの柱: 粒子particle-原子atom → 基本的粒子, 場field原子atom: ギリシア語 ατομζ (分割されない)が語源 – 物質を形作る最小単位とした(Demokritos命名) 古代原子論: インド・ギリシアの原理論 → 独立発生インド原子論初期BC: パラマーヌ理論アヌ(微小体): 運動と結合の2力 → 空間の1点を占める → 集合 → 複合体 2 c: ウマイシェーシカ学派 地水火気の異なる4実態のアヌ → 4種集まり千差万別のものが作られる アヌの最初の力を与えたもの → 人では理解出来ない何か 6 c: プラシャスタパーダ "句義綱要"に纏める。アヌは不可分割最小単位 - 神話と決別 = 論理的発展 中国陰陽五行説構成要素ではなく、現象の特徴づけに留まる → 原子論は誕生しなかった
陰陽: 山の日陰、日当たり → 抽象原理 アラビア・フェニキア原子論9-10 c アラビア: アルアシュアリ Al-Ashari, アルラーシ Al-Raziフェニキア: モスコス Moschos → 言語の性質は原子論と関連?
アルファベット: 1音1音が構成要素、分解再構成可能 ⇔ 漢字: 分解不可 ギリシア原子論= 自然学: ギリシア哲学の重要部分 Ex. Demokritosの原子論自然的存在 → 運動・変化 = 自然界の個物を対象 / 変化した複雑な自然の統一認識 目的: × 自然研究そのもの ⇔ ○ 人が苦悩(恐怖)から免れ懸命に思慮深く生きること (Ex ギリシア神話)
現代の自然学の位置付け イオニア学派: 「万物の基礎」は何か Thales (自然科学の祖): 水 =自然中に最も多い物が自然形成の基 万物は水から生じた – 全物質はその変化と流動で生成される(バビロニア・エジプトに既に概念存在) Anaximandros: 日時計ギリシアに伝える → 時間概念 世界を構成する根源的物質は水の様な感覚できる現存物質ではない → 人間に見えない最も多量の物質 = ト・アペイロンaperion (無限のもの) Anaximenes: 根源的物質はアペリオンではなく"空気" 目に見える気体(雲等)の"気" = 自然に形として表れたものがト・アペイロン 空気濃度変化により全物質作り出される Helakleitos: 流転説 = "生成消滅" 万物流転 → 物の本質 [= 時間は永遠] 根源的物質は火(万物の起源) → 火は自然界の普遍的な流動と変化を象徴 変化: 火 → 空気 → 水 → 土 BC500- エレア学派 Parmenides: 物と運動の否定 "あるべきものはあり、ないものはない" 変化が運動のあるべき姿 – イオニア学派完成時に一時出現 Zenon: 何か目に見えぬが本質的なものは1つである Empedokles 万物の起源(不生不滅) = 火・(空)気・水・土 → これらの結合と分離により物質が生成消滅 Aristoteles: アリストテレスの4原因(4元素) 世界全体 = 2領域
我々が生きるのは月より下の世界 → 4大元素(火・空気・地・水)からなる 形相因 cansa formalis: 第一物質を規定する計画 作用因(動力因) cansa efficiens (cansa movens): 計画実現機構の準備 – 近代的”原因”概念に近い 目的因 cansa finalis: 計画される目的→ 4元素は、形相の作用で相互転化の可能性 → 原子概念否定 [錬金術 alchemy 誕生] BC420- 原子説(イオニア学派)多元化 エレア学派に対し、本質的な物は複数ありそれらは変化しないと主張 原子説: 抽象的思索に基づくが現代原子論に通じる Anaxagoras: スペルマタ説 = 万物の根源はスペルマータ spermata スペルマタ: 極微小で種類数無限 → それらの離合により万物生成 → 原子 スペルマタ + アヌ、愛と憎 Leukippos: スペルマタ説を発展 → 一元論復活 Demokritos: ギリシア原子説大成 万物は原子(atoma = 分割できないもの)という圧縮も分割もできない均質で微小な物質からなる
第1性質: 原子の属性 = 形状・大小・軽重・疎密・硬軟の5種 Epikouros: Demokritosに従う → 自然現象に不可分の物質 = 原子の運動 物質運動の場 → 物質に占められない空間 = 空虚 → 万物の本質は物質(原子)と空虚 斜傾運動 (clinamen L.): 原子は通常空間を下に向かい進むとされるが、「全く不定な時に、又不定な位置で、進路を少しそれ運動に変化を来らすと言える位なそれ方をする」 必然や運命という「むやみに恐れられる」考えを退け、我々の自由意志を確保する説明でもある 大要: ミレトスでの理論をエレア学派の人々が批判し誕生したのがギリシア原子論(= 神話的解釈との決別)
→ 目に見えないものから理解するのではなく、目に見える物から合理的・論理的に理解 原子と空虚変わらないものの離合集散で物は形作られる → 不変な物をギリシア哲学者は探しつづけたギリシア自然学の系譜
単一元素elementによる自然認識 / 生成消滅変化連動 Pythagoras: 数 = 物と物(数と数)の間には空虚が存在 → 空間 Arkithas (ピタゴラス学派): 「物体」と「物体の占める場所 = 空間」を区別 Platon: 有限な球形の宇宙が存在する無限の空間 – 等質でも等方でもない
イデアidea: 実在の最高のもの – 消滅も変化もしない Parmenides: 時間は無限の存在 Zenon: 詭弁 空間は無限小を取り得る → 運動の存在否定 → 時間は実在ではない Aristoteles原子と空虚は永遠の存在 → 消滅した物体も再生 → 循環的時間感
物質の原子的構成古代原子論と近代原子論の類似
→ 類似点: 多様性と統一性の根拠を、自然(実際)を直接見て得た論理的考察による必然的帰結 _______________________________→ 「真空」の存在 |
※ ここへの統一・到達過程が論理的に行われる必要 → 現代原子論で、原子が不可分・安定物に対し問題が出る(Ex. Proton 92まで安定 → それ以上幾つまで存在するか不明) Proton, Neutronがある数の時は安定だが、その組み合わせの元では巨大原子の形成(存在)可能性がある 自然状態下での安定度を知る事はさらに重要 誕生した課題 = 原子の発見原子 → 多様な物質(どうして多様な物質を作るのか)原子 → 熱現象(可逆的運動をする物がどうして不可逆的な物を作りえるのか) 量子法則 → 実験と論証 相対性理論への歴史電磁気学-相対性理論電磁波媒質検討 → アインシュタイン 相対性理論発表物質が高温になり電磁波や光を発する研究 → 量子力学へ発展 BC600頃 Greek 琥珀(エレクトロン)と毛皮を擦り合わせると(静電気生じ)引き合う → 電気 electolicity語源 マグネシアという所で産出される石が鉄を引きつける → 磁気magnet語源 Gilbert, William 1546-1603, 英: 物理(医者) 「電気の父」、「磁気学の父」: 近代的電気・磁気研究開始 a) 魔術・占い手段であった電気磁気現象をまとめる b) 北極に近づくと磁石が地面指す → 地球は1つの磁石 (Keplerに影響) Gray, Stephen 1666-1736, 英 静電気実験 = 物体を摩擦し導体・不導体を区別。電気流動発見 Musschenbroek, Pieter van 1692-1761, 蘭 高温計発明。ライデン瓶Leyden jarの原理を発見 1745 ライデン瓶(オランダ、ライデンの学者により発明) = 電気貯蔵装置 → キャパシタ(コンデンサー) Nollet, Abbe Jean Antoine 1700-1770, 仏: 電位計発明。ライデン瓶改良Franklin, Benjamin 1706-1790, 米: 政治家・科学者 – 凧で雷の電気をライデン瓶に導く実験(1752) Romas, Jacques de 1713-1776, 仏: 雷の実験 Aepinus, Franz Ulrich Theodor Hoch 1724-1802, 独: 蓄電器創案 18世紀 Newton力学完成 → 重力と同様に電気や磁気の力の大きさを測る試み Coulomb, Charles Augustin de 1736-1806, 仏土木工学・物理学。静電磁気学基本的法則確立 精密な測りを発明し、電気・磁気の力の大きさを測るまで技術が進む → 重力同様に力の大きさは電気・磁気量に比例し、距離の2乗に反比例 Galvani, Luigi 1737-1798, 伊: 解剖学(医学) ガルバーニの実験(1780): カエル筋肉の電気運動 2金属張合わせたピンセットで筋肉に触れると筋肉収縮 → 筋肉運動に(生物)電気関係 → Volta電池 1800 ガルバーニの実験現象 – 電気はピンセット側で作られると考えるVolta, Allessandro (1745-1827), 伊 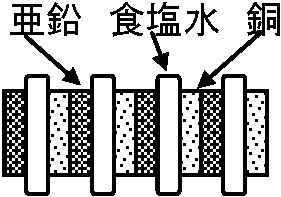 1799 ボルタの電池 Voltaic cell: 2種金属(Zn, Cu)と酸(食塩水を含む綿)を積み重ねた
1799 ボルタの電池 Voltaic cell: 2種金属(Zn, Cu)と酸(食塩水を含む綿)を積み重ねた
2種金属を酸中につけ酸の外で端を繋ぐ = 電流発生
⊖ Zn → Zn2+ + 2e-______ 電子製造
一瞬だけ得た電流を連続し流せる = 定常電流 [イオン化傾向大 ⇒ ⊖ ] 2) 電流による磁界形成発見: 電気と磁気は別現象ではなく互いに関係 Ritter, Johann Wilhelm 1776-1810: 水を電気分解 → 酸素と水素が発生 Carlisle, Anthony 1768-1840, 英: 水の電気分解 Davy, Humphry 1778-1829, 英: 電気分解で化合物形成(元素発見) → 化学的引力 = 電気的性質 Berrelius, Joens Jakob 1779-1848 各元素を静電気性と負電気性のものに分け、正負は引き合う Örsted HC 1777-1851, デンマーク: 電流が磁石に力を及ぼす(1820) → 個別に研究がなされていた電気と磁気は別々ではなく互いに関係 Ampére, André Marie 1775-1836, 仏: 物理学・数学 電流単位、アンペア(A)は彼の名 1820 アンペールの法則 Ampére's rule: 電流の流れる平行導線間に力が働く → 電流間に力が働く Biot, Jean Baptiste 1774-1862, 仏: 数学・物理学・天文学 円偏光、双軸結晶を発見 Savart, Félix 1791-1841, 仏: 医師 楽器理論。サヴァール(水晶)板、振動数測定器サヴァール車 1820 ビオー・サヴァールの法則 Biot-Savart law: 長い真直ぐな導線近傍の磁束密度は導線を流れる電流に正比例し導線からの距離に反比例 Ohm GS 1787-1854, 独: 電気抵抗概念提出 1827 オームの法則 Faraday, Michael 1791-1867, 英: 化学・物理学(電磁気学) 電気量単位、ファラデーは彼の名 1831 電磁誘導仮説: 電気磁気相互作用 → 磁界変化 → 導線輪に電圧発生
電気・磁気は周りに場を作り、その力を周りに及ぼす 1837 電磁場概念 Röhmkorff, Heinrich Daniel 1803-1877, 独: 誘導コイル発明 Lenz, Heinrich Friedrich Emil 1804-1865, 独 温度による電気抵抗の変化発見 レンツの法則 = 電磁誘導の向きに関する法則 Pouillet, Claude 1790-1868, 仏: 正弦検流計、正切検流計、日射計等発明 プイエの法則 = 抵抗含む回路の発電機起電力 = 発電機内部電流 × 外部抵抗電流 Crookes, Sir William 1832-1919, 英, 化学物理 スペクトル分析でタリウム発見、ラジオメータ(放射計)発明 1874 クルックス管考案 - 真空放電vacuum dischrge研究で陰極線直進観測 クルックス管 Crookes tube: 真空放電実験を行う、内部に陰極をもつ真空ガラス管(真空度 < 0.1 T) Maxwell, James Clerk 1831-1879, Scotland: ファラデーの場の考え受継ぐ1861 マックスウェル方程式4法則 (電磁場基本方程式)
→ ファラデーやマックスウェルの理論認められる 光学Biot, Jean Baptiste 1774-1862, 仏: 数学・物理・天文円偏光、双軸結晶を発見 Goethe, Johann Wolfgang von 1749-1832, 独: 詩人・小説家(劇作家) 色彩論、光学 → 「若きウェルテルの悩み」 – シュトゥルム・ウント・ドランク運動。ワイマールの宰相を勤めた後、イタリア旅行。シラー(1759-1805)とドイツ文学古典主義確立 Kerr, John 1824-1907, 英 カー効果 Kerr effect – 物質の電気光学・磁気光学現象研究 Verdet, Marcel Emile 1824-1866, 仏 偏光理論 Moseley, Henry Gwyn-Jeffreys 1887-1915, 英 X線分光学基礎確立 電磁気学の応用Hertz HR 1857-1894, 独1888 電磁波の存在証明 Marconi G 1896 最初の無線通信に成功 (1901 大西洋横断無線通信成功) 電池 cella) 1次電池 primary cellLeclanché, Georges 1839-1882, 仏: 乾電池 dry cell (ルクランシェ電池) ⊖Zn|NH4Cl(ZnCl2)-H2O|MnO2, C⊕ (6.30) → 起電力1.5 V
⊖ Zn → Zn2+ + 2e-____________電子製造 電気エネルギーを化学物質変換貯蔵 = 充電 charging 1836 Daniell, John Frederic (1790-1845), 英 Ex. 湿電池 wet cell (ダニエル電池 Daniell cell) ⊖Zn|ZnSO4(aq)|CuSO4(aq)|Cu⊕ → 起電力1.1 V Ex. 鉛蓄電池 lead battery
__________________放電/2e- 充電 (battery) charge: 放電の逆反応 c) 燃料電池 fuel cell1800初頭 Davy H (英): 原理提唱 1839 Grove WR (英): 燃料電池による水の電気分解 1950代 Bacon FT (英): 水素-酸素燃料電池 Ex. アルカリ型燃料電池: 燃料として純水素のみ利用 (-)H2|KOH(aq)|O2(+)
放電機構 |
|
= 動力学 dynamics (s.s.) + 静力学 statics = 物理的性質(物理的特性) + 物理変化(物理的変化) 質点 mass point (or material point)の力学古典力学(Newton力学): 時間(実数)をパラメターに3次元ユークリッド空間に値を持つ質点運動を考察Def. 質量 mass (molarity): MKS → kg, CGS → g
慣性質量 inertial mass: 動かし難さから定義 Def. 質点系 system of point masses: 質点の集合 Def. 絶対空間 absolute space (Newton 1687): Newton力学の哲学的基礎
瞬間的に力が伝わる + 固定できる座標がある (現在不採用) 変化量(変化) variation速度 velocity, v: ベクトル (速さ speed, v: 速度の大きさ, スカラー)v ≡ v(t) = s'(t) = limΔt→0{v(t + Δt) – v(t)}/Δt = ds/dt 平均速度 average velocity, v = s/t (瞬間速度 instantaneous velocity)
(一般にv, etも時間と共に変化) [以降t省略]
= limΔt→0(1/Δt)·[(Δx)2 + (Δy)2 + (Δz)2]1/2 |
Ex. 円運動: 円周 circumferrence上の運動 → 中心を座標原点と一致 → r ≡ 回転半径 radius of gyration eφ: 角度方向への単位ベクトル
v(t) = dr(t)/dt·er(t) + r(t)·der(t)/dt O: 回転軸(回転の中心) pivot point
ω ≡ dφ/dt → v = rωeφ, v = rω Def. 加速度 acceleration, α ≡ dv/dt = d2r/dt2 [α = v' = r''] α > 0: 正の加速度 ↔ α < 0: 負の加速度 negative accelaration 平均加速度 average acceleration
A – B = C, A = B + C 向心加速度 centripetal acceleration,
α = –rω2er = –(v2/r)er
r(t + Δt) = (x + Δx, y + Δy, z + Δz) ∴ α = limΔt→0(Δv/Δt) = dv/dt → α = dv/dt → αx = d2x(t)/dt2 = x''(t), αy = y''(t), αz = z''(t)v (or α)各成分がx'(t)等(x''(t) …) → x, y, z座標が慣性系である必要 |
ニュートンの3大法則 (Newton's three laws of motion)第1法則 first law (慣性の法則 law of inertia)外力 external force (f)を加えなければ物体bodyは等速直線運動 uniform motion (linear motion) (含静止 at rest)を持続(向きの変化にも力が必要)⇒ 力: 質点sに及ぼされる(一般には時間に依存)= 3次元ベクトル 慣性系: 力を受けない物体が等速度で運動しているようにみえる(= 慣性力 inertial force (force of inertia))、固定したあるいは力の働かない座標系 Def. 慣性(座標)系 inertia (coordiante) system: 慣性の法則が成り立つ座標 Ex. 等速度 = 慣性系
↔ 非慣性 系noninertial system (noninertial frame of reference) → 重力9.8 m/s2に比べ十分小 経験的法則: 2つの質点が近くにあり、その間のみで作用及ぼし合う (Mach)→ 加速度は両質点を結ぶ直線に沿い互いに逆向きで、その大きさの比は質点運動状態によらず一定 Def. 慣性質量, m: 加速度 α1, α2 に反比例する量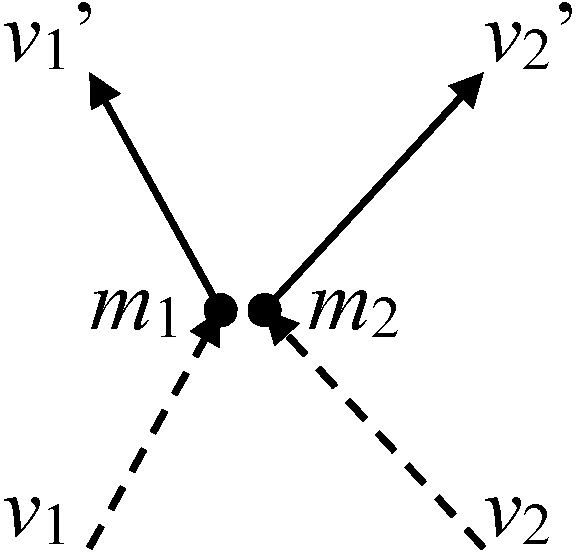
m1/m2 = α2/α1 → m1α1 + m2α2 = 0 → m1(v1 – v1') + m2(v2 – v2') = 0 ∴ m1Δv1 + m2Δv2 = 0
●m1m1' ●m2m2'
f1 = km1', f2 = km2': 第2法則 second law≡ Newtonの運動方程式 equation of motion: 運動量の時間的変化 = 外力⇒ 力 f は運動量 momentum p(= mv)の時間的変化に比例 f = dp/dt (仮定: 質量が時間と共に変わらない) = mα = m·dv/dt
m: 比例定数 (運動で慣性 inertia を表わす慣性質量) Ex. バネ秤で測定される物質の量 (物理量 physical quantity) Def. 重力質量 gravitational mass: 重力の影響を受ける強さを示す質量グラム重 gram-weight or gram-atomic weight (g重): 質量1 gの物体に作用する重力の大きさ Law. ニュートンの法則: 力、質量を(ほぼ)定義したもの基準物体により単位重量(1 kg)を定める Def. 単位 N (newton): 1 N ≡ fの力を加え1 m/sec/sec= 1 m/sec2の加速度を生じる 第3法則 third law (作用・反作用の法則 law of action and reaction)
● 作用 action と反作用 reaction は大きさが等しく向きは反対 = 同時に作用する力 concurrent forces: 作用点 point of action → 作用線 line of action f12 = –f21, fij: iがjに及ぼす力
(作用の力 action force ↔ 反作用の力 reaction force)
運動量の和 p1 + p2 = constant 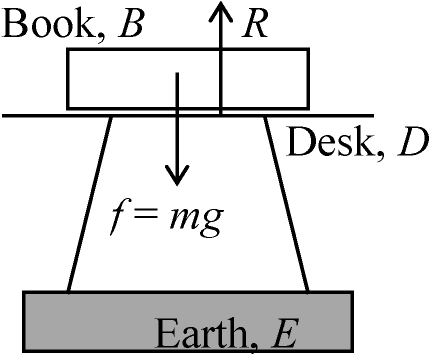
Ex. 磁力(磁気力) magnetic force: Def. 垂直抗力normal component of reaction, R
= 垂直力(法線力) normal component (of force) fの反作用 = -f (BがEを引く) ↔ Rの反作用 = -R (BがDを押上げる) (機械や道具に)加える力/作用させる力 effort (effort force) 一次元(直線上)運動 [非直線運動 nonlinear motion]1) 加速度-力-運動 f = constant [m : スカラー、速さによらず一定]
v(t) = dx(t)/dt, v(0) = constant, f = mα
(α = d2x(t)/dt2) |
= m{v(t) – v(0)}
∫0tfdt = m{x(t) – x(0)} – mv(0)t, ∫0t(∫0tfdt)dt = 1/2·ft2 m·dv(t)/dt = f = constant … (2) 微分方程式 ⇒ tで積分 → ∫m{dv(t)/dt}dt = mv(t) + v0' … (3) ∫fdt = ft + v0'' … (4) [v0', v0'': 積分定数、初期条件initial condition (IC)によって定まる] (3) = (4) ∴ mv(t) + v0' = ft + v0''∴ mv(t) = ft + v0'' - v0' ≡ ft + v0''' [v0'' - v0' = v0'''] IC: t = 0, v(0) = v0 → mv(0) = mv0 = v0''' ∴ v(t) = f/m·t + v0α = dv/dt = f/m [v(t) = f/m·t + v0)] x(t) = ∫v(t)dt + v0 = 1/2·(f/m)·t2 + v0t + x0 [xはICで定まる: x(0) = x0] a·d2x(t)/dt2 + b·dx(t)/dt + c = f(t) … (5) a, b, c: constant, f(t): 既知関数, x(t): 未知関数 → 求めたい関数 積分: 定数2個を含む関数 φ(t; a, b)が(5)を満足 → φ(t; a, b)は(最も)一般解
Ex. a = m, b = 0, c = -f, f(t) = 0 … (6), (7)式は(6)式のもとに(5)式の微分方程式を満足する Ex. 一定速度で走る自動車に加わる力: f = mα = 0, α = 0∴ f = 0 → 合力 resultant force = 0: 実際は空気抵抗(R)等の抵抗存在 Ex. 発進(停止)時に物体(自動車等)に加わる力: v(t) = αt, f = mαa) 落下運動 falling (action) →
自由落下free fallする物体質量(m)
重力, g → mα = mg, dx(t)/dt =dz(t)/dt = v(t)
重力加速度 gravity acceleration, acceleration of gravity) ≈ 9.8 m/s2 等加速度運動 uniform accelerated motion b) 抵抗力 resistance force ☛ 流体力学Def. 粘性抵抗(摩擦抵抗) viscosity or viscous resistance, βv
≡ 速度vに比例する抵抗(粘性から生じる摩擦力) ⇒ Law. ストークスの法則(ストークスの抵抗法則) Stokes law: βv = -6πηrv 速度vで運動する半径rの球状物体に対する気体・液体のβv 成立条件: Re (レイノルズ数) < 1-2 Def. 慣性抵抗(圧力抵抗) inertial (inertia) resistance, βv2
≡ 速度vの2乗に比例する抵抗  Ex. 無風の空気中を落下する雨滴:
Ex. 無風の空気中を落下する雨滴:
雨滴の受ける力 f = mg – R = mg - βv ∴ v(∞) = mg – βv = 0 ∴ v(∞) = mg/β // Def. 終端速度 terminal velocity: 等速落下運動をする時の速度, v(t) = mg/βEx. ρ: 水密度, r: 雨滴半径, βv: 粘性抵抗(= -6πηrv) → 質量 m = (4π/3)·ρr3 終端速度, v(t) = mg/β = {(4π/3)(ρr3)g}/(6πηr) = (2r2g)/9 → Th. 1. v(t) ∝ m→ Th. 2. v(t) ∝ r2 Def. 運動量, p ≡ mv → dp/dt = m·dv/dt = mα = f Def. 力積, J = f·Δt: 力fとその力の働いた微小時間Δtの積
= 運動量の変化 → 力が働けばJは必ず変化 角力積 angular impulse Eq. 力積-運動量の関係式 impulse-momentum theorem
→ f·Δt = mv1 – mv0 [運動量の変化は力積に等しい] = 1/2·mv2 – 1/2·mv02 |
|
E = EK + EP Law. 仕事の原理(仕事の法則) law of work Def. エネルギーenergy: 何らかの仕事をする能力 Def. (重力)位置エネルギー (ポテンシャルエネルギー potential energy) (s.l.) (gravitational) potential energy, Ep
→ Ep = mgz: xに無関係 Ex. 重力場、クーロン力、バネ力(力場ではない Ex. 摩擦力) Def. 仕事 work, W: 物体に外力 external force を加え物体を動かす時、外力が物体に「仕事」をしたという
= 外部からの仕事(外からされた仕事) external work 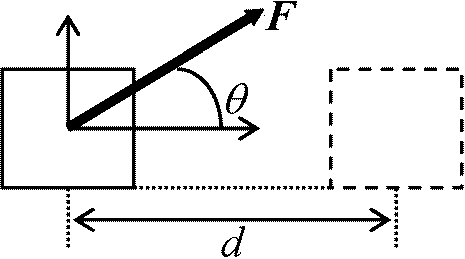
F: 物体を動かした力, 移動距離が0 → 力を加えても仕事は0 Def'. W = Fdcosθ (θ > π/2)Ex. 重量挙げ: 持ち上げた高さh
→ W = gmh → 位置エネルギー → P = W/t, 単位: 1 J/s = 1 W (ワット) A → Bに物体が運動エネルギーを(殆ど)持たない程度にゆっくり運ぶに要する仕事
WA→Bが途中の筋道に無関係な時、この力場は仕事エネルギーを持つ WA→C→B = WA→C + WC→B = WA→B = mgz Ex. 2 中心力場(万有引力 gravitation)Law. 逆2乗の法則 inverse-square law: 定量値発生源からの距離の2乗に反比例 → 光強度、万有引力、クーロン力 Ex. 3 バネの力 (= 中心場力): f = kxDef. 弾性エネルギー, EP
= 弾性力による位置エネルギー elastic potential energy, 保存力場における運動 → 力学的エネルギーは保存 Def. 運動エネルギーkinetic energy, EK
EK = 1/2mv2 (v2 = |v→2| = v→·v→ = v2cosθ = v2 (∵ θ = 0)) Law. (力学的)エネルギー保存の法則 law of conseveration of (mechanical) energy: エネルギー総量変化しない | ↑ Ex. 鉛直投げ上げ運動 → 鉛直上方への加速度-gの等加速度直線運動 t = t0, x0, v0 → t = t, x, v → v2 – v02 = 2α(x – x0) 保存力 ≡ Ep + Ek = constant → 1/2·mv2 + mgz = constant ↔ 非保存力 dissipative forces2次・3次元移動スティブヌス 1548-1620, 蘭: ベクトルvectorを力の問題に導入→ 運動方程式をベクトル式として理解 f = mα, m: スカラー 
A = (Ax, Ay, Az) 分力(力の成分) component force (component of force) 力の合成 composition of forces ↔ 力の分解 decomposition of force 
運動方程式: x, y, z座標系→ 静止または慣性座標系inertial frame of referenceが条件 立て方と解き方
初期条件v0 = (vx0, 0, vz0) → y方向考える必要なし |
y(t) = constant α = dω/dt = d2θ/dt2,
ω: 角速度. Ex. 3. 円錐振子 conical pendulum:
長さlの紐の一端に質量mの石結び他端を天井に固定
x-y軸: 石の回転する水平面
→ 座標軸は方程式が簡単になるよう設定 向心力 centripetal force
r = lsinθ … (2) (↔ 動滑車 moving pulley) Ex. 4. (定)滑車(プーリー) fixed pulley: m1, m2の運動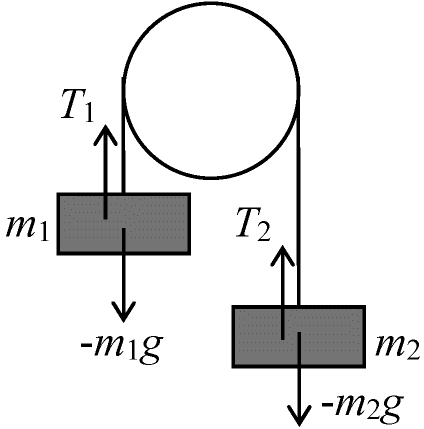
滑車の摩擦 friction = 0
zの原点はm1,
m1·d2z1(t)/dt2 = -m1g+T … (1) 力の釣合いと見かけの力 equilibrium of force and pseudo-force (fictittious force)一般に慣性系に対し加速度を持つ系に移ると"みかけの力Fα''が現れる ⇔ 真の力 net force → 3次元: oa = ob
⇔ 真の力 net force → 3次元: oa = ob
→ 力は釣り合っている 1) 遠心力(見かけの力) centrifugal force, fr or mαrfr = mαr = mrω2
r: 回転半径 (e.g., cm) 
T: 糸の張力, mg: 重力 a) 加速度系(非慣性系) = 回転台上から見る → 遠心力
等速円運動を行う振子pendulumは静止して見える
振子が等速円運動をしている → 駅を見ずAを見る → Aが動き出したと感ずる 3) ロープの切れたエレベータ中(重力が消失した感じ)
→ "重力"もみかけの力 (一般相対性理論), α0 = –g 4) コリオリ力 Corioli's force: 回転体の内周と外周の速度差から外側(内側)へ向かう運動物が回転体から見て"みかけ上"方向を変える力
= 進行の直角方向にでる見かけの力
→ f = 4π/T (コリオリパラメータ) → mfv |
|
Def. 周期運動 periodic motion: 一定の時間が経過するたびに同じ状態を繰り返す運動 Ex. 等速円運動 → 法線加速度 normal acceleration, 接線加速度 tangential accelerarion 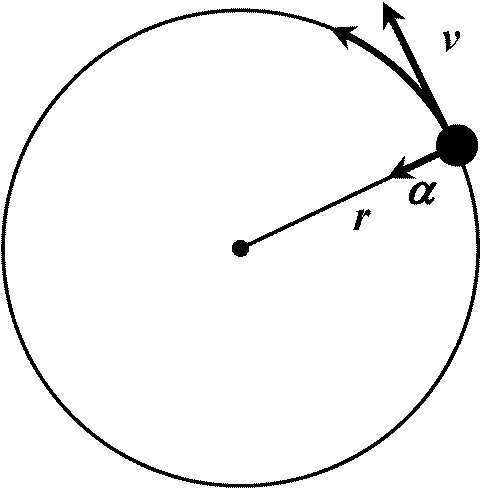
l (円周) = 2πr (ex. 秒, s-1)
→ fR = v/2πr Def. 向心力, F = mα = m·(v2/r) = m(2πfR)2r F = -m(2πfR)2r → F, m, α, v, fR, r間の関係式 → 殆どの場合を解くことが可能となるQ. 半径100 m (r)のカーブを72 km/h (v)で走る車 
→ 摩擦0となる路面の傾き(θ) A. v = 72 km/h = 20 m/s →
α = v2/r = 202/100 = 4 (m/s2),
Ncosθ = mg,
v2/r = gtanθ ∴ tanθ = v2/rg = 0.4, θ = 22° → fRT = 1, fR = 1/T Q.半径5 mのメリーゴーラウンドが周期10秒で回転
(1) 回転数(fR)
v = 2πrfR = 2π × 4 × 0.1 = 2.5 m/s Def. 単振動(調和振動, 往復運動) simple harmonic oscillation (motion): 釣合い位置からのずれ ∝ 復元力 → 振動 Def. 減衰振動: 外部から力を与えないと振幅が小さくなる振動 ↔ 強制振動 forced oscilation (vibration) Def. 波動 undulation: 振動が伝わっていく現象 Ex. 地震単振子(振子) simple pendulum
長さl、質量mの重り(分銅) weightの他端を天井につけ固定し振動させたもの Law. フックの法則 (Robert Hooke 1635-1703), f = -kx → 力が変位 displacement に比例 k: 弾性係数 elastic coefficient (バネならバネ定数 → 本質的な弾性率の1つ)
x: 変形量
(1) 球の向心加速度と、
球の向心加速度 a = r(2πfR)2 (m/s2), (r = l2)
(2) 球の向心力 f = mα = m·r(2πfR)2 |
単振動方程式 (調和方程式)
f = mα = –kx (k > 0: バネ定数), ω := √(k/m) → α = -ω2x
a = m, b = 0, c = +k, f(t) = 0 → x(t) = x0cos(ω0t + α) … (1')
(3)式を満足すれば(1')のx(t)は(1)式の微分方程式を満足する f = -kx = -mω02x → t =0, x(0) = 0, v(0) = v0 (-mω02 = k: バネ定数)
0 = x0cosα (α = π/2) → 一端に石を結び付けた紐の他端を固定し鉛直面内に回転させる 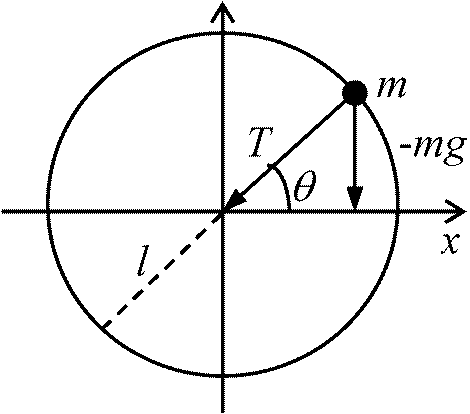
fx = mαx … (1), = –mlθ''(sin2θ + cos2θ) = –mlθ'' … (7)
(7)式はθ(t)についての微分方程式 → 解ければ運動方程式求まる δ(t) = Acos(ω0t + r), ω0 = √(g/l) (A, r, 初期条件で決定) クラドニ図形 Chladni's figures (独, 18世紀末, 音響学の父)水平に置いた板や膜 = 横振動 → 上に砂を撒く → 砂は節線(殆ど振動しない部分)に集まる → クラドニ図形 (ギター胴板の振動を調べる時等に使う) Ex. 等速円運動 uniform circular motion: l (原点の取り方にで異なる) = constant, |l| = constant = rp = mrv = mr2ω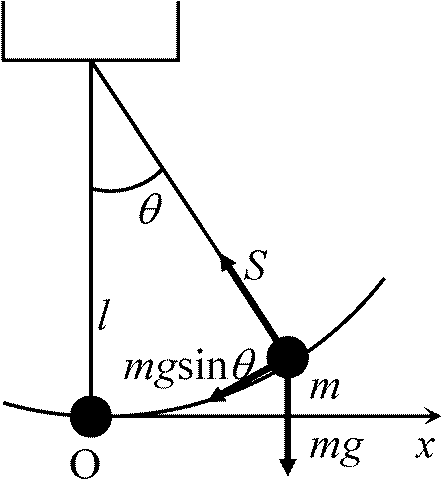
等速円運動 → 円の中心に向かって向心力が働く → これは中心力なのでlは一定
f = -mgsinθ ∴ α = (d2x/dt2) = -(g/l)·x
ω := √(g/l) → α = (d2x/dt2) = -ω2x → 単振子の周期Tはlのみで決まる → 振子の等時性 (1583年にガリレオがピサの大聖堂の時計を観察し発見, 逸話?) Q. 周期が1秒の振子の長さA. l = gT2/4π2 = (9.8 × 12)/(4 × π2) = 0.25 m g = (4π2l)/T2 → 重力加速度(g)を正確に求めることが可能 リップルタンク(水波投影機) ripple tank: 波動を観察するタンク |
|
= 機械工学 + 電子工学 機構と運動: 機構明確 → 効率良いシステム構築に有効 → Def. 機械: 構成各要素が限定された運動を行う
対偶 pair: 複数要素 element が互いに接触し限定された運動を行う組み合わせ 機械は、機構に着目すると構造を理解しやすい 理想機械 ideal machine → 不可能 運動の伝達と変換 transformation 節 node: 運動を与える側 = 原動節 driver →
節 node: 運動を与える側 = 原動節 driver →
[伝達・変換] → 受ける側 = 従動節 follower → 回転の平衡(回転のつりあい) rotational equilibrium 潤滑材 lubricant: 機械の磨耗を防ぐため用いる物質Def. 摩擦(力) friction ≡ F → 動かない間 f = -F
Ex. 机の上の物体を指で押す: fが小さい間は物体は動かない → F存在 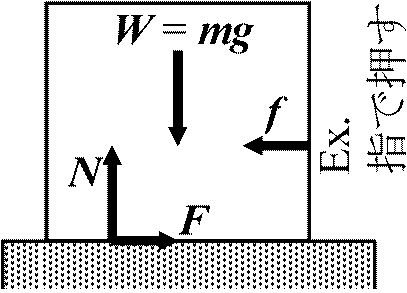 1) 静止摩擦 static friction: 静止している物体の摩擦力
1) 静止摩擦 static friction: 静止している物体の摩擦力Def. 最大摩擦力 Fmax: 物体が動きだす限界時点の摩擦力 Eq. Fmax = μN, N: 垂直抗力 → Def. 静止摩擦係数 coefficient of static friction ≡ μ s
接触する物体の材質、粗さ、乾湿等の状態で決まる定数
Ex. 斜面上の物体(0° ≤ θ ≤ 90°): N = Wcosθ, F = Wsinθ
静止の条件 F ≤ μN = μWcosθ ∴ tanθ = sinθ/cosθ ≤ μ 摩擦角 angle of friction: 傾斜を増し物体が滑り出す時の角度 2) 滑り摩擦(運動摩擦, 動摩擦) sliding friction: 接触する2つの物体間の速度差を減らす摩擦Eq. Fmax = μ'N → Def. (運)動摩擦係数 coefficient of sliding friction ≡ μ' [一般則] 0 < μ' < μ Ex. 斜面を物体が滑り出す: N = Wcosθ, F = μ'N = μ'Wcosθ, W = mg 物体に作用する力の斜面方向成分, F// = Wsinθ – F = mg(sinθ – μ'cosθ)
加速度, α = F///m = (sinθ – μ'cosθ)/g
前進させる力 = エンジンの働きで誘起された道路による前向きの摩擦力 Ex. 直線運動(直動) liner motion, 揺動 shaking, swing 3) 転がり摩擦 rolling friction
→ 回転中心 center of rotation と瞬間中心 instantanueous center: 円以外では異なる Ex. 回転rotation, revolution, 旋回gyration 1. 歯車(ギア) gear 伝動装置回転円盤側面に動力伝達のための凹凸を付けたもの Ex. モータa. 軸位置関係: 二軸が平行/二軸が直交/その他 b. 歯形状: 軸心に平行/弦巻状/その他 [標準平歯車の計算式] 歯車規格 → モジュール(歯の大きさ) m (mm), 歯数 Z, 歯幅 B (mm)等で表す 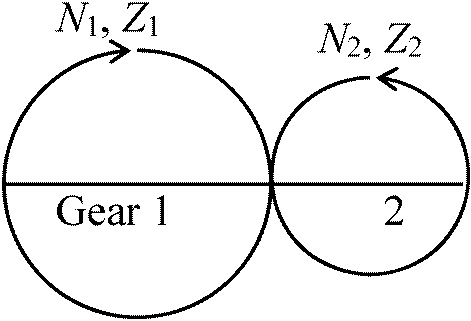
ピッチ円直径 diametral pitch, mm, Dp = m·Z = m(Z1 + Z2)/2 Def. 速度比speed ratio, i = N1/N2 = Z2/Z1
応用: Ex. ゼンマイ、ガソリンエンジン gasoline engine |
2. リンク機構 link mechanism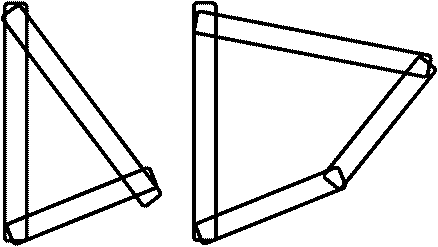 運動形態変換装置: 回転運動 → 他の運動に変換
運動形態変換装置: 回転運動 → 他の運動に変換3節以上の節を、主に回り対偶、滑り対偶により連結した組み合わせ
Ex. (三節リンク = 構造体), 四節リンク = 運動変換に利用, (多節リンク = 動き限定できない) Ex. クランクシャフト crankshaft
揺動節: レバ lever = 限定された範囲を揺動する節 3. カム機構 cam mechanism
円板カム plate cam: 回転円板の円周側面に従動節設けたもの Ex. エンジンのカムシャフト
立体カム solid cam: 回転球体表面や三次元形状による変位を利用し従動節駆動 軸受け(ベアリング) bearing: 回転軸を支えるよう作られた受け機構 てこ lever支点 fulcrum、作用点 load、力点 effortの位置を変化させ、力の大きさを変える器機
加える力の腕の長さ effort arm (effort distance) 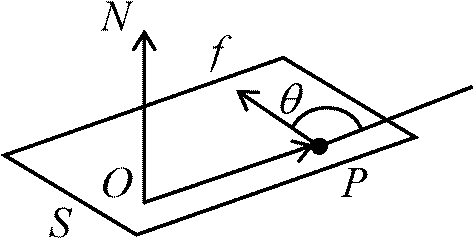
N:: ものを回すときの強さ(とイメージ) → 力の能率 r: 腕の長さ torque arm
N = rsinθ [中心力 central forceならばr = constant]
→ P1/P2 = l2/l1, or P1l1 = P2l2 2) 作用線が不一致: 2つ以上の平行な力が働くときの合力
MO = -P1l1 - P2l2 -P3l3 + Pxlx = 0 [釣り合う場合] → W = Σi=1nmig = mg := 0 → 重心が求まる 道具類クランプ(つかみ) clamp: 物(Ex. 梁と梁)を繋ぐため等に打つ金具。両端を直角に曲げたコの字型をするエンジン engine→ 吸入行程 intake stroke→ 爆発行程 power stroke → 排気行程 exhaust stroke:
圧縮過程 compression stroke
Ex. アクセル → 車加速 → 働く摩擦力 = 駆動力 |
質点系の運動量と角運動量Def. 剛体 rigid body: 力を加えても、変形しない物体(理想)
剛体として扱えるか否かは問題による vs 鉄球を叩くときに出る音 = 弾性体(変形し音が出る) 全体としてのエネルギー(重心の運動エネルギーと重心の周りの運動エネルギー)が無視できる位小さい
m1, F1__m2, F2
外力に応じ単体で存在し得ず、発生しても合力は0 ↔ 非弾性衝突 inelastic collision: 熱・変形 重心 center of gravity (質量重心 center of mass)重心質量は外力のみで決定→ 質量は全質量が重心に集まった様に振る舞う 重心の性質
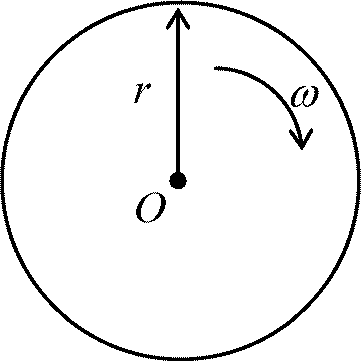 1) 回転運動: 剛体: 大きさを持つ → 質点と異なり各点で速度が異なる
1) 回転運動: 剛体: 大きさを持つ → 質点と異なり各点で速度が異なるEx. 円盤 → 剛体を多数の質点miの集合と考える → ri:mi点の半径 点miにおける運動エネルギー, EKi = 1/2·mivi2 = 1/2·mi(riω)2 → 円盤全体の運動エネルギー, EK = Σ1/2·mi(riω)2 = 1/2·ω2Σmiri2 := 1/2·ω2I Def. 慣性モーメント moment of inertia, I = Σmiri2 = mr2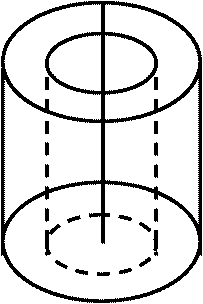 Ex. 円筒の中心軸の回りにおける慣性モーメント:
Ex. 円筒の中心軸の回りにおける慣性モーメント:
ρ = kg/m3, M = ρV = ρπl(b2 - a2) = 1/2·πlr(b2 + a2)(b2 – a2) = M/2·(b2 + a2) 慣性モーメントは中心軸を指定しておく必要 Th. 平行軸の定理質量 m, 剛体内の1点Oを通る回転軸(z軸)の周りの慣性モーメント I 重心Gを通りz軸に平行な軸の周りの慣性モーメント IG → I = IG + md2, d: Gとz間の距離
半径 R, 質量 M. 振子針金 → 長さ L, 質量 m (L > R)
接線方向の運動方程式 Ft = mαt 2) 歳差運動 precession: 回転軸が時間と共に変化する運動 → 外力による → dI/dt ≠ 0 Law. 角運動量保存の法則: 回転軸の周りの外力モーメントが0→ 物体固定軸の周りの角運動量は一定 Ex. 駒の首振運動, スケートのスピン, 水泳飛込み回転
回転の慣性 rotational inertia 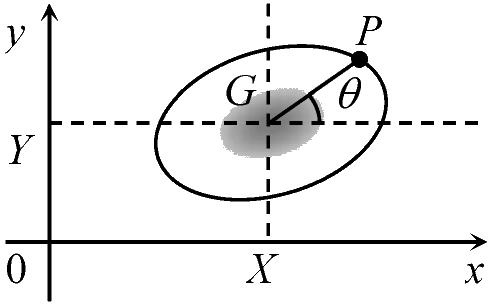 剛体の位置は、重心座標(X, Y)と重心の周りの回転角θが分かれば決まる
剛体の位置は、重心座標(X, Y)と重心の周りの回転角θが分かれば決まる運動方程式 mα = F (mαx = Fx, mαy = Fy)
α: 重心加速度,
IG: 剛体の重心を通りz軸に平行な直線の周りの慣性モーメント |
a) 滑り(並進 translation)運動: 質点の運動と同じく考えられる
r: 円柱(円筒・球・球殻)の半径 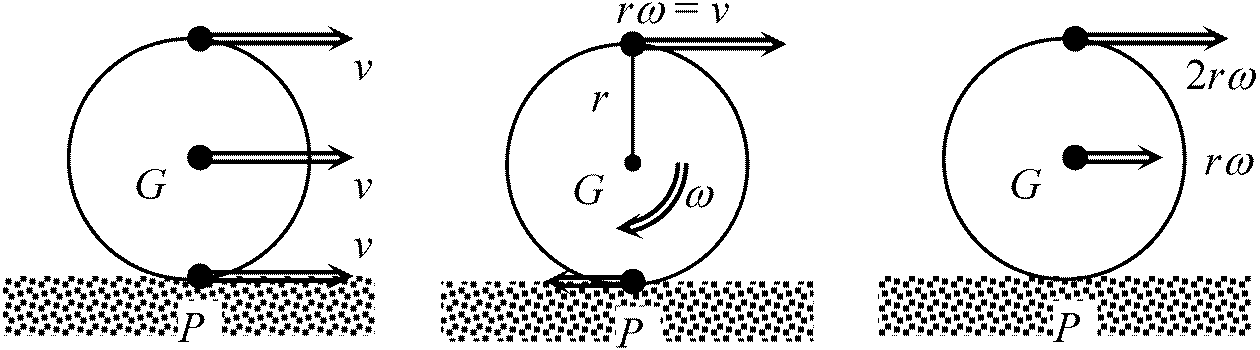 (a) 速度vの並進運動__(b) 角速度 ω = v/rの重心__(c) = (a) + (b) _____________________の周りの回転運動 _____________________-rω = -V b) 転がり運動
滑らない → 摩擦熱はない = 力学的エネルギー保存
-rω: 点Pにおける回転速度 これは質点の運動エネルギーmv2/2の[1 + (IG/mr2)]  Q. 斜面の転がり運動: ゆで卵はなぜ生卵より早く転がるか
Q. 斜面の転がり運動: ゆで卵はなぜ生卵より早く転がるかA. 位置エネルギー, mgh =
1/[1 + (IG/mr2)] + (IG/mr2)/[1 + (IG/mr2)] IG/mr2 大 → 遅く落ちる 2つの質点の運動(質点間に力が働くとき)Ex. 地球と太陽1) 2つの質点の衝突collision: 働く力 = 内力のみ 衝突前速度: v1, v2 → 衝突後速度: v1', v2' → 運動量 p1 = m1v1, p2 = m2v2, p'1 = m1v'1, p'2 = m2v'2
運動量保存則 p1 + p2 = p1' + p2'
v'1 = {(m1 – e·m2)v1 + m2(1 + e)v2}/(m1 + m2) μ = m1m2/(m1 + m2), or 1/μ = 1/m1 + 1/m2
Def. μ: 換算質量 reduced mass
2体の運動は1体の運動と重心の運動に分離出来る 2つの力によるモーメントは、それぞれの力の作用する点間を位置ベクトル r → N = r × F N: 偶力モーメント moment of a couple, F: 力(偶力), ×: 外積 剛体に働く任意の力は、1組の偶力と、剛体の重心を並進させる力に分解できる (剛体の力学的)運動エネルギー, EK
= Σ1/2·mivi2 = 1/2Σmi(ri⊥)ω2 = 1/2Σ(miri⊥)ω2 – 1/2·Iω2 I': 重心を回る軸の回りの慣性モーメント, ω': 重心の回りの角速度 一般に dL/dt = N … (1) → dL'/dt = N' … (1'), N·d2L/dt2 = F … (2)
|
|
無重力状態 null gravitional state (無重量状態 weightless state): 重力に逆らって働く力がない = 重力加速度で自由落下してる状態 微小重力 microgravity: 無重力に近似可能な状態 [近似可能な状態] Q. エレベータ: 下向き加速度 = 1 m/s2, 乗る人の体重 m = 50 kg→ 床から受ける垂直抗力Nを計算 A. 人に働く地球の重力, W = mg = 50 (kg) × 9.8 m/s2
= 490 kg·m/s2 = 490 N (= 50 kgf) ∴ N = mg – mα = m(g – α) = 50 (9.8 – 1) N = 440 N = 45 kgf → エレベータが降下している間、体重が5 kg軽くなったように感じる 万有引力 universal (constant of) gravitation →万有引力の法則 law of universal gravitation (universal law of gravitation) Law. ニュートンの万有引力の法則 Newton's law of universal gravitation
1) 2物体の質量Mとmの積のMmに比例 Def. G: 重力定数(万有引力定数) (uiversal) gravitational constant
= 6.67259 (≈ 6.67) × 10-11 Nm2/kg2 2個の球間に働く万有引力の大きさFは A. F = G·m·m/r2 = 6.67·12/0.052 = 2.7·10-8 NQ. rE = 6.37·106 m → 地球の質量を求める A. ME = grE2/G → 6.0·1024 kg 人工衛星: ニュートンが予測(プリンキピア中に見られる) 人工衛星の結合エネルギー binding energy of a satellite 一方的な中心力 Ex. 地球・人工衛星の軌道 orbit (trajectory)Def. 中心力: 固定点と作用する物体を結ぶ直線に沿って働く力
→ 固定点 = 力の中心 → mg: 重力 = 中心力
v: 人工衛星速度 → 運動方程式: mg = mv2/r ∴ v2 = rg → v = √{(6.37 × 106 m) × (9.8 m/s2)} = 7.9 × 103 m/s 軌道上の速度 orbital velocity: 人工衛星は7.9 km/s (= 周期84分)で動く |
地球と月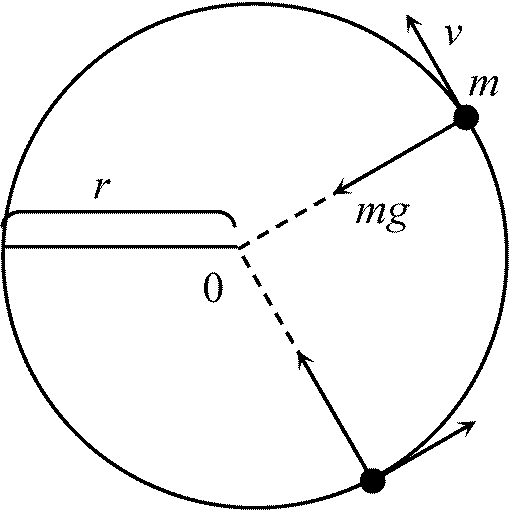 gM: 月が地球に向かい落下してくる加速度,
rM: 地球の中心と月の中心間の距離,
gM: 月が地球に向かい落下してくる加速度,
rM: 地球の中心と月の中心間の距離,RE: 地球の半径 → rM = 60·RE
→ gM/g = RE2/r2 = 2.7 × 10-3 m/s2 TM: 月の公転周期 (27.3日 = 2.36 × 106 s),vM: 月の速さ → vMTM = 2πrM αM: 地球の周りの円運動向心加速度
→ αM = vM2/rM = (2πrM/TM)2·(1/rM) = 60RE·(2π/TM)2 万有引力による位置エネルギー: 中心力 = 保存力
→ 位置エネルギー存在, E = EK + EP = constant W = ∫r∞G·(mM/r2)dr ≈ G·(Mm/r) 距離rの2物体間の万有引力による位置エネルギー, U(r) →
W = U(∞) – U(r) = -U(r)
物理的考察 ケプラーの惑星運動の法則 Kepler's laws of planetary motion地球の衛星(= 月)および人工衛星は一般に楕円軌道を回る
遠地点 apogee: 軌道上で地球から最も遠ざかった点(人工天体: 地表-遠地点までの高さを扱うこと多)
太陽の周りを回る天体(惑星、小惑星、彗星、人工惑星等)に対し: 近日点 perihelion ↔ 遠日点 aphelion → 多体問題 many body problem: 互いに相互作用する3体以上からなる系を扱う問題
2体問題: 厳密に解ける (Ex. 太陽-地球) → 月の運動も考える = 3体問題 |