(2022年4月19日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 電磁スペクトル
|
Def. 媒質 medium (pl. –a): 波動を伝える物質
Ex. 音において空気は媒質だが、真空は媒質ではない Def. 波動(波) wave: 媒質の一部に力学的変動→ 変動が隣接部に伝わり順次媒質中を伝播(伝搬) propagation 縦波 longtitudinal wave波動を伝える媒質自身の運動方向が波動の伝わる方向と一致した波媒質の圧縮・膨張の伝播 → 疎密波(圧縮波) compression(al) wave [(波の)疎 rarefaction] 気体・液体・固体全ての中を伝播する Ex. 音波 sound wave (acoustic wave, sound wave) [= 音 sound] 横波 transverse wave (transversal wave)それが垂直となる波固体の中を伝播するが横ずれに対する復元力がないので気体・液体中は伝播しない Ex. 電磁波, ぶら下げたバネの伸縮 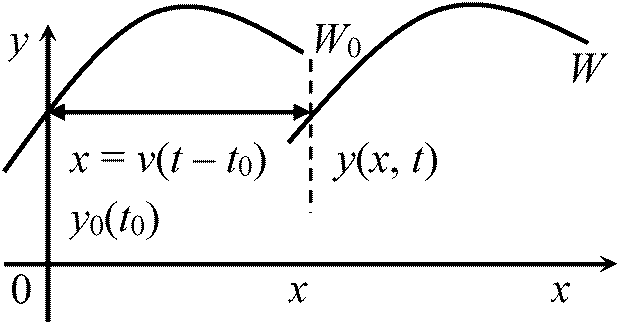
波動現象記述x方向に伝わる1次元的な波動の時間tにおける位置y0(t) = asin2πvt
y0: 原点0における媒質そのものの変位の大きさ(初期値)
→ y(x, t) = y0(t – x/υ) = asin2πv(t – x/υ)
角振動数(角周波数) angular frequency: 単位時間に回る角度, ω = 2πυ → 変位の大きさy(x, t)はωt – kxのみで決まる → (ωt – kx) + 2πn (n: ingteger)の時に変位の大きさは等しい ≡ 位相 phase逆位相の(位相がπずれた) in opposite phase ↔ 同位相の(位相が同じ) in phase 波動方程式 wave equation: 正弦波波動関数の拡張a) 弦stringを伝わる横波= 定常波(常在波) stationary wave (standing wave): 同じ所で振動続けるx軸に沿い張力Tで張った細い弦 → 直角方向に引き横波を発生させる 定常波の振動数fは不連続数 固有運動 proper motion固有振動 characteristic vibration: 物体が固定周波数と波形で振動する性質 = 外力周期と同周期で振動 → 固有振動数 character (or natural) frequency 共振(共鳴) resonance, sympathetic vibration: 振動体固有振動数に近い周波数入力 → 振動体振幅増
共振系: 固有振動を持つ振動系(共振を起こす性質がある系) – 固有振動は一般に1つでなく無数 |
 微小部分QQ'の運動方程式:
微小部分QQ'の運動方程式:固有周波数: 固有振動を生じる周波数
弦: 長さ、重さ(太さ)、張力により固有周波数決まる
共鳴吸収 resonance absorption b) 水面を広がる波= 進行波traveling wave (progressive wave)
(波の)山crest ↔ (波の)谷 trough ドップラー効果 Doppler effectDoppler 1803-1853: 音・光の波長、振動数変化音源: 速度uで運動, 振動数f0、波長λ0音波発生 → 静止観測者が受ける音波λと振動数 f (音速a0) λ = (a0 ± u)/f0 = λ0(1 ± u/a0) ドップラーシフト Doppler shift |
気体中にできる疎密派(縦波) = 音の波モデル wave model of sound
音波回折 accoustic diffraction波の強めあう線(点) line of reinforcementソナー sonar (sound navigation ranging): (超)音波使い船舶・魚群の距離・方位測定する水中音響探信機 ソノメーター sonometer: 音の高低の測定装置 音響学 accoustics「音」研究の総称 (物理学・心理学・社会学)建築音響学: 音伝播や音環境 + 騒音制御工学: 騒音・振動 + 音楽音響学: 楽器音響や音楽知覚・認知 「音」という言葉の意味: 空気振動としての音 ↔ 生じる感覚(日常生活使用多)
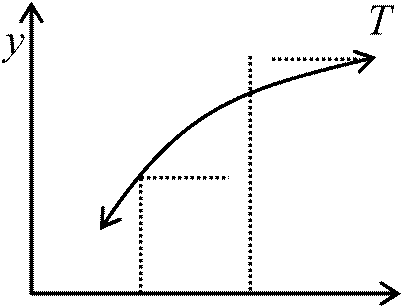
音を聞く意味 空気質量 = 1.2 kg/m2 → この振動が波動として空間伝わる → 空気が押される → 押された空気が密集し回りより(密な)高圧力部分生じる → これが隣の空気を押す(高圧力間に低圧力(粗)部分できる) → これを繰り返し波が伝わる 音速 velocity of sound (spped of sound) 空気中 = 340 m/s (温度高 → 音速大) (水中 = 1500 m/s) Def. マッハ数 Mach number: 流体の流れの速さと音速との比Ma = U/a (U: 流体速度, a: 音速) 音の伝播点音源と球面波spherical wave: 点音源発生音波 → 球面状に広がり(球面波)、距離に反比例し減衰(距離減衰)音源点でなくても音源十分小さい ≈ 点音源 非減衰波: 平面波は球面波のように広がらず減衰しないEx. 管の中を伝わる音波 反射と吸音: 物体に当たると一部は反射し残りは吸収(吸音)される屈折と回折: 原則は光同様直進 rectilinear propagation → 曲がる場合 (Cf. 電磁波) 可聴周波(数) audio frequency: 20-20000 Hz (20 kHz)程度の振動範囲個人差大 Ex. 年齢↑ → 上限周波数↓ 難聴: 騒音の影響等である範囲の周波数音が聞こえなくなる最小可聴値: 周波数により値異なる(低周波数音ほど最小可聴値小 – 感度低) 等ラウドネス曲線: 人間の耳に同じ大きさに聞こえる音の周波数と音圧レベルを示したもの Ex. 1000Hz 40dBの音と同じ大きさに聞こえる100Hzの音は約52dB位 音3要素 three elements of sounda) 音程 (tone) pitch音高低 = 周波数Ex. ド·レ·ミ … ド Ex. ドラムセット(バスドラム = 低音/シンバル = 高音) 周波数と音高の関係: 標準高度(楽器音域等), A = 440Hzメル尺度 1000 メル(mel) ≡ 1000Hz, 40dB音の高さ → 高さ2倍音 = 2000メル、半分 = 500メル
周波数高くなると、メル尺度値も大きくなる
→ 音階 musical scaleで1音から8度隔たる音(の隔たり) → 12平均律が多い 周波数バンド: 対象周波数範囲を一定の法則で区切った周波数帯
オクターブバンド: ある周波数を中心に上限下限周波数比が1オクターブとなる周波数帯域 b) 音色 tone高さと大きさが同じ2音が違って聞こえる、その違いEx. 同じ高さの音を違う楽器で、同じ大きさで演奏した時感じられる違いが音色差 純音: ある1周波数成分で構成される音 ↔複合音: 複数の異なる周波数成分から構成される音 日常音(楽器音、音楽、騒音、話声等)の殆ど 倍音 overtone: 振動数が基音振動数の整数倍である音弦楽器の弦を弾き振動 → 弦は固有振動開始 → 振動は全固有振動が同時に発生し重なり合った形になり全固有周波数に対応する音発生 基音(第1倍音): 固有周波数中で最低音 ⇔ 上音(第2, 3, … 倍音): 基音より高
基音 = 第1倍音: 他成分を周波数低い方から第2,第3 … 倍音と呼ぶ 白色雑音(ホワイトノイズ) white noise: 全周波数成分を含む音 c) 音量 loudness音の強さ sound intensity – 音の強さのレベル intensity level≠ 音の大きさ: 感覚的・主観的なもので必ずしも「強さ」と一致しない = 音圧(圧力変動幅): 物理的強さで客観的なもの可聴最小音量 threshold of hearing Def. 音圧: 「音がない時の空気中圧力 = 大気圧」からの音による圧力変化分Def. 音圧レベル (SPL): 「音圧」の対数(単位: デシベル)
1) 人間可聴音圧範囲 = 12桁にも渡る広範囲(対数表現) 室内音場反射音 → 屋外(自由空間); 反射 ≈ 0 ↔ 室内: 壁、床、天井から反射音 = 直接音 (音源 sound source (楽器等)から直接届く音) + 反射音
同音源 → 室内と屋外は同じに聞こえない(反射音の質と量異なる) 残響は室内音場の特徴 → 残響特性や質により聞こえ方が異なる Def. 残響時間(残響量): 室内音エネルギーが音源が鳴っている時の1/100万分に減衰するまでに要する時間セイビンSabine公式: 残響時間 = 0.16 × (室容積, m3)/(室の全吸音力) → 室容積大(大きな室) + 室内吸音材少 = 残響時間長 室の全吸音力: 室内にある音を吸収(吸音)する物質(吸音材)の量 残響特性: 残響時間は周波数により異 → 一般に低音ほど長く高音ほど短い
「室の全吸音力」は、吸音材性質に応じ周波数により異なるため残響時間も周波数毎に違う
1) 周波数毎の値を一覧表化
↔ 室内 = 反射音や残響のため距離減衰少 → 吸音材を適材適所に用い特性実現するよう設計 室内音響現象屋外では起こらない様々な現象 Ex. 残響特異現象(音響障害): ホールでは害になるものがあるので設計注意
|
音圧分布: ホール等では音圧のほぼ均一分布必要 → 音波動性により高音圧部分と低部分出来やすい
室内音響設計室内外騒音対策 – 室外騒音侵入防止(遮音材sound insulator)、室内騒音源(空調機等)対策音響障害(特異現象)防止 目的に応じ音響特性設定: 反射音到来条件 → 室形状・残響時間等 → 吸音計画(内装計画: 建築学) 電気音響設備 室内音場予測方法設計段階でホールの音響特性予測は所望の音響特性を実現するのに必要1. 理論計算 a) 幾何音響学的手法: 音波動性無視(= 直接音-反射音干渉・回折等の波動現象なし)し、光同様に直進と幾何学的反射のみで音伝搬を記述 = 近似的 → 低音域で誤差大きくなる傾向
i) 音線法: 音を「音線」で表わし、個々の音線が壁や天井等の反射面での反射軌跡を追跡 2. 模型実験: 模型制作適切 = 実物に近似した結果 → 予測精度優れる → 経費高(縮尺1/10-1/20模型多)
模型中で音発生 → 直接測定か収録分析 録音を1/10速度で再生し実物ホール音が聞け、設計図段階で完成後を予想したホール音聞ける 予測ターゲット: 通常、室内音場の物理的諸特性(残響時間、反射音特性、音圧分布等)を予測
心理的評価-物理的量関係 → 未解明
ホール設計法: 音響評価は、最終的には人間の聴感に基づく主観的評価 可聴化方法: ある受音点に到達する全反射音を理論計算し、このデータと音楽信号を「畳み込み」と呼ぶ計算処理すると、その受音点で聞こえる音を実際に聞ける 音環境設計 (目的に応じた音環境): 空調等の熱環境や換気等の空気環境問題同様、快適環境に欠かせない。快適環境には、まず騒音排除必要。室内音響特性(残響時間、音圧分布)も住宅居室や商店でも必要 [ 騒音ストレス ] 騒音 noise風車騒音低周波音: 遠くまで届く - 定格出力↑/基数↑ = 低周波音↑前庭器官で振動感知 → 環境性睡眠障害・風車病・高血圧・心筋梗塞 風車騒音 = 残留騒音 residual noise + 風力発電施設発生騒音
暗騒音: 評価すべき全騒音 - 自動車等の一過性騒音により大きく変化 1) 静穏な地域に設置されること多 → 騒音レベル低くても気になる 2) 振幅変調音(AM音): ブレード回転に伴い発生 - ヒトが慣れるのは難しい スウィッシュ音 swish: シュッシュッbr /> サンプ音 thump: ドンドン 3) 純音成分: 機種によって増速機や冷却装置から発生ウィーン、ブーン 騒音(雑音)排除騒音レベル noise level → 騒音計 sound level meterうなり beat: ピッチ(音の高さ、音高)が僅かに異なる2音
各々の基音周波数の差に相当する周期で音の強弱が聞かれる現象 Ex. 2室隣接: 発生騒音は壁を透過し侵入 → 壁遮音性能低 → 静穏室内環境減・プライバシー問題(集合住宅等で問題) → ホール-ホール-リハーサル室間遮音 + 屋外騒音が室内に侵せぬよう遮音 Def. 透過損失: 壁で音が減衰した量をdB表示したもの → 壁等の遮音性能壁に入るエネルギーの壁を透過するエネルギーに対するエネルギーの比 透過損失に関する質量則: 単層壁(一重壁) → 壁重量 ∝ 遮音性
壁重い + 周波数高 → 遮音性能(透過損失)↑
防御 → 機械振動を建物躯体に伝えない = 「防振」等処理 残響過多: 残響は音楽聴取では必要 ↔ 長残響は会話や講演を聴く場合に音声明瞭度損なう
非常放送等、重要情報伝達の妨げになる危険がある 吸音不足: 室内騒音レベルは、吸音力が少ないほど高 →
吸音力不足では残響過多 + 騒音レベル高 → 音環境劣化 Ex. 管楽器・弦楽器・打楽器 → 一定周波数音発生(共振系) 音発生 → 音: 空気振動すれば伝播 → 空気振動方法
原因: 細いため振動しても十分空気動かない(物体振動が音になる) = 大きさ(面積・断面積)必要 音楽の3要素 three elements of music3要素が関係し音楽となる
|
|
Def. 電磁場(電磁界) electromagnetic field: 電場 + 磁場 → 電磁場の性質を明らかにするのが電磁気学 場 field = スカラー場(等高線、等圧線、等温線で表現) + ベクトル場(力線) 電気力学 electrodynamics場の概念 → 電気・磁気現象を説明 → 電場・磁場の性質を取り扱う物理分野 |
応用: 電気工学、電子工学(エレクトロニクス) electronics → 全電気・電子機器は電磁気の法則に従い動作 記号: E ≡ エネルギー. λ ≡ 波長 (m, μm, nm).T ≡ 周期(繰り返し時間) (sec, s). NA ≡ アボガドロ数 |
|
静電気 static electrocity, electrostatic = 2つの静電荷 static charge 間の静電気力 electrostatic force →
点電荷 point charch (point source): 空間的広がり無視できる電荷分布 接触電位: 異なる金属を接触させた時に生じる金属間の電位差 → 白金に対する電位差で定義 Th. 電荷(電気量 quantity of electricity) (electric) chargeの4性質(電荷の法則 law of electric charge)
原子 → 外側の電子を放しやすい物 / 他から電子を受け取りやすい物 (静電)誘導帯電 charging by (electric) induction = 2種類の物質を擦り合すと物質表面を介し電子のやりとり 電子を放す = 正電気 → 電子を受け取る = 負電気 (誘導電荷 induced charge)
電荷間力大きさ = 18 c (Newton力学完成当時)、万有引力同様、電気力も距離の2乗に反比例と予想 静電気学基本法則 basic low of electrostatics= 静電気に関するクーロンの法則 Coulomb's law of electrostaticsTh. 1. 帯電electrificationした2物体に働く力, F → 物体間距離rの2乗に逆比例 → F = k'/r2, (k': 比例定数) Th. 2. 2つの点電荷q1, q2: 片方の電荷が2倍 → その間に働く力は2倍 → F = k''·q1q2 ( k'': 比例定数)
誘電定数 dielectric constant Law クーロンの法則クーロン力 Coulomb force (電気力 electric force), F ≡ k·(q1q2/r2)
力単位 = N. 距離単位 = m
c0: 真空vacuum中の光速度 A. F = 9 × 109 × N·m2/C2·(10-6 C)2/(5 × 10-2 m)2 = 3.6 N (斥力) = 0.37 kgf → 370 gの物体に働く重力と同じ → 電気力は重力の約1039倍の大きさ: 正負電荷がほぼ完全にバランス → 普段電磁気的力感じない 固体の形が変わらないのは正負の電荷が入り交じり堅く引っ張り合っているため 電気素量(素電荷) elementary (electric) charge, quantum of electricity ≡ 1陽子の電荷, e ≈ 1.60 × 10-19 C→ 電子の電荷: -e ≈ -1.60 × 10-19 C 重ね合せの原理(線形) principle of superposition: 複数電荷の作用 = 個々の電荷からの作用の和
→ 非線形 = 原理不成立 それぞれの電気力 F1, F2, F3 → F1 = F1→2 + F1→3 拡張: n電荷q1, q2, …, qn, F1, F2, …, Fn → F1 = Σi=1nF1→n ファラデーの場 field→ 他所にある電荷によって空間が緊張状態化 → 置いた電荷に力が及ぶ= 電荷は空間を緊張させる性質 → 緊張が伝わり離れた所に力が及ぶ → 「場」の理論 Def. 場 field≡ 特定量を対応させた空間Ex. 部屋: 温度の場・気流の場 → 点で温度、気流の速さ・向き決定 場の概念は、クーロンの法則より多くの電気現象を説明でき本質的(電磁波は、場の考え抜きに説明できない)Def. 電場(電界) electric field, EE: 電荷等により作られる電気の場(ベクトル場) → E = –E0e
Def. 電場強度(電場の大きさ), E0: 1クーロンの電荷を空間の1点においたときに受ける力の大きさ → 電荷 q (電子e = –q > 0)の有無に関わらず電荷Qは空間のあらゆる場所に歪(電場)形成 電荷↑ → 電場↑ / 電荷から離れる → 電場↓ f = qE → ある位置にもう1つの電荷qがあると、それに力fが作用する Def. 電場単位: 上式からC/m2 (= V/m)、下式からN/C (= V/m)が使われるEx. 電場の視覚化: 細糸を短く切り油中に浮かべる。帯電体charge bodyがあると、電場は糸両端に反対の電荷を誘導し、糸は電場方向に沿い互いに端と端を接し整列 (Cf. 磁石周辺に砂鉄を置き、縞模様を作る) 力線 line of forceベクトル場を図式的に見やすく表す → 力線を描ける = 場の理解と物理現象把握に大切力線はベクトル場内に仮想した曲線: 場のベクトルの関係は ベクトル大きさ = (力)線密度linear density → (力)線がより集まる所のベクトルはより大きい 電場強度 (電場の強さ) electric field intensity (or strength) ≡ 電気力線密度 ある点での電場強度 electric field intensity at a point ベクトル方向 = 力線に引いた接線の方向 力線の接線 = ベクトル向き: 場の1点を通る力線 = 1 → 力線交鎖しない(ベクトル0点 – 交わることあり)Def. 電気力線 electric line of force: 電場を表す力線(電場の向きの線 electric field lines)
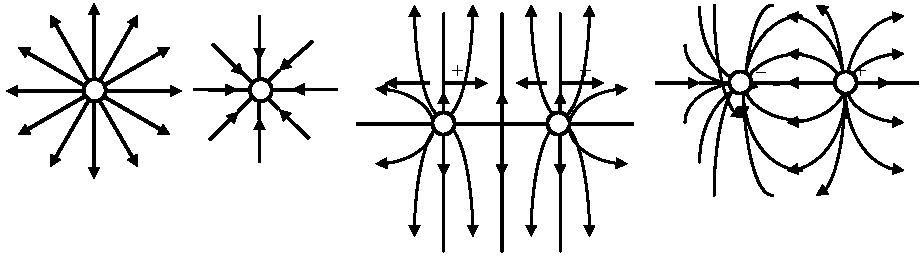 Ex. 1個の正電荷 1個の負電荷 同じ大きさの同符号の電荷 同じ大きさの反対符号の電荷(電気双極子) 電気双極子: 正負の電荷q, -qが極めて接近しているもの
d, 正負電荷間距離 → ガウスの法則 Gauss' law静電場基本法則の1つ: 場の考えに従いクーロンの法則書き換える→ 電場を使いクーロンの法則を表した関係: E = Q/(4πεr2)
E: 球表面での電場 Def. 電場強度: 球を貫き球の外へ出て行く電気力線本数
= 密度 × 面積 = 電場 × 面積 → E·4πr2 = Q/ε = (球の外へ出て行く電気力線本数) → 閉曲面全てで電荷は球の中心になくても成立: ∫E·ds = ∫ρdv
ds: 閉曲面微小部分面積 ≡ (電場の)ガウスの法則 Gauss' law 法則の示す物理的意味 →
(体積Sの表面から出ていく電場の和) = (S中の電荷の和)/(誘電率)
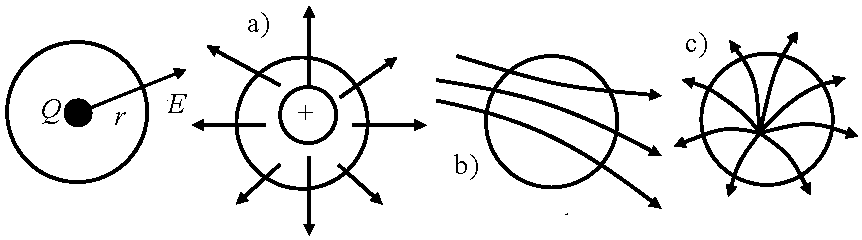 ガウスの法則(別説明) = 電気力線の始まりと終わりは必ず電荷
積分: 任意の閉曲面も微小平面は平面と近似可能 → Σ
ds, 電場に微小面積をかける
∴ ∫E·ds = Q/ε → 電荷からの距離概念無い ρ: 電荷密度(C/m3), dv: 面内微小体積 → ガウスの法則から、無限大の2枚の平行な平板に電荷が一様分布(下図)時にできる電場の大きさを求める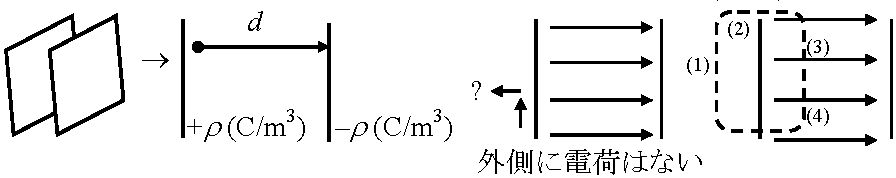
対称性: 板は無限に広いから電場は曲がらない。板外側の電場は終点がないので板外側には電場はない
左辺
→ 電場はどこでもρ/ε ≡ ポテンシャルエネルギー (静電ポテンシャルelectrostatic potential): 解放すると仕事をする → 正電荷を高電位の所で解放 → 低電位の方へ向かう運動 (Cf. 重力ポテンシャルエネルギー = 高さ) Def. クーロンポテンシャル(位置エネルギー), U(r) = k(q1q2)/r Def. 電位 electric potential, V: ある点で電位電荷あたり電気力による位置エネルギー → 電位差・電圧で計る量 V = (電気力) × (電気力に逆らって移動した距離)
電場どこでも同じ → 電場 E, 距離dl → V = -Edl
電場 = 電位の傾き → 電位の山の斜面の傾き →
電位の原点は、普通は大地の電位か、無限に遠い所の電位を原点(0電位)にとる V = UP/Q Q: 点電荷, UP: 位置エネルギー Def. 電位差 (electric) potential difference (電圧voltage), 2点間電位差potential difference btween two points2つの点電荷それぞれの電位 VP, VA → 電位差, VP – VA = (UP – UA)/Q = ∫Edl
Def. 単位: ボルト Volt, V (電池battery (cell)発明者ボルタの名) = J/C → 電圧計 voltmeter Def. 電子ボルト(エレクトロンボルト) electron volt, eV: 電極間電圧1 V時に電子の得るエネルギー 1 eV ≈ 1.602 × 10-19 J (1 keV = 103 eV, 1 MeV = 106 eV) Def. 電極 electrode: 電池・発電機等で電流が出入りする所。出る方が陽極、入る方が陰極
エミッタ(電子源) emitter: 電子顕微鏡やプラズマ発生器等の電子源 = 早い話が電極
→ 電気力線と等電位線は直角に交わる → 電場: 電荷(頂上)から離れるにつれ小
物質中電場(マクロな電場)これまで何もない空間を(暗黙)仮定 → 物質存在 → 電場はどうなる?物質内部は+/-電荷で満たされる 1電荷に着目すると、その電荷の回りに多くの他電荷がある 電気的性質に基づく物質区分物質の電気的性質を決めるのは、物質内部に自由に動ける電子の量
|
十分な強度の電界 → 強誘電体の両端面に現れる電荷 参考: 生体電気特性
誘電体に近い組織: 皮膚角質、脂肪、骨 ↔ 導体に近い組織: 筋肉、皮膚、内蔵、血液
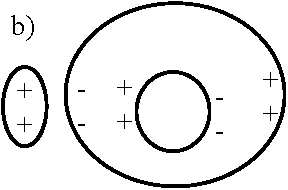
外部から導体に電荷を近づける(外部から電場をかける) → 導体中電子動き、電子が集る所は負、電子がない所は(原子核があり)正に帯電
→ 空洞中は外部影響全く受けない → 内部に電場できない = (b)不成立 空洞周り
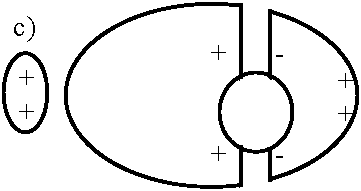
受ける力: 正電荷は右向きの力 ↔ 負電荷は左向きの力 → 空洞に切目あると電極はそれを越え動けず空洞中に電場形成(c) 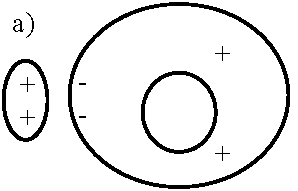
検電器 electroscope Ex. 箔検電器 leaf electrscope → 静電誘導利用 Def. 誘電分極(電気分極) dielectric (induced, charge) polarization: 誘電体分子中で電子は分子から出られないが、電場中では電子はその影響を受け居場所がやや偏る → 分子中で正電荷・負電荷を帯びた部分できる微視的 Ex. 水分子の様に正負の電荷が偏っている(分極している)分子がある 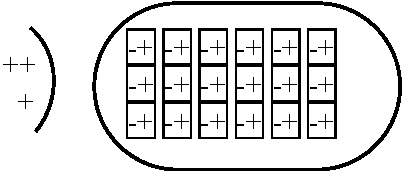 全体を眺めると、左にある正電荷が作る電場により分極の向きが揃う ⇒  ⇒ ⇒ 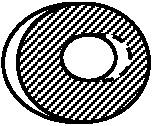 ⇒ ⇒負電荷は左に偏った分布になる 正電荷は右に偏った分布になる 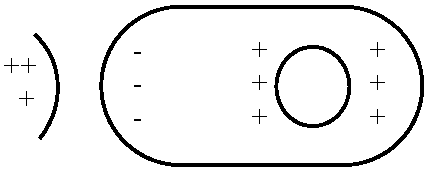 全体では、物質内部の電荷は打ち消しあい、端にだけ正負のバランスが崩れた領域が生じる その結果、誘電体内部では:

誘電体の外部では: 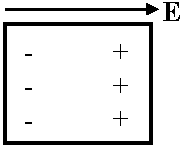 電気力は、静電かに始まり、負電荷で終わる
電気力は、静電かに始まり、負電荷で終わる→ 外部の電気力線は誘電体に引き寄せられる → 電気力線は誘電体をとおりたがる 誘電分極の大きさは物質によって違う → 誘電率 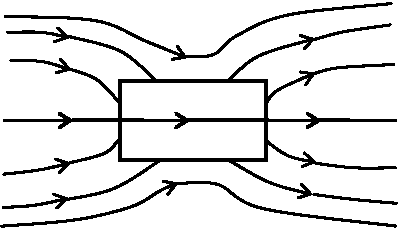
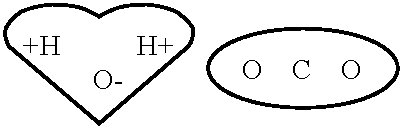 分極分子(eg, H2O)と非分極分子(eg, CO2)がある 分子構造違う → 誘電分極の大きさ異なる → 誘電分極の違いを比誘電率で表す Def. 比誘電率 dielectric constant, relative permitivity: 真空中を1 → 電気力線がどれだけ減るかの逆数 (物質固有値) E0 = εrE → (真空時の電場) = (比誘電率) × (物質中の電場), εr > 1 表. 物質の比誘電率(εr): 物質 = 比誘電率
空気 air (20°C, 1 atm) = 1.000536. 水 water ≈ 80
圧電効果 piezoelectric effect: 比誘電率が高い物質に強い電場を加えると電場の向きに伸縮する D = ε0εrE = εE
D (電束), ε0 (真空中の誘電率), εr (比誘電率), ε (誘電率) = ε0εr キャパシタ capacitor= コンデンサ (蓄電器) condenser平行板コンデンサ parallel-plate capacitaor: 導体板を向い合わせ、その間の空間に電場を閉じこめた電気素子 Def. 放電 (electric) discharge: 放電電流: 電位差 > 許容量 → 絶縁体が絶縁性失う → 電極間に流れる電流 → 絶縁体が気体(気体放電)の時を問題にすること多(放電機構は固体・液体では未詳な点多) Exp. 気体中に正負両電極を置く → その間の電圧を徐々に↑
→ 通常、気圧が低くない時
針先電極等、電場が局部的に高い部分での放電発光現象で、電極のギャップの局部に限られる
= 陽イオンの衝突による電極からの2次電子放出を必嬰としない レ-ザ―放電: 大出力パルス状レーザー光を気体中でレンズ集光→ レーザー光電場で電離作用 = 放電 → 絶縁破壊: 放電電流が流れること Ex. 純水、多くの樹脂(プラスチック)、油、セラミックCf. 電解コンデンサーelectrolitec capacitor Def. 静電容量(電気容量) capacitance (electrostatic capacity), C: 同電圧時に電荷を貯める能力の大小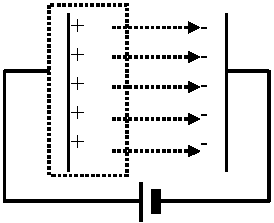 破線で囲まれた閉曲面でガウスの法則(∫E·ds = Q/ε)適用
破線で囲まれた閉曲面でガウスの法則(∫E·ds = Q/ε)適用
Q: 閉曲面内部の電荷 左辺 = ∫E·ds = ES
E: 極板間の電場の大きさ 電場-電圧関係: V = –∫E·dl (d, 極板間隔) → V = -∫0d(Q/εS)dl = Q/(εs)·d → 極板に蓄えられる電荷はQ = ε·(S/d)·V 反対側極板に符号が逆で大きさの等しい電荷を蓄える → 極板間の電圧と極板に蓄える電荷は比例(比例定数, C)Def. 静電容量(単に容量), C → 単位 ファラッドfarad, F = C/V μF (マイクロファラッド) = 10-6 F, pF (ピコファラッド) = 10-12 F ∴ Q = CV → (蓄えられる電荷) = (静電容量) × (かけた電圧)極板が平行平板 → C = ε·(S/d) = A/4πkd = ε0A/d
ε: 極板の誘電率 2) 面積が大きいと多くたまる(S: 大, C: 大) 3) 誘電率の大きい物質は電荷がたまるのを助ける(ε: 大, C: 大) 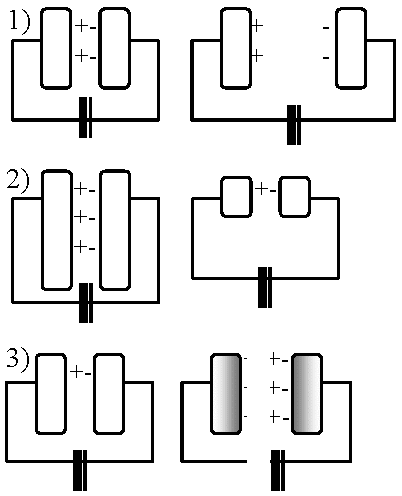 Q 1辺の長さが5 cmの正方形の2枚の金属板を1 mm隔てて向かい合わせた平行板キャパシタの電気容量
Q 1辺の長さが5 cmの正方形の2枚の金属板を1 mm隔てて向かい合わせた平行板キャパシタの電気容量A C = A/4πkd = {8.85 × 10-12 (F/m) × (0.05 m)2}/(10-3 m) = 2.2 × 10-11 F キャパシタの接続: 直列と並列並列接続 parallel connection (in parallel): キャパシタ静電容量 ∝ 面積 → 面積大きくなり容量も大きくなる
C = ε·S/d = ε·(S1 + S2)/d = ε·S1/d + ε·S2/d = C1 + C2
C = ε·S/d = ε·S/(d1 + d2) = 1/(d1/εS + d2/εS) = 1/(1/C1 + 1/C2) 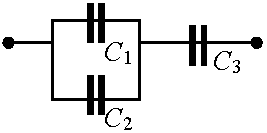 Q 図: 3つのキャパシタ C1 = 10 μF, C2 = 20 μF, C3 = 30 μF → 合成容量
Q 図: 3つのキャパシタ C1 = 10 μF, C2 = 20 μF, C3 = 30 μF → 合成容量A C12 [並列] = C1 + C2 = 10 + 20 = 30, C123 [直列] = 1/C12 + 1/C3 = 1/15 ∴ 合成容量は15 μF 電場エネルギー俗, 電気エネルギー electric energy電荷Qを蓄えるために必要なエネルギー → キャパシタの微小区間での蓄積を積分し解く 電荷dqを移動させるのに必要なエネルギー, dw = dE·dq E = V/d = q/(Cd) ∴ dw = q/C·dq 移動させた電荷の総和, w = ∫0Qq/Cdq = 1/2·Q2/C = 1/2·QV = 1/2·CV2[別解] 電場に着目 dE = dV/d = dq/dC = dq/εS ∴ dq = εSdE これを代入: dW = dEεSde ∴ w = ∫0ndEεSdE = εSd·E2/2 = 1/2·εSdE2 → キャパシタにはエネルギーが極板間の空間Sdに電場Eとして蓄えられる |
|
定常電流 = 電荷の流れ (厳密には磁場を生じさせるものは全て電流)
Ex 電解質溶液中の電荷の流れ 電流 current: アンペア ampere (A), I
1秒間にある面を通り抜ける電荷量 [+ → -]
電流計 ammeter (ミリアンペア計 milliammeter) 電線中を電流が流れるイメージ: 電子が走り抜けるのではなく、玉突き状に一番端が他端の1個を押し出す 検流計galvanometer: 小さな電流を測定できる電流計 ドリフト速度 v: 導線両端に電位差がない状態での電子の動き→ 平均106 m/sで正イオン間を乱雑に運動 → 抵抗に関連 Ex. 断面積 2 mm2銅導線に1A電流 → v = 3 × 10-5 m/s ≈ 1/100 cm/s 豆電球にスイッチswitch入れると直ぐ点灯 → フィラメント中に電場発生 フィラメント中の自由電子が電気力で動いた = 負極を出た電子によるものではない 電場は(ほぼ)光速度で豆電球まで伝わりフィラメント中自由電子を動かす エジソン効果 Edison effect: 電球の真空度計測に電球内に電極を入れた →電極に正電圧をかけるとフィラメント間を真空中だが電流が流れる効果 Def. 起電力 electromotive force (electron motive force), EMF, emf
= 電位差を一定に保ち続ける力 ds: 回路の微量要素s、E: 電場Eの回路方向の成分 半電池のEMF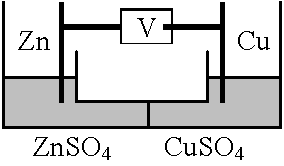
Zn|Zn++ (1 mol)|Cu++ (1 mol)|Cu
E0': 標準酸化還元電位(pH 7.0, 25°C, 1.0M)
E0'の大きさを比べればどちらが酸化型か還元型かが分かる
ΔE0' = E0'1 + E0'2 = RT/nF·ln([Oxi2][Red2]/[Oxi1][Red1]) = RT/nF·lnK ∴ ΔG0' = -nFΔE0' → F = 23062 cal
If ΔE0': pH 7.0, 25°C, 1.0 M → H2O ⇔ 1/2O2 + 2H+ +2e- 抵抗 resistance, R↔ 電気伝導 electrical conduction抵抗器(抵抗) resistors: 2点間に電位差V, 導線 高電位 → [電位移動] → 低電位 → 電流発生 電圧降下 voltage drop: 電気抵抗を持つ物質内部を電流Iが流れる →
流れる向きに電位が低くなる (= RI)
導電率(電気伝導度) (specific) electric conductivity, σ R, L (length), A (area), T = constant (温度一定) → R = ρ·(L/A) → ρ ≡ 電気抵抗率 (Ωm)
t0 → ρ0, t → ρ, ρ = ρ0(1 + a0(t – t0)) → a0 ≡ (電気抵抗率の)温度係数
t0 (°C) = 基準温度, ρt0 = t0での電気抵抗率
超伝導現象: 0 Kより高い温度で抵抗が0となる現象 Ex. 水銀
Ex. 極薄絶縁体(≈ 2 nm)層を挟み弱く結合した2つの超伝導体間 → 超電導電子対トンネル効果 → 絶縁層通し電流流れる
→ 直流ジョセフソン効果/交流ジョセフソン効果
直列: 距離長くなる → R = R1 + … + Rn R = (R1 … Rn)/(R1 + … Rn)
オームの法則 Ohm's law1827 Ohm GS: 電流 (I) ∝ 電圧(V), I ∝-1 抵抗 (R)Law ((I)小・(V)低時近似式): V = R × I → I = V/R, R = V/I 単位: (電気)抵抗 electric resistance → オーム ohm, Ω = [V]/[A] ミクロなオームの法則: 抵抗持つ物質に電圧かける → 物質内に電場生じ電子は加速される
↔ 物質中の多くの原子核と電子はやがて衝突し減速されエネルギー失う 比電荷 specific charge (of electron): 荷電粒子の電荷eと質量mの比
= e/m 加速電圧 acceleration voltage: 一定エネルギー(電圧)で加速(電圧)された同質量電荷比のイオンは、一様磁場中通過時、方向に多少開きがあっても同一点に収束できる = 方向収束 direction focusing 微小領域のオームの法則V = RI, R = l/(σS) → I/S = σ·V/l → V/lは電位の傾きを表す = 電場そのもの
R = ρ·(l/S) = l/(σS): 単位面積当たりの電流 ≡ 電流密度 R = ρ·(l1 + l2)/S = ρ·l1/S + ρ·l2/S = R1 + R2 回路 (circuit)電流の流れる通り路素子 element電気(機械)回路中で、自身の機能が全体の機能に本質的に重要な意味を持つ個々の構成要素
→ テスタ(回路計) circuit tester
Ex. 電源、キャパシタ、コイル、ダイオード、トランジスタ、ブレーカ(電流遮断器) circuit breaker等 円電流 circular current: 軌跡が円描く電流 Ex. コイル(円形導線) 電子素子 electron device: 半導体等の材料中での電子の振る舞いを利用した素子電子的情報の記憶情報処理等だけでなく、ダイオードやレーザー等のように電気を光信号に換える素子や、液晶等のように画像を表示する素子、微小な加速度や温度変化を検知するものなど、様々な機能 負荷 load: 電気エネルギー → 光、熱、音、化学エネルギー、仕事等に変換負荷容量: 回路等にかかる最大電気量(限界値) |
回路図記号電子回路書き表すために使う図: 部品 = 特定記号 → 配線 = 線で繋ぐこと実体配線図: 部品の絵を直接書いた図 → 面倒 + 部品増えると煩雑 + 個人差 → 回路図 直流電圧源 電圧は傍に書く。2個の長方形の細長い方が+(高電位方) (図中+-記号は実際不要)。電池記号だと記号1個で1.5[V]という使い方があるが、一般には1個で任意の電圧に使う 交流電圧源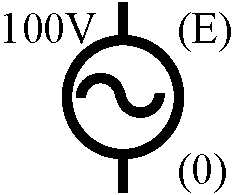
直流含め、任意の電圧源(s.s.)(直流は時間で一定という特殊なもの)。記号対称なため、一般に下側端子を基準に上端子が変化すると考える(図中0, E記号は実際不要。この記号は横向きに書くこと稀) 固定抵抗近年規格は細長方形記号だが、ジグザグ記号(端子線に対称にそれぞれ3山)も通用する。可変抵抗、半固定抵抗抵抗値が変わるもある コンデンサ condensor (キャパシタ)電解コンデンサでその間に電解液が入るものは斜線入記号、そうでなければ斜線なし記号使用。電解系コンデンサelectolysis condensorは一般に極性があり、+-を明記(逆接すると破裂したりし危険) グランド(基準電位)電圧基準点を示す。この記号がつながる線が「この点の電圧は」と言う基準電位となる。T字に斜線記号を使うが▽に電位0記号が多くなる 配線接続回路図では部品と部品は原則として縦横の線でつなぐ。ただ線が交差した場合には非接続、そこに黒丸がつく場合は接続を意味する。T字の場所は接続と断定できるが、省略せず黒丸をつける 配線非接続黒丸がない線の交差は自動的に非接続。線が飛び越えた書き方(右)もあるが必要ない 論理回路 (logic circui)・特殊回路
(s.s.) 回転角・移動量を電圧変換する機器・素子(s.s.)→
真空ガラス管中に2以上の電極を封入。整流・検波・増幅・発振等の働き。ラジオ・テレビ等に利用 直列回路 series circuit ↔ 並列回路 parallel circuit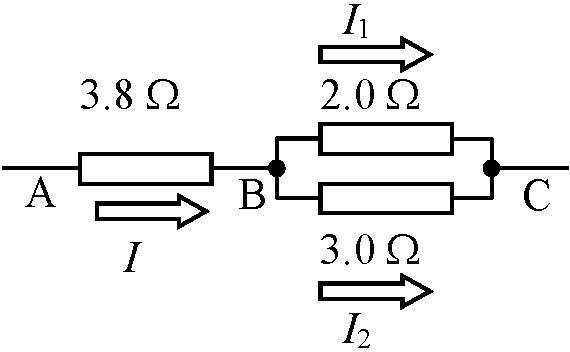 Q. 端子A, Cを10 Vの電源に接続
Q. 端子A, Cを10 Vの電源に接続
→ 危険: 回路抵抗小 = 高電流 → 導線や電源が発熱 (火傷等) ヒューズ fuse: 使用中機器に過電流又は短絡電流発生 → ヒューズ可溶体が溶断又は遮断し機器保護最も簡単で安価 = 広く利用 遅延回路 delay circuit: 入力電気信号を一定時間遅らせ出力する回路Ex. エコーのつくカラオケ装置 カーチョフ(キルヒホッフ)の法則 Kirchhoff's laws複雑な回路の電流を求めるときに良く利用される
閉回路 closed circuit : f → a → b → c → d → e → f (Va – Vf) + (Vb – Va) +(Vc – Vb) + (Vd – Vc) +(Vf – Vd) = 0 ↔ 開回路 open circuit→ カーチョフの第2法則 second law: 閉回路 → ΣV = 0 Def. 電位上昇 = 正(+), 電位降下 = 負(-) Ex. V1 – R1I1 + R2I2 – V2 = 0 → V1 – V2 = R1I1 – R2I2
第2法則 fabef: V1 = (R1I1 + R3I3), dcbed: V2 = R2I2 + R3I3 V1 = (R1 + R3)I1 + R3I2, V2 = R3I1 + (R2 + R3)I2
これを解きI1, I2を求める 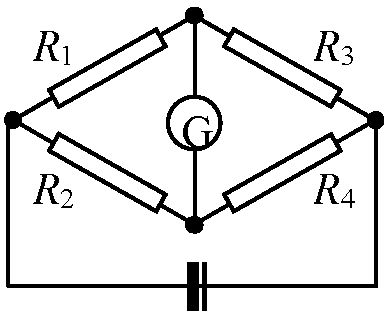
G: 検流計 → 値0となるときがブリッジの平衡 equilibrium ↔ 伝導電流: 電子が担う 電力 electric power, electricity≡ (電源・電流の)仕事率 = 単位時間あたりになす仕事の大きさ直流 direct current, DCEx. 電池: 正電荷Qを負極から電位がVボルト高い正極に移動させる時に電源がする仕事 = VQ
時間Δtに回路にIアンペアの電流が流れる → [単位] ワット(Wattに因む), W = J/s = V·A 電力量≡ 電流のする仕事 [通常単位] kWh (1キロワット時 = 1000 Wh) = 1 kWの電力が1時間にする仕事
Ex. 家庭用40W電球の抵抗
→ 電球の抵抗R, = V/I = 100V/0.4A = 250Ω Def. 消費電力量: 消費電力 × 時間 Ex. 消費電力が1kWの電気器具を一時間使用 → 1 kWh = 1000 W·3600 sec = 3.6 × 106 J 静電場の応用コピー機: 静電気を紙に与え帯電部分にトナーが吸着(ゼログラフィー xerography)X線発生器: 陰極からの放出電子は極板間にかけられた大電圧が作る電場の力を受け加速される。陽極衝突時に、その運動エネルギーは殆ど熱に変わるが一部はX線(X rays, roentogen rays)として放出 心電計 electrocardiogram
神経細胞: 外側正、内側負に帯電 → 興奮時: 電位が逆転し、それが周辺の神経細胞に伝わる |
|
= 磁界 (工学) 1820 Oersted, Hans Christian (1777-1851), デンマーク 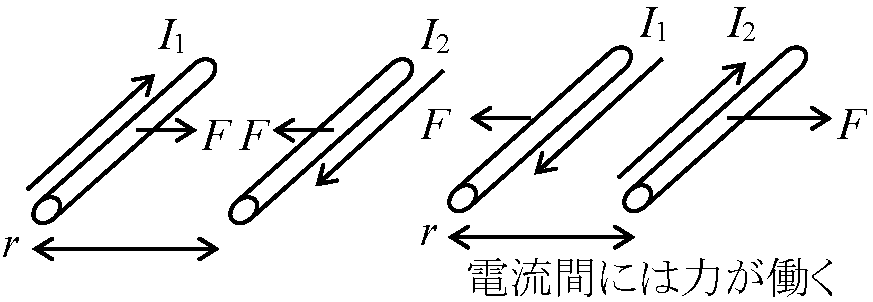
電磁気学先駆者 (磁場強度単位Oeは彼の名) 磁気誘導 magnetic induction: 導線の傍に磁石magnetをおき電流を流す → 磁石が導線と直角方向を向く→ 誘導磁荷 induced magnetism = 電流の磁気作用発見 磁気に関するクーロンの法則 Coulomb's law of magnetism電流間に働く力 → それぞれの電流の強さの積に比例+ その間の距離に反比例 F: 直線電流 linear currentのl mあたりに作用する力の大きさ → F = k·(I1I2/r), k: constant Def. 1 A(アンペア) ≡ 等しい強さの2本の直線状平行電流を1 m離したとき、それらの直線電流の1 mあたりに作用する力の大きさが2 × 107 N/mの時の電流の強さDef. 磁場 magnetic field, H磁気等により作られる磁気の場(電流の周りに生じ他の電流に力を及ぼす場)H = I1B, B = k·I2/r → 電流I1はその周りの空間に磁場Bを作る → 電流I2を持ってくると、それに力が働く → Def. 磁束密度(磁場) magnetic flux density, B
磁束flux (magnetic flux) → 磁束線 magnetic flux lines (line of flux) [磁場の向きの線 magnetic field lines] Ex. 磁気治療器 80 mT = 0.08 T (1000 mT = 1 T) 磁束計 flux meter: 磁束密度測定装置 → 磁化の測定にも利用 磁場が電荷に及ぼす力 = 磁場が電流に力を及ぼす場 → 動く電荷に力が及ぶ
電流を電荷の動きで表す: 導線に単位長さあたりqの電荷があり速さvで流れる → 電流, I = qv
→ 電荷は電場と磁場の両方から力を受ける → f = qE + qv × B 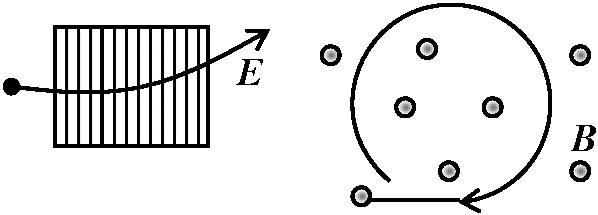 電荷の運動: 電荷が電磁場中で運動
電荷の運動: 電荷が電磁場中で運動
→ 電場・磁場から力を受け運動方向変わる Rule. 右ネジの規則 right-handed screw rule磁場の向き → 電流の流れる向きに進む右ネジの回る向き 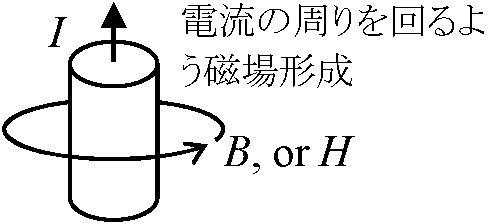 Law (静磁場基本法則): アンペールの法則(ビオ-サバールの法則)
Law (静磁場基本法則): アンペールの法則(ビオ-サバールの法則)
電流に働く力から、電流と磁場の関係を明らかにする
→ B = k''·I/2πr ∴ 2πB = k''I
一つの閉じた経路を考える
c: 積分経路が閉じている
∫cH·dl = I [HとBを使い分ける時: H ≡ 磁場, B ≡ 磁束密度] 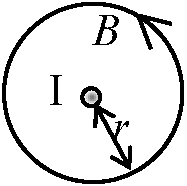 Ex. 1: 電流からの距離rの円を経路にする (Ex. 2ではr = 2r)
Ex. 1: 電流からの距離rの円を経路にする (Ex. 2ではr = 2r)
円周上ではどこでも磁場Bは一定。向きは接線方向 → ∃B·dl = Bdl ∴ ∫cB·dl = 2πrB = μI Ex. 2: 電流からの距離2rの円を経路にする
距離2倍 → 磁場の大きさ = 1/2 ∴ B' = B/2 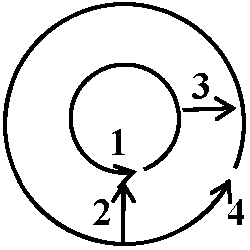 Ex. 3: 経路が電流を囲んでいない時
Ex. 3: 経路が電流を囲んでいない時
経路2, 4は磁場の接線成分がないのでB·dl = 0 磁場のガウスの法則↔ 電場のガウスの法則: 電気力線の始点・終点は必ず電荷「磁力線 magnetic lines of force (line of magnetic force) に始まりと終わりはなく必ず閉ループ(閉曲線)になる」 電場との相違点: 電荷相当の磁荷 magnetic charge は存在しない
磁荷の存在は理論的に許される(磁気量 magnetic charge)が未確認 磁気単極子(モノポール) magnetic monopole: 単一の磁荷のみを持つもの (未発見) 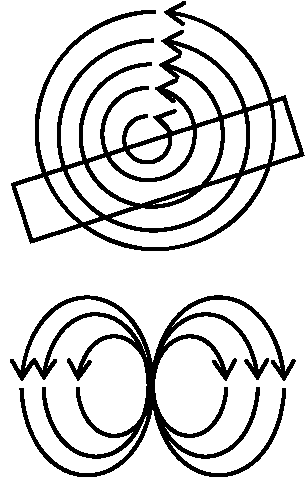 → ガウスの法則の右辺は常に0
→ ガウスの法則の右辺は常に0磁場のガウスの法則 Gauss' law: ∫B·ds = 0, ds: 閉曲面の微小部分面積 物理学的意味: (体積Sの表面から出る磁場の和) = 0 → 磁場を足しあわせる = 磁力線数: (S表面から外へでる磁力線本数) = 0 → あらゆる閉曲面で入った磁力線は必ず出る ≡ 磁力線に始点・終点なく必ず閉じる閉曲面の選び方によらず入る磁力線と出る磁力線の数は等しい 永久磁石も内部で磁力線はつながる 磁気現象: (アンペールの法則 + 磁場のガウス)の法則で説明可働く力はローレンツ力で説明可 物質中の磁場簡単な原子モデルでは、原子核の周りを電子が回る電子が作る小電流ループは非常に小さい磁石と見なせる(分子磁石)。物質磁性(磁気) magnetismは巨視的 大きさで分子磁石がどの程度見えるか(分子磁石が同じ向きをむき揃うか、好き勝手な向きをむくか)で決まる 電磁石 electromagnet コイル coil 鉄心に導線を巻いたもの(円状(円形)コイル circular coil)
コイル coil 鉄心に導線を巻いたもの(円状(円形)コイル circular coil)電流により磁石の向きが変わる → 電磁石に鉄心coreを入れると力が強くなる: 鉄心を入れると電流は増えてないのに磁束が増える → 鉄心中: コイルの作る磁場によって分子磁石の向きが揃う
永久磁石内部では分子磁石の向きが揃っている → 誘導磁化 induced magnetization (magnetization by induction) 物質により磁場が変化することを表す方法 →∫cB·dl = μI = μ0(I + Im) = μ0μrI = μ0(1 + χ)I Def. μ: 透磁率(magnetic) permeability
μ0: 真空中透磁率 電場における誘電率と異なる点1) 比透磁率は1より大とは限らない
常磁性体・反磁性体は必要のない限りμr = 1として扱えばよい
Ex. 鉄をずっと磁石につけておくと磁石になる Ex. 棒磁石bar magnet 強磁性体 = 磁気モーメントが全て平行に並ぶ小領域の集合 → その領域 ≡ 磁区 (magnetic) domain 直流モータ (electric) motor: 内部は磁場を発生させる永久磁石と回転するコイルで構成されるコイルに電流を流すと永久磁石の作る磁場から力を受ける。力はコイルを回転させる向きになり回転を始める スピーカ (loud) speaker: コイルに電流を流すと永久磁石による磁場から力を受けて振動板が振動サイクロトロン cyclotron: 荷電粒子加速器の1種 – 磁場中に荷電粒子を入れると円運動開始 円運動と同じ周期でディー Dee (dees)と呼ばれる電極で電場をかけると荷電粒子は力を受け加速する 磁気瓶 magnetic bottle電磁誘導 electromagnetic induction エルステッドやアンペールの研究 – 電流がその回りに磁場を作る
エルステッドやアンペールの研究 – 電流がその回りに磁場を作るFaraday: 逆に、磁場が電流を生じさせることも可能と考え、試行錯誤の結果、図の装置を作る
Faraday実験装置: コイルAスイッチ入切時にコイルBに電圧発生
→ 電圧の向きは変化を妨げる向きに生じる [レンツの法則Lenz's law] → V = –∂Φ/∂t, V: コイルに生じる電圧(V) –∂Φ/∂t: コイルを貫く磁束の時間変化率 Φ: コイルを貫く磁束(ウェーバ, Wb)、t: 時間 (sec) Def. ウェーバ weber, Wb (磁束単位)1 Wb/s磁束変化 → 1 V起電力発生[kg/m2/s2/A] 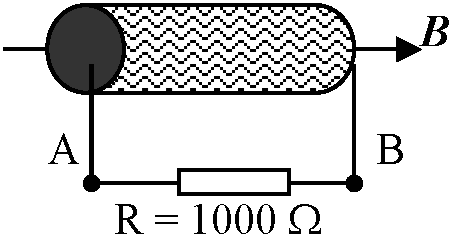 Ex. 数1000に巻いたコイル中の磁束が1秒間に10-3 Wbの割合で増加
Ex. 数1000に巻いたコイル中の磁束が1秒間に10-3 Wbの割合で増加
抵抗に流れる電流の大きさ, V = N·ΔΦ/Δt = 1000·10-3 = 1.0 (V) = RI |
→ Def. ファラデーの(電磁誘導の)法則 Faraday's law: ファラデーの法則を電場と磁場を使い表現
(左辺) = V = ∫E·dl, 磁束 Φ = ∫B·ds → (右辺) = –∂Φ/∂t = –∫∂B/∂t·ds
∴ ∫E·dl = –∫∂B/∂t·ds → (経路に沿う電場接線成分の和) = (経路を貫く磁束の時間変化) ファラデーの電磁誘導の法則 = 経験的発見 → 現在: 理論的証明済 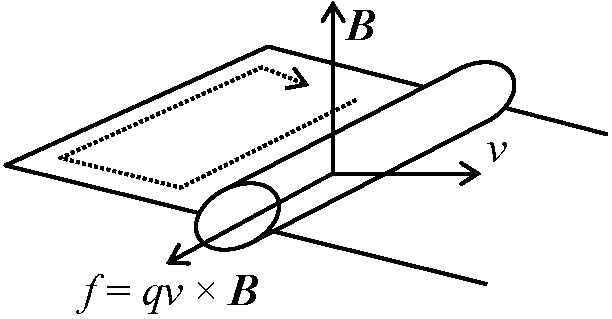 Ex. 導体でできた棒が均一な磁場中を動く(右へ進むと仮定)。棒はコの字の形をした導体と接しながら運動し、棒とコの字の導体で1つのループを形成し、自由に電流が流れるものとする
Ex. 導体でできた棒が均一な磁場中を動く(右へ進むと仮定)。棒はコの字の形をした導体と接しながら運動し、棒とコの字の導体で1つのループを形成し、自由に電流が流れるものとする
磁束密度Bの空間を動態の棒が速度vで動いている
導体棒中の電荷は磁場中を運動 電磁流体発電 (MHD発電) MHD (Magne-to-HydroDynamic) power: ファラデーの電磁誘導の法則を用いて行う発電 渦電流 eddy current≡ 金属塊中を電磁誘導によって流れる電流電磁誘導はループ上に作られた導体だけでなく、導体の塊でも生じる Ex. 強い静磁場(Ex. MRI装置)中で、金属板を立て手を離すと金属はゆっくり倒れる → 板を貫く磁束が倒れていくと共に減少し、減少させまいと電磁誘導が起こるため
ソレノイド solenoid: 絶縁した導線を密に円筒状に巻いたもの インダクタンス inductance (電気工学)電磁誘導の起こりやすさ → 静電場キャパシタンスと比較相互誘導 (相互インダクタンス) mutual inductance → 電磁相互作用 electromagnetic interaction 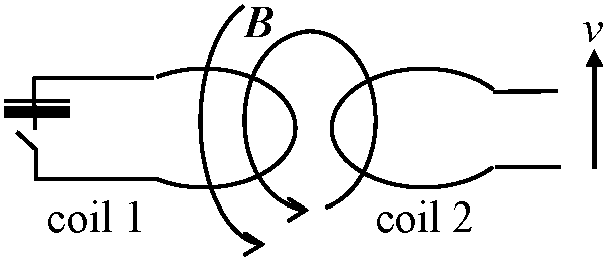
電磁誘導 → コイル1に流れる電流Iの時間変化dI/dtがコイル2に電圧Vを生じさせる → V2 = –dΦ2/dt → コイル2を貫く磁束が変化 → コイル2の両端に電圧V発生 Def. 相互誘導 mutual induction, M: 電圧の生じ易さ≡ コイル1に流れた電流が作る磁束がコイル2を貫く効率
F2 ≡ MI1 → V2 = –M·(dI1/dt)
V2 → 単位: ヘンリー(henry, H) (Henry, Joseph, 1797-1878) 相互誘導Mはコイル1と2の幾何学的配置(形・大きさ・位置)とコイル間にある物質の透磁率のみで決定 自己誘導 (自己インダクタンス) self inductance: コイルに流れる電流を変化させると、自分自身にも誘導が起こる
V = –dΦ/dt < 0 → 電流を大きくしていくと、自分を貫く磁束が大きくなる
Def. 相互誘導と同じに扱えるため Φ ≡ LI, 自己誘導 self induction, L (単位 = H), V ≡ –L·(dI/dt) > 0
微小変化に必要なエネルギーを求め0から最後の状態まで積分
μ: 透磁率 コイルの内部の磁場はアンペールの法則∫cB·dl = μIから 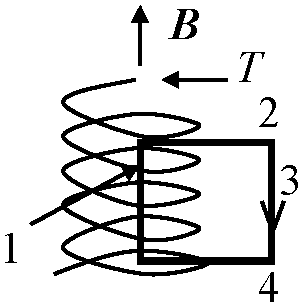
インダクタにアンペールの法則適用: 磁場の向きでコイルの内部のみに存在 → インダクタはその内側の空間Slにエネルギーを磁場として蓄えていることを表す フレミングの法則 Fleming's law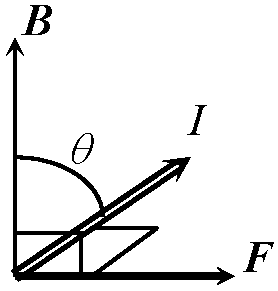 1. 左手の法則 left hand rules (左手のFBIの法則) = モータの原理
1. 左手の法則 left hand rules (左手のFBIの法則) = モータの原理
親指 = F (電流の受ける力), 人差し指 = B (磁場), 中指 = I (電流の向き) IL: 電流の方向を向いた長さILのベクトル 2. 右手の法則 right-hand rules = 発電機の原理Ex. 電磁血流計: 血管を露出させ、血管をプローブでくわえ込んで血管内の血流を計測
交流 alternating current, AC時間と共に変化する電圧(電流) ↔ 直流Ex. 交流発電機(オルタネーター) alternator: 永久磁石の作る磁場中で、コイルが回転する コイルが外力で回転 → 電磁誘導によりコイル両端に起電力生じる [角速度 ω]
磁場方向から回転コイルを眺める: コイル面積は大小変化し、コイルを貫く磁束量は時間と共に増減 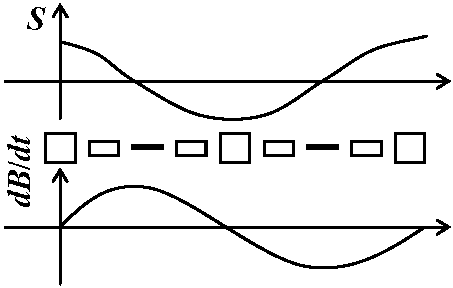 回転するコイルの導体中の電荷
回転するコイルの導体中の電荷→ 磁界中で運動しているのでローレンツ力を受ける 力の向きはコイル中、どこでも強めあう向きに生じる → コイル両端には電流を流そうとする力(起電力)生じる ローレンツ力の向きは時間と共に変化するので起電力の向きも時間と共に変わり、起電力は交流となる シンクロスコープ synchroscope (オシロスコープ oscilloscope): 電流等の変化を波形で表す観測装置 Def. 交流電圧(交流起電力): 回転するコイルに発生する起電力, V(t) = Vmsinωt [Vm: 最大電圧値, ωt ≡ 位相]抵抗を挟む → オームの法則 → V(t) = RI(t) → 電流発生 Def. 交流電流: 起電力が導線に流す電流, I(t) = Imsinωt, Vm = RImDef. 実効値 effective value: 抵抗負荷に供給した時に直流と同じ平均電力を発生した時の数値
Ve (実効電圧 effective alternating current voltage) = Vm/√2 → 最大値の1/√2 Def. 周波数, f = 1/T = ω/2π [単位: 1ヘルツ (hertz, Hz) ≡ 1 cycle/sec] → 東日本 50 Hz, 西日本 60 Hz 交流回路: → V(t) = Vmsinωt → I(t) = Imsin(ωt - φ) → 位相がずれる Def. φ ≡ 位相のずれDef. バンド(帯域) band: 周波数の範囲 Def. 発振器 oscillator: 特定周波数信号を出す装置 Def. インピーダンス impedance, Z = Im/Vm 変圧器(トランス) transformer: 相互誘導Mを持つ電気回路素子 → 電力損失少ない高圧送電可能 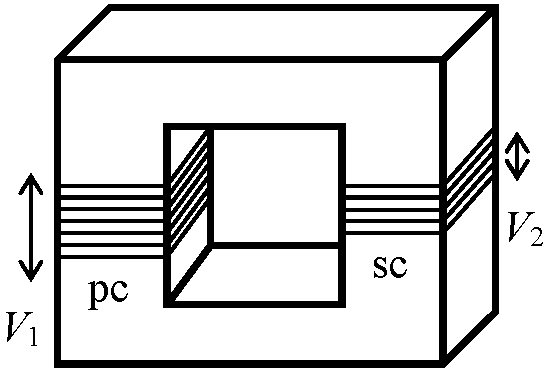
1次コイル primary coil, pc: 電圧V1をかける方のコイル, 巻き数 = N1 → 磁束φB発生 → 2次コイル secondary coil, sc: 巻き数 = N2
→ pc: 逆起電力Vr1発生 + sc: 誘導起電力V2発生 Ex. N2 > N1 → V2 > V1
→ pcとscの巻き数により電圧を調整できる = 変圧器 バイアス bias: 一定の値を加えることで入力信号をずらすこと グリッドバイアスgrid bias: 電圧の調整ボリューム
逆バイアス reverse bias: ダイオードに逆方向(電流が流れない方向)に電圧を加えること |
|
= マクスウェル関係式 変位電流: アンペールやファラデーら発見した電気・磁気法則 [次のことを説明できない] → マックスウェル完成 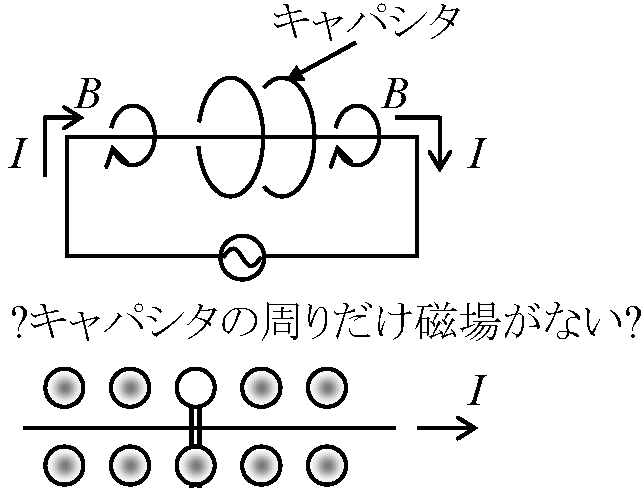 (電気)回路(ecelctric) circuitに電圧源をつなぐ
(電気)回路(ecelctric) circuitに電圧源をつなぐ
→ キャパシタが充電chargeされるまでは電流が流れる Q. 導線の周りには電流により磁場が生じる→ キャパシタによって導線が途切れている所はどうなる アンペールの法則 ∫cB·dl = μI → キャパシタの周りに磁場ができない⇔ 実際には磁場は生じる
電荷の移動によって変化する電場は、ガウスの法則 ∫E·ds = Q/ε によって決まる → 変位電流 displacement current: 電場変化として伝わる電流 → アンペール・マックスウェルの法則: アンペールの法則修正 – 変位電流を考慮した法則 ≡ 1/μ·∫cB·dl = ∂∫εE·ds/∂t + I マックスウェル方程式 Maxwell equations電気磁気法則をまとめ、4法則で全現象説明可能なことを示す4式
マックスウェル方程式電荷はあるが磁荷はないことを除き、電場と磁場が完全対称 symmetry→ 電束と磁束、誘電率と透磁率を入れ替えると電場と磁場が入れ替わる → 波動方程式: 式から電磁場が波動を生じることを数学的に導く 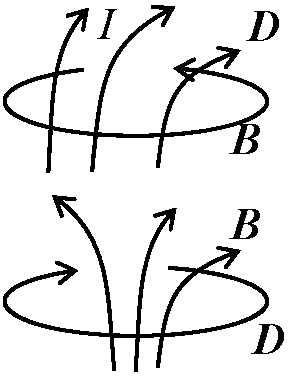
微分形でマックスウェル方程式を表す
1/μ·(∂By/∂y – ∂Bz/∂z) = ∂Dx/∂t + ix
1/ε·(∂Dy/∂y – ∂Dz/∂z) = ∂Bx/∂t [応用] 波動方程式: ∂2Ex/∂z2 = εμ·∂2Ex/∂t2, ∂2By/∂z2 = εμ·∂2By/∂t2 Ex. 波動方程式の解 – 電場・磁場の波動はマックスウェル方程式の解Ex = E0sin(wt – kz), By = B0sin(wt – kz), k = w√(εμ) 電磁波 electgromagnetic wave 存在理由(直感的理解)波は変化が有限な速さで、次々と隣へ伝わる時に生じる 電流の大きさや向きが時間と共に変化する時、電流の回りに磁場ができ、その磁場は時間的に変化 → 磁場変化は輪になった電場を周りに作る。電場変化は輪になった磁場を作る。電場が磁場を作り、磁場は電場を作り、鎖のようにつながり遠くへ伝わる → 電磁場の変化は波となり伝わる (= electromagnetic wave)
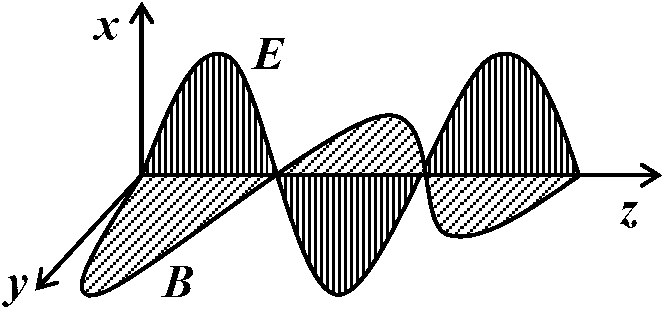
電磁波存在を示す実験Maxwell: 理論的に電磁波存在証明 → [存在疑問] 電磁波には明確な媒質がない
Ex. 波は海水を、音は空気を媒質とし伝播 ↔ 光は真空中伝播 → 光 ≠ 波動
ガラス瓶の裏表に金属箔を貼った発信器存在 → 金属棒(アンテナ)を付けると送信器transmitterになる
電波 radio waves: TV、ラジオ、衛星放送、レーダー、携帯電話、ポケベル、MRI、電子レンジ ホログラフィー holography: レーザー光線を利用した立体映像
紫外線 ultraviolet rays: 半導体デバイス製造 Ex. ミツバチ: 携帯電話電磁波 → (方向感覚狂わせ)最大70%の個体が巣箱に戻らない (現在否定的) 制動放射 breaking radiation (bremsstrahlun): 荷電粒子が電場により加速度を受けた時に放出する電磁波やその放射過程電磁波発生電磁場変化が波として伝る機構 = 波動になる理由Ex. 左で棒を上下 → 棒の変化は瞬時に右に伝わる ≠ 波動
左で紐を速く上下 → 紐の変化はゆっくり伝わり紐に波(波動)発生
記号表現: 電場∥紙面 ≡ 力線 |
電磁波の性質電磁波も、性質を決めるのは静電場・静磁場と同じく誘電率・導電率・透磁率平面波 plane electromagnetic wave: 電磁波発生源から無限に遠い時、電磁波の電場・磁場が共に進行方向に垂直になる電磁波 → 波の重ね合わせ superposition: 全電磁波は平面波重ね合わせで作ること可能 平面波の電磁場Ex = Axcos(kz – ωt), By = Aycos(kz – ωt)
Ex, By: 電場と磁場
位相 phase
波動パラメータ: λ (m) 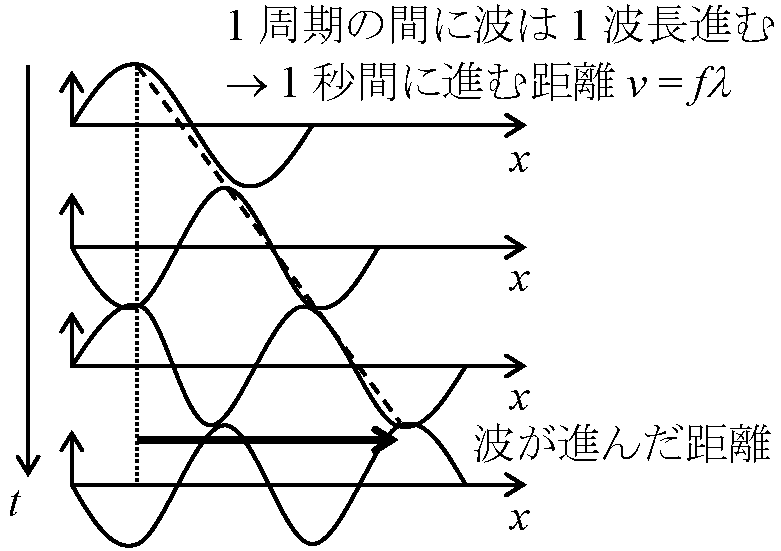 波の進む速さ speed of light: 周波数と波長により決まる
波の進む速さ speed of light: 周波数と波長により決まる電磁波の速さ = 光速: 電磁波の存在を示す波動方程式
→ ∂2Ex/∂z2 = εμ·∂Ex/∂t2, ∂2Hy/∂z2 = εμ·∂Hy/∂t2 Ex. 電場: k2Axcos(ωt – kz) = εμω2Axcos(ωt – kz) ∴ k2 = εμω2 v = fλ, f = ω/2π, λ = 2π/k ∴ c = fλ = ω/2π·2π/k = ω/k = 1/√(εμ)
実測値: 真空中の光速c (m/sec) 電磁波エネルギー電磁波のエネルギーが伝わる方向は電場とも磁場とも直角に交わる向き電磁波を説明する図はいつも、電場と磁場が直角に交わっていて、電場や磁場が向いている方向とはまた別の方向に電磁波が進んでいくように書かれる (理由略) → ポインティングベクトル pointing vector, S: S ≡ E × H → 電場や磁場が大ならより大きなエネルギーが移動 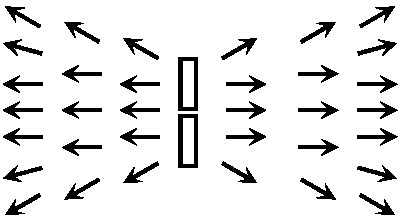
ポインティングベクトルはいつも電磁場のエネルギーが移動している向きを向く → ポインティングベクトルはアンテナから外向きを向く 応用 (1879 Edison: 電球発明)Ex. 豆電球に乾電池をつなぎ光らせた時、電線をつないだとき電線に電流が流れ、その周りに磁場が生じ、電池の電位差により電場が生じる。電位差は殆ど電球にかかるので、電線間にも電場が生じる → ポインティングベクトルの向きを考える。ポインティングベクトルは電磁場のエネルギーの流れを表す
乾電池に豆電球をつなぐと電流が流れる 電磁波の応用アンテナ(空中線) antenna, aerial: 電磁波を作る(送信)にも、電磁波を受ける(受信)にも使える
半波長ダイポールアンテナ: 最も簡単
進行波管 traveling wave tube: 中空の円筒で、電子を加速する部分。内部仕切があり中心に穴が開く |
有効電力 active power, P負荷で実際に消費される電力↔ 無効電力 inactive power, Q: 負荷と電源とで往復するだけで消費されない電力 (単位, バール var) 皮相電力 apparent power, S: 表向き(見かけ)の電力 → 電圧の実行値と電流の実効値との積
S = |V||I| = √(P2 + Q2), (単位, ボルトアンペア VA)
容量(性)リアクタンスcapacitive reactance
電気出力 electrical power 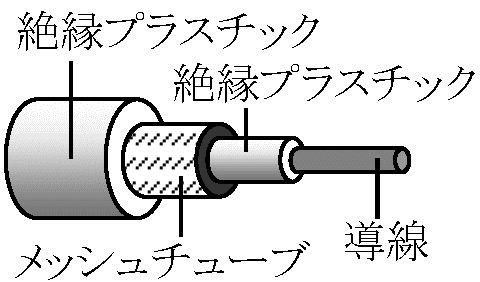 同軸ケーブル coaxial tube: 芯線(主, 銅線)を絶縁体で包み、その上を網状金属シールドで覆う多重構造ケーブル(通常、外側を塩化ビニール等で覆う = 補強)。ケーブル両端にターミネータ(終端抵抗)必要
同軸ケーブル coaxial tube: 芯線(主, 銅線)を絶縁体で包み、その上を網状金属シールドで覆う多重構造ケーブル(通常、外側を塩化ビニール等で覆う = 補強)。ケーブル両端にターミネータ(終端抵抗)必要
|
長所: 外部への電磁波漏れ少 = 外側電磁波の影響受けにくい → 網状金属シールドの機能
+ 高可塑性
→ TVアンテナ線、LANケーブル中10BASE-5や10BASE-2 + 1ヶ所の障害が全ラインに影響 + 配線等に変更があると作業面倒 ツイストペアケーブル: 絶縁体で覆う2本の電線をより合わせ対にしたケーブル
より合わせ = 外からの電磁波等の影響を抑え、ノイズ受けにくくする
通常の電気信号を利用したケーブルより速度大幅向上 = 高速大容量データ転送可能 |
[ 原子 ]
|
放出スペクトル(発光スペクトル) emission spectrum 吸収スペクトル absorption spectrum 光線 (light) ray輝線(スペクトル) emission line spectrum: 電磁波強くなっているスペクトル線↔ 吸収線(暗線) dark line: 吸収され弱くなっているスペクトル線 線スペクトル line spectrum → 連続スペクトル continuous spectrum可視光線 (400-760 nm) visible light: 可視光スペクトルvisible (light) spectrum → 可視光放射 visible radiation (光の)スペクトル spectrum (of light)
色のスペクトル color spectrum
- 赤外線放射 infrared radiation ビーム(光束) beam
コヒーレント光 coherent light: 光束内の任意の2点における光波の位相関係が時間的に不変で一定に保たれ、任意の方法で光束を分割した後、大きな光路差を与えて再び重ねあわせても完全な干渉性を示す光 - 自然界には存在しない 白熱球(白熱ランプ) incandescent lamp (light) (白熱 incandescence, adj. incandescent 白熱の) X線
連続X線 continuous X-rays 吸収スペクトルabsorption spectrum |
光量子束密度 photon flux density, PFD太陽光特性 = 波動・粒子性光合成光量子束密度, PPFD (μmol/m²/s)∝ 光量子(光子)個数光合成で使う400-700 nmに含まれる単位時間、単位面積あたり光子数
速度計算ではPARより便利
E: 光子1個の持つエネルギー Q. 波長300 nm(紫外線)と700 nm(可視光赤色)の光量子1 molのエネルギー A. E300 = h × c / (300·10-9) × N = 399 kJmol-1 __E700 = h × c / (700·10-9) × N = 171 kJmol-1 6CO2 + 6H2O + [Energy] → C6H12O6 + 6O2
1mol C6H12O6固定: E = 2881 kJ 必要 放射照度(放射束密度) irradiance, II = PFD × NA × E = PFD × NA × hc/λ各波長エネルギー強度積算値 W/m² = J/m²/s, 非SI系 cal/cm²/min
名称: 積算波長範囲 測定対象物からの光(電磁波)の分光放射エネルギーを測定する計測器
Ex. 太陽放射波長毎の放射エネルギーを測定 |
電磁波のうち、ヒトの目で見える波長
生活における光照度 illuminance, lux (lx)比視感度曲線に合わせた明るさ単位
視感度: 目は黄緑(≈ 555 nm)付近の光感度良く、緑波長から離れるにつれ感度下がる 網膜視細胞: 錐体(明所) + 桿体(暗所) ⇒ 比視感度曲線は2種類 光束 luminous flux単位時間あたりエネルギーを視感度で補正単位: lumen (lm), 1 lx = 1 lm/m² 光度 luminous intensity光源からの立体角あたりの光束単位: candela (cd), 1 cd = 1 lm/sr2 |
輝度 luminance光度を光源の面積で割った値単位: ニト (nt), 1 nt = 1 cd/m2 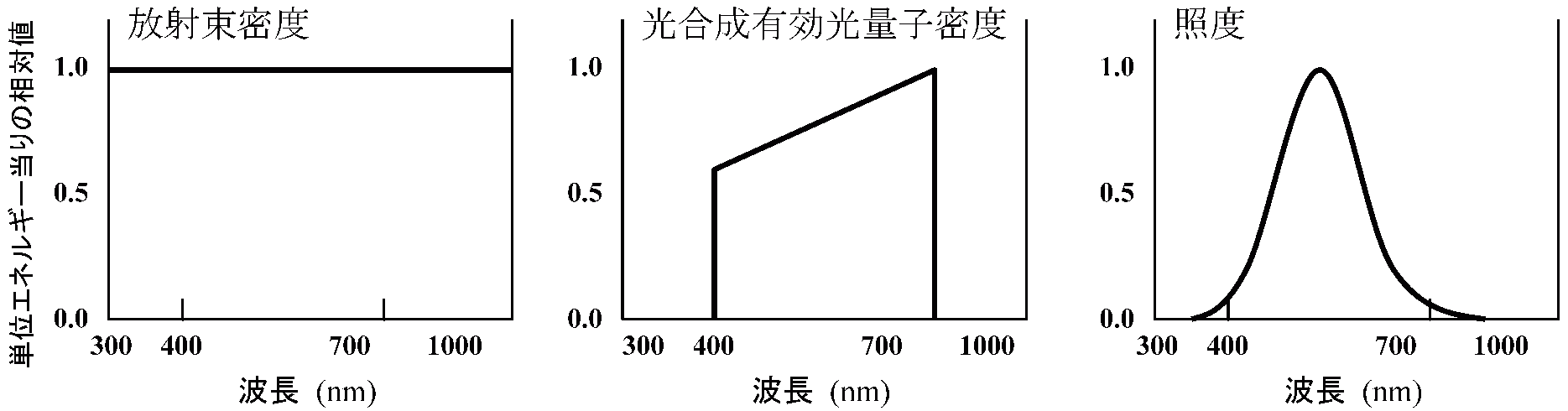 図. 各波長における単位エネルギーあたりの感度の相対値 (林 1966) 光合成有効放射 (PAR) - 光合成 (photosynthesis) 光合成利用波長400-700 nmの光 地上到達太陽光の45% = 450 (PAR, W/m2) / 1000 (地上到達光) × 100 |
波長の定義(10-400 nm)区分 (nm): 生物学的 vs 人体影響 → オゾン層の効果UV-C: 100-280 vs < 290 → 透過しない UV-B: 280-315 vs 290-320 → オゾン濃度に依存 UV-A: 315-400 vs 320-400 → 殆ど吸収しない
生物学的区分: 第2回国際光線会議で提案された区分
図. 日本における紫外線分布 (kJ/m²) |
紫外線量に影響を与える因子波長 (μm) ___ 吸収機構< 0.1 _______光電離作用 (160 km) → 電離層形成 0.1-0.2 _____ 酸素の光解離 photodissociation (110 km) 0.2-0.3 _____ オゾンの光解離 (40 km)
太陽高度・緯度・季節・時刻 |
|
放射線と物質の相互作用を研究 Def. 核分裂(nuclear) fission: 原子核が2つの原子核に分裂する現象(核反応 nuclear reaction) 天然原子核: 約265個 = 安定 ↔ 人工原子核(数千個存在) = 殆ど不安定 不安定原子核 → [原子核外に粒子や電磁波放出 ≡ 放射線 radioaction] → 安定 Def. (化学) 超ウラン元素 transuranium elements: ウラン原子番号92より原子番号の大きい元素原子番号95以降の元素 = 基本的に人工的に作る → 人工元素 全て放射性 → 半減期は地球年齢より超短い = 元素が地球誕生の頃に生成されても既に消滅 Ex. 超ウラン元素: 原子炉や粒子加速器で人工的に作られたもの Def. (原子核)崩壊(壊変) (nuclear) decay: 元原子核(親核 parent nucleus) → 別原子核(娘核 daughter nucleus)不安定なら娘核も崩壊 → 崩壊は安定な原子核に到達するまで続く (燃料)親物質 fertile material: 中性子捕獲し核分裂性に変化する物質Ex. U238, Th232 核分裂性核種 fissile nuclide: 中性子入射により核分裂を起こす核種
→ 親物質核 fertile nuclide → 娘核種 daughter nuclide 自然核分裂 spontaneous nuclear fission Law. 放射性崩壊の法則: 放射線種に関わらず成立N(t): 任意の時刻tにおけるある放射性原子核の個数 dN: dt時間内の崩壊数 -dN/N ∝ dt ⇒ λdt = constant 初期時刻原子核数, N0 → N(t) = N0eλt新しく生成される娘核の個数 Nd → Nd = N0 – N(t) = N0(1 – eλt) Def. λ: 崩壊定数 decay constant → 特定の崩壊に固有な定数
T, P等の巨視的条件や、化学結合のような原子核外の微視的環境には基本的に非依存 → 崩壊定数λと逆数関係 Def. 半減期(放射性半減期) half-life, T1/2 = ln2/l ≈ 0.693/λ = 0.693τ
→ τに比例 核エネルギー nuclear energyDef. E = mc2 ⇒ 原子質量減少(= m↓) → E変化 [別エネルギーとして放出 ≡ 核エネルギー]原子核反応: 原子の質量が変化する反応 ⇒ 核融合 (nuclear) fusion ↔ 崩壊(核分裂) Ex. 1 kg↓, c ≈ 3 × 108 (m/s) ⇒ (3 × 108)2 = 9 × 1016 Jのエネルギー発生 核反応式 (核方程式) nuclear equation核融合: 4H+ + e- → 1He2+ + 2ν[⇒ 水素原子核 × 4 + 電子 × 2 → ヘリウム原子核 + ニュートリノ × 2]
核変換 nuclear change
→ 6.2 × 1014 Jエネルギー放出 レーザー核融合 laser fusion: (人工的)レーザーエネルギーによる核融合 Def. 崩壊熱 decay heat: 放射性物質radioactive material崩壊での放出放射線エネルギー約200 MeV/(1核分裂)の莫大なエネルギー放出 中性子・陽子・γ線、β線を原子核に入射 → 原子核が励起 excitation され核分裂容易になる
核分裂生成物 fission products, FP: 核分裂で生じる核種 + 一連の放射性崩壊radioactive decayでの核種 遅発中性子先行核 delayed neutron precursor: β崩壊による娘核が中性子を放出する核種 Ex. Br88, I137 核分裂片fission fragment: 核分裂でできる2つの原子核低エネルギー中性子による核分裂では重いものと軽いものの2つに分かれる場合が多い (E: エネルギー) 結合エネルギー binding energy結合した状態と解離した状態のE差 (1 ≠ 2)1. 全結合エネルギー bond dissociation energy: 全核子解離に要するE 2. 核子の結合エネルギー bond energy: 核子1個分離に要するE |
核分裂エネルギー fission energy: 核分裂時に放出されるE
エネルギー部位 値(MeV)
2個の核分裂片の運動エネルギー ca 160
即発γ線 7
中性子 ca 5
核分裂生成物の壊変により放出されるβ線 ca 8
核分裂生成物の壊変により放出されるγ線 ca 7
中性微子 12
計 = 1回分の核分裂当たり ca 200
Def. 放射線の強さ: 物質中のある放射性核種が単位時間内に崩壊を起こす回数(能力または活性度) → 物質中に含まれる放射性核種の量と半減期により決まる = 発生源の放射線の強さ A(t) ≡ dN(t)/dt = λN(t) = λN0e-λt ⇒ 一般に時間tと共に変化 (特に断らない場合はt = 0の値) Bq (ベクレル, bequerel): 国際単位SI系1 Bq = 壊変率毎秒1個(disintegration per second, dps)の放射能 Ci (キュリー, curie): 毎秒壊変数3.7 × 1010 (現在補助単位)1 gのRa-226の放射能量を基準 連続放射性崩壊崩壊系列 (nuclear) decay series1. 1系列: 核種a → [崩壊] → 核種b → … → c (安定)
(核分裂)連鎖反応 (fission) chain reaction dNa/dt = λaNa, dNb/dt = λbNb + λaNa, dNc/dt = λbNb ⇒ Na(t) = N0eλat, Nb(t) = (λaN0/(λb – λa))·(eλat – eλbt) 2. 複数の放射性崩壊(拡張)仮定: 崩壊様式a, bの崩壊定数がそれぞれλa, λb, 崩壊定数λeffをもつ単一の崩壊様式 dN = λaNdt – λbNdt ≡ λeffNdt ⇒ λeff = λa + λb, 1/τeff = 1/τa + 1/τb, 1/Teff = 1/Ta + 1/Tb → τeff = τaτb/(τa + τb), Teff = TaTb/(Ta + Tb) 3つ以上の崩壊様式がある場合にも同様な関係式が導かれる 崩壊型 type of decayP, proton. N, neutronα崩壊 α decay: 一般に質量数の大きい核で起こる → α線放射 (α radiation) = ヘリウム原子核放出過程 β崩壊 β decay: 負のβ崩壊(β崩壊, s.s.) + 正のβ崩壊 + 軌道orbital電子捕獲→ β線(β ray)放射(β radiation): β粒子(β particle) = 電子流 1) 負のβ崩壊(β-崩壊): 一般に、中性子数が陽子に比べ多過ぎると起こる原子核内中性子が陽子に変換 → 電子と反中性微子ν- (反ニュートリーノ anti-neutrino)原子核外放出 2) 正のβ崩壊(β+崩壊): 一般に、陽子数が中性子に比べ多過ぎると起こる原子核内の陽子が中性子に変換 → 陽電と中性微子ν (ニュートリーノ neutrino)原子核外放出 3) 軌道電子捕獲 electron capture, EC: 原子核がその軌道電子を捕獲吸収し原子核内陽子が中性子に変換
↔ β-+崩壊: 電子や陽電子が原子核から放出
放射性核種の原子核から放出される電磁放射線(電磁波の1種) 散乱 scattering粒子が衝突した時 →
放射線 (radiation, radial rays)= 粒子放射線 + 電磁放射線
一般に「放射線」というと、高エネルギー電離放射線の方を指す 電離放射線: 物質を通過する際か間接にその物質の原子を電離するエネルギーの高い放射線 非電離放射線: 電離放射線でないもの線量 dose物質に照射された放射線の化学的あるいは生物学的効果を定量的に評価する放射線量照射線量(放射線量) exposure dose: 照射された放射線の質 レントゲン単位: X線やγ線 吸収線量 absorbed dose: 物質が吸収した放射線量 → 放射線照射で引き起こされる化学的又は生物学的効果は照射線量ではなく、吸収線量で決まるラドrad単位, グレイGy単位(SI 単位系) 1) 電離作用による検出器
電離箱 ionization chamber: 密閉箱中に2つ電極を置き、放射線電離作用でできた箱中のイオンを電極に集め電極間に流れる電流から放射線強度を知る
シンチレーションカウンター scintillation counter Ex. フィルムバッチ: 荷電粒子が写真用乳剤中を通過時に化学変化を起こす現象(写真作用)を利用 |