水文学

(2014年8月23日更新) [ 日本語 | English ]

水文学 (Hydrology)

有珠山 / サロベツ泥炭採掘跡
1986年, 2006年の有珠山火口原. ワタスゲ・エゾカンゾウ

HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 水文学

陸域の地表と地表付近の水動態を研究 (水循環対象とする地球科学一分野)
↔ 観測流域データ取得が必要な地球物理学・地理学に起源した野外科学
→ 陸域における水循環過程を明らかとする科学

国外: 各国水文気象局による河川流量の定常観測を含める(s.l.)
日本: 降水precipitationや蒸発evaporation、流出runoffの時空間分布の統計的性質や力学的特性解析分野

→ 現象の分類: 蒸発生起過程、積雪・融雪過程、地表面浸透過程、表面流出発生過程、土壌内の浅い地中水流動過程、基盤に沿う地下水の流動・貯留過程等

→ 対象や行政的要請による分類: 山地(森林)水文学、農地水文学、河川水文学、地下水水文学、都市水文学

地域の気候条件

熱帯水文学: 雨期、乾期蒸発散量解析から、河川水等の季節変動に注目
寒冷圏水文学: 積雪や土壌、河川凍結・融解という現象を取り扱うため、大気と地表間の熱交換過程を含む
湿潤地水文学: 水資源の必要性から、降水量が潜在的蒸発量より多い地域
乾燥地水文学: 少ない地域
水質水文学: 流量に加え、河川水や地下水の水質形成とその流下過程での変質を取り扱う
同位体水文学: 水や酸素の安定同位体から水の循環過程を対象

[ 水循環 | 水 | 湿原 | 海草 | 海洋生態学 | 土壌 ]

河川 (rivers and streams)

河 + 川 = 両者をまとめて河川とする
慣用英語: stream < riverのサイズ関係 (小川 brook は文学的、論文ではまず使わない)
科学用語: 両者に厳密な境界や区別なし

大河川でもstreamを使うし小河川でもriverを使う
河川 = running water: サイズを考えなくてよい便利な言葉

水に関する理論: 保安林思想・洪水と渇水

水文 = 水を力学的に扱う
水理 = 水を量的に扱う
資料調査
面積降水量の計算: 等雨量線法、ティーセン法、支配圏法、算術平均法
洪水流量推定法: 既往最大流量か確率洪水流量利用法、公式法、単位流量図法(ユニットハイドログラフ)
流量測定法: 流速法: 流速分布、測定法。量水堰法: 刃形堰、広頂堰。洪水位痕跡法
平均流速公式: ジェジー型公式、指数型公式

[ 物質循環 ]

水循環 (water cycle)

蒸発 → 降水 → 流出 → 蒸発 (循環)
地球温暖化による水循環変動 → 各国水文気象局定常観測データ利用可能
広域地表面となる大河川も対象
全球気象観測データを使った数値気象(気候)モデル

2.5-1° (250-100 km) 格子点に補完された気象データから大気水蒸気収支 → 全球降水データ併用し降雨余剰量(降水量-蒸発量)月単位算定

被覆流域蒸発散量: 森林 > 裸地・草地 → 多くの観測流域結果から判明

評価は想定する地表面のスケールにより異なる
Ex. 日本(島国): 高蒸発量 = (流出安定に寄与 vs 河川流出量低下)

Ex. ユーラシア大陸(大スケール): 海洋上から運ばれる水蒸気が陸域降水の最初の湧源だが、大陸内部では地表から蒸発した水蒸気が次の降水の湧源に加わり、蒸発量の多さは降水量増大となる
地域的降水量変動は、地球温暖化の影響のみでなく、林地?農地転換等の土地利用改変も影響

メカニズム解明: 蒸発散過程、土壌水分状態と蒸発量の関係等の一般化・モデル化、求められる

水利用増大による河川水・地下水汚染各地で進行
防止法策定や、水生生物や自然環境への評価を含む水利用対策必要

水収支 (hydrological balance)

1) 水収支 hydrological balance

水循環において、ある水システムにおける単位時間での水の流入量と流出量
Def. 滞留: (水が)一箇所に滞ること
Def. 滞水(滞留水): 流れずに一箇所に滞る水

水界生態系の構造を決める上でも重要

Def. 滞留時間 residence time:

Ex. ダム: 流れダム ↔ 止まりダム(独自のプランクトン発生)

入替時間 turnover time, τ₀ = S/Q

S: 貯水量
Q: 通過フラックス

Def. 保水機能: 雨水を地中に浸透させ、または一時的に滞留する機能

2) 水文基本操作

集水域 catchment: 支流を含む1河川(a river and the tributaries)の全域(山頂から海岸まで)
流量 discharge: 単位時間あたりに流れの断面を通過する量 (Ex. m³/s)

計画規模: 治水計画策定にあたり、どの程度の規模の洪水まで安全を確保するかという目標

Ex. 計画規模 1/100 → 100年に1度起こりうる規模の洪水を想定
閾値 threshold: その現象を起こさせるに必要な最小エネルギー → 洪水規模の限度

基本高水流量 basic high water discharge: 河川が洪水調節を行われない状態での高水流量

→ 流域に降った計画規模の降雨(時間当りの降雨量等から決める。通常は100-200年に1回の割合で発生する洪水を想定)がそのまま河川に流れ出た場合の河川流量。基本高水流量は、この流量がハイドログラフに示される最大流量から決定された値

計画高水流量 estimated high water discharge = [基本高水流量] - [各種洪水調節施設洪水調節量]

流出量 runoff: 融雪水を含む(1集水域での)流量を時間で積分したもの
山地降水量換算: 観測点が多いほど精度増 water balance

単純平均法: 各地の降水量観測値の算術平均
等雨量線図法: 観測値から等雨量線図作成 → 線間の面積 = 荷重 → 各帯降水量の加重平均値求める
スイーセン法 Theissen method: 観測点を結び出きる三角形の外心求め、外心を結び出きる多角形面積を重さとした加重平均値を求める

water balance
実動流量と平均

降水量 ↔ 流出量 ↔ 流出率

降水量-流出量は地域毎に普通相関あるが、同一地域でも期間により回帰係数異なる
流出率(流出係数) = 流出量/降水量 → 年差あるが一定と仮定すること多い

3) 森林量水試験

水循環過程を知ることが目的 → 長年月の観察必要

単独法: 1個の流域において森林伐採後の水文量を比較する

併行法: 林相の異なる2個以上の流域の観測値を比較する

対照流域法: 初めの林相がほぼ同一である2個以上の流域において前期観測期間の観測に基づき気象要素の影響による(森林の影響によらない)流出量変動を求めておき、対照となる流域以外の森林にある種の処理(Ex. 伐採)を加え、ついで後期観測期間の観測を待って森林の影響を検出

水年: 水文統計便宜上設定する1年

Ex. 積雪地方: 積雪前適当月から。無積雪地方: 最低降水量月から

4) 蒸発散 evapotranspiration

L = P + R
L = E + T

L = loss (損失量)
E + T ≡ evapotranspiration (蒸発散量)

降水量豊富である日本では年蒸発散量変動は一定とみなせることが多い
蒸発散位: 植生のある土地に水を十分供給 → 起こりうる最大蒸発散量

5) 遮断・浸透・貯留

地下水 groundwater: 土壌水が飽和状態で存在する亜表層水(地表面に現れれば表層水と同じ)

地下水位 groundwater table: the upper limit of the groundwater
高位水位 perched water table: 地下水等の土壌水の上限の水位

粗度係数 roughness coefficient: 流水の流れやすさ表す地表面粗さの度合
a) Def. クローネ遮断 (I, crown interception): 降水の一部が植物に付着しそこで蒸発し林床に到達しないこと = 水平遮断

I = grossP - netP (grossP: 全降水量 netP: 林内降水量)

netP = Sf + (Th + Dr)

(Sf: 樹幹流下量 Th: クローネ通過量 Dr: クローネ滴下量)

∴ I = grossP - Sf - (Th + Dr)

強度がiである降水がT時間続いた時

クローネ遮断率(%) = I/(iT) × 100
水平遮断率(露滴補足): 霧が水平に動く途中森林により取られられる率

b) Def. 浸透 infiltration: 水が土地表面から染み込むこと
透水 percolation, mm/hr: 土層内での水の移動
浸透強度 infiltration intensity, mm/hr: 水が土地表面から単位時間あたりに透水する量

透水強度 percolation intensity, mm/hr: 地中における一断面を単位時間あたりに通過する水量
透水能 infiltration capacity, mm/hr: 浸透強度の最大値
降雨余剰 rainfall excess - この分が表面流出量と考えられる

= i - f (i > f) (i: 降雨強度 f: 土壌浸透能)

c) Def. 流出 runoff: 降雨や融雪水が地表を流れること

表面流出(直接流出): 地中に浸透せず流出 ↔ 地下に浸透した後に流出

ハイドログラフ(量水曲線、時間流量曲線) hydrograph: 水利特性(流量、水面高、水位、流速等)-時間関係図

洪水曲線 storm hydrograph: ハイドログラフ中で特に洪水時のもの
water balance

河況係数 river regime coefficient: 1年中の最大流量と最小流量の差

係数大 ∝ 渓流的
ダム建設: 河況係数低下目的 - 上昇することがある

係数低下 - 河川安定 - 多様性低下

Law. 基底流量逓減の法則: 表面流出量と地下水流出量の分離、地下水流出量のみからなる無降雨日の流出量に適応される法則

Q₀: 初日の流出量 Q_t: t日目の流出量 a, c, K, β: 定数

a. Q_t = Q₀e^-et
a'. Q_t = Q₀K^t (K < 1) → K: 逓減比(depletion ratio)
b. Q_t = Q₀t - a (t ≠ 0)
c. Q_t = Q₀e^-ct
d. Q_t = Q₀/(1 + β(√Q₀)·t)²
日流出量がQ₀である日以後、流出量がなくなるまで降雨がなかったと仮定した時の全流出量は

SR = ∫₀^∞Qtdt = ∫₀^∞Q₀K^tdt = -Q₀/log_eK,

K: 蒸発散量最小時の値 → 式から地下水重力貯留量推定可能

氾濫シュミレーション: 越水や破堤が発生した時に河川より溢れた水が広がる様子をシュミレーションしたもの

氾濫挙動(浸水範囲や浸水深)を経時的予測できる

Tank model
もっとも単純なもの

タンクモデル tank model

貯留関数型の物理モデル (菅原 1972)
一般に長期流出に有効 → 地下水の流況解析・水質解析にも利用

q =λh … 流出流量-貯留高関係式
dh/dt = R - q … タンク内の水の連続式

→ R = 0 (降水なし)の場合

dh/dt = -q = -λh

→ 解(積分すればよい)

h = C·exp(-λt)
q = C·exp(-λt)

タンクを多段あるいは流出穴を複数にする → 直接流出と基底流出を同一のモデルで表現可能
有効雨量を用いなくてよい(観測雨量をそのまま用いる) 問題パラメータ設定に労力、工夫、経験必要

流出モデル

流出計算

流出解析
流出モデル

• 応答モデル(解析的モデル)

線形モデル: 単位図法(総合単位図法, 流出関数法, 等)
非線形モデル

• 集中定数モデル(変数 = 時間): 貯留関数法, 準線形貯留型モデル, タンクモデル, 等
• 分布定数モデル (変数 = 時間, 空間): Kinematic Wave法(等価粗度法), Dynamic Wave法
合理式法(合成合理式法) = 単位図法 + 合理式

流出モデルの同定: 実績洪水の再現
検証: 再現性・モデルの安定性

流出予測
基本高水の算定
流域将来像: 土地利用情況等の比較検討と総合治水対策評価のための流出量算定
比較の基本的視点 = 評価項目

流出予測への適応性: 「総合治水対策の比較・検討と評価」及び「流域の土地利用形態(流域将来像)に即した流出量の比較・検討」に適用可
同定での再現性: 実績洪水(観測洪水)を実用的に要求される再現精度でモデル定数を同定可
1. 同定の精度: 観測誤差等を含む実績洪水データを用いても実務的・実用的精度でモデル定数を同定可
2. 複数地点での再現: 基準点および対象流域内の(複数の)洪水観測地点で実績洪水を再現可
3. 解の安定性: 同定したモデル定数が安定 → モデル定数の小さな変化が流出量算定値の大きな違いにつながらない
検証での再現性/流出モデルの信頼性: 同定されたモデルにより(同定に利用した以外の)実績洪水が実用的に要求される精度で再現可
信頼性: 同定モデルにより(同定利用外の)実績洪水が実用的に要求される精度で再現可
流出解析・流出予測の計算効率: 計算処理等が、実務上、効率的
モデルとデータの整合性: モデル構造・システムと観測データの質量との整合性 → モデル構造が複雑・多層なためデータの質量不足する、逆に、モデル構造が単純すぎ既存データを活用できないということがない

[ 物理学 | 災害科学 | 水移動 ]

連続体力学 (continuum dynamics)

物体を巨視的にとらえ、物体の変形や流動、力学的波動を扱う物理分野
連続体: 変形する連続する物体 = 固体 + 流体 + 気体

固体力学 (dynamics on solid body)

固体の弾性と可塑性(塑性) elasticity and plasticity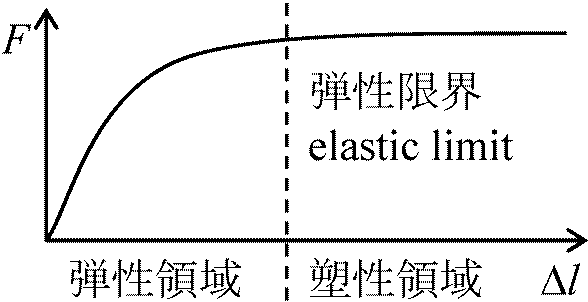

固体内部での力や変形 → 破壊, 変形

Ex. 切り欠けがあると切れ易い → 応力の集中や亀裂
変位displacement連続 → cp. 流体力学
楔 wedge: V字形の木(金属)片。木や石の割目に打ち込み割ったり物を押し上げたりするのに使う

Def. 復元力 restoring force: 自然長から伸ばしたり縮めたりして変形させると元の長さに戻ろうとする力
Def. (金属)疲労 fatigue: 強度より小さい繰返し応力による破壊
Def. 完全弾性体 perfect elastic body: 外力を取り払った後に完全にもとの体積と形に戻る 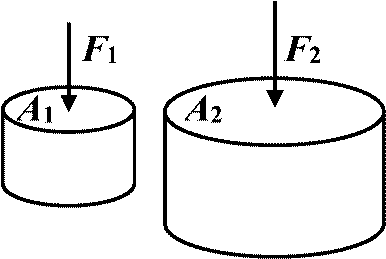solid

⇔ 可塑体(塑性体 plastic body): 外力で破壊こそしないが永久に形を変えてしまう
多くの物体は、この間の特性を持つ

大きさの異なる2つの物体 A₁, A₂

→ 破壊生じる荷重
→ F₁ < F₂ → F₁/A₁ ≈ F₂/A₂
→ 力を断面積で割った値が破壊には重要

Def. 応力 stress: 面のある方向に働く単位面積あたりの力 (通常外力に応じる形で発生)
= 圧力と同じ次元(力÷面積) Ex. N/m³, Pa = テンソル solid

3つの主要軸 principal stresses: 最大 + 最小 + 中間主応力
→ 全大きさが等しければ球 = 風圧 confining pressure

力をF → その面に垂直な方向と平行な方向にFを分ける:

F_N ≡ 鉛直力, F_S ≡ 剪断力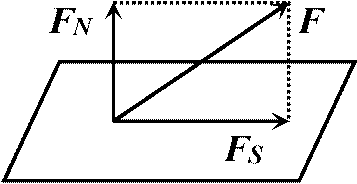

S: 断面積
Def. 法線応力(鉛直応力) normal stress, σ =

lim_S→0(F_N/S): 面に垂直な方向の応力

Def. 剪断応力(ずれ応力) shear stress, τ =

lim_S→0(F_S/S): 面に平行な方向の応力
極限: ある点で定義する → 応力が断面一様なら極限不要

直交座標系: 応力を成分表示
固体をX面(法線がx軸となる面）で切断。力Fのx, y, z成分をF_N, F_{S_y}, F_{S_z}
    σ_x = σ_xx = limS→0(F_N/S), τ_xy = σ_xy = limS→0(F_{S_y}/S), τ_xz = σ_xz = limS→0(F_{S_z}/S)
Y面で切断:
    σ_y = σ_yy = limS→0(F_N_'/S), τ_yz = σ_yz = limS→0(F_{S_z}_'/S), τ_yx = σ_yx = limS→0(F_{S_x}_'/S)
Z面で切断:
    σ_z = σ_zz = limS→0(F_N_''/S), τ_zx = σ_zx = limS→0(F_{S_x}_''/S), τ_zy = σ_zy = limS→0(F_{S_y}_''/S)
→ 9個の応力を任意の点で定義 = 9成分存在 → 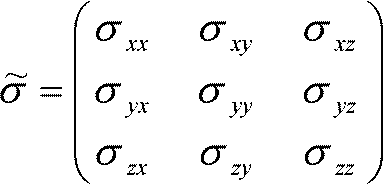solid

2階のテンソル (cf. ベクトル: 1階のテンソル)
符号に任意性 Ex. 鉛直応力: 引張応力+ ↔ 圧縮応力- (逆も可)

σ_x = σ_x(x, y, z) →

∂σ_x/∂x = lim_dx→0σ_x(x + dx, y, z)/dx = σ_x(x, y, z) + (∂σ_x/∂x)dx

Def. 接線応力 tangential stress: 接線方向への応力

展張(引張)応力 tensile stress ↔ 圧縮応力 compressive stress

Ex. 棒を引っ張る場合: 引張り強さ tensile strength
solid
solid F₁ = Fsinθ, F₂ = Fcosθ S_ABsinθ = S
∴ S_AB = S/sinθ
σ_⊥ = Fsin²θ/S = Ssin²θ
σ_II = Fcosθsinθ/S

= 1/2·Fsin²θ/S
= S/2·sin²θ

σ_⊥: 張力(外向きの力) tension, 圧力(内向きの力) pressure
σ_II: 剪断応力

張力・ずり応力: 面の方向により変化する → 非等方的・異方的
静止流体: ずれ応力 = 0, 圧力 = 等方的

歪(ひずみ) strain

無限 → のび(縮み) elongation, ずれ shear, 体積歪 volume strain
歪(ひずみ) strain, distortion: s^~ テンソル → 外力が働いたときに起こる長さ、体積等の形状の変化

変形体 deformable body: 変形(歪)deformationした形
強化 reinforcement: 変形抵抗を増し強度を上げること

変位: 変形前(x, y, z)座標にあった点 →

変形後(x + u, y + v, z + w)になる → 変位 ≡ (u, v, w) → 長さ次元

歪: 単位無次元

solid
変形前 A, B → 変形後 A', B'
AA'の変位 = (u, v, w), BB'の変位 = (u + du, v + dv, w + dw)
→ u, v, wはx, y, zの関数でありかつ連続で微分可能
du = (∂u/∂x)dx + (∂u/∂y)dy + (∂u/∂z)dz
dv = (∂v/∂x)dx + (∂v/∂y)dy + (∂v/∂z)dz
dw = (∂w/∂x)dx + (∂w/∂y)dy + (∂w/∂z)dz
この9つの偏微分が解ければ、あらゆる点の変位も求められる

Def. 垂直歪(縦歪) → εx = ∂u/∂x, εy = ∂v/∂y, εz = ∂w/∂z

ε = εl/l:ε = 1 → 2倍に伸びる (ε = -1 実現不可能)

Def. 剪断歪 shear strain →

γ_xy = ∂v/∂x + ∂u/∂y, γ_yz = ∂w/∂y + ∂v/∂z, γ_zx = ∂u/∂z + ∂w/∂x

変形前ABDC → 後AB'D'C' (A点変形後移動 → 平行移動させA点に置く)

solid
∠BAB' = θ₁, ∠CAC' = θ₂ → BB' = v(x + dx, y, z) – v(x, y, z)

tanθ₁ = BB'/AB = (v(x + dx, y, z) – v(x, y, z))/dx
∴ tanq₁ ≈ q1(if q₁ = minute) = ∂v/∂x
同様にq₂ = ∂u/∂y

∠CAB: 変形によって直角からθ₁ + θ₂ = ∂v/∂x + ∂u/∂y = τ_xy減少
→ τ_xy(剪断歪): 変形前直角 → 変形で生じた角度変化をラジアン表示

(τ_yz, τ_zx)も同様

Def. 回転: 2ϖ_x = ∂w/∂y – ∂v/∂z, 2ϖ_y = ∂u/∂z – ∂w/∂x, 2ϖ_z = ∂v/∂x – ∂u/∂y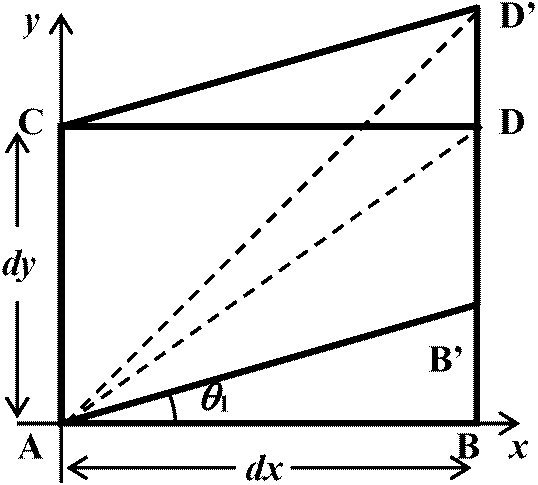
solid

q₁だけを考える → S(ΔADD') = S(ΔABB')
∴ |AD||AD'|sinΔDAD' = |AB||AB'|sinθ₁
→ |AD||AD'| = |AD|², |AB||AB'| = |AB|² → |AD|² = 2|AB|²
∴ ∠DAD' = 1/2·θ₁

同様にθ₁に対し行う

z軸のまわりの回転角 ϖ_z = ∠DAD'

= 1/2·(θ₁ – θ₂) = 1/2·(∂v/∂x – ∂u/∂y)

回転: 変更後に正方形の対角線が反時計回りに回転した角をラジアン表示

x, y軸まわりの回転: ϖ_x = 1/2·(∂w/∂y – ∂v/∂z), ϖ_y = 1/2·(∂u/∂z – ∂w/∂x)

偏微分の9成分: ϖ_x, ϖ_y, ϖ_zを除くε_x, ε_y, ε_z, γ_xy, γ_yz, γ_zxは固体に歪み

→ 歪(6成分): 3つの変位から求まり、6個を決定する適合条件式存在
仮想的球(外力0) → 外力を受けると楕円体に歪む

歪に[a, b, c (3) + その各々の方向 (3)]の6つの量がある

歪の適合条件式(6方程式)

独立ではない
満足すれば変位u, v, wは連続で微分可能

∂²ε_x/∂y² + ∂²ε_y/∂x² = ∂²γ_xy/(∂x∂y)
∂²ε_y/∂z² + ∂²ε_z/∂y² = ∂²γ_yz/(∂y∂z)
∂²ε_z/∂x² + ∂²ε_x/∂z² = ∂²γ_zx/(∂z∂x)
2(∂²ε_x/∂y∂z) = ∂/∂x(–∂γ_yz/∂x + ∂γ_zx/∂y + ∂γ_xy/∂z)
2(∂²ε_y/∂z∂x) = ∂/∂y(∂γ_yz/∂x – ∂γ_zx/∂y + ∂γ_xy/∂z)
2(∂²ε_z/∂x∂y) = ∂/∂z(∂γ_yz/∂x + ∂γ_zx/∂y – ∂γ_xy/∂z)

Pr. 歪の定義式を代入
Ex. 1. ∂²ε_x/∂y² + ∂²ε_y/∂x² = ∂²γ_xy/(∂x∂y)

∂²ε_x/∂y² = ∂²/∂y²(∂u/∂x) = ∂³u/∂x∂y²,
∂²ε_y/∂x² = ∂²/∂x²(∂v/∂y) = ∂³v/∂x²∂y
∂γ_xy/∂x∂y = ∂²/∂x∂y(∂v/∂x + ∂u/∂y) = ∂³v/∂x²∂y + ∂³u/∂x∂y² //

Ex. 2. 2(∂²ε_x/∂y∂z) = ∂/∂x(–∂γ_yz/∂x + ∂γ_zx/∂y + ∂γ_xy/∂z)

∂²ε_x/∂y∂z = ∂/∂y∂z(∂u/∂x) = ∂³u/∂x∂y∂z
∂γ_yz∂x = ∂/∂x(∂w/∂y + ∂v/∂z) = ∂²w/∂x∂y + ∂²v/∂x∂z
∂γ_xy/∂z = ∂/∂z(∂v/∂x + ∂u/∂y) = ∂²v/∂x∂z + ∂²u/∂y∂z
–∂γ_yz/∂x + ∂γ_zx/∂y + ∂γ_xy/∂z = 2(∂²u/∂y∂z) //

Def. 体積歪, ε_vol = lim_V→0(ΔV/V), V: 元の体積, ΔV: 体積変化

垂直歪 ε_x, ε_y, ε_zは体積変化伴う ↔
剪断歪 γ_xy, γ_yz, γ_zxは体積変化伴わない
→ ε_vol = (1 + ε_x)(1 + ε_y)(1 + ε_z) (2次以上の微小項無視)

主歪: 互いに直交する3つの方向

→ 剪断歪 = 0 ⊥ 鉛直歪 = 極大値(か極小値)
→ その時の歪 e₁, e₂, e₃ ≡ 主歪

応力と歪の関係

応力 = 内力の力の釣り合い ⇔ 歪 = 変形の幾何学 → 両者の関係
弾性論: 等方性･均質性を仮定し、フックの法則を基礎

等方性: 方向によってその力学的特性が同じ(↔ 異方性)
均質性: 場所によってその力学的特性が同じ(↔ 不均質性)

一般化したフックの法則

同じ方向の垂直歪と垂直応力は比例
鉛直応力により、それと直交する鉛直歪も変化(符号反対)
同じ方向の剪断応力と剪断応力は比例

ヤング率 Young's modulus, E (N/m²): 歪と単位断面積Sあたりの応力との比例定数(応力と同じ次元)

物質により決まる量。試料の形・大きさによらない
ε_x = σ_x/E (E ヤング率)
ε_y = –vε_x = –v·σ_x/E = –σ_x/(mE) (v ポアソン比, m ポアソン数 – 無次元)
ε_z = –vε_x = –v·σ_x/E = –σ_x/(mE)

垂直応力 → 同じ方向の垂直ひずみは1/Eに比例し変化
引張応力に対し同方向の垂直歪 = 引張

↔ 圧縮応力に対し同方向の垂直歪 = 圧縮

引張応力に対し直交方向の垂直歪 = 圧縮

↔ 圧縮応力に対し直交方向の垂直歪 = 引張

垂直応力に対し直交方向の垂直歪と同方向の垂直歪の比 = ポアソン比

同様に
σ_y → ε_y = σ_y/E, ε_x = -v·σ_y/E, ε_z = -v·σ_y/E
σz → ε_z = σ_z/E, ε_x = -v·σ_z/E, ε_y = -v·σ_z/E

→ これらの応力による歪の合計 =

全歪(歪むことによって他成分に影響与えない) ≡ 重ね合わせの原理
ε_x = 1/E·{σ_x – v(σ_y + σ_z)}
ε_y = 1/E·{σ_y – v(σ_x + σ_z)}
ε_z = 1/E·{σ_z – v(σ_x + σ_y)}
ε_vol = ε_x + ε_y + ε_z = (1 – 2v)/E·(σ_x + σ_y + σ_z)

剪断応力と剪断歪の関係

γ_xy = 2(1 + v)/E·τ_xy = 1/G·τ_xy (G 剛性率)
γ_yz = 2(1 + v)/E·τ_yz = 1/G·τ_yz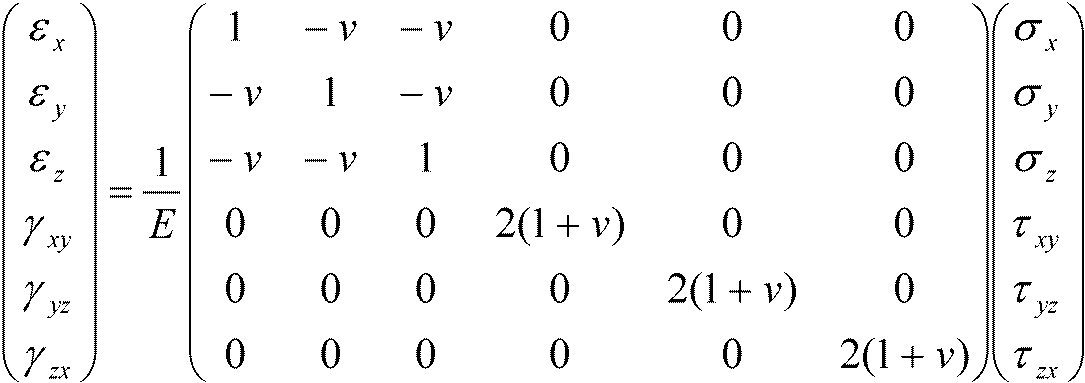
matrix

二次元応力状態

注意: 平面応力状態と平面歪状態の2つがある
1) 平面応力状態: z方向の厚さが極めて薄い平板内応力状態

σ_z = τ_yz = τ_zx = 0
ε_x = 1/E·(σ_x – vσ_y), ε_y = 1/E·(σ_y – vσ_x), ε_z = -1/E·(σ_x + σ_y)
γ_xy = 1/G·τ_xy, γ_yz = γ_zx = 0

2) 平面歪状態: z方向の厚さが十分に厚くz方向に同じ形をしている状態

= z方向に垂直歪生じない
ε_z = γ_yz = γ_zx = 0 → σ_z = v(σ_x + σ_y)
ε_x = 1/E·{σ_x – vσ_y – v²(σ_x + σ_y)} = (1 + v)/E·{(1 – v)σ_x – vσ_y}
ε_y = (1 + v)/E·{(1 – v)σ_y – vσ_x}
γ_xy = 1/G·τ_xy, τ_yz = τ_zx = 0

弾性歪エネルギー, W: 単位体積あたりに蓄えられたエネルギー

→ 1方向からの力(Ex. バネ)により弾性変形により蓄えられるエネルギー
= (荷重・変位)/2
Ex. 長さdx, dy, dzの直方体, σ_xによってε_xに歪
→ 荷重 = σ_xdydx, 変位 = ε_xdx
∴ 直方体に蓄えられたエネルギー = 1/2·σ_xε_xdxdydx → W = 1/2·σ_xε_x

エアリー Airy の応力関数

仮定: 平面応力状態

力の釣り合い式: ∂σ_x/∂x + ∂τ_xy/∂_y = 0, ∂τ_xy/∂x = 0
歪の適合条件式: ∂²ε_x/∂y² + ∂²ε_y/∂_x² = ∂²γ_xy/∂x∂_y
歪と変位の関係式: ε_x = ∂u/∂x, ε_y = ∂v/∂_y, γ_xy = ∂v/∂x + ∂u/∂y
応力と歪の関係式: ε_x = 1/E·(σ_x – vσ_y), ε_y = 1/E·(σ_y – vσ_x),
γ_xy = 2(1 + v)/E·τ_xy

→ σ_x = ∂²F/∂y², σ_y = ∂²F/∂x², τ_xy = ∂²F/∂x∂y とおくと力の釣り合い式を満足
上式と応力とひずみの関係式を歪の適合条件式に代入すると次式を得る

∂⁴F/∂x⁴ + ∂⁴F/∂x²∂y² + ∂⁴F/∂y⁴ = 0
→ 4階微分方程式 (≡ 重調和関数), F ≡ エアリーの応力関数
力学的: 方程式を満足するF → 1-4関係を全て満たす
→ 境界条件、幾何学的条件を満足するよう解けば、応力、歪等の関係得られる

弾性率(係数) (elastic) modulus, modulus of elasticity (N/m²)

剛性率 rididity, G (ずれの弾性率shear modulus): τ = Gθ
体積弾性率 bulk modulus, K: p = -K·ΔV/V

solid
長さ1の立方体 Δν = -νΔa

圧縮率 compressibility, K^-1

E·ν → K, K = P/(-Δν/V)

1) 1.1'面にpの圧力を加える

Δν = -Δb/Δa = 0, Δa = P/E, P = E·Δa/a
Δa, -νΔa

2) 2.2'面に更にpの圧力を加える

E = (1 – νΔa)(P/E) = Δa – νΔa² 3) 3.3'面の歪みを求めよ

  1
  2
  3

1-1'の長さ
1
1 - Δa
1 - Δa + νΔa
1 - Δa + νΔa + νΔa

2-2'の長さ
1
1 + νΔa
1 + νΔa - Δa
1 + νΔa - Δa + νΔa

3-3'の長さ
1
1+νΔa
1+νΔa + Δa
1 + νΔa + Δa - νΔa

体積
1

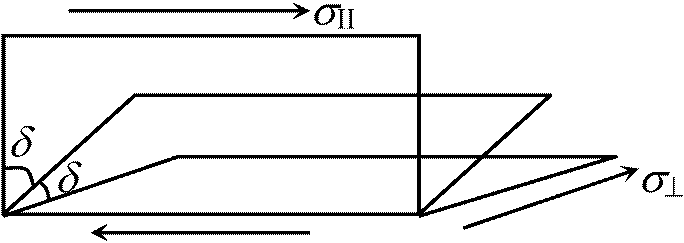
(Δa)²よりも小 → 全て無視
Δν = (-3 + 6ν)Δa

= 3(2ν - 1)Δa
= 3(2ν - 1)·P/E

K = -P/ΔV = E/(3(1 - 2ν)) > 0
ν < 0.5
Eν → G
G = σ_II/δ

E, K, G, νの間の関係を確認せよ

Ex. 1. 薄肉円筒の管壁に働く応力

力の釣り合い equilibrant (force) (or, balanced force)
solid

半径: b, 薄肉 → 外径 ≈ 内径, 内圧: P_i 外圧: P_o

f = ∫₀^pPbsinθdθ = Pb|cosθ|₀^π = b/(b – a)·(P_i – P₀)
b - a « b
αを求める

solid
solid

Ex. 2. 缶詰

ps = pπa²
pπa² = σ'²πa(b - a)

Ex. 3. 針金(棒)のひねり → 歪と応力

N = kθ
k = 1/2·G·πa⁴/l

Ex. 4. δ(E, W, l, a, b)/δ, l, a, bの測定からEを求めることができる

金属学 metallurgy

延性 ductility: (金属の)張力を受け細長く引きのばされる性質
展性 malleability (v. malleable 展性のある): 圧力を加え薄い板状や箔にすることが出来る性質
膨張(伸び) dilation
曲率中心 center of curvature: 曲線(面)の曲がり方の度合を計る時の中心点

流体力学 (fluid dynamics)

気象学、水理学の基礎 → 気体・液体構成する物質全体としての"流れ"を扱う
Def. 流体 fluid: 固有の形がない物質 = 気体 gas + 液体 liquid → 流れ flow
Def₁. 粘性(粘度/粘性率/粘性係数) viscosity, μ or η: 流体の粘り度合 ⇒

流体各点で速度異なる → 内部に摩擦力 → 粘性がある
物質により一定と仮定多(経験的)

単位 = mPa·s(粘度) / mm²/s(動粘度)
Ex. 水 = 1.002/1.004 (20°C), 0.282/0.295 (100°C)

Def₂. 粘性: 分子間引力 → 速度大(小)な分子は負(正)の加速度を受けること

粘性流体: 流速の違う面の間でお互いに力を及ぼす(摩擦の一種)

Ex. 壁の近くでは流速低い

F/S = η·dv/dy,

F: 摩擦力, S: 断面積, dv/dy: 流速勾配

完全流体 perfect fluid: 粘性0の流体 → 流れに平行な面の摩擦0

静止流体: 静止状態(at rest) → 力学的エネルギーに粘性影響、摩擦等を考慮しなくてよい

不完全流体 imperfect fluid (粘性流体 viscous fluid): 粘性のある流体

圧縮 compression

Def. 非圧縮性流体(縮まない流体 incompressible fluid): 流体密度一定
Def. 圧縮性流体(縮む流体 compressbile fluid): 流体密度時間場所で変化

Def. バロトロピー流体: 圧縮性流体中で密度がpのみで決定 → ρ = f(p) (p = 圧力, ρ: 流体密度)
Def. ニュートン流体: 速度勾配du一定な流体(du/dt = constant)

管中に流体があると壁付近では速度0だが壁からの距離に比例し流速が早くなる

Def. 靭性 toughness: 物質の粘り強さを表す技術用語

⇔ 靭性小 = 脆性(もろさ) brittleness

静止流体 (static fluid)

AはBから圧力を受ける(BはAから圧力を受ける) = 境界面に平衡な力ない。境界面に垂直な力のみ

→ 流体に関して常に成立(粘性の有無に無関係)

Def. 圧力 pressure, p: 単位面積あたりに働く力

p = F/S

F: 面に及ぼす力, S: 面の面積

⇒ F = pS
標準単位, N/m²; ≡ Pa (パスカル)

10² Pa = 1 hPa, 10⁶ Pa = 1 MPa (10⁵ Pa = 1 bar バール)

気圧 atm: 1 atm ≈ 10¹³ hPa

→ 1 atm ≡ 76 cmの水銀柱が底面に及ぼす圧力

トル Torr (17 C, トリチェリ, 伊): 非SI系単位

1 Torr = 101325/760 Pa ≈ 水銀柱ミリメートル(実用上同)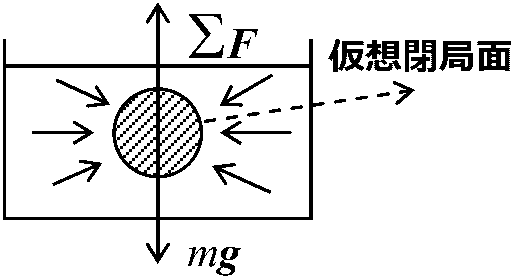
(協定) 水銀柱ミリメートル: g = 980.665 cm/s², 流体 ρ = 13.5951 g/cm³, h = 1 mmに垂直な柱底面圧力

液体静止 → 液体のどの部分でも力は釣合う

Ex. 斜線部分の流体は静止 ∴ΣF + mg = 0, m = Vρ₁m

Def. 浮力 buoyancy (buoyant force), -mg = ΣF = -Vρ₁g (→ 圧力の等方性)

Vρ₁g : 押しのけた液体の重さ
液面: 同じ深さでは同じ圧力 → 液面は同じ高さとなる

アルキメデスの原理 Archimedes' principle

「物体に働く浮力は押しのけた液体の重さに等しい」
Def. 比重 specific gravity, S

4°Cの水(ρ_w)の質量に対する比, S = ρ/ρ_W
⇒ Def. 比重量: ρg Def. 比体積: v = 1/ρ

[応用] 木材体積測定

(空気中の重さ値) - (水に沈めた時の重さ値) = 水中の重さ値

→ 水比重を1 (g/cm³)とみなせば、水中の重さの値は体積と同じ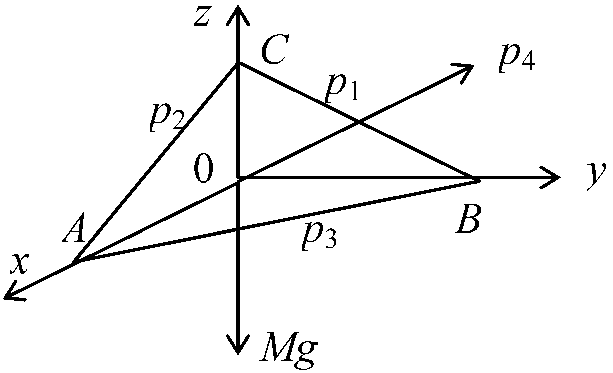

力の釣合い
x成分: ΔBCO × p₁
ΔABCを通して働く
x成分 = p₄ × (ΔABCのx面への射影) = p₄ × ΔBCO
y成分: p₂ = p₄
z成分: p₃ = p₄
ΔABCを原点に近づける → 0 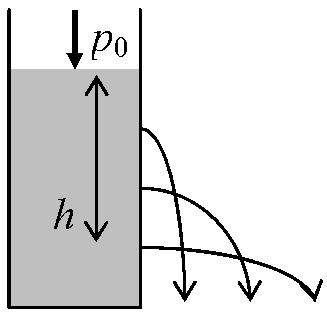fluid

p = ρgh + p₀ → 底の方が圧力高く勢いよく水出る
キャビテーション cavitation: 流動水等の液体圧力が局部的低下 → 蒸気や含有気体を含む泡発生

パスカルの原理 Pascal's principle

(Pascal, Blaise 1623-1662, 仏: 数学・物理・哲学 → 「人間は考える葦である」) 密閉容器内静止流体 → 一部分に受けた圧力を流体内のあらゆる部分に同圧力で伝達する
≡ 平面内の圧力は全て等しい(静止流体の著しい性質)

[応用] 降圧器 step-down transformer ↔ 昇圧器 step-up transformer。水圧プレス hydraulic press

Q. 同径針 → 細い注射器の方が軽い力で注射できる理由(針先液圧は同じ)

表面張力 surface tension

fluid
表面張力

界面 interface
試料物質のE_f = 単位面積に働く力(圧力)を測定し求められる
表面自由エネルギー = その中の単位長さに沿って働く力(表面圧)を測定すれば決定される

全系の内部エネルギー増加
dU = TdS - p^αdV^α - p^βdV^β + γdA + μ^αdN^α + μβdN^β

dA: 界面面積の増分

表面張力, γ = (∂U/∂A)_S, V^α, V^β, N^α, N^β [dyn/cm]

→ 表面ヘルムホルツ自由エネルギー(γ = F^S/A)に等しい

Def. 表面張力(N/m), T = dS/dW

dS: 液体表面積増分 dW: dSに費やした仕事

= 液体表面の縮まろうとする力 → 単位長さあたりに働く力
毛細管現象 (毛管現象, 屏風) capillarity: 毛管内表面張力による負の圧力、水と毛管壁との間の付着力、吸い上げた水の重さのつり合いにより、ある一定の所まで上昇する現象

メニスカス meniscus: 物体間の極小隙間にできる液体架橋

測定法

1) 泡圧法: 不活性気体の泡を作り、泡が破裂に要する圧力を測定
管(T, P = constant)を液体中に浅くつける → 毛細管内気体圧力↓(徐々)

→ 毛細管先端で形成される気泡が半球径になるようにする, その時の力F, 収縮 reduction 力 F_c
F = πR²p … (1) p: 内部-外部圧力差 R: 毛細管先端内径
F_c = 2πRγ … (2)

破裂する瞬間: (1) = (2) → γ = Rp/2 → ρ求まる

Ex. 毛細管(10^-2 cm φ)先を容器(5 cm φ)に入れた液体表面に先端浸し、泡が持ちこたえる最大圧力を不揮発性圧力計の液体密度と高さ(圧力径液体最大高, セカトメータか標準試料参照)hを測定

p = hρg → γ = Rhρg/2

[精密研究] 補正compensation必要。1/1000精度での補正表面張力は γ = (Rhρq/2)(1 - 2Rρ₀/3hρ)

2) 液滴法(滴計測法): 垂直な毛細管の下端から落下する液滴重量

∝ 毛細管の外径と液体表面張力

比例定数: 液滴体積と(v)の立方根に対する毛細管外径(R)の比で表される

mg = 2πRγ·f(R/v^1/3) m: 液滴質量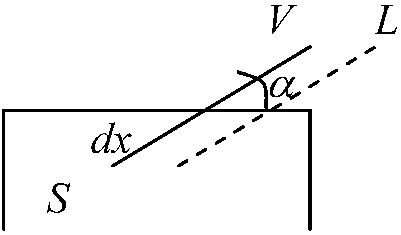

3) 毛細管上昇法
両端開いたガラス毛細管を液中に垂直に立て、液体上昇高と外の高さの差 → 表面張力
S: 2流体LとVと平衡にある固体 (P, T = constant)
α (接触角): L-V界面と固体の平な表面との角

γ_SL, γ_SV, γ_LV: 3界面を含む3つの表面張力

これら3特有定数γ_iにより角α決まる → dG_{T, P, N} = 0から求まる

V-L界面を水平方向にdx変位させると自由エネルギー(dG)変化は

dG = γ_SVdx – γ_SLdx – γ_LVdxcosα = 0
∴ γ_SV = γ_SL + γ_LVcosα … (3)

液体が蒸気と平衡: 内径Rの毛細管中を高さL上昇
→ 液には重力と3表面張力が作用
平衡条件: dG_{T, P} = ΣγdO + Σ(μ + mgL)dN = 0

最初の求和は全界面に渡って、2番目の求和は全ての均一相に含まれるあらゆる分子種について行なう。円筒内の液体高さがdL上昇するとSL界面はそのため2πRdL増加し、SV界面はこれと同じだけ減少する

→ 第1項はΣγdO = (g_SL – g_SV)2πRdLとなる

(μ_L = μ_V, dN_L = –dN_VなのでΣμdN = 0)

最後の求和では、密度ρで体積μR²Lの純流体に含まれる質量mの分子数は

N = πR²Lρ/m, MgLdN = πR²LρgdL

→ 平衡条件は (γ_SL – γ_SV)²πRdL + πR²L(ρ_L – ρ_V)dgL = 0

(3)式から γ_LV = RLg(ρ_L – ρ_V)/2cosα
Ex. 水銀の表面張力: γ (dyn/cm)

= 463.6 + 8.32 × 10^-2T – 3.125 × 10^-4T² (T, 絶対温度)

運動する流体(連続流体/連続体, continuous fluid)

運動記述

1. ラグランジュ (Lagrange): 流体粒子の動きを記述

P(x, y, z)

x = f_x(a, b, c, t) y = f_y(a, b, c, t) z = f_z(a, b, c, t)

a) 流跡 path line: 特定流体の塊が辿った道筋

Ex. 液体中に微小な気体泡発生 → 泡は周囲の液体の流れに従い移動

流跡 (軌跡曲線): ある時刻には泡は1 → 泡の軌跡記録 → 1本の曲線を得る

ある瞬間にはトレーサ tracer は1つしか見えない。その残す足跡は現実には見えず、記録にのみ残る

2. Euler: 「流体場 (流れの場)」

流跡線 trajectory: 流体の可視化 visualization → 流体中に目印(トレーサ) → 目印の軌跡 track をとる

a) 流脈 streak line: 特定の一点を通過した流体のつながり

Ex. 煙突からの煙が描く線 → 「特定の一点」は煙突の先端

path line

b) 流線 stream line: ある瞬間の速度ベクトルを辿っていった線(実際に見ること不可能)
c) 流管 stream tube: 一つの閉曲線の各点を通る流線により囲まれる帯

複数の流線を束ねる → 管形成 = 流管
流管中にある流体は、個々には流線に沿い移動 → 流管からはみ出さない

定常流

時間的に一定な流線で表わせる流れ → 流体の微小部分の運動は流線と一致 ↔ 非定常流
流体の流れを求める → 各点における速度分布を求める = Newton力学で解くこと可能

流脈、流跡、流線は一致 ↔ 非定常流では差が生じる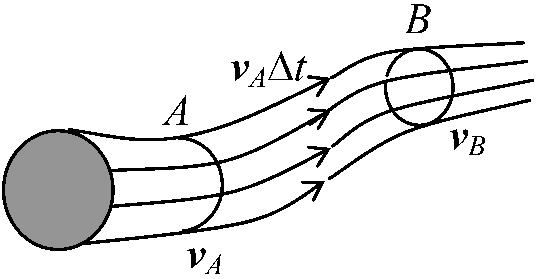

dl = (d_x, d_y, d_z) → dx/v_x = dy/v_y = dz/v_z
→ 連続の式 equation of continuity (定常流)

ρ_Av_AS_A = ρ_Bv_BS_B
(Pr. ρ_Av_AΔtS_A = ρ_Bv_BΔtS_B)
密度一定 → s_Av_A = s_Bv_B
流管: AB間に流体の引き出しなければAから単位時間に流れ込む流体

静圧 static pressure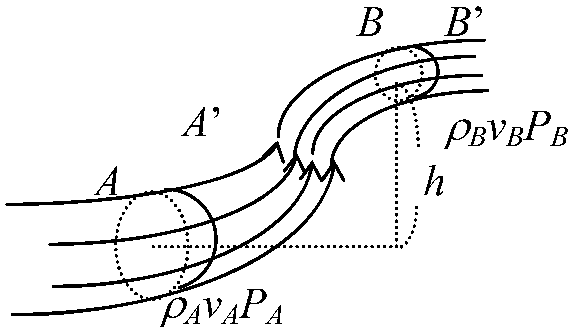
動圧 dynamic pressure
縮まない流体であれば ρ_A = ρ_B ∴ vρ_ASρ_A = vρ_BSρ_B

Th. ベルヌーイの定理 Bernoulli's principle
path line

定常流に関する定理(但し、縮む流体、縮まない流体どちらでも成立)

完全流体(粘性なし) → 速さと圧力の関係式 → 1/2·v² + P/ρ + gh = constant

力 = 圧力差 → 早い[遅い]場所 = 圧力大[小]

Law. 定常流のエネルギー保存則
エネルギー変化: t = 0で仮想的に切り取った流管AB部分(Δ): t = Δt

E(BB') = 1/2·M_BB'v_B² + gM_BB'h
E(AA') = 1/2·M_AA'vA² + 0
E(BB') - E(AA') = (1/2·M_BB'v_B² + gM_BB'h) - (1/2·M_AA'vA²)
Dに外からなされる仕事 = 圧力による
W = ρ_AS_Av_AΔt - ρ_BS_Bv_BΔt (完全流体)
M_AA' = ρ_AS_Av_AΔt, M_BB' = ρ_BS_Bv_BΔt
1/2·ρ_BS_BΔtv_B² - 1/2·ρ_AS_AΔtv_A² + gρ_BS_BΔth

= (P_A/ρ_A)P_AS_Av_AΔt - (P_B/ρ_B)P_BS_Bv_BΔt

連続の式 ρsv = constant
∴ 1/2·v_B² - 1/2middot;v_A² + gh = P_A/ρ_A - P_B/ρ_B (gh = gh_B - gh_A)
1/2·v_B² + P_B/ρ_B + gh_B = 1/2·v_A2 + P_A/ρ_A + gh_A = constant

縮まない流体: ρ = constant ∴ 1/2·v² + P + gρh = constant

Ex. 野球で投げるカーブトリチェリの定理ピトー管 pitot tube

1/2·ρv₀² + P₀ + gρh = 1/2·ρv² + P₀ → 1/2·ρv₀² ≪ ε, v = √(2gh)

定常流の運動量・管壁の受ける力 = Newton運動方程式 → dp/dt = F

Δp = FΔt (力積), h = constant, t = 0 → Δt
Δp = p(BB') – p(AA') = M_BB_'v_B – M_AA_'v_A

= Δρ_BS_Bv_BΔtv_B – ρ_AS_Av_AΔtv_A = ρSvΔt(v_B – v_A)

F = Δp/Δt = ρSv(v_B – v_A) → AB間の流体に働く合力
ポアズイユの流れ

Def. 移流: 大気・海洋において物質・物理量が流速(風)で運ばれる過程

Ex. 温度移流 thermal advection

≡ 速度 × 傾度

移流: 同一地点における物質・物理量変化
輸送: 2地点間の物質・物理量の運搬 →

Def. 流束 flux: 単位時間に単位面積を通過する物理量
回転する流体(回転流体) → コリオリ力

Def. 回転速度 = 回転軸を中心とした回転速度
Def. 回転マッハ数: 回転流体における流れ

= (回転流体絶対速度)/(流体中を伝播する音速)

層流 laminar flow vs 乱流 turbulent flow

層流: 粘性なく乱れ(渦)のない定常流 = 流体中に渦のない一様な流れ

2つの接する流水の速度差小 → 互いの流れを乱しあうことなく流れる

乱流: 多くの渦が上下左右前後に乱れる流れ Ex. 殆どの風

= 属流状態を保てなくなり不規則に流れること
乱流 ⇒ 渦状の運動エネルギー増し圧力減少する
渦動拡散 diffusivity: 乱流渦による拡散 - 大気汚染の主原因

Reynolds, Osborne (1842-1912)
Def. レイノルズ数 Reynolds number, Re: 慣性力と粘性力の比 (∴ 無次元)

Re = ρ·v·r·v_r (v_r ≡ 粘性率)

粘性流体の流れを特徴付ける Ex. 水, R_e > 1000 → 乱流発生

Re小 → 粘性抵抗 > 慣性抵抗, and vice versa

Law. ハーゲン・ポアズイユの法則: 粘性と流量の関係

Q = (πr⁴Δp)/(8ηl),

Q: 単位時間の流量, r: 管半径, l: 管長

空気力学 aerodynamics

気体における流体力学 (空気抵抗 air resistance ⊂ 粘性抵抗)
風の出力 wind power: 風車 windmill → 風力タービン wind turbine

ウィンドファーム wind farm
揚力 lift: 飛行中の航空機を空中に支える力(垂直上向き) → 浮力

[ 砂防 ]

渓流水理

1) 静水圧 hydrostatic pressure: 静止状態での水の圧力
[応用] 水圧 (P, Pa) → 水深 (h, m)

P = ρgh + P₀ ⇒ h = (P - P₀)/(ρg)

ρ: 水密度 (kg/m³, ≈ 1000 kg/m³) - 温度で変化
g: 重力加速度 (≈ 9.81 m/s²)
P₀: 大気圧 (標準大気圧 = 101325 Pa)

Ex. 水圧 = 250,000 Pa、大気圧 = 101325 Pa ⇒

h = (250000 - 101325)/(1000 × 9.81) ≈ 15.15 m

水面下(z)の深さでの静水圧(P): P = w·z (w: 水単位重量, 1 g/cm³ = 1 t/m³)
2) 粘性抵抗 viscosity resistance, τ = μ·du/dz

τ: 剪断変形に抵抗力(= 粘性)
μ = 0.1794(1 + 0.03702T + 0.0001638T²) (T: 摂氏0-100°の場合)
乱流の剪断抵抗力 (τ): τ = r(v + e)(dv/dz)
[ε = l²|dv/dx| » 0 過動粘性係数]

3) ベルヌーイの定理: 仮定 = 非圧縮性、粘性のない流体
≡ 管内に水が流れている時には、圧力水頭pressure headと速度水頭velocity headの和はどの断面でも流れがない時の静水圧にの水頭に等しい
圧力水頭(hp) = p/w
速度水頭(hv) = v²/(2g)
→ 粘性を考慮したベルヌーイ式

v₁²/2g + z₁¹ + p₁/w = v₂²/2g + z₂² + p²/w + ∫_l(l/R)·(v²/2g)dl, or

∫_l(l/R)·(v²/2g)dl: 粘性抵抗によって失われるエネルギー

d/dz(v²/dl) + d/dl(z + p/w) + v²/c²R = 0, c² = l/2g

4) 水流分類
定流 steady flow: 時間的に流れの変化しないもの
等流 uniform flow: 定流のうちで流水断面および勾配が一様なもの

Q = vA = constant, A = constant, v = constant

不等流 non-uniform flow: 等流以外のもの全て

Q = vA = constant, or dQ/dx = 0
I = d(v²/2g)/dx + v²/c²R (ベルヌーイの定理)

不定流 unsteady flow: 時間的に変化するもの

∂A/∂t + ∂(vA)/∂x = 0
I = ∂(v²/2g)∂x + (1/g)∂v/2t + v²/c²R

洗掘 scour ≡ 動いている流体の作用で境界材料が移動し断面拡大すること

河床勾配: 河床の傾斜 → 日本 = 一般に河口から上流に向い上昇
安定勾配(I_b): 土砂で構成されている河床が洗掘も受けず体積も起こらない状態にあるときの勾配

I_b = U_*c²/gR
I_b = {(α/ρ - 1)⁴·d²·q²/(100g²R)}^1/5

5) 局所洗掘: ダム下流部の洗掘等

堰 weir

1) オリフィス orifice: 流量測定を目的とした水槽の壁に設けた孔

オリフィスから流出する流れ: h = (u^P)²/2g = u²/2g

h: 孔の中心から計った水面の高さ
uP: 水槽内での流速 u: 流出水の平均流速

Th. Torricelli(トリチェリー)の定理

上式で(u^P/u)² = (a/A)²を無視 → u = √(2gh)
流量, Q = Ca√(2gh)

c: オリフィスの流量係数 = 0.60-0.65

Q' = C'∫_h₁^h₂{b_z√(2gz)}dz

2) 堰weir: 流れを横断し壁を作り、その上を水が越流するもの

堰は断面の大きい孔の上端が水面と同じ高さにある場合とし取扱える

開水路

平均流速を求める方法