(2025年5月30日更新) [ 日本語 | English ]
HOME > 講義・実習・演習一覧 / 研究概要 > 小辞典 > 個体群
個体群 population, noun古いメモで重要でもないがpopulationの訳が分野により異なることは注意Populatio (L.) 語源 = people (Webster's 20th Century Dictionary)
統計学的関数で表現される特性 → 個体群特有のもので、その集合体内の個体がもつ特徴ではない
Ex. 集合行動 aggregation behavior, 交尾行動 mating behavior 個体群: さらにその生態に直接関係する遺伝的特徴 population genetics → 適応性adaptation、(ダーウィン流)繁殖適応度reproductive fitness、種維持persistence (Odum 1971) 異種個体群: 2種以上の集まり Ex. タンポポ集団、モンシロチョウ個体群表. 時間・空間の対応による個体群規定 時間 短 → 長
生活史中のある令期 1生活環 数-数10世代 地史的年代
空 ある行動の遂行され |行動に規定さ|
間 る生息場所内区画 |れた個体群 |
|生殖場所の個体群: |
狭 生息場所 |個体群生態学研究対象|
↓ |となるディーム |
広 多生息場所含む地理 [地域個体群]
的に区画された地域 | |
-亜種分布区域 |亜種個体群|
種分布区域 |種個体群|
|
[ 分散・分布 ] [ 個体 | 群集 | 環境 | 生態系 ] 亜種個体群 subspecies population: 同種だが環境条件等で変化した集団 地域個体群 local population 生息場所単位個体群 habital population: 種存続可能最小集団 行動規定個体群 behavioral population 自然個体群 natural population自然個体群認識の困難性 (⇔ 実験個体群)Ex. 誘蛾灯に集まる蛾: (空間的)範囲不明瞭で複数個体群の可能性 Ex. 漁獲統計: 空間限定されない Ex. キャベツ畑: モンシロチョウ個体群ではチョウが畑のどこにやってくるかは任意と考えられる
☒☒☒☒☒☒ __〇______〇⇔〇 ___〇⇔〇⇔〇__自然集団 ┗━━━━━━━━━━━┛ 種 個体群は自然状態で連続して存在 ↔ 種の分布はまちまち 実験個体群 experimental population: 一定条件下で実験的に作った個体群 |
[生存可能最小個体群 (minimum viable population)]
|
個体数 number of individuals: 密度測定・推定に必須となる変数
全数カウントは困難なこと多 - 様々な推定手法 Def. 個体密度 density, D = 個体数(N)/生活空間(S)
ある特定の時間や空間に存在する個体群の大きさ バイオマス(生体重) = 現存量 standing crop 個体数測定法直接法(全数調査) ≈ 区画法 quadrat method直接計れる場合 → 一定面積区画作り、その中の個体数数える植物、固着動物、土壌動物等、区画への出入りが殆どない集団のみ可能 円筒法 cylinder metho (枠からの逃げ出しを防ぐ) 間接法捕獲法生け捕り罠: 生け捕り時にストレスを与えない工夫必要機械的方法 Ex. 捕虫網(スイーピング sweeping)、吸虫機(suction catcher)、 ドレッジング、篩、乾式ロート法 Berlese funnel or Tullgren funnel 生物的方法 Ex. 誘蛾灯、餌罠、糞・足跡
個人差・罠種類差が捕獲効率に影響 - 違い埋める工夫必要 CPUE ≠ 捕獲効果(率) = 捕獲効率 × 面積当り捕獲努力量 + マーキング法(標識法): 個体識別 - 全数推定等に必要個体標識 individual marking: 各個体を識別する標識 ↑↓ 一部個体標識など中間的な方法 グループ標識 group marking: 全てに同じ標識前提(1) 標識個体は未標識個体と同じ行動をとる
(2) 標識脱落はない(または低脱落率か脱落率推定が可能) 1. 塗料 (油性ペン、スプレー): ラッカー、プラカラー等がよい 2. 餌(ルビジウム標識) 3. 個体標識 a. 色 × 点 b. 穿孔・切除・焼却 c. 足輪・タグ
両生類・魚類: 指・尾・尾鰭の一部を切除(必要なら再生阻害剤塗布) 痕跡大型動物(哺乳類): 足跡・糞は重要情報 - 消失速度分かれば個体数推定可糞塊密度 dF/dt = A - bF (森下・村上 1970) F: 糞塊数, A: (単位時間当たり)加入糞塊数, b: 瞬間消失率 |
F = A/b·(1 - e-bt) A = bF H := 1個体排泄糞塊数, N := 個体数 ⇒ N = A/H = bF/H 補正: F' = 糞塊発見数 ⇒ α = 糞塊発見率 (≤ 1) ⇒ F = F'/α 足跡(痕跡)密度捕獲法・痕跡利点: 比較的低コスト + 広域密度推定可 個体数推定除去法 removal method一定区域で一定方法で動物除去 →採捕個体数減少曲線 →個体数推定
Ex. パンチュー snap trap によるネズミ個体数推定 (標識)再捕獲法 capture-recapture method1894 Petersen: 魚類. 1930 Lincoln: 鳥類閉鎖個体群における標識個体を用いた動く動物個体群 Ex. 小さな沼でオタマジャクシ(幼生) 1000匹捕獲 - 尾一部切り沼に戻す
x: 沼内の幼生全個体数 → 1000/xの確率で尾を切られた標識個体
→ 1000/x = 8/2000 ∴ x = 250000 (匹) 1. 小標本(再捕獲標識個体少) 2. 消失・加入 - これらが起こらないことは極めて稀 3. 標識脱落 ジョリー・セーバー法 Jolly-Seber method1965 Jolly. 1965 Seber: 独立に発表 (FORTRAN)開放個体群に対応 - 再捕獲を反復することで精度を上げる 捕獲毎に異なる標識 - 同一個体に複数標識 ジャクソンの正法・負法 Jackson method開放個体群に対して一度しか放飼や捕獲ができない - JS法不可正法: 一度に多数の標識個体を放す (未標識個体生息数安定な場合) 負法: 数回に分け異なる標識を付けた個体を放し一斉捕獲 + 修正ジャクソン法 REST自動撮影カメラ活用 = 動物の放射赤外線検知し動作(≈ カメラの前通過)
カメラ性能・設置個所等が密度推定に影響 = 幾つかの仮定 = 100 × 独立撮影回数 / 努力量(= 有効動作期間) 密度推定式: 生息密度, d = E(Y)·E(T)/sHa
E(Y):撮影範囲内侵入回数期待値 |
|
= 棲息地、生息地、生育地 (植物: 成(生)育地という訳が多いように思う)
生息域、住み場所、生息場所、生息環境という訳も稀にみる = ハビタット (訳すのが嫌な人はこちらを使う)Def. 生物(生物個体、個体群)の成育する場所や環境の範囲 |
ハビタットフィルタリング habitat filtering環境条件(温度、土壌等)が生物の生息・繁殖に適した種を選別する過程Ex. サボテン: 乾燥環境によるフィルタリング |
|
Def. 個体群が存続するために必要とする最小個体数 決定要因: 成育地状態(量・質)、動態、遺伝的多様性、外部要因(撹乱等) MVP推定に必要な最低項目人口統計的確率: 出生率や死亡率のランダム変動
小個体群ほど変動に対し脆弱
環境的確率: 気候変動・撹乱等の環境のランダム変動 近親交配や遺伝的多様性の低下につながる可能性
環境収容能力: 環境が永続的に収容できる最大個体数 |
有効集団サイズに影響する因子
性比 50/500則 (50/500 rules)提案 (Franklin 1980, Soulé 1980)
50個体: 近交弱勢防ぐため必要な個体数 当然、絶対的な数値ではない |
分散構造 distributional pattern群集内での各種の配置(散らばり方)分布: 大地域 - 気候、土壌等 ⇔ 分散: 小地域 - 種内・種間競争等 
分布様式規則分布 regular distribution: 個体同士が排他的repulsiveに分布ランダム分布 random distribution: 各個体が全く独立して機会的に分布 集中分布 contagious distribution: 個体同士に引き合いattractive分布 個体群空間分布全数調査 = 理想 ↔ 標本調査 = 現実p(r) = NCrprqN - r
N: 総個体数 p(r) = (e-mmr)/r! pが非常に小さくNが非常に大きいとき
m: 小区画S中に見出される個体数の平均値 |
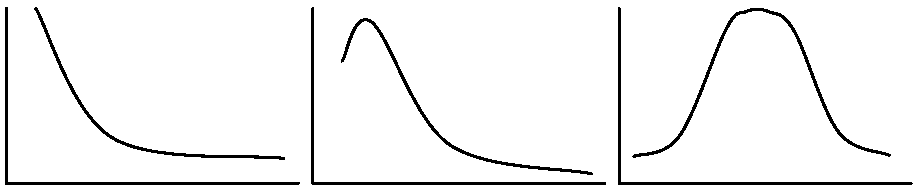 ポアソン分布__________集中分布____________均等分布 Iδ指数 (Morisita's Iδ index), Iδ = qδCase. 個体数: δ = Σi=1qni(n – 1)/{N(N – 1)}
q: 調査区(区画)数 number of stands F0 = {Iδ(N - 1) + q - N}/(q - 1) (F-test) Case. 被度 Iδ(p) = qδ(p) = q·Σi=1qpi2/pavg2 (検定方法は知る限り存在せず)m*-m法(平均込み合い度) (mean crowding)m* = Σi=1qni(ni – 1)/Σi=1qni = Σi=1qni2/Σi=1qni – 1 ⇒m* = m + (σ2/m - 1) ∴ m*/m = 1 + (σ2 - m)/m2 ⇒ m* = α + βm (m: 方形区あたり平均密度) (Iwao 1968)
α: m*軸における切片 &eqiuv; 基本集合度指数
ランダム分布 random distribution
α = 0, β = 1 |
|
1933 Elton 「なぜ何年かに一度、大発生outbreakをする種があるのか」
「大発生は一定間隔でおこるのかランダムなのか」 Ex. 無脊椎海産動物: 気候条件による死亡率。鳥類・哺乳類: 種内要因 調節機構
種内要因: 競争competition、相互干渉mutual interference 食物、生活空間、排出物、伝染病等 個体群変動 fluctuation: 変動を知る方法 - 出生率・死亡率・性比・年齢構成= 個体群とそれを取囲む諸要素の総合化された形: 自然環境下 → 変動幅があり、その枠付けの働きをする過程を"条件付過程 conditioning processes"と呼び、"環境収容力environmental capacity"と密接な関係 生命表 life table (mortality table)ある生物の生殖段階や最高寿命までの生存率を示したもの時間別生命表 time specific life table: ある時間断面での生命表 ある期間の死亡状況が一定であると仮定し、同一時点に出生した仮想集団が年齢とともに死亡により減少していく過程を、死亡率・生存数・平均余命等の生命関数によって表したもの。この仮定のもとでの定常状態の個体群(人口)構造を示す役割も持つコホート(同齢個体群、同時出生集団) cohort: ある特定期間に出生した個体の集まり → 生命表作成の基礎 齢別生命表 age specific life table ≡ コホートの生命表 cohort life table 生存曲線 survival curve生命表をグラフ化したも → 発育に伴う生存個体数減少が視覚的にわかる1974 Deevey. 1958 Bodenheimer: 3型区別
少産・初期死亡低いものは人間や脊椎動物の一部で当てはまる 対数軸 → 死亡率一定なら直線となる
生理的寿命: 理想的条件下生存率 親による子の保護の進化方向
↑ A: 大形哺乳類等 平均寿命 average lifetime: 0歳個体の期待余命 機会的な個体群と平衡的な個体群(Opportunistic and equilibrium populations)r淘汰とK淘汰 (r-selection and K-selection)r淘汰: 個体群成長率や生産力を高める方向に働く = 多産多死 |
K淘汰: 資源利用効率を高める方向に働く = 小産小死
K戦略 (K-strategy) - 安定環境適応型 齢分布 (age distribution)齢構成 age structure: 個体群を発育段階や年齢別区分し数や割合を示す→ 年齢ピラミッド age pyramid
____← 個体数 → 安定齢分布 stable age distributionlx, mxのスケジュールが一定ならば個体群の大きさが増加、安定(固定齢分布)、減少いずれの場合でも結局安定齢分布を示す(Lotka 1922)出生数が毎年同じで、同年に生まれた子供グループが常に同じ生存曲線で成長すれば、齢構成は生存曲線と一致し安定するが、個体群には経年変動があり出生数や死亡要因の種類と強さは毎年異なり、多くの個体群で齢構成は生存曲線とかなり異なる形になる ⇒ 齢構成形から、個体群未来予想可
発展型: 若齢層多いピラミッド型は、若齢個体発育と共に生殖可能個体が増え個体群は成長している 資源抑制 resource control数量生態学 numerical ecologyの手法によって広く研究される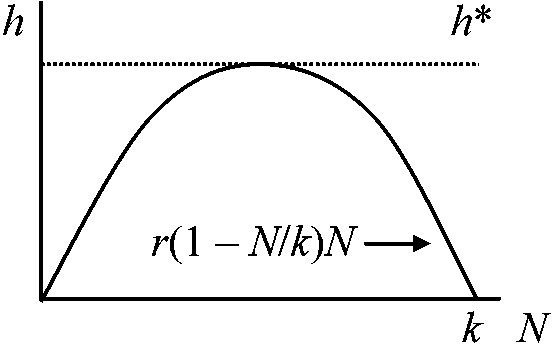 h(t) = constant
h(t) = constantdN/dt = r(1 – N/k)N – h h* > rk/4 → カタストローフ h* =rk/4 h(t), rete of harvesting 実際にはrの求め方が不明
Ex. 漁獲量算定はこの式から導けない 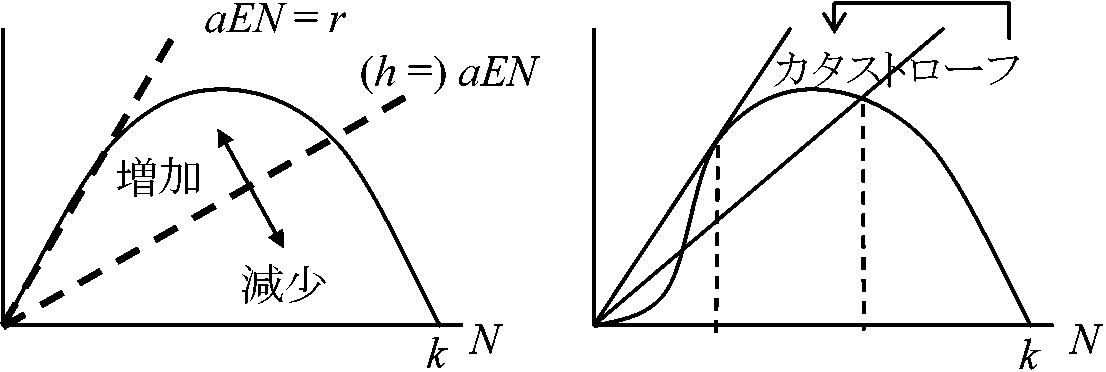
増殖率が小さいとき dN/dt = F(n) – h。ここでh = aEN → カタストロフィックに起こる (Saito et al. 2007) 餌資源と個体群動態x1 = (1 + α1)xt-1 + α2At-1 + εt
x1: t年の個体数 (対数変換値) α1: 密度効果係数 |
純増殖率および増殖価R0: 総繁殖率 net reproductive rate≡ ある平均的な新生個体が一生に生む0齢の子孫の平均個体数1成体♀が次世代に残す成体♀ R0 = Σx=0∞lxmx or R0 = ∫0∞lxmxdx
lx (齢別生存率) < 1: 実数として10000以上欲しい 繁殖価 vx (reproductive value)i) R0 = 0 vx: 将来の子の齢別期待値 ⇒vx = Σt=x∞(lt/lx)·mt or ∫t=x∞(lt/lx)·mtdt ii) R0 ≠ 0 vx: 将来の子の現時点での価値 ⇒
vx/v0 = (ert/lx)Σt=x∞e–rt·lt·mt or (ert/lx)∫x∞e–rt·lt·mtdt vx = mx + Σt=x+1w∞(lt/lx)mt 残存繁殖能力 residual reproductive value, vx* ≡ 右辺2項 vx* = (lx + 1)/lx·vx + 1 → 生残と繁殖のスケジュール: 個体群ごとに異なる (vx curve) 内的自然増加率 intrinsic rate of natural increase ≡ r単位(個体)当たり瞬間増殖率r = b – d (b: 出生率 birth rate, d: 死亡率 death rate) 移入i, 移出eのある場合は r = (b + i) – (d + e)r = 0: 安定個体群サイズ, r > 0: 増加, r < 0: 減少 実験的には Σxe-rxlxmx = 1 (R0 ≈ 1)
r ≈ ln(R0/T), T: 世代時間 - これより導く 密度依存と非依存 density dependence and indepencendeK = r/h h: 一個体存在することにより低下する増加率K: 個体数がこれ以上増加しない個体数(飽和状態) 1953 Haldane: 密度-増殖率関係平衡密度equilibrium density: 個体群が一定密度範囲で変動時の(平均)密度 dN/dt = rN·(K – N)/K = rN - rN2/K 1. 密度非依存要因 density independent factor Ex. 撹乱・天変地異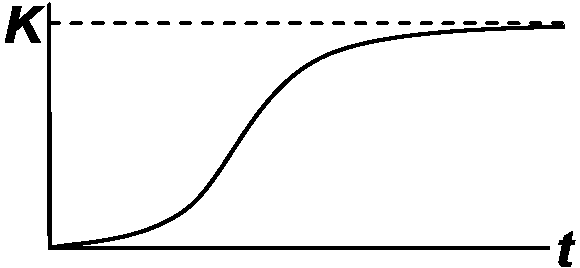 2. 密度依存要因 density dependent factor (ddf)
2. 密度依存要因 density dependent factor (ddf)a. 正の密度依存要因 direct ddf
密度依存要因 (s.s.) – 種内競争、捕食者・寄生者・病原菌
寄生者 ↔ 寄主 捕食者 → 飼種 密度効果 density effectDef. 個体群増殖率に及ぼす密度の影響
相互干渉 mutual interference +
Ex. |_____〇_____| ×2|__〇_____〇__| ×2|_〇_〇_〇_〇_| 1941 Uchida: Callosobruchus chinensisの条件付conditioning実験 種内競争 intraspecific competition 認める
卵 産卵数減少 – 成虫(p)の生理的活性低下
孵化率減少 – 卵死亡 (成虫と衝突、踏付) 幼虫・蛹 孵化虫数 ↔ 幼虫・蛹死亡率
全体ではロジスティック増殖率を示す個体群上でも各密度で要因異なる
Ex. ハバチ・チョウ・ガの幼虫: 集団サイズが小さいと生存できない場合が多く、成長率も下がることがある
死亡率 幼虫期間 蛹体重 集団サイズ小 → "噛み付く"や"喰い付き"できず1, 2齢の死亡率高 Def. 相 phase: 密度・環境変化 → 種の中で異なる形態・行動・生理的状態Def. 相変異 phase transformation (variation) ⊂ 密度効果(集合効果) 他個体が与える刺激量 → 個体群の相決定 刺激(接触刺激が多い)遮断 → 密度効果に関係なくある相示す 実験系(閉鎖環境系): 高密度諸効果 = 負要因に見える ⇔開放系: 産卵数・個体重減少は飛翔能力増す等の正要因 Ex. 移動に有利 Ex. ワタリバッタ等の相転移・集団移動 (種により他の段階的型もある) 密度低 = 孤独相 phase solitaria ⇒ 高 = 群居相 phase gregaria 表. ワタリバッタ相転移 (Krebs 1978)
群居相
孤独相
____________
____
こみあわなさすぎ under-crowding (過疎) 低密度の影響: 閾値現象高密度が常に悪影響を及ぼすとは限らない → 生物個体間の協力的相互作用(アリー効果)密度低すぎると交尾相手が見つかりにくいために繁殖に支障が出ることもある。このような低密度の悪影響が現れているときの個体群動態式として dx/dt = rx(x – a)(1 – x/K) … (1.6) If 0 < a < K → 平衡点 equilibrium point はdt/dt = 0から求まるよう3つ存在
dx/dt = rx(x – a)(1 – x/K) = 0
野外個体群あるいは自然個体群における密度1950年代以降: 密度効果の自然個体群における重要性について激しい論争
論点: logistic curveは自然個体群で成立する? ≡ 密度平衡点存在する? |
1933, 1944 Nicholson: 平衡点有、密度効果重要
個体群平衡は個体群自己制御 self-adjustment, overshooting, and undershooting によってなされる。個体群の生活必須資源(特に食料)が自己制御の主要因
密度依存-密度非依存は明確に分けられる(現在否定)
密度依存(要因)、密度非依存(要因)の区別に意味ない → 密度変化要因は複雑で区別不明確なこと多 自己間引 self-thinning に関する規則仮定: 資源 = 生息空間サイズによる制限 / 個体群(植物や固着性ベントス) = 初期密度高→ 個体成長につれ種内競争↑ → 弱い個体死亡 → 密度↓ Law. -3/2乗則 3/2nd power law自己間引生じる状態での個体群密度D-個体平均重w関係式 ⇒ logw = -3/2·logD + k logw = -α·logD + kk: 定数 → 植物個体群ではα ≈ 3/2が一般的 → -3/2乗則 3/2乗則が成立する生物学的理由光等が成長制限要因 → 植物重量wより植物個体の占める面積(占有面積s)が密度効果に直接的に関与
w ∝ l3, l: 植物体長(樹高・葉長・直径等) → 等成長 isometry
胸高直径断面積合計(A): A = constant 仮定: 利用可能資源量一定 → 全資源を効率的に利用
→ 個体群現存量は密度に関わらず一定 → 密度 ∝-1 (現存量/個体) 昆虫類の個体数変動と種内機構種内密度が競争に関与 = 個体数密度調節に競争が重要な役割
→ 生活必要資源requisite resource供給量が需要量を下回ると密度の自己調節self-regulationを呼ぶ
草食性小哺乳類やその捕食者の周期(規則)的変動 → 要因: 種内機構 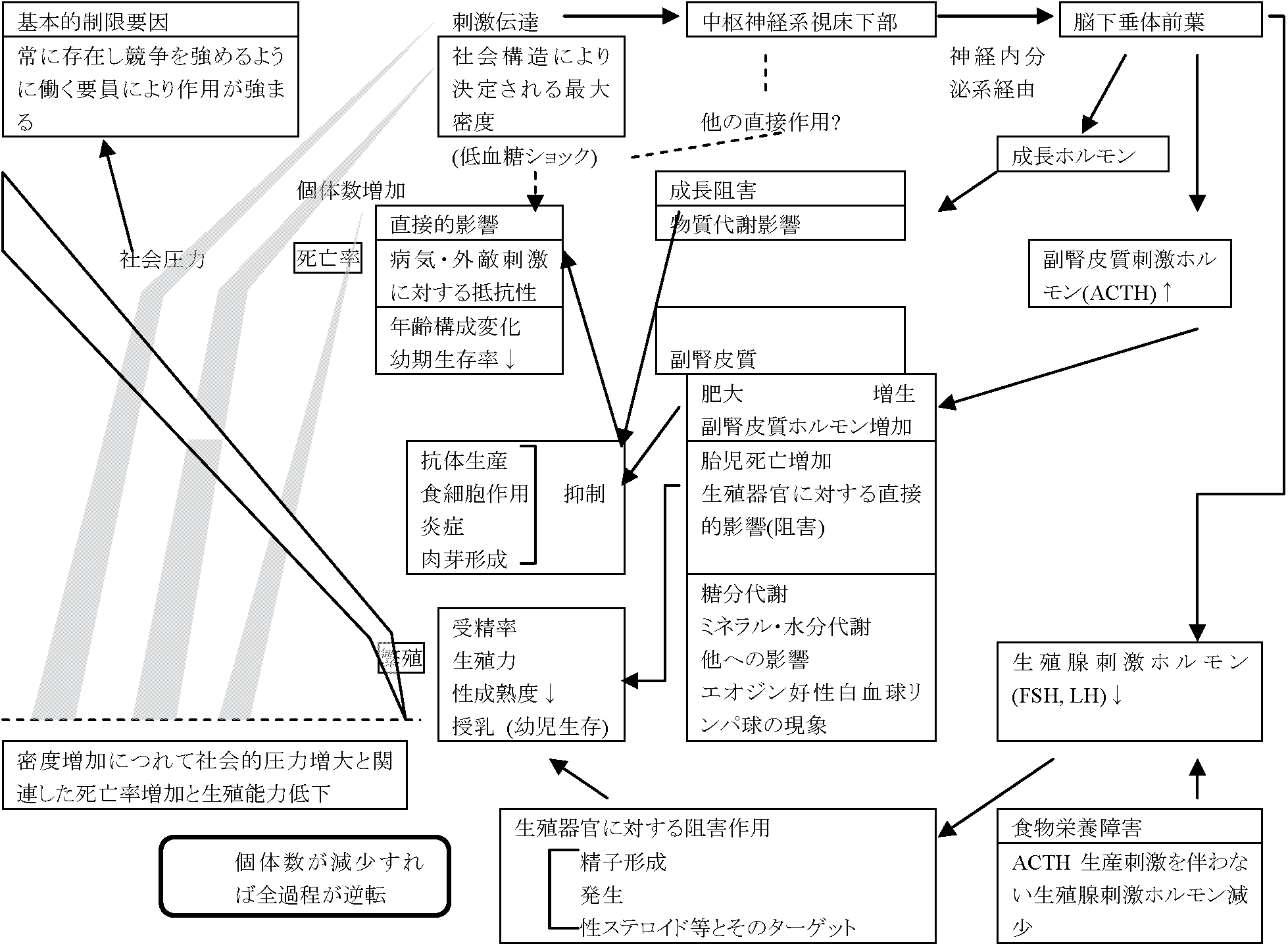
Christian自身、社会心理圧力に対する反応が"脳下垂体-副腎系"という経路のみを通るとは考えていないが、中枢神経系自体のもつより多面的な機能に対する影響が重視されつつある(Myers et al. 1971)
増殖ポテンシャル (Chapman 1928)1. 生存ポテンシャル biotic potential
a) 増殖ポテンシャル reproductive potential → この2つのバランスが個体数の多少を決定 1931 Zwoelfer: N2 = N1e·f/(f + m)·(1 – W/100)
N1, N2: 相続く2世代の個体群密度 平衡種とオポチュニスト種Equilibrium species and opportunistic species (MacArthur 1960)2タイプ: 平衡種 equilibrium species: 時間的に安定
⇔ オポチュニスト種 opportunistic species: 変動を繰り返す
ri = 1/Ni(t)·dNi(t)/dt : 両辺積分 繁殖戦術の進化 (evolution of reproductive tactics)一生の間の繁殖成功度を最大化するように淘汰されてきた
一回繁殖 semelparity Ex. 一年生植物、昆虫、サケ 同一種内産乱数変化: 繁殖開始時期 - 早い繁殖開始 vs 繁殖開始の遅延 死亡率と老齢の進化 evolution of death and aging1975 Medawar: 老衰の進化
1000本の試験管: うち100本を毎月破損し、100本を新しく供給する
A. こわれやすい – 淘汰 有害な遺伝子発現を遅らせることは次世代に悪質な影響を及ぼす 寿命(老衰と死亡)繁殖スケジュールと関係がある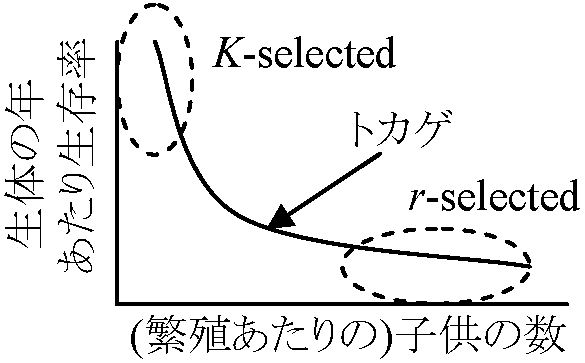
出生率高 → 死亡率高
利点: 捕食されにくい, 物理的環境の影響を受けにくいhigh tolerance * 大型化(定向進化)の利点は不明確(議論中) |
|
Def. 変動量が偶然による期待値より小さい間隔で反復生起する現象
普通は、個体群密度は一定ではなく、季節や年により常に変動 Ex. 一腹子数が多い野ネズミ類個体群密度は、新生個体が現れる繁殖終了期に最大、次の繁殖期前に最低 ⇔ 一腹子数少ない動物や縄張を作る動物は、個体群密度が一年を通じ比較的安定個体群密度経年変動は、主に気候・気象条件変動に誘導される。密度効果により個体群成長を抑制しにくい種や、親による保護が余りなく早死型生存曲線を示す種ほど自然条件の影響受けやすく、個体群密度経年変動も大きくなる。その年の餌や天敵密度も、各生物種の個体群密度に影響し、豊作年・凶作年差が大きい木の実等を主な餌とする動物個体群密度は、しばしば大きな経年変動を示す (真の)周期と疑似周期: 短期間の調査では判断し難い
1916 寺田寅彦: みかけの周期(= 疑似周期) F = 3·(2k(k - 1)(k + 2))/(k + 3)!·Ft
F: 2つの隣合った山の間隔kの頻度 ⇒ これからずれる間隔(周期)は偶然では説明できない 1937 藤原・高橋・増山: 乱数0-9 → 平均変動間隔 = 3 = 周期3 → 周期6, 11に拡張可 (疑似周期で説明できる可能性) 1951 Cole: 藤原らの結論を独立に発見 - Ecologyに報告 ⇒ 偶然変動 = 非周期的変動 vs 非偶然変動 = 非周期的変動 + 周期的変動Ex. 3.5-4年周期: ハタネズミ/タビネズミ + 捕食者 ⇒ 偶然変動も適応可 要因仮説1. ストレス説 (Christian & Davis 1964)病気説: 流行病 → (神経症徴候 ≈ ストレス) → 大発生終息 結果不明確: 複数病原体存在 - 周期性発生困難(病気説否定) ⇒ ストレス説: 個体群サイズピークから急減少の要因 = ストレスEx. ハタネズミ個体群: ストレス症候群 = ショック死 1937 Green & Larsen: 1933 カワリウサギ大発生 → 数年で大減少原因: 非病原性ショック死 - 後に言う適応症候群 1950 Selye H: 1987に適応症候群学説(ストレス学説)研究開始ネズミ: 障害性外因(Ex. 火傷、低温、打撲、感染) → 共通する反応 = 副腎皮質肥大、胸腺萎縮、伊・十二指腸出血性潰瘍 ≡ ストレスに対する適応症候群 1950 Christian JJ: ネズミ類大発生 → 死亡病原様々 - ストレス説で説明可大発生 → (冬-春 = 高密度、餌不足、厳冬) → 高ストレス → 激減 副腎重量 ∝ 密度 / 劣位個体ほど高重量 反論: Rattus, Mus - 副腎肥大 ⇔ Microtus, Lemmus - 肥大見られない 1957 Pitelka AA: Utqiaġvik (旧Barrow, AK)でタビネズミ4年周期大発生個体数増 → 餌(草)不足/天敵増 → 社会ストレス 1957 Frank F: ハタネズミでPitelkaと似た結果1966 Lidicker WZ Jr: CA無人島 - ハツカネズミ大発生
1958 高密度期終(300/acre) - 1959 繁殖完全に失敗 - 1960 絶滅 同時期にハタネズミ個体群増大 → 干渉(含ストレス) → 繁殖不成功 2. 気候説: 周期的な気候変動に個体数変動は一致Ex. ハドソン湾のカワリウサギ(被食者)・オオヤマネコ・アカギツネ(捕食者) 1942 エルトン・ニコルソン: 周期的変動 (黒点数 11.125年周期)
太陽黒点数変化 // オオヤマネコ個体数 → 黒点数影響(50年代まで) ⇒ 否定 ∵ 黒点数周期 ≠ 動物周期多、温帯以北に明確な気候周期なし 3. 食う-食われる仮説 predator-pray hypothesis ☛ Lotka-Volterra式= 食物量制限仮説 捕食者に特定被食者あり → 捕食者-被食者間に一定周期の個体群密度変動
Ex. 実験: オレンジ食コウノシロハダニと捕食者カブリダニの一種を同じ飼育容器に入れる → カブリダニがハダニを食べ尽くし両者共に滅びる ⇔ 容器内にハダニしか入れない避難場所作ると、カブリダニ減少と共にハダニが再び増加し、両者個体群密度は一定のずれを持ち周期的変動 |
1959 伊藤: ノウサギ-オオヤマネコ・アカギツネ間 = 食う-食われる関係
オオヤマネコ: 10年周期(タイガ - 餌カワリウサギ) リス増加に従い相対的に種子量減り、両者間に相関関係 寄生者-宿主: 捕食者-被食者関係と捉えることもあるEx. 1931年: 岡山県。ニカメイガ大発生
寄生ハチの寄生率はニカメイガ大発生と共に上昇し、この上昇に続きニカメイガ個体群密度が激減 タビネズミ → 食料(草) ⇒ 糞 → 植物成長 ∴ 周期に時間ラグ(lag)必要 → 高密度時の糞が分解 → 植物利用し成長 → 植物が食料となるまでタビネズミ個体群サイズ小 → 食料利用し個体群サイズ増す 1959 Southwick: 順位制がある個体群はない個体群より大きなサイズで安定順位制が個体群サイズ(と周期)に関与 1966 Krebs 1966: ハタネズミ実験でこの仮説否定給餌 → 個体群サイズ増に直接つながらない 4. 遺伝的制御仮説 (Gitty 1960, 1967) K淘汰有利: 個体選択(繁殖力小) ↔ r淘汰有利: 個体選択(繁殖力大) 問題(不明): 振幅に付随し色々な現象が起こる ⇔ 現象に付随し振幅が起こる☛ 海洋生態学 水界季節変化に伴う環境変化に伴った変動湖沼は、水量が海に比べ少なく、季節による水温変動がやや著しい。水密度は4°Cで最大で、夏季は水移動発生ぜず、深水層に多い栄養塩類は光量に恵まれ、表水層に少ない。秋季に表層水水温下がり、4°Cに近づくと深層水より重くなり、水移動生じ深水層の栄養塩類が表水層に押し上げられる。その結果、植物プランクトンは急速増殖し、光合成量も増大する。春季は表層水の冷水が温められ深水層の水密度に近づき水の対流が起こりやすくなる Ex. ある湖での植物プランクトンと動物プランクトンの1種(甲殻類)の年変動
異常発生質的異常発生: 特定の発育ステージの大きな変化量的異常発生: 発生量abundanceの異常 (社会的にはこちらのみ指すこと多) 時間パターン
空間パターン(Miyashita 1963)地域同時型 scattered type + 蔓延型 spreading-out type ⇒ 多くは複合型気候条件: 気候条件変化 → 大発生誘発 - 集団移動 mass migration 個体数変動に対する極地気候の影響 |
個体群隔離 → 元の個体群と異なる遺伝子頻度の個体群を形成 (新個体群が小さい場合によく見られる)
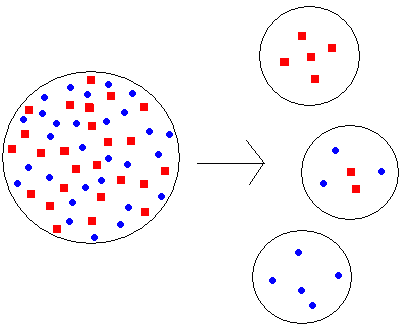
ボトルネック効果(瓶首効果, bottleneck effect)集団の一部分が小集団に分かれたり、急激に減少すると遺伝子頻度は様々なものの入った壜中から偏ったものが飛び出す様に偶然機会で変動 Ex. 火山噴火= 集団個体数激減 → 遺伝的浮動促進 → その子孫繁殖 → 遺伝子頻度が元とは異なる均一性高い(遺伝的多様性低い)集団形成 Ex. Dobzhansky et al. (1957): Drosophilla pseudoobscura
AR/PR – 2遺伝子型 |
Ex. Kerr & Wright (1954): D. melanogaster, ♂4, ♀4 – 96世代
遺伝的浮動: ホモ遺伝子を固定する傾向。ただし、どちらの対立遺伝子を固定するかはランダム
数mileづつ離れてパッチ状に存在。各々の個体群の形質(樹形、樹皮、球果)は、個体群内変異幅は小さいが個体群間変異は大きい 群島効果 island-group effect島が単一でなく群島となる → それぞれの島が隔離島ごとに独自の進化が起きやすくなる Ex. ガラパゴスフィンチ = 単独の海洋島よりも群島の方が多様な進化起こり易い現象 |
|
人口規模・構造・変動を統計分析 + 社会経済・環境等要因との関係 特徴: 人口動態や歴史的変化を研究 (⊃ 人口統計学 demographic statistics: )
人口論 population theory: 人口に関する理論や思想
質(s.s): 人口学的属性により表現された集団の内容あるいは構造 Ex. 年齢、性別、配偶者有無
パレート適性: 他を害さず自己を向上することが不可能になった状態
人口動態 population dynamics人口動態率: 分母集団と分子集団との間に発生関係の存在する比例数
= 人口事象数/人口, データは人口動態統計から
普通(粗)人口動態率 = 人口動態事象数/総人口 特殊発生比例数: 分母人口と分子人口動態上の事象発生人口が同一でないか、ある人口部分集団を分母におきその同一部分集団での発生人口動態事象を分子においた発生比例数
特殊人口動態率(部分人口)
対立比例数: 分母と分子とが異なる統計集団間の関係を表わす 普通構造比例数の特殊化: 普通構造比例数の分母、分子中を分解し特殊構造比例数を導く Ex. 普通有配偶率を男女別や年齢別の特殊有配偶率に分解 特殊構造比例数の総合化: 特殊構造比例数の分母、分子中を分解し普通構造比例数を導く Ex. 合計特殊出生率,総再生産率 年齢構造係数: 総人口に対する何らかの年齢別人口
年少人口係数 = 0-14歳の人口/総人口
年少人口指数 = 0-14歳人口/生産年齢人口 = 老年人口指数/年少人口指数 = 老年人口係数/年少人口係数
平均年齢: 人口に含まれる全員の年齢の平均 |
Def. 人口方程式, Pt = Pt-1 + (dPt-1 – bPt-1) + (i – e) = Pt-1 + Pn + Ps
(ある時点での)総人口 total population, Pt 死亡率 death rate, dPt-1 出生率 birth rate, bPt-1 社会増加 (人口移動 social movement), Ps = i + e 転入数, i 転出数, e (解放生態系 - 推計難しい)
統計的種別人口: 目的により行われる(以下は例)
平均人口: 特定期間(例えば1年間)における人口の平均
労働人口(就労人口) working population, Pw 人口移動分析Nij = a0(Yi/Ni)–a1·(Yj/Nj)–a2 → gravity potential modelNij = a0·(Nia1Nja2/Dija3) D: 距離(移動時間) N: 食糧等の潜在ポテンシャル 流動動分析 (Carruthers 1957): グラフ理論 (Boudeville 1966) - 機能地域電話に基づくグラフ理論による機能地域の決定
重力分析 gravity model
センターへの通話回数
(× 1000回/日)
A B C D E F G H I
センター A 40 20
からの B 10 60
通話回数 C 30 10
D 60 40
E 30 10
F 20 10
G 50 20
H 20 30
I 10 40
|
3観察方法
____↗____↗____↗↑__ 4(齢)
単性分析(性別分析s.s.): Ex. 生命表 Ex. 性比を重みとする加重平均
没性分析: 男女分離しない(できない)ため性別無視し男女総数分析
原子的観察: 個体を観察
アクチュア方式: 経済活動人口調査で調査前特定短期間(Ex. 1週間)における経済活動状態調べる。 Ex. 労働力調査、戦後国勢調査 死亡標準化死亡率 standardized death rate人口規模の違いに死亡率が影響されるので、その地域の死亡状況を全国同様と仮定し、実際の死亡数の程度を全国数値を100とし表したもの。主に小地域間比較に用いる 普通死亡率 crude death rate (粗死亡率)1000人に対する死亡者数(日本: 国勢調査10月1日人口に対する割合) 乳児死亡率 infant death rate1歳未満児死亡者数の同年出生数に対する割合 新生児死亡率 neonatal mortality rate生後4週間未満の乳児死亡の新生児中の割合 周産期死亡率 perinatal mortality rate: 周産期死亡の割合妊娠満22週(154日)以後の死産 + 生後1週未満早期新生児死亡 |
同種・同齢植物個体群(コホート)の密度効果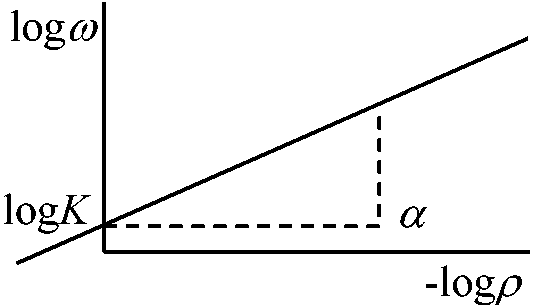 2次元的に配列された植物個体群の相互作用
2次元的に配列された植物個体群の相互作用ρ = N/S … (1) ρ: 個体密度, N: 個体数, S: 面積 y = ωρ … (2)y: 個体群現存量, ω: 平均個体重 ω = ω(ρ, t) – 単純密度効果式 … (3)t: 成育期間 ωρα = K = constant → 経験式(密度効果の巾乗式)Def. α = C-D index (1), (3)より: yρα-1 = K … (4) → tが十分であるとαは1に近づく (3)の両辺のlog: logω = logK – αlogρ (4)およびα = 1とする ⇒ y = K = constant ⇒ Law. 最終収量一定の法則 ρの大きさに無関係にtが十分に大 ⇒ α = 1 ∴ 現存量一定 Def. C-D効果 competition-density effect: 高密度 → 個体重低下= reciprocal equation of competition-density effect (C-D効果) 1/y = B/ρ + A ≡ Y-D効果 (Y-D effect) Def. C-D効果の逆数式: (3)式 ⇒ 1/ω = Aρ + B … (5)
s = 1/ρ (s: 1個体あたりの占有面積) ⇒ f := 成長要因量 ⇒ 1/w = Af + B … (6) or 1/w =A/f + B … (7)
(4) f↑ → w↓ (5) f↓ → w↓
両性要因: 最適値ある要因(線形→逆数要因) Ex. 栄養塩類 C-D効果 + 総収量(個体重 × 個体数) = 一定(飽和) (5)式の誘導仮定(H)H1. ω成長は一般ロジスティック曲線 1/ω·dω/dt = λ(t)(1 – ω/W(t)) or ω = eτ/(∫0t(eτ/W)dτ + K), τ = ∫0tλ(t)dt H2. 成長係数ωは密度ρに関係H3. 最終収量一定の法則 Y(t) = W(t)ρ = constant H4. 初期重ω0が密度ρに無関係に一定 以上4つの仮定よりω - rの関係式として(5)式が導かれる ただし、A = e-τ∫(e-τ/Y)dt, B = e-τ/ω0 個体間の相互作用と個体数の動態均等植えした個体群でも構成個体間の草丈の差が大きくなる (= 相互作用)予測: 草丈の大小の散らばりが相互作用によるものであれば個体間の距離が近いほど相互作用が大きい 時期 t1 → t2にかけての草丈(l)の伸長率(rl)は個体重(wl)を求める rl = (logl2 - logl1)/(t2 - t1) rw = (logw2 - logw1)/(t2 - t1) = Δw = log(w2/w1)/t |